2021-2022学年高二上学期数学人教A版(2019)选择性必修第二册5.3.3函数的极值课件(18张ppt)
文档属性
| 名称 | 2021-2022学年高二上学期数学人教A版(2019)选择性必修第二册5.3.3函数的极值课件(18张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 946.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-30 17:53:25 | ||
图片预览




文档简介
(共18张PPT)
1、了解函数在某点取得极值的条件,掌握极值的定义;
2、掌握求函数极值的步骤和极值的
判定;
3、会用导数求多项式函数的极大值、极小值。
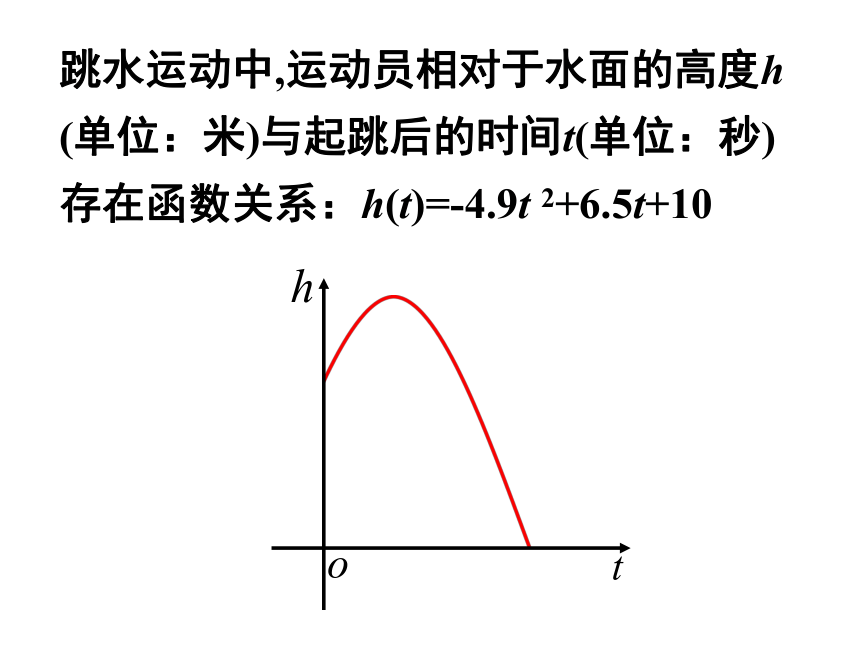
跳水运动中,运动员相对于水面的高度h
(单位:米)与起跳后的时间t(单位:秒)
存在函数关系:h(t)=-4.9t 2+6.5t+10
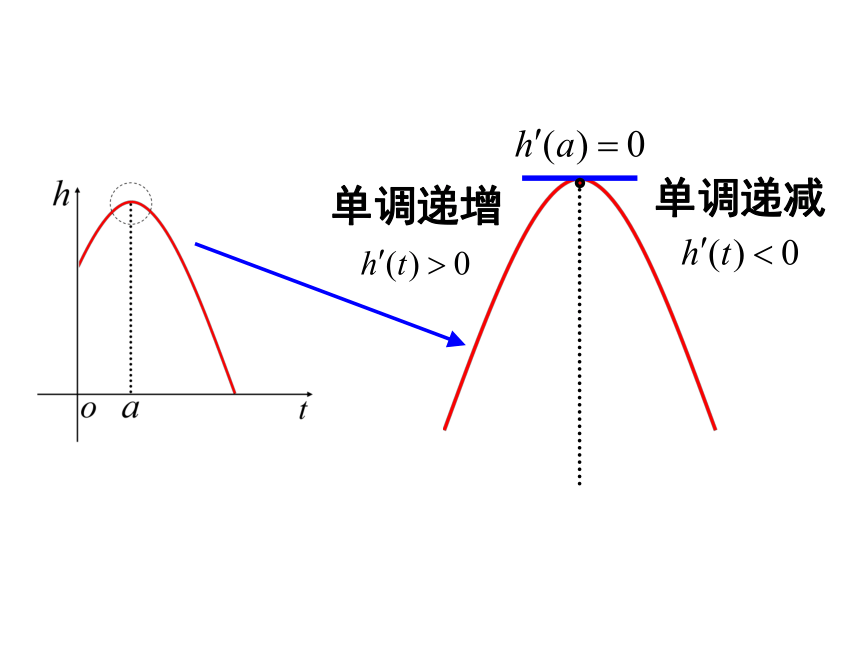
单调递增
单调递减
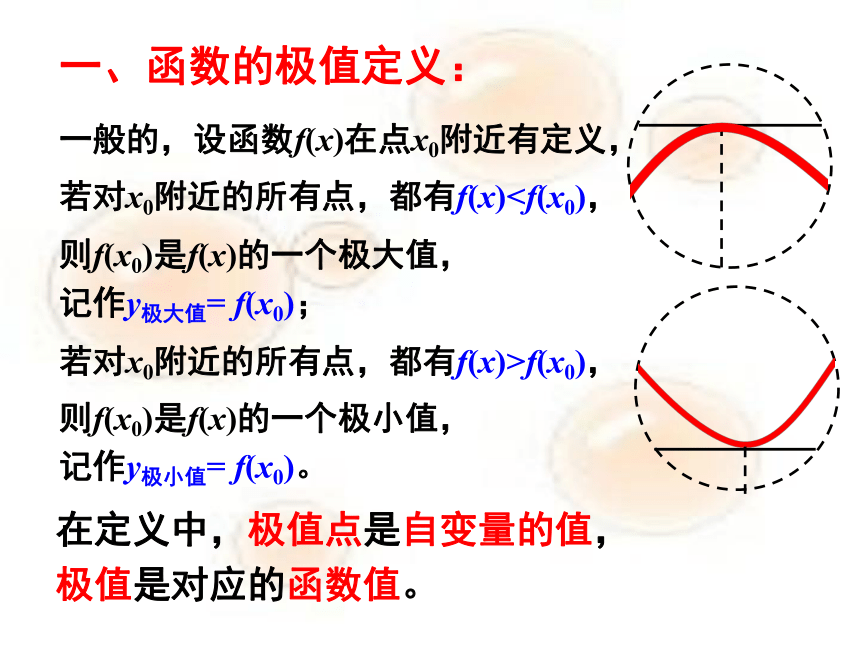
一、函数的极值定义:
一般的,设函数f(x)在点x0附近有定义,
若对x0附近的所有点,都有f(x)则f(x0)是f(x)的一个极大值,
记作y极大值= f(x0);
若对x0附近的所有点,都有f(x)>f(x0),
则f(x0)是f(x)的一个极小值,
记作y极小值= f(x0)。
在定义中,极值点是自变量的值,
极值是对应的函数值。
注意:
(2)函数的极大值与极小值统称为极值。
(3)在定义域内,函数可能有多个极大值或极小值。
(4)函数的极值点一定出现在区间的内部,区间的端点不能成为极值点。而使函数取得最大值、最小值的点可能在区间的内部,也可能在区间的端点。
(1)极大值点、极小值点 统称为极值点。
极大值不一定比极小值大,极小值不一定比极大值小。
y
x
O
问题:观察与思考:极值与导数有何关系?
a
b
y=f(x)
x1
x2
x3
x4
由上图可以看出在函数取得极值处,如果曲线有切线的话,则切线是水平的,从而 。
假设x0使 ,那么在什么情况下,
x0是f(x)的极值点呢?
f (x)<0
y
x
O
x1
a
b
y=f(x)
在极大值点附近
在极小值点附近
f (x)<0
f (x)>0
f (x)>0
x2
二、函数极值的判断方法:
(1):如果在x0附近的左侧 右侧 那么,
f(x0)是极大值;
(2):如果在x0附近的左侧 右侧 那么,
f(x0)是极小值。
练习:下图是 函数 的图象,试找出函数 的极值点,
并指出哪些是极大值点,哪些是极小值点。
a
b
x
y
x1
O
x2
x3
x4
x5
x6
变式:下图是导函数 的图象,试找出函数 的极值点,
并指出哪些是极大值点,哪些是极小值点。
a
b
x
y
x1
O
x2
x3
x4
x5
x6
探索:x =0是否为
函数f(x)=x3的极值点
x
y
O
f (x) x3
若寻找可导函数极值点,
可否只由f (x)=0求得即可
f (x0) =0 x0 是可导函数f(x)的极值点
注意:f /(x0)=0是函数取得极值的必要不充分条件
x (–∞, –2) –2 (–2, 2) 2 ( 2, +∞)
0 0
y
例1:求 的极值。
解:
–
+
+
极大值
极小值
∴当x=-2时, f(x)的极大值为
当x=2时,f(x)的极小值为
总结:求函数f(x)的极值的步骤:
(2)求导数
(3)求方程 的根。
检查 在方程根左右的符号:
(1)确定函数的定义域。
(4)把定义域划分为部分区间,并列成表格
1、左正右负(+ ~ -),取得极大值
2、左负右正(- ~ +),取得极小值
解:(1)
因为f(x)在x=-2,x=1处取得极值
解:(2)
单调增区间为
单调减区间为
【总一总★成竹在胸】
求函数f(x)的极值的步骤:
(2)求导数
(3)求方程 的根。
检查 在方程根左右的符号:
(1)确定函数的定义域。
(4)把定义域划分为部分区间,并列成表格
1、左正右负(+ ~ -),取得极大值
2、左负右正(- ~ +),取得极小值
1、了解函数在某点取得极值的条件,掌握极值的定义;
2、掌握求函数极值的步骤和极值的
判定;
3、会用导数求多项式函数的极大值、极小值。
跳水运动中,运动员相对于水面的高度h
(单位:米)与起跳后的时间t(单位:秒)
存在函数关系:h(t)=-4.9t 2+6.5t+10
单调递增
单调递减
一、函数的极值定义:
一般的,设函数f(x)在点x0附近有定义,
若对x0附近的所有点,都有f(x)
记作y极大值= f(x0);
若对x0附近的所有点,都有f(x)>f(x0),
则f(x0)是f(x)的一个极小值,
记作y极小值= f(x0)。
在定义中,极值点是自变量的值,
极值是对应的函数值。
注意:
(2)函数的极大值与极小值统称为极值。
(3)在定义域内,函数可能有多个极大值或极小值。
(4)函数的极值点一定出现在区间的内部,区间的端点不能成为极值点。而使函数取得最大值、最小值的点可能在区间的内部,也可能在区间的端点。
(1)极大值点、极小值点 统称为极值点。
极大值不一定比极小值大,极小值不一定比极大值小。
y
x
O
问题:观察与思考:极值与导数有何关系?
a
b
y=f(x)
x1
x2
x3
x4
由上图可以看出在函数取得极值处,如果曲线有切线的话,则切线是水平的,从而 。
假设x0使 ,那么在什么情况下,
x0是f(x)的极值点呢?
f (x)<0
y
x
O
x1
a
b
y=f(x)
在极大值点附近
在极小值点附近
f (x)<0
f (x)>0
f (x)>0
x2
二、函数极值的判断方法:
(1):如果在x0附近的左侧 右侧 那么,
f(x0)是极大值;
(2):如果在x0附近的左侧 右侧 那么,
f(x0)是极小值。
练习:下图是 函数 的图象,试找出函数 的极值点,
并指出哪些是极大值点,哪些是极小值点。
a
b
x
y
x1
O
x2
x3
x4
x5
x6
变式:下图是导函数 的图象,试找出函数 的极值点,
并指出哪些是极大值点,哪些是极小值点。
a
b
x
y
x1
O
x2
x3
x4
x5
x6
探索:x =0是否为
函数f(x)=x3的极值点
x
y
O
f (x) x3
若寻找可导函数极值点,
可否只由f (x)=0求得即可
f (x0) =0 x0 是可导函数f(x)的极值点
注意:f /(x0)=0是函数取得极值的必要不充分条件
x (–∞, –2) –2 (–2, 2) 2 ( 2, +∞)
0 0
y
例1:求 的极值。
解:
–
+
+
极大值
极小值
∴当x=-2时, f(x)的极大值为
当x=2时,f(x)的极小值为
总结:求函数f(x)的极值的步骤:
(2)求导数
(3)求方程 的根。
检查 在方程根左右的符号:
(1)确定函数的定义域。
(4)把定义域划分为部分区间,并列成表格
1、左正右负(+ ~ -),取得极大值
2、左负右正(- ~ +),取得极小值
解:(1)
因为f(x)在x=-2,x=1处取得极值
解:(2)
单调增区间为
单调减区间为
【总一总★成竹在胸】
求函数f(x)的极值的步骤:
(2)求导数
(3)求方程 的根。
检查 在方程根左右的符号:
(1)确定函数的定义域。
(4)把定义域划分为部分区间,并列成表格
1、左正右负(+ ~ -),取得极大值
2、左负右正(- ~ +),取得极小值
