2021-2022学年八年级数学苏科版上册《第5章 平面直角坐标系》单元测试卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年八年级数学苏科版上册《第5章 平面直角坐标系》单元测试卷(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 346.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-30 00:00:00 | ||
图片预览




文档简介
《第5章 平面直角坐标系》单元测试卷
一.选择题
1.在平面直角坐标系中,点P(a,b)在第二象限,则点P,(﹣a,b)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.在平面直角坐标系中,点P(﹣2,5)关于y轴的对称点的坐标为( )
A.(﹣5,2) B.(2,5) C.(5,﹣2) D.(﹣2,﹣5)
3.如图,直角坐标系中两点A(0,4),B(1,0),P为线段AB上一动点,作点B关于射线OP的对称点C,则线段AC的最小值为( )
A.3 B.4 C. D.
4.若点B(m+1,3m﹣5)到x轴的距离与到y轴的距离相等,则点B的坐标是( )
A.(4,4)或(2,2)B.(4,4)或(2,﹣2) C.(2,﹣2)D.(4,4)
5.已知点M(3,﹣2),它与点N(x,y)在同一条平行于x轴的直线上,且MN=4,那么点N的坐标是( )
A.(7,﹣2)或(﹣1,﹣2) B.(3,2)或(3,﹣6)
C.(7,2)或(﹣1,﹣6) D.(4,﹣2)或(﹣4,﹣2)
6.在x轴上,且到原点的距离为2的点的坐标是( )
A.(2,0) B.(﹣2,0)
C.(2,0)或(﹣2,0) D.(0,2)
7.如果点P(2,b)和点Q(a,﹣3)关于x轴对称,则a+b的值是( )
A.﹣1 B.1 C.﹣5 D.5
8.已知点(3﹣2k2 , 4k﹣3)在第一象限的角平分线上,则k=( )
A. 1 B. ﹣1 C. 0 D. 0或1
9.如图:下列说法正确的是( )
A. A与D的横坐标相同 B. C与D的纵坐标相同 C. B与C的纵坐标相同 D. B与D的横坐标相同
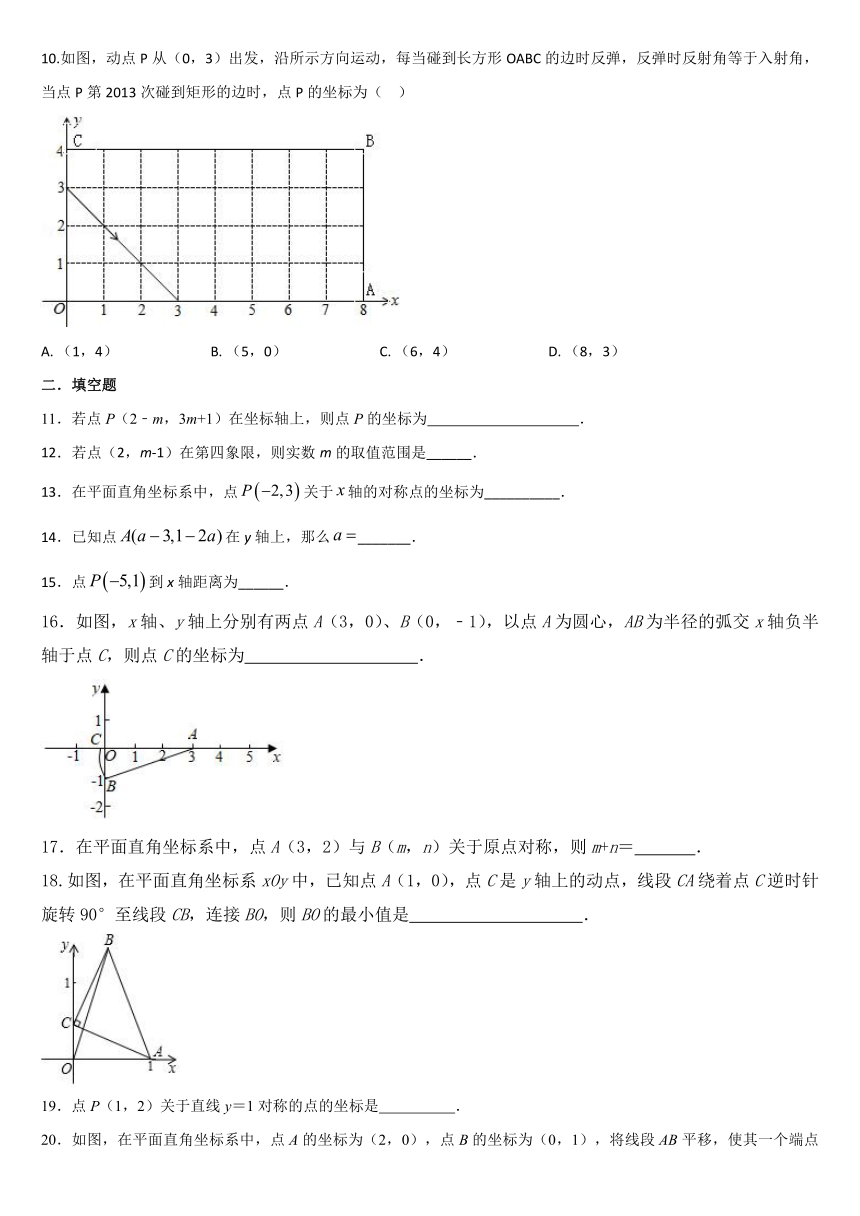
10.如图,动点P从(0,3)出发,沿所示方向运动,每当碰到长方形OABC的边时反弹,反弹时反射角等于入射角,当点P第2013次碰到矩形的边时,点P的坐标为( )
A. (1,4) B. (5,0) C. (6,4) D. (8,3)
二.填空题
11.若点P(2﹣m,3m+1)在坐标轴上,则点P的坐标为 .
12.若点(2,m-1)在第四象限,则实数m的取值范围是______.
13.在平面直角坐标系中,点关于轴的对称点的坐标为__________.
14.已知点在y轴上,那么_______.
15.点到x轴距离为______.
16.如图,x轴、y轴上分别有两点A(3,0)、B(0,﹣1),以点A为圆心,AB为半径的弧交x轴负半轴于点C,则点C的坐标为 .
17.在平面直角坐标系中,点A(3,2)与B(m,n)关于原点对称,则m+n= .
18.如图,在平面直角坐标系xOy中,已知点A(1,0),点C是y轴上的动点,线段CA绕着点C逆时针旋转90°至线段CB,连接BO,则BO的最小值是 .
19.点P(1,2)关于直线y=1对称的点的坐标是 .
20.如图,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(0,1),将线段AB平移,使其一个端点到C(3,2),则平移后另一端点的坐标为 .
三.解答题
21.【阅读材料】
平面直角坐标系中,点P(x,y)的横坐标x的绝对值表示为|x|,纵坐标y的绝对值表示为|y|,我们把点P(x,y)的横坐标与纵坐标的绝对值之和叫做点P(x,y)的勾股值,记为[P],即[P]=|x|+|y|(其中的“+“是四则运算中的加法),例如点P(1,2)的勾股值[P]=|1|+|2|=3
【解决问题】
(1)求点A(﹣2,4),B(+,﹣)的勾股值[A],[B];
(2)若点M在x轴的上方,其横,纵坐标均为整数,且[M]=3,请直接写出点M的坐标.
22.请你给如图建立平面直角坐标系,使文化宫的坐标为(﹣3,1),超市的坐标为(2,﹣3).
(1)画出坐标轴,并写出火车站、体育场、医院的坐标;
(2)直接写出由超市、文化馆、市场围成的三角形的面积.
23.如图,在四边形OABC中,,,,.
(1)求点A,B,C的坐标;
(2)求梯形OABC的面积.
24.已知平面直角坐标系中有一点.
若点M到x轴的距离为1,请求出点M的坐标.
若点,且轴,请求出点M的坐标.
25.如图,在平面直角坐标系中有一个△ABC.
(1)将△ABC向右平移3个单位得到△A1B1C1,画出△A1B1C1.
(2)写出△A1B1C1,三个顶点的坐标.
26.如图,△ABC在直角坐标系中,
(1)请写出各点的坐标;
(2)若把△ABC向上平移2个单位,再向左平移1个单位得到,在图中画出三角形ABC变化后的位置,写出A′、B′、C′的坐标;
(3)求出△ABC的面积.
27.已知平面直角坐标系中有一点M(m﹣1,2m+3)
(1)当m为何值时,点M到x轴的距离为1?
(2)当m为何值时,点M到y轴的距离为2?
参考答案与试题解析
一.选择题
1.解:∵点P(a,b)在第二象限,
∴a<0,b>0,
∴﹣a>0,b>0,
∵点P(﹣a,b)在第一象限,
故选:A.
2.B.
3.A.
4.B.
5.解:∵点M(3,﹣2),MN∥x轴,
∴点N的纵坐标y=﹣2,
点N在点M的左边时,点N的横坐标为3﹣4=﹣1,
点N在点M的右边时,点N的横坐标为3+4=7,
所以,点N的坐标为(7,﹣2)或(﹣1,﹣2).
故选:A.
6.解:∵点在x轴上,
∴点的纵坐标为0,
∵点到原点的距离为2,
∴点的横坐标为±2,
∴所求的坐标是(2,0)或(﹣2,0),故选C.
7.解:∵点P(2,b)和点Q(a,﹣3)关于x轴对称,
∴a=2,b=3,
则a+b的值是:5.
故选:D.
8.【答案】 A
解:∵点(3-2k2 , 4k-3)在第一象限角平分线上,
∴3-2k2=4k-3,
解得k1=1,k2=-3(不合题意舍去).
故答案为:A
【分析】根据第一象限角平分线上的点的横坐标与纵坐标相等且都为正数列出方程求解即可.
9.【答案】 B
【分析】根据平行于坐标轴的点的坐标的特征依次分析各项即可。
【解答】∵AB∥x轴∥CD
∴A与B的纵坐标相同,C与D的纵坐标相同,
故选B.
【点评】解答本题的关键是熟练掌握平行于X轴的直线上的点的纵坐标相同,平行于Y轴上的点的横坐标相同。
10.【答案】 D
解:如图,
当点P经过6次反弹后动点回到出发点(0,3),当点P第6次碰到矩形的边时,点P的坐标为(0,3);
∵2013÷6=335…3,
∴当点P第2013次碰到矩形的边时为第336个循环组的第3次反弹,点P的坐标为(8,3).
故答案为:D.
【分析】根据反弹时反射角等于入射角作出图形,然后判断出第6次反弹时回到出发点,然后用2013除以6,根据商和余数的情况确定出最后点P的位置和坐标即可.
二.填空题
11.解:若点P在y轴上,则2﹣m=0,
解得m=2,
3m+1=3×2+1=7,
此时,点P(0,7),
若点P在x轴上,则3m+1=0,
解得m=﹣,
2﹣m=2﹣(﹣)=,
此时,点P(,0),
综上所述,点P的坐标为(0,7)或(,0).
故答案为:(0,7)或(,0).
12..
【解析】∵点在第四象限,
∴,解得:.
故答案为.
13.
【解析】根据关于轴的对称点的坐标特征:横坐标不变,纵坐标互为相反数可知,点关于轴的对称点的坐标为.
故答案为:.
14.3
【解析】解:∵点A(a-3,1-2a)在y轴上,
∴a-3=0,
解得:a=3,
故答案为:3.
15.1
【解析】根据到x轴的距离为纵坐标的绝对值,可由的纵坐标1,得到x轴的距离为1.
故答案为1
16.(3﹣,0).
17.﹣5.
18..
19.解:点P(1,2)关于直线y=1对称的点的坐标是(1,0).
20.解:①如图1,当A平移到点C时,
∵C(3,2),A的坐标为(2,0),点B的坐标为(0,1),
∴点A的横坐标增大了1,纵坐标增大了2,
平移后的B坐标为(1,3),
②如图2,当B平移到点C时,
∵C(3,2),A的坐标为(2,0),点B的坐标为(0,1),
∴点B的横坐标增大了3,纵坐标增大2,
∴平移后的A坐标为(5,1),
故答案为:(1,3)或(5,1).
三.解答题
21.解:(1)∵点A(﹣2,4),B(+,﹣),
∴[A]=|﹣2|+|4|=2+4=6,[B]=||+||==2;
(2)∵点M在x轴的上方,其横,纵坐标均为整数,且[M]=3,
∴x=±1时,y=2或x=±2,y=1或x=0时,y=3,
∴点M的坐标为(﹣1,2)、(1,2)、(﹣2,1)、(2,1)、(0,3).
22.解:(1)画坐标轴如图所示,
火车站(0,0),体育场(﹣4,3),医院(﹣2,﹣2);
(2)三角形的面积=7×6﹣×5×4﹣×2×6﹣×2×7,
=42﹣10﹣6﹣7,
=42﹣23,
=19.
23.(1)C(0,8),B(8,8),A(16,0);(2)S梯形OABC=96.
【解析】(1)如图,过点B作于点D.
∵,
∴点C的坐标为,
∵CB//OA,,
∴,BC=OD=8,
∵,OC=8,
∴点B的坐标为.
∵,,
∴是等腰直角三角形,
∴.
∴,
∴点A的坐标为.
(2).
24.(1)(-2,1),(-3,-1);(2)(-3,-1)
【解析】(1)∵点M(m-1,2m+3),点M到x轴的距离为1,
∴,
解得,m=-1或m=-2,
当m=-1时,点M的坐标为(-2,1),
当m=-2时,点M的坐标为(-3,-1);
(2)∵点M(m-1,2m+3),点N(5,-1)且MN// x轴,
∴2m+3=-1,
解得:m=-2,
故点M的坐标为(-3,-1).
25.(1)见解析;(2)A1(1,3),B1(-1,0),C1(2,1).
【解析】解:(1)
(2)∵A(-2,3),B(-4,0),C(-1,1)
∴A1(1,3),B1(-1,0),C1(2,1).
26.(1)A(-2,-2),B (3,1),C(0,2); (2)见解析,A′(-3,0)、B′(2,3),C′(-1,4); (3)7.
【解析】解:观察平面直角坐标系得:(1)A(-2,-2),B (3,1),C(0,2);
(2)△A′B′C′如图所示,
A′(-3,0)、B′(2,3),C′(-1,4);
(3)△ABC的面积=5×4-×2×4-×5×3-×1×3,
=20-4-7.5-1.5,
=20-13,
=7.
故答案为(1)A(-2,-2),B (3,1),C(0,2); (2)见解析,A′(-3,0)、B′(2,3),C′(-1,4); (3)7.
一.选择题
1.在平面直角坐标系中,点P(a,b)在第二象限,则点P,(﹣a,b)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.在平面直角坐标系中,点P(﹣2,5)关于y轴的对称点的坐标为( )
A.(﹣5,2) B.(2,5) C.(5,﹣2) D.(﹣2,﹣5)
3.如图,直角坐标系中两点A(0,4),B(1,0),P为线段AB上一动点,作点B关于射线OP的对称点C,则线段AC的最小值为( )
A.3 B.4 C. D.
4.若点B(m+1,3m﹣5)到x轴的距离与到y轴的距离相等,则点B的坐标是( )
A.(4,4)或(2,2)B.(4,4)或(2,﹣2) C.(2,﹣2)D.(4,4)
5.已知点M(3,﹣2),它与点N(x,y)在同一条平行于x轴的直线上,且MN=4,那么点N的坐标是( )
A.(7,﹣2)或(﹣1,﹣2) B.(3,2)或(3,﹣6)
C.(7,2)或(﹣1,﹣6) D.(4,﹣2)或(﹣4,﹣2)
6.在x轴上,且到原点的距离为2的点的坐标是( )
A.(2,0) B.(﹣2,0)
C.(2,0)或(﹣2,0) D.(0,2)
7.如果点P(2,b)和点Q(a,﹣3)关于x轴对称,则a+b的值是( )
A.﹣1 B.1 C.﹣5 D.5
8.已知点(3﹣2k2 , 4k﹣3)在第一象限的角平分线上,则k=( )
A. 1 B. ﹣1 C. 0 D. 0或1
9.如图:下列说法正确的是( )
A. A与D的横坐标相同 B. C与D的纵坐标相同 C. B与C的纵坐标相同 D. B与D的横坐标相同
10.如图,动点P从(0,3)出发,沿所示方向运动,每当碰到长方形OABC的边时反弹,反弹时反射角等于入射角,当点P第2013次碰到矩形的边时,点P的坐标为( )
A. (1,4) B. (5,0) C. (6,4) D. (8,3)
二.填空题
11.若点P(2﹣m,3m+1)在坐标轴上,则点P的坐标为 .
12.若点(2,m-1)在第四象限,则实数m的取值范围是______.
13.在平面直角坐标系中,点关于轴的对称点的坐标为__________.
14.已知点在y轴上,那么_______.
15.点到x轴距离为______.
16.如图,x轴、y轴上分别有两点A(3,0)、B(0,﹣1),以点A为圆心,AB为半径的弧交x轴负半轴于点C,则点C的坐标为 .
17.在平面直角坐标系中,点A(3,2)与B(m,n)关于原点对称,则m+n= .
18.如图,在平面直角坐标系xOy中,已知点A(1,0),点C是y轴上的动点,线段CA绕着点C逆时针旋转90°至线段CB,连接BO,则BO的最小值是 .
19.点P(1,2)关于直线y=1对称的点的坐标是 .
20.如图,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(0,1),将线段AB平移,使其一个端点到C(3,2),则平移后另一端点的坐标为 .
三.解答题
21.【阅读材料】
平面直角坐标系中,点P(x,y)的横坐标x的绝对值表示为|x|,纵坐标y的绝对值表示为|y|,我们把点P(x,y)的横坐标与纵坐标的绝对值之和叫做点P(x,y)的勾股值,记为[P],即[P]=|x|+|y|(其中的“+“是四则运算中的加法),例如点P(1,2)的勾股值[P]=|1|+|2|=3
【解决问题】
(1)求点A(﹣2,4),B(+,﹣)的勾股值[A],[B];
(2)若点M在x轴的上方,其横,纵坐标均为整数,且[M]=3,请直接写出点M的坐标.
22.请你给如图建立平面直角坐标系,使文化宫的坐标为(﹣3,1),超市的坐标为(2,﹣3).
(1)画出坐标轴,并写出火车站、体育场、医院的坐标;
(2)直接写出由超市、文化馆、市场围成的三角形的面积.
23.如图,在四边形OABC中,,,,.
(1)求点A,B,C的坐标;
(2)求梯形OABC的面积.
24.已知平面直角坐标系中有一点.
若点M到x轴的距离为1,请求出点M的坐标.
若点,且轴,请求出点M的坐标.
25.如图,在平面直角坐标系中有一个△ABC.
(1)将△ABC向右平移3个单位得到△A1B1C1,画出△A1B1C1.
(2)写出△A1B1C1,三个顶点的坐标.
26.如图,△ABC在直角坐标系中,
(1)请写出各点的坐标;
(2)若把△ABC向上平移2个单位,再向左平移1个单位得到,在图中画出三角形ABC变化后的位置,写出A′、B′、C′的坐标;
(3)求出△ABC的面积.
27.已知平面直角坐标系中有一点M(m﹣1,2m+3)
(1)当m为何值时,点M到x轴的距离为1?
(2)当m为何值时,点M到y轴的距离为2?
参考答案与试题解析
一.选择题
1.解:∵点P(a,b)在第二象限,
∴a<0,b>0,
∴﹣a>0,b>0,
∵点P(﹣a,b)在第一象限,
故选:A.
2.B.
3.A.
4.B.
5.解:∵点M(3,﹣2),MN∥x轴,
∴点N的纵坐标y=﹣2,
点N在点M的左边时,点N的横坐标为3﹣4=﹣1,
点N在点M的右边时,点N的横坐标为3+4=7,
所以,点N的坐标为(7,﹣2)或(﹣1,﹣2).
故选:A.
6.解:∵点在x轴上,
∴点的纵坐标为0,
∵点到原点的距离为2,
∴点的横坐标为±2,
∴所求的坐标是(2,0)或(﹣2,0),故选C.
7.解:∵点P(2,b)和点Q(a,﹣3)关于x轴对称,
∴a=2,b=3,
则a+b的值是:5.
故选:D.
8.【答案】 A
解:∵点(3-2k2 , 4k-3)在第一象限角平分线上,
∴3-2k2=4k-3,
解得k1=1,k2=-3(不合题意舍去).
故答案为:A
【分析】根据第一象限角平分线上的点的横坐标与纵坐标相等且都为正数列出方程求解即可.
9.【答案】 B
【分析】根据平行于坐标轴的点的坐标的特征依次分析各项即可。
【解答】∵AB∥x轴∥CD
∴A与B的纵坐标相同,C与D的纵坐标相同,
故选B.
【点评】解答本题的关键是熟练掌握平行于X轴的直线上的点的纵坐标相同,平行于Y轴上的点的横坐标相同。
10.【答案】 D
解:如图,
当点P经过6次反弹后动点回到出发点(0,3),当点P第6次碰到矩形的边时,点P的坐标为(0,3);
∵2013÷6=335…3,
∴当点P第2013次碰到矩形的边时为第336个循环组的第3次反弹,点P的坐标为(8,3).
故答案为:D.
【分析】根据反弹时反射角等于入射角作出图形,然后判断出第6次反弹时回到出发点,然后用2013除以6,根据商和余数的情况确定出最后点P的位置和坐标即可.
二.填空题
11.解:若点P在y轴上,则2﹣m=0,
解得m=2,
3m+1=3×2+1=7,
此时,点P(0,7),
若点P在x轴上,则3m+1=0,
解得m=﹣,
2﹣m=2﹣(﹣)=,
此时,点P(,0),
综上所述,点P的坐标为(0,7)或(,0).
故答案为:(0,7)或(,0).
12..
【解析】∵点在第四象限,
∴,解得:.
故答案为.
13.
【解析】根据关于轴的对称点的坐标特征:横坐标不变,纵坐标互为相反数可知,点关于轴的对称点的坐标为.
故答案为:.
14.3
【解析】解:∵点A(a-3,1-2a)在y轴上,
∴a-3=0,
解得:a=3,
故答案为:3.
15.1
【解析】根据到x轴的距离为纵坐标的绝对值,可由的纵坐标1,得到x轴的距离为1.
故答案为1
16.(3﹣,0).
17.﹣5.
18..
19.解:点P(1,2)关于直线y=1对称的点的坐标是(1,0).
20.解:①如图1,当A平移到点C时,
∵C(3,2),A的坐标为(2,0),点B的坐标为(0,1),
∴点A的横坐标增大了1,纵坐标增大了2,
平移后的B坐标为(1,3),
②如图2,当B平移到点C时,
∵C(3,2),A的坐标为(2,0),点B的坐标为(0,1),
∴点B的横坐标增大了3,纵坐标增大2,
∴平移后的A坐标为(5,1),
故答案为:(1,3)或(5,1).
三.解答题
21.解:(1)∵点A(﹣2,4),B(+,﹣),
∴[A]=|﹣2|+|4|=2+4=6,[B]=||+||==2;
(2)∵点M在x轴的上方,其横,纵坐标均为整数,且[M]=3,
∴x=±1时,y=2或x=±2,y=1或x=0时,y=3,
∴点M的坐标为(﹣1,2)、(1,2)、(﹣2,1)、(2,1)、(0,3).
22.解:(1)画坐标轴如图所示,
火车站(0,0),体育场(﹣4,3),医院(﹣2,﹣2);
(2)三角形的面积=7×6﹣×5×4﹣×2×6﹣×2×7,
=42﹣10﹣6﹣7,
=42﹣23,
=19.
23.(1)C(0,8),B(8,8),A(16,0);(2)S梯形OABC=96.
【解析】(1)如图,过点B作于点D.
∵,
∴点C的坐标为,
∵CB//OA,,
∴,BC=OD=8,
∵,OC=8,
∴点B的坐标为.
∵,,
∴是等腰直角三角形,
∴.
∴,
∴点A的坐标为.
(2).
24.(1)(-2,1),(-3,-1);(2)(-3,-1)
【解析】(1)∵点M(m-1,2m+3),点M到x轴的距离为1,
∴,
解得,m=-1或m=-2,
当m=-1时,点M的坐标为(-2,1),
当m=-2时,点M的坐标为(-3,-1);
(2)∵点M(m-1,2m+3),点N(5,-1)且MN// x轴,
∴2m+3=-1,
解得:m=-2,
故点M的坐标为(-3,-1).
25.(1)见解析;(2)A1(1,3),B1(-1,0),C1(2,1).
【解析】解:(1)
(2)∵A(-2,3),B(-4,0),C(-1,1)
∴A1(1,3),B1(-1,0),C1(2,1).
26.(1)A(-2,-2),B (3,1),C(0,2); (2)见解析,A′(-3,0)、B′(2,3),C′(-1,4); (3)7.
【解析】解:观察平面直角坐标系得:(1)A(-2,-2),B (3,1),C(0,2);
(2)△A′B′C′如图所示,
A′(-3,0)、B′(2,3),C′(-1,4);
(3)△ABC的面积=5×4-×2×4-×5×3-×1×3,
=20-4-7.5-1.5,
=20-13,
=7.
故答案为(1)A(-2,-2),B (3,1),C(0,2); (2)见解析,A′(-3,0)、B′(2,3),C′(-1,4); (3)7.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
