2021-2022学年人教版七年级数学下册7.2.2用坐标表示平移同步训练(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版七年级数学下册7.2.2用坐标表示平移同步训练(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 290.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-30 22:45:29 | ||
图片预览



文档简介
2022年春人教版初中七年级数学下册 同步训练
班级 姓名
第七章 平面直角坐标系
7.2 坐标方法的简单应用
7.2.2 用坐标表示平移
测试时间:20分钟
一、选择题
1.(2021湖南长沙开福青竹湖湘一外国语学校期末)点P(-1,-3)向右平移3个单位,再向上平移5个单位,则所得点的坐标为( )
A.(-4,-2) B.(-4,-8)
C.(2,2) D.(2,-8)
2.将线段AB在坐标系中平移,已知A(-1,2),B(1,1),将线段AB平移后,其两个端点的坐标变为A'(-2,1),B'(0,0),点A的对应点为点A',则它平移的情况是( )
A.向上平移了1个单位长度,向左平移了1个单位长度
B.向下平移了1个单位长度,向左平移了1个单位长度
C.向下平移了1个单位长度,向右平移了1个单位长度
D.向上平移了1个单位长度,向右平移了1个单位长度
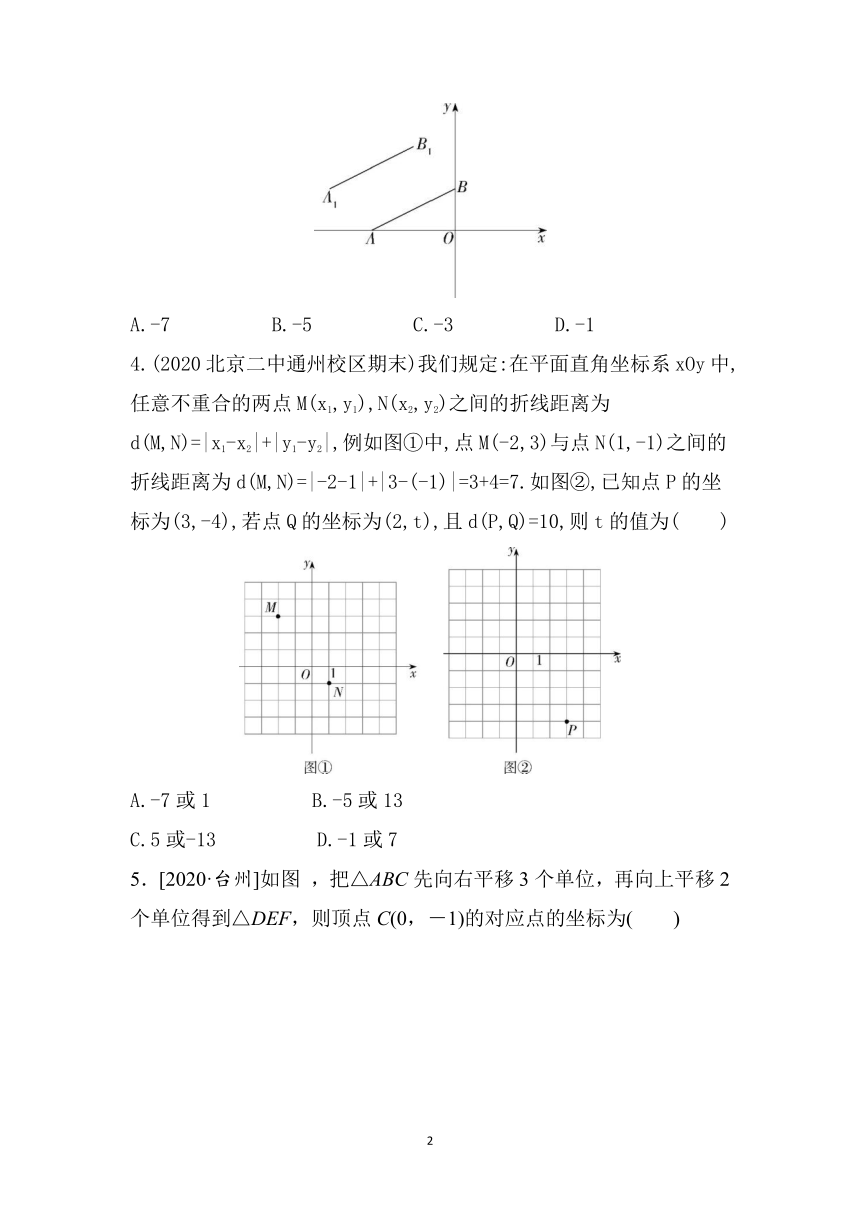
3.(2021宁夏银川兴庆期末)如图,A,B两点的坐标分别为(-2,0),(0,1),将线段AB平移到线段A1B1的位置.若A1(b,1),B1(-1,a),则b-a的值是( )
A.-7 B.-5 C.-3 D.-1
4.(2020北京二中通州校区期末)我们规定:在平面直角坐标系xOy中,任意不重合的两点M(x1,y1),N(x2,y2)之间的折线距离为d(M,N)=|x1-x2|+|y1-y2|,例如图①中,点M(-2,3)与点N(1,-1)之间的折线距离为d(M,N)=|-2-1|+|3-(-1)|=3+4=7.如图②,已知点P的坐标为(3,-4),若点Q的坐标为(2,t),且d(P,Q)=10,则t的值为( )
A.-7或1 B.-5或13
C.5或-13 D.-1或7
5.[2020·台州]如图 ,把△ABC先向右平移3个单位,再向上平移2个单位得到△DEF,则顶点C(0,-1)的对应点的坐标为( )
A.(0,0)
B.(1,2)
C.(1,3)
D.(3,1)
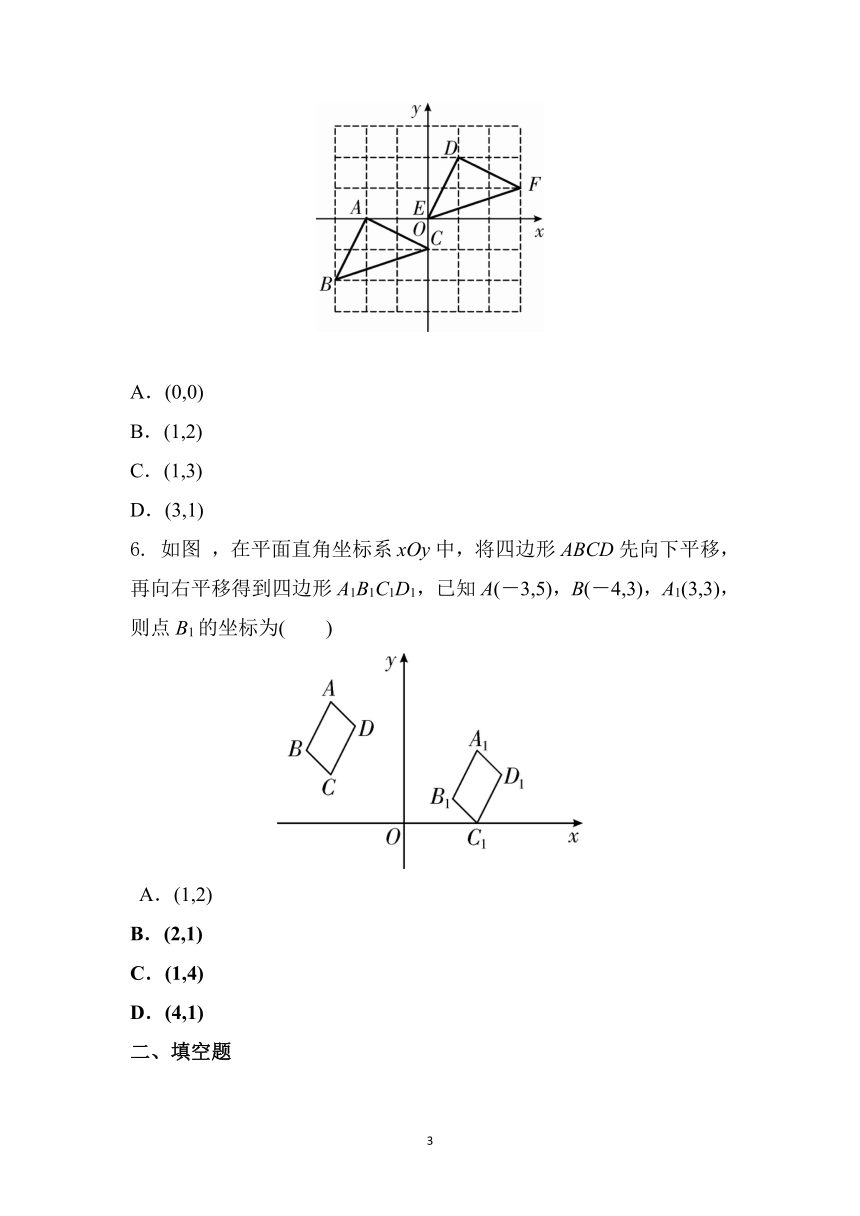
6. 如图 ,在平面直角坐标系xOy中,将四边形ABCD先向下平移,再向右平移得到四边形A1B1C1D1,已知A(-3,5),B(-4,3),A1(3,3),则点B1的坐标为( )
A.(1,2)
B.(2,1)
C.(1,4)
D.(4,1)
二、填空题
7.(2021河北唐山滦州期末)把点A(3,1)向左平移2个单位,再向下平移3个单位后与点B重合,则点B的坐标是 .
8.(2021湖北武汉黄陂期末)在平面直角坐标系中,线段AB经过平移后得到线段CD,已知点A(-3,2)的对应点为C(1,-2).若点B的对应点为D(0,1),则点B的坐标为 .
9.如图,点A、B的坐标分别为(1,2)、(4,0),将△AOB沿x轴向右平移,得到△CDE,已知DB=1,则点C的坐标为 .
10.(2020广西百色二模)三角形ABC中任意一点P(x0,y0)经平移后的对应点为P1(x0+5,y0+3),将三角形ABC作同样的平移得到三角形A1B1C1,若A(-2,3),则点A的对应点A1的坐标为 .
11. 已知△A′B′C′是△ABC经过平移得到的,它们各顶点在平面直角坐标系中的坐标如下表所示:
△ABC A(a,0) B(3,0) C(5,5)
△A′B′C′ A′(4,2) B′(7,b) C′(c,7)
(1)观察并写出表中各对应点坐标的变化;
(2)确定a=________,b=________,c=________,并在图7 2 19中的平面直角坐标系中画出△ABC,△A′B′C′,并求出△ABC的面积.
三、解答题
12.(2021重庆荣昌初级中学月考)如图,直角坐标系中,三角形ABC的顶点都在格点上,其中,C点坐标为(1,-2).
(1)写出点A、B的坐标:A( , )、B( , );
(2)将三角形ABC先向右平移2个单位长度,再向上平移3个单位长度,得到三角形A1B1C1,请作出平移后的三角形A1B1C1,并直接写出三角形A1B1C1的三个顶点的坐标:A1( , )、B1( , )、C1( , );
(3)求三角形ABC的面积.
13.(2021江苏盐城盐都期末)如图,在边长为1的小正方形网格中,三角形ABC的顶点都在格点上,建立适当的平面直角坐标系xOy,使得点A、B的坐标分别为(2,3)、(3,2).
(1)画出平面直角坐标系;
(2)画出将三角形ABC沿y轴翻折,再向左平移1个单位长度得到的三角形A'B'C';
(3)点P(m,n)是△ABC内部一点,写出点P经过(2)中变换后的对应点P'的坐标: .
14.如图 ,在四边形ABCO中,AB∥OC,BC∥AO,A,C两点的坐标分别为(-,),(-2,0),A,B两点间的距离等于O,C两点间的距离.
(1)点B的坐标为________;
(2)将这个四边形向下平移2个单位长度后得到四边形A′B′C′O′,请你写出平移后四边形A′B′C′O′四个顶点的坐标.
15.(2021广西钦州期末)如图,在平面直角坐标系中,点A,B的坐标分别为(-1,0),(3,0),现同时将点A,B先向上平移2个单位长度,再向右平移1个单位长度,得到A,B的对应点C,D,连接AC,BD,CD,得到四边形ABDC.
(1)写出点C,D的坐标,并求出三角形AOC的面积;
(2)点B左侧的x轴上有一点F,使得三角形DFC的面积是三角形DFB面积的2倍,请求出点F的坐标;
(3)点B右侧的x轴上是否也存在点F',使得三角形DF'C的面积是三角形DF'B面积的2倍 若存在,请直接写出点F'的坐标;若不存在,请说明理由.
一、选择题
1.答案 C 点P(-1,-3)向右平移3个单位,再向上平移5个单位,所得到的点的坐标为(-1+3,-3+5),即(2,2),故选C.
2.答案 B 由点A,B的坐标变化可知线段AB向下平移了1个单位长度,向左平移了1个单位长度.
故选B.
3.答案 B ∵A(-2,0)平移后对应点A1的坐标为(b,1),∴线段AB向上平移了1个单位,
∵B(0,1)平移后对应点B1的坐标为(-1,a),∴线段AB向左平移了1个单位,
∴a=2,b=-3,∴b-a=-5.故选B.
4.答案 C 根据题意,得|3-2|+|-4-t|=10,
解得t=5或t=-13.
故选C.
5. 答案 D
6. 答案 B
二、填空题
7.答案 (1,-2)
解析 因为把点A(3,1)向左平移2个单位,再向下平移3个单位后与点B重合,所以点B的坐标是(3-2,1-3),
即B(1,-2),故答案为(1,-2).
8.答案 (-4,5)
解析 由点A(-3,2)的对应点为C(1,-2)可知,平移后各对应点之间的关系是横坐标加4,纵坐标减4,故点B的横坐标为-4,纵坐标为5,
即点B的坐标为(-4,5),故答案为(-4,5).
9.答案 (4,2)
解析 由已知得OD=3,
∴△AOB沿x轴向右平移了3个单位长度,
∵点A的坐标为(1,2),∴点C的坐标为(4,2).
10.答案 (3,6)
解析 ∵三角形ABC中任意一点P(x0,y0)经平移后的对应点为P1(x0+5,y0+3),
∴坐标平移规律是横坐标加5,纵坐标加3,
∵将三角形ABC作同样的平移得到三角形A1B1C1,A(-2,3),
∴A1的坐标为(-2+5,3+3),即(3,6).
11. (1)由观察,得点A,B,C分别向右平移了4个单位长度,然后向上平移了2个单位长度后分别得到了点A′,B′,C′.
(2)
S△ABC=.
三、解答题
12.解析 (1)A(-1,1),B(-3,-3).
(2)如图,三角形A1B1C1即为所求作.A1(1,4),B1(-1,0),C1(3,1).
(3)三角形ABC的面积=4×4-×2×4-×2×3-×4×1=7.
13.解析 (1)平面直角坐标系如图所示.
(2)如图,三角形A'B'C'即为所求作.
(3)P(m,n)沿y轴翻折,得到点(-m,n),再向左平移1个单位长度得到P'(-m-1,n).
14. (1)(-3,)
(2)A′(-,-),B′(-3,-),
C′(-2,-2),O′(0,-2).
15.解析 (1)C(0,2),D(4,2),
三角形AOC的面积=OA·OC=×1×2=1.
(2)当BF=CD时,三角形DFC的面积是三角形DFB面积的2倍.
∵C(0,2),D(4,2),
∴CD=4,∴BF=CD=2.
∵B(3,0),
∴F(1,0).
(3)存在,点F'的坐标为(5,0).
1
班级 姓名
第七章 平面直角坐标系
7.2 坐标方法的简单应用
7.2.2 用坐标表示平移
测试时间:20分钟
一、选择题
1.(2021湖南长沙开福青竹湖湘一外国语学校期末)点P(-1,-3)向右平移3个单位,再向上平移5个单位,则所得点的坐标为( )
A.(-4,-2) B.(-4,-8)
C.(2,2) D.(2,-8)
2.将线段AB在坐标系中平移,已知A(-1,2),B(1,1),将线段AB平移后,其两个端点的坐标变为A'(-2,1),B'(0,0),点A的对应点为点A',则它平移的情况是( )
A.向上平移了1个单位长度,向左平移了1个单位长度
B.向下平移了1个单位长度,向左平移了1个单位长度
C.向下平移了1个单位长度,向右平移了1个单位长度
D.向上平移了1个单位长度,向右平移了1个单位长度
3.(2021宁夏银川兴庆期末)如图,A,B两点的坐标分别为(-2,0),(0,1),将线段AB平移到线段A1B1的位置.若A1(b,1),B1(-1,a),则b-a的值是( )
A.-7 B.-5 C.-3 D.-1
4.(2020北京二中通州校区期末)我们规定:在平面直角坐标系xOy中,任意不重合的两点M(x1,y1),N(x2,y2)之间的折线距离为d(M,N)=|x1-x2|+|y1-y2|,例如图①中,点M(-2,3)与点N(1,-1)之间的折线距离为d(M,N)=|-2-1|+|3-(-1)|=3+4=7.如图②,已知点P的坐标为(3,-4),若点Q的坐标为(2,t),且d(P,Q)=10,则t的值为( )
A.-7或1 B.-5或13
C.5或-13 D.-1或7
5.[2020·台州]如图 ,把△ABC先向右平移3个单位,再向上平移2个单位得到△DEF,则顶点C(0,-1)的对应点的坐标为( )
A.(0,0)
B.(1,2)
C.(1,3)
D.(3,1)
6. 如图 ,在平面直角坐标系xOy中,将四边形ABCD先向下平移,再向右平移得到四边形A1B1C1D1,已知A(-3,5),B(-4,3),A1(3,3),则点B1的坐标为( )
A.(1,2)
B.(2,1)
C.(1,4)
D.(4,1)
二、填空题
7.(2021河北唐山滦州期末)把点A(3,1)向左平移2个单位,再向下平移3个单位后与点B重合,则点B的坐标是 .
8.(2021湖北武汉黄陂期末)在平面直角坐标系中,线段AB经过平移后得到线段CD,已知点A(-3,2)的对应点为C(1,-2).若点B的对应点为D(0,1),则点B的坐标为 .
9.如图,点A、B的坐标分别为(1,2)、(4,0),将△AOB沿x轴向右平移,得到△CDE,已知DB=1,则点C的坐标为 .
10.(2020广西百色二模)三角形ABC中任意一点P(x0,y0)经平移后的对应点为P1(x0+5,y0+3),将三角形ABC作同样的平移得到三角形A1B1C1,若A(-2,3),则点A的对应点A1的坐标为 .
11. 已知△A′B′C′是△ABC经过平移得到的,它们各顶点在平面直角坐标系中的坐标如下表所示:
△ABC A(a,0) B(3,0) C(5,5)
△A′B′C′ A′(4,2) B′(7,b) C′(c,7)
(1)观察并写出表中各对应点坐标的变化;
(2)确定a=________,b=________,c=________,并在图7 2 19中的平面直角坐标系中画出△ABC,△A′B′C′,并求出△ABC的面积.
三、解答题
12.(2021重庆荣昌初级中学月考)如图,直角坐标系中,三角形ABC的顶点都在格点上,其中,C点坐标为(1,-2).
(1)写出点A、B的坐标:A( , )、B( , );
(2)将三角形ABC先向右平移2个单位长度,再向上平移3个单位长度,得到三角形A1B1C1,请作出平移后的三角形A1B1C1,并直接写出三角形A1B1C1的三个顶点的坐标:A1( , )、B1( , )、C1( , );
(3)求三角形ABC的面积.
13.(2021江苏盐城盐都期末)如图,在边长为1的小正方形网格中,三角形ABC的顶点都在格点上,建立适当的平面直角坐标系xOy,使得点A、B的坐标分别为(2,3)、(3,2).
(1)画出平面直角坐标系;
(2)画出将三角形ABC沿y轴翻折,再向左平移1个单位长度得到的三角形A'B'C';
(3)点P(m,n)是△ABC内部一点,写出点P经过(2)中变换后的对应点P'的坐标: .
14.如图 ,在四边形ABCO中,AB∥OC,BC∥AO,A,C两点的坐标分别为(-,),(-2,0),A,B两点间的距离等于O,C两点间的距离.
(1)点B的坐标为________;
(2)将这个四边形向下平移2个单位长度后得到四边形A′B′C′O′,请你写出平移后四边形A′B′C′O′四个顶点的坐标.
15.(2021广西钦州期末)如图,在平面直角坐标系中,点A,B的坐标分别为(-1,0),(3,0),现同时将点A,B先向上平移2个单位长度,再向右平移1个单位长度,得到A,B的对应点C,D,连接AC,BD,CD,得到四边形ABDC.
(1)写出点C,D的坐标,并求出三角形AOC的面积;
(2)点B左侧的x轴上有一点F,使得三角形DFC的面积是三角形DFB面积的2倍,请求出点F的坐标;
(3)点B右侧的x轴上是否也存在点F',使得三角形DF'C的面积是三角形DF'B面积的2倍 若存在,请直接写出点F'的坐标;若不存在,请说明理由.
一、选择题
1.答案 C 点P(-1,-3)向右平移3个单位,再向上平移5个单位,所得到的点的坐标为(-1+3,-3+5),即(2,2),故选C.
2.答案 B 由点A,B的坐标变化可知线段AB向下平移了1个单位长度,向左平移了1个单位长度.
故选B.
3.答案 B ∵A(-2,0)平移后对应点A1的坐标为(b,1),∴线段AB向上平移了1个单位,
∵B(0,1)平移后对应点B1的坐标为(-1,a),∴线段AB向左平移了1个单位,
∴a=2,b=-3,∴b-a=-5.故选B.
4.答案 C 根据题意,得|3-2|+|-4-t|=10,
解得t=5或t=-13.
故选C.
5. 答案 D
6. 答案 B
二、填空题
7.答案 (1,-2)
解析 因为把点A(3,1)向左平移2个单位,再向下平移3个单位后与点B重合,所以点B的坐标是(3-2,1-3),
即B(1,-2),故答案为(1,-2).
8.答案 (-4,5)
解析 由点A(-3,2)的对应点为C(1,-2)可知,平移后各对应点之间的关系是横坐标加4,纵坐标减4,故点B的横坐标为-4,纵坐标为5,
即点B的坐标为(-4,5),故答案为(-4,5).
9.答案 (4,2)
解析 由已知得OD=3,
∴△AOB沿x轴向右平移了3个单位长度,
∵点A的坐标为(1,2),∴点C的坐标为(4,2).
10.答案 (3,6)
解析 ∵三角形ABC中任意一点P(x0,y0)经平移后的对应点为P1(x0+5,y0+3),
∴坐标平移规律是横坐标加5,纵坐标加3,
∵将三角形ABC作同样的平移得到三角形A1B1C1,A(-2,3),
∴A1的坐标为(-2+5,3+3),即(3,6).
11. (1)由观察,得点A,B,C分别向右平移了4个单位长度,然后向上平移了2个单位长度后分别得到了点A′,B′,C′.
(2)
S△ABC=.
三、解答题
12.解析 (1)A(-1,1),B(-3,-3).
(2)如图,三角形A1B1C1即为所求作.A1(1,4),B1(-1,0),C1(3,1).
(3)三角形ABC的面积=4×4-×2×4-×2×3-×4×1=7.
13.解析 (1)平面直角坐标系如图所示.
(2)如图,三角形A'B'C'即为所求作.
(3)P(m,n)沿y轴翻折,得到点(-m,n),再向左平移1个单位长度得到P'(-m-1,n).
14. (1)(-3,)
(2)A′(-,-),B′(-3,-),
C′(-2,-2),O′(0,-2).
15.解析 (1)C(0,2),D(4,2),
三角形AOC的面积=OA·OC=×1×2=1.
(2)当BF=CD时,三角形DFC的面积是三角形DFB面积的2倍.
∵C(0,2),D(4,2),
∴CD=4,∴BF=CD=2.
∵B(3,0),
∴F(1,0).
(3)存在,点F'的坐标为(5,0).
1
