2021-2022学年人教版九年级数学下册第27章相似 期末综合复习训练2(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学下册第27章相似 期末综合复习训练2(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 397.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-30 22:49:39 | ||
图片预览


文档简介
2021-2022学年人教版九年级数学下册《第27章相似》期末综合复习训练2(附答案)
1.若x===,则x等于( )
A.﹣1或 B.﹣1 C. D.不能确定
2.已知===,则=( )
A. B. C. D.
3.线段AB=8,P是AB的黄金分割点,且AP<BP,则BP的长度为( )
A.4﹣4 B.8+8 C.8﹣8 D.4+4
4.一个五边形ABCDE各边的边长为2,3,4,5,6,另一个和它相似的五边形A1B1C1D1E1最长边为12,则A1B1C1D1E1的最短边长为( )
A.8 B.6 C.4 D.2
5.如图,在正方形ABCD中,E,F分别是BC、AB上一点,且AF=BE,AE与DF交于点G,连接CG.若CG=BC,则AF:FB的比为( )
A.1:1 B.1:2 C.1:3 D.1:4
6.如图,AB与CD相交于点E,点F在线段BC上,且AC∥EF∥DB.若BE=5,BF=3,AE=BC,则的值为( )
A. B. C. D.
7.如图,在△ABC中,D、E为边AB的三等分点,EF∥DG∥AC,点H为AF与DG的交点.若AC=9,则DH为( )
A.1 B.2 C. D.3
8.有一个三角形木架三边长分别是15cm,20cm,24cm,现要再做一个与其相似的三角形木架,而只有长为12cm和24cm的两根木条.要求以其中一根为一边,从另一根截下两段作为另两边(允许有余料),则不同的截法有( )
A.一种 B.两种 C.三种 D.四种
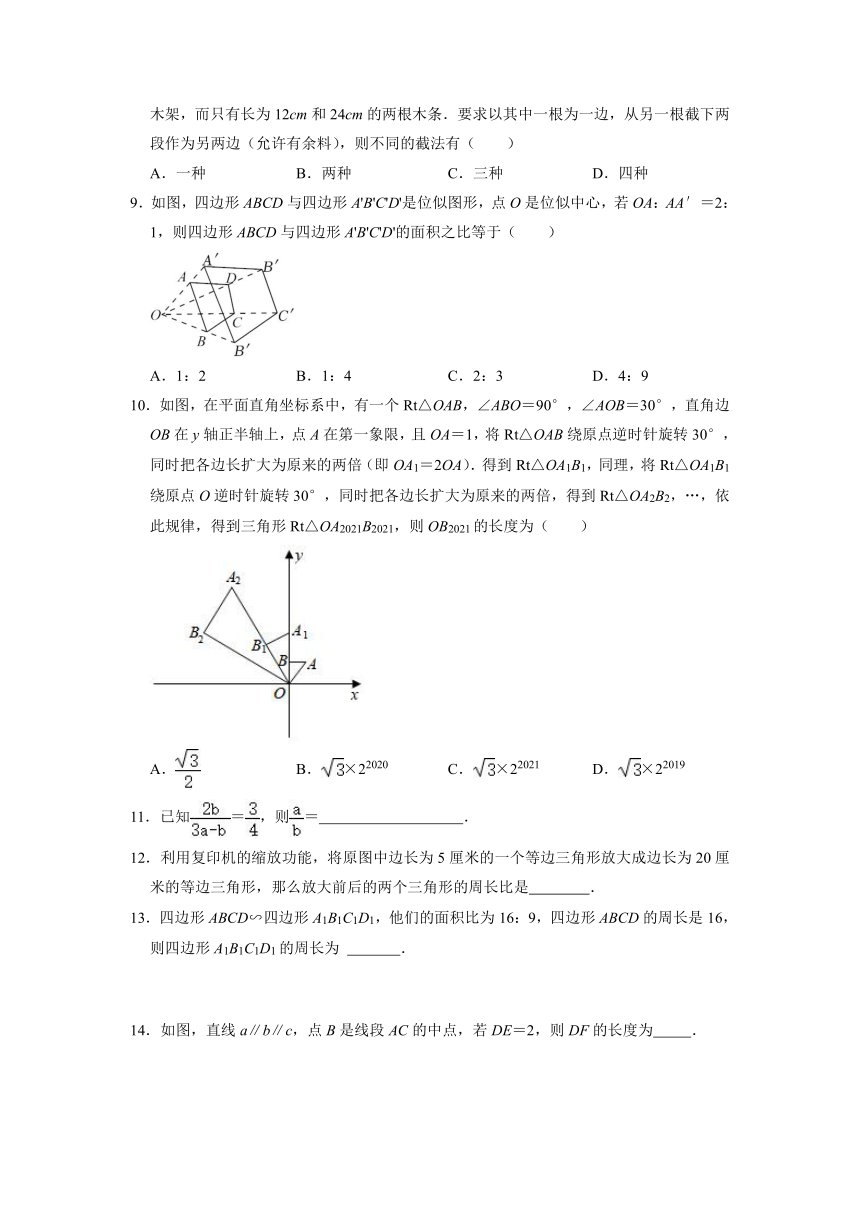
9.如图,四边形ABCD与四边形A'B'C'D'是位似图形,点O是位似中心,若OA:AA′=2:1,则四边形ABCD与四边形A'B'C'D'的面积之比等于( )
A.1:2 B.1:4 C.2:3 D.4:9
10.如图,在平面直角坐标系中,有一个Rt△OAB,∠ABO=90°,∠AOB=30°,直角边OB在y轴正半轴上,点A在第一象限,且OA=1,将Rt△OAB绕原点逆时针旋转30°,同时把各边长扩大为原来的两倍(即OA1=2OA).得到Rt△OA1B1,同理,将Rt△OA1B1绕原点O逆时针旋转30°,同时把各边长扩大为原来的两倍,得到Rt△OA2B2,…,依此规律,得到三角形Rt△OA2021B2021,则OB2021的长度为( )
A. B.×22020 C.×22021 D.×22019
11.已知=,则= .
12.利用复印机的缩放功能,将原图中边长为5厘米的一个等边三角形放大成边长为20厘米的等边三角形,那么放大前后的两个三角形的周长比是 .
13.四边形ABCD∽四边形A1B1C1D1,他们的面积比为16:9,四边形ABCD的周长是16,则四边形A1B1C1D1的周长为 .
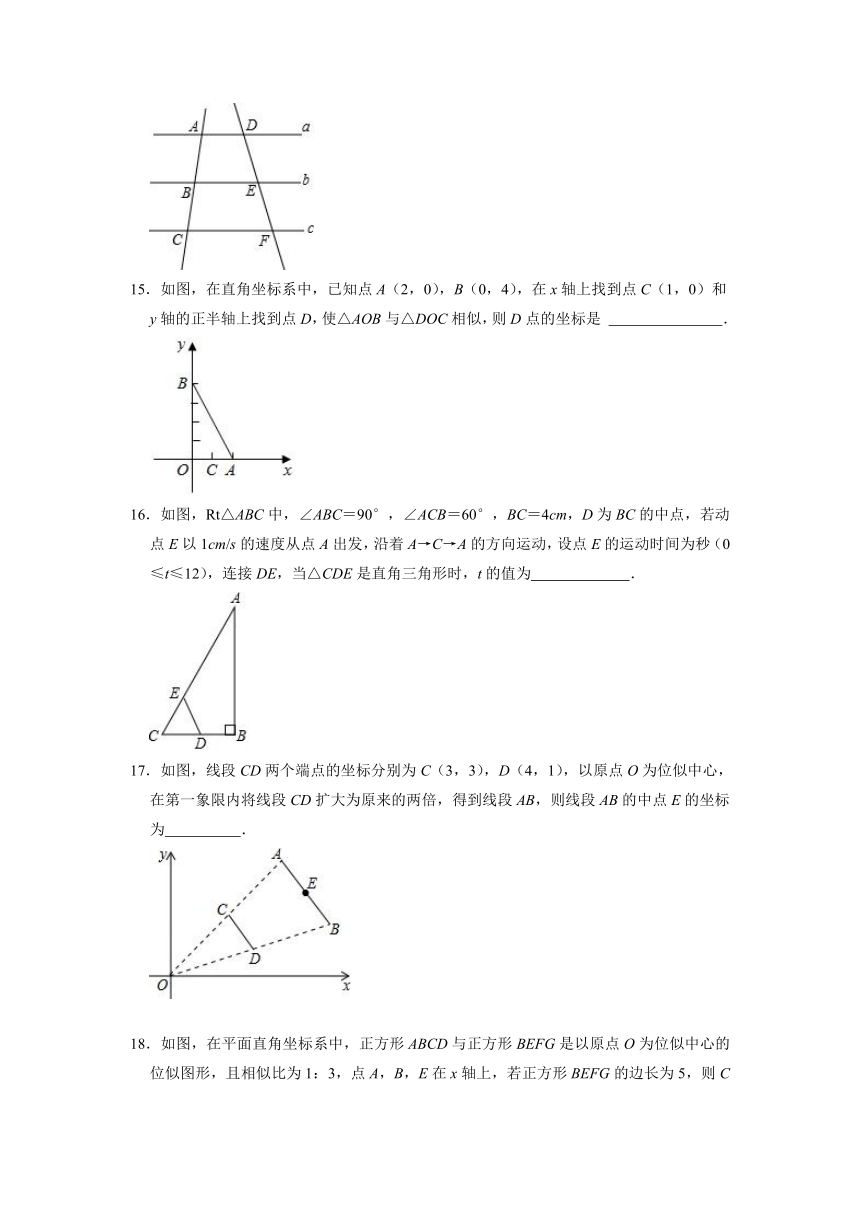
14.如图,直线a∥b∥c,点B是线段AC的中点,若DE=2,则DF的长度为 .
15.如图,在直角坐标系中,已知点A(2,0),B(0,4),在x轴上找到点C(1,0)和y轴的正半轴上找到点D,使△AOB与△DOC相似,则D点的坐标是 .
16.如图,Rt△ABC中,∠ABC=90°,∠ACB=60°,BC=4cm,D为BC的中点,若动点E以1cm/s的速度从点A出发,沿着A→C→A的方向运动,设点E的运动时间为秒(0≤t≤12),连接DE,当△CDE是直角三角形时,t的值为 .
17.如图,线段CD两个端点的坐标分别为C(3,3),D(4,1),以原点O为位似中心,在第一象限内将线段CD扩大为原来的两倍,得到线段AB,则线段AB的中点E的坐标为 .
18.如图,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为1:3,点A,B,E在x轴上,若正方形BEFG的边长为5,则C点坐标为 .
19.阅读理解:
已知:a,b,c,d都是不为0的数,且=,求证:=.
证明:∵=,∴+1=+1.∴=.
根据以上方法,解答下列问题:
(1)若=,求的值;
(2)若=,且a≠b,c≠d,证明=.
20.某校九年级数学兴趣小组在探究相似多边形问题时,他们提出了下面两个观点:
观点一:将外面大三角形按图1的方式向内缩小,得到新三角形,它们对应的边间距都为1,则新三角形与原三角形相似.
观点二:将邻边为6和10的矩形按图2的方式向内缩小,得到新的矩形,它们对应的边间距都为1,则新矩形与原矩形相似.
请回答下列问题:
(1)你认为上述两个观点是否正确?请说明理由.
(2)如图3,已知△ABC,AC=6,BC=8,AB=10,将△ABC按图3的方式向外扩张,得到△DEF,它们对应的边间距都为1,DE=15,求△DEF的面积.
21.阅读与计算,请阅读以下材料,并完成相应的问题.
角平分线分线段成比例定理,如图1,在△ABC中,AD平分∠BAC,则=.下面是这个定理的部分证明过程.
证明:如图2,过C作CE∥DA.交BA的延长线于E.…
任务:
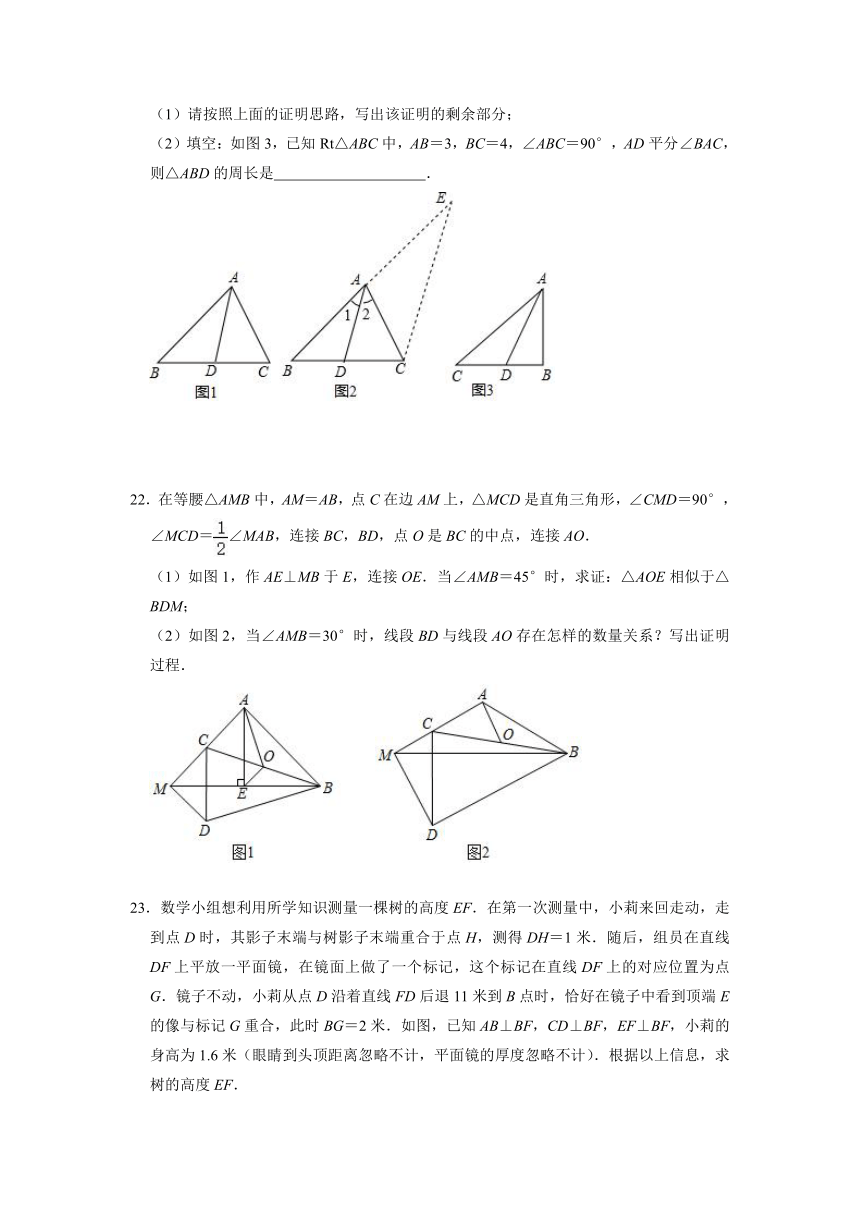
(1)请按照上面的证明思路,写出该证明的剩余部分;
(2)填空:如图3,已知Rt△ABC中,AB=3,BC=4,∠ABC=90°,AD平分∠BAC,则△ABD的周长是 .
22.在等腰△AMB中,AM=AB,点C在边AM上,△MCD是直角三角形,∠CMD=90°,∠MCD=∠MAB,连接BC,BD,点O是BC的中点,连接AO.
(1)如图1,作AE⊥MB于E,连接OE.当∠AMB=45°时,求证:△AOE相似于△BDM;
(2)如图2,当∠AMB=30°时,线段BD与线段AO存在怎样的数量关系?写出证明过程.
23.数学小组想利用所学知识测量一棵树的高度EF.在第一次测量中,小莉来回走动,走到点D时,其影子末端与树影子末端重合于点H,测得DH=1米.随后,组员在直线DF上平放一平面镜,在镜面上做了一个标记,这个标记在直线DF上的对应位置为点G.镜子不动,小莉从点D沿着直线FD后退11米到B点时,恰好在镜子中看到顶端E的像与标记G重合,此时BG=2米.如图,已知AB⊥BF,CD⊥BF,EF⊥BF,小莉的身高为1.6米(眼睛到头顶距离忽略不计,平面镜的厚度忽略不计).根据以上信息,求树的高度EF.
24.如图,点D在△ABC的边BC上,DC=AC=BD,∠ACB的平分线CF交AD于F,点E是AB的中点,连接EF.
(1)求证:△AEF∽△ABD.
(2)若△AEF的面积为1,求△ABC的面积.
参考答案
1.解:∵x===,
∴当a+b+c≠0时,x==;
当a+b+c=0时,x===﹣1,
故选:A.
2.解:∵===,
∴b=2a,d=2c,f=2e,
把b=2a,d=2c,f=2e代入===,
故选:C.
3.解:∵线段AB=8,P是AB的黄金分割点,且AP<BP,
∴BP=AB=×8=4﹣4.
故选:A.
4.解:设五边形A1B1C1D1E1的最短边长为m.
由相似多边形的性质可知:=,
∴m=4,
故选:C.
5.解:作CH⊥DF于点H,如图所示.
在△ADF和△BAE中,
,
∴△ADF≌△BAE(SAS).
∴∠ADF=∠BAE,
又∠BAE+∠GAD=90°,
∴∠ADF+∠GAD=90°,
即∠AGD=90°.
由题意可得∠ADG+∠CDG=90°,∠HDC+∠CDG=90°,.
∴∠ADG=∠HDC.
在△AGD和△DHC中,
,
∴△AGD≌△DHC(AAS).
∴DH=AG.
又CG=BC,BC=DC,
∴CG=DC.
由等腰三角形三线合一的性质可得GH=DH,
∴AG=DH=GH.
∴tan∠ADG=.
又tan∠ADF==,
∴AF=AB.
即F为AB中点,
∴AF:FB=1:1.
故选:A.
6.解:设CF=x,
∵EF∥AC,
∴=,
∴=,
解得x=,
∴CF=,
∵EF∥DB,
∴===.
故选:A.
7.解:∵D、E为边AB的三等分点,EF∥DG∥AC,
∴BE=DE=AD,BF=GF=CG,AH=HF,
∴AB=3BE,DH是△AEF的中位线,
∴DH=EF,
∵EF∥AC,
∴△BEF∽△BAC,
∴=,即 =,
解得:EF=3,
∴DH=EF=×3=,
故选:C.
8.解:长24cm的木条与三角形木架的最长边相等,要满足两边之和大于第三边,则长24cm的木条不能作为一边,
设从24cm的木条上截下两段长分别为xcm,ycm(x+y≤24),
由于长12cm的木条不能与15cm的一边对应,否则x+y>24cm,
当长12cm的木条与20cm的一边对应,则==,
解得:x=9,y=14.4;
当长12cm的木条与24cm的一边对应,则==,
解得:x=7.5,y=10.
∴有两种不同的截法:把24cm的木条截成9cm、14.4cm两段或把24cm的木条截成7.5cm、10cm两段.
故选:B.
9.解:∵OA:AA′=2:1,
∴OA:OA′=2:3.
∵四边形ABCD与四边形A′B′C′D′位似,
∴AB∥A′B′,四边形ABCD∽四边形A′B′C′D′,
∴△OAB∽△OA′B′,
∴==,
∴四边形ABCD与四边形A′B′C′D′的面积比=()2=,
故选:D.
10.解:在Rt△AOB中,∠AOB=30°,OA=1,
∴OB=OA cos∠AOB=,
由题意得,OB1=2OB=×2,
OB2=2OB1=×22,
……
OBn=2OB1=×2n=×2n﹣1,
∴OB2021=×22020.
故选:B.
11.解:∵=,
∴=,
∴﹣=,
∴=.
故答案为:.
12.解:因为原图中边长为5cm的一个等边三角形放大成边长为20cm的等边三角形,
所以放大前后的两个三角形的周长比为5:20=1:4,故答案为:1:4.
13.解:∵四边形ABCD∽四边形A1B1C1D1,他们的面积比为16:9,
∴相似比为4:3,
∴周长比等于4:3,
∴四边形A1B1C1D1的周长=×16=12,
故答案为:12.
14.解:∵点B是线段AC的中点,
∴AB=BC,
∴=1,
∵直线a∥b∥c,
∴==1,
∵DE=2,
∴EF=2,
∴DF=DE+EF=2+2=4,
故答案为:4.
15.解:若△AOB∽△DOC,点D在x轴上方:∠B=∠OCD,
∴=,即=.
∴OD=.
∴D(0,),
若△AOB∽△COD,点D在x轴上方:可得D(0,2).
综上所述,D点的坐标是(0,)或(0,2).
故答案是:(0,)或(0,2).
16.解:
在Rt△ABC中,∠ABC=90°,∠ACB=60°,BC=4cm,
∴AC=2BC=8cm,
∵D为BC中点,
∴CD=2cm,
∵0≤t≤12,
∴E点的运动路线为从A到C,再从C到AC的中点,
按运动时间分为0≤t≤8和8<t≤12两种情况,
①当0≤t≤8时,AE=tcm,CE=BC﹣AE=(8﹣t)cm,
当∠EDC=90°时,则有AB∥ED,
∵D为BC中点,
∴E为AC中点,
此时AE=4cm,可得t=4;
当∠DEC=90°时,
∵∠DEC=∠B,∠C=∠C,
∴△CED∽△BCA,
∴,即,解得t=7;
②当8<t≤12时,则此时E点又经过t=7秒时的位置,此时t=8+1=9;
当t=12时,此时E点在AC的中点,DE∥AB,此时△CDE是直角三角形.
综上可知t的值为4或7或9或12,
故答案为:4或7或9或12
17.解:∵C(3,3),D(4,1),以原点O为位似中心,在第一象限内将线段CD扩大为原来的两倍,
∴A(6,6),B(8,2),
∵E是AB中点,
∴E(7,4),
故答案为:(7,4).
18.解:∵正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为1:3,
∴=,
∵BG=5,
∴AD=BC=,
∵AD∥BG,
∴△OAD∽△OBG,
∴=,
∴=,
解得:OA=,
∴OB=+=,
∴C点坐标为:(,),
故答案为:(,).
19.解:(1)∵=,
∴=+1=+1=.
(2)∵=,
∴﹣1=﹣1,
∴=,
∵=,
∴÷=÷,
∴=.
20.解:(1)观点一正确;观点二不正确.
理由:①如图(1)连接并延长DA,交FC的延长线于点O,
∵△ABC和△DEF对应的边的距离都为1,
∴AB∥DE,AC∥DF,
∴∠FDO=∠CAO,∠ODE=∠OAB,
∴∠FDO+∠ODE=∠CAO+∠OAB,
即∠FDE=∠CAB,同理∠DEF=∠ABC,
∴△ABC∽△DEF,
∴观点一正确;
②如图(2)由题意可知,原矩形的邻边为6和10,
则新矩形邻边为4和8,
∵=,=,
∴,
∴新矩形于原矩形不相似,
∴观点二不正确;
(2)如图(3),延长DA、EB交于点O,
∵A到DE、DF的距离都为1,
∴DA是∠FDE的角平分线,
同理,EB是∠DEF的角平分线,
∴点O是△ABC的内心,
∵AC=6,BC=8,AB=10,
∴△ABC是直角三角形,
设△ABC的内切圆的半径为r,
则6﹣r+8﹣r=10,
解得r=2,
过点O作OH⊥DE于点H,交AB于G,
∵AB∥DE,
∴OG⊥AB,
∴OG=r=2,
∴==,
同理===,
∴DF=9,EF=12,
∴△DEF的面积为:×9×12=54.
21.(1)证明:如图2,过C作CE∥DA.交BA的延长线于E,
∵CE∥AD,
∴=,∠2=∠ACE,∠1=∠E,
∵∠1=∠2,
∴∠ACE=∠E,
∴AE=AC,
∴=;
(2)解:如图3,∵AB=3,BC=4,∠ABC=90°,
∴AC=5,
∵AD平分∠BAC,
∴=,即=,
∴BD=BC=,
∴AD===,
∴△ABD的周长=+3+=.
故答案为.
22.解:(1)证明:∵AM=AB,AE⊥MB,
∴E为MB的中点,
∵∠AMB=45°,
∴∠MAB=180°﹣2×45°=90°,
∴AE=MB,
∵点O是BC的中点,
∴OE∥MC且OE=MC,
∴∠OEB=∠CMB=45°,
∴∠AEO=45°,
∵∠CMD=90°,
∴∠BMD=45°,
∴∠BMD=∠AEO,
∴△BMD∽△AEO;
(2)BD=2AO;
证明:如图,作AF⊥MB于F,连接OF,
∵AM=AB,AF⊥MB,
∴F为MB的中点,
∵∠AMB=30°,
∴∠MAB=180°﹣2×30°=120°,
∴∠MCD=∠MAB=60°,
∵∠CMD=90°,
∴∠CDM=30°,
∴tanAMB=tan∠CDM=tan30°==,
∴MB=2AF,
∵点O是BC的中点,
∴OF∥MC且OF=MC,
∴∠OFB=∠CMB=30°,MD=2OF,
∴∠AFO=60°,
∴∠BMD=∠AFO,
∴△BMD∽△AFO,
∴BD=2AO.
23.解:设广告牌的高度EF为xm,
依题意知:DB=11m,BG=2m,DH=1m,AB=CD=1.6m.
∴GD=DB﹣BG=9m,
∵CD⊥BF,EF⊥BF,
∴CD∥EF.
∴△EFH∽△CDH.
∴=,即=.
∴=.
∴DF=x﹣1.
由平面镜反射规律可得:∠EGF=∠AGB.
∵AB⊥BF,
∴∠ABG=90°=∠EFG.
∴△EFG∽△ABG.
∴=,即=.
∴=.
∴x=12.8.
故树的高度EF为12.8m.
24.(1)证明:∵DC=AC,CF是∠ACB的平分线,
∴AF=DF,
∵点E是AB的中点,
即AE=BE,
∴EF是△ABD的中位线,
∴EF∥BD,
∴△AEF∽△ABD;
(2)∵△AEF∽△ABD,
∴,
∵AE=AB,S△AEF=1,
∴S△ABD=4,
∵BD=CD,
∴S△ABC=2S△ABD=8.
1.若x===,则x等于( )
A.﹣1或 B.﹣1 C. D.不能确定
2.已知===,则=( )
A. B. C. D.
3.线段AB=8,P是AB的黄金分割点,且AP<BP,则BP的长度为( )
A.4﹣4 B.8+8 C.8﹣8 D.4+4
4.一个五边形ABCDE各边的边长为2,3,4,5,6,另一个和它相似的五边形A1B1C1D1E1最长边为12,则A1B1C1D1E1的最短边长为( )
A.8 B.6 C.4 D.2
5.如图,在正方形ABCD中,E,F分别是BC、AB上一点,且AF=BE,AE与DF交于点G,连接CG.若CG=BC,则AF:FB的比为( )
A.1:1 B.1:2 C.1:3 D.1:4
6.如图,AB与CD相交于点E,点F在线段BC上,且AC∥EF∥DB.若BE=5,BF=3,AE=BC,则的值为( )
A. B. C. D.
7.如图,在△ABC中,D、E为边AB的三等分点,EF∥DG∥AC,点H为AF与DG的交点.若AC=9,则DH为( )
A.1 B.2 C. D.3
8.有一个三角形木架三边长分别是15cm,20cm,24cm,现要再做一个与其相似的三角形木架,而只有长为12cm和24cm的两根木条.要求以其中一根为一边,从另一根截下两段作为另两边(允许有余料),则不同的截法有( )
A.一种 B.两种 C.三种 D.四种
9.如图,四边形ABCD与四边形A'B'C'D'是位似图形,点O是位似中心,若OA:AA′=2:1,则四边形ABCD与四边形A'B'C'D'的面积之比等于( )
A.1:2 B.1:4 C.2:3 D.4:9
10.如图,在平面直角坐标系中,有一个Rt△OAB,∠ABO=90°,∠AOB=30°,直角边OB在y轴正半轴上,点A在第一象限,且OA=1,将Rt△OAB绕原点逆时针旋转30°,同时把各边长扩大为原来的两倍(即OA1=2OA).得到Rt△OA1B1,同理,将Rt△OA1B1绕原点O逆时针旋转30°,同时把各边长扩大为原来的两倍,得到Rt△OA2B2,…,依此规律,得到三角形Rt△OA2021B2021,则OB2021的长度为( )
A. B.×22020 C.×22021 D.×22019
11.已知=,则= .
12.利用复印机的缩放功能,将原图中边长为5厘米的一个等边三角形放大成边长为20厘米的等边三角形,那么放大前后的两个三角形的周长比是 .
13.四边形ABCD∽四边形A1B1C1D1,他们的面积比为16:9,四边形ABCD的周长是16,则四边形A1B1C1D1的周长为 .
14.如图,直线a∥b∥c,点B是线段AC的中点,若DE=2,则DF的长度为 .
15.如图,在直角坐标系中,已知点A(2,0),B(0,4),在x轴上找到点C(1,0)和y轴的正半轴上找到点D,使△AOB与△DOC相似,则D点的坐标是 .
16.如图,Rt△ABC中,∠ABC=90°,∠ACB=60°,BC=4cm,D为BC的中点,若动点E以1cm/s的速度从点A出发,沿着A→C→A的方向运动,设点E的运动时间为秒(0≤t≤12),连接DE,当△CDE是直角三角形时,t的值为 .
17.如图,线段CD两个端点的坐标分别为C(3,3),D(4,1),以原点O为位似中心,在第一象限内将线段CD扩大为原来的两倍,得到线段AB,则线段AB的中点E的坐标为 .
18.如图,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为1:3,点A,B,E在x轴上,若正方形BEFG的边长为5,则C点坐标为 .
19.阅读理解:
已知:a,b,c,d都是不为0的数,且=,求证:=.
证明:∵=,∴+1=+1.∴=.
根据以上方法,解答下列问题:
(1)若=,求的值;
(2)若=,且a≠b,c≠d,证明=.
20.某校九年级数学兴趣小组在探究相似多边形问题时,他们提出了下面两个观点:
观点一:将外面大三角形按图1的方式向内缩小,得到新三角形,它们对应的边间距都为1,则新三角形与原三角形相似.
观点二:将邻边为6和10的矩形按图2的方式向内缩小,得到新的矩形,它们对应的边间距都为1,则新矩形与原矩形相似.
请回答下列问题:
(1)你认为上述两个观点是否正确?请说明理由.
(2)如图3,已知△ABC,AC=6,BC=8,AB=10,将△ABC按图3的方式向外扩张,得到△DEF,它们对应的边间距都为1,DE=15,求△DEF的面积.
21.阅读与计算,请阅读以下材料,并完成相应的问题.
角平分线分线段成比例定理,如图1,在△ABC中,AD平分∠BAC,则=.下面是这个定理的部分证明过程.
证明:如图2,过C作CE∥DA.交BA的延长线于E.…
任务:
(1)请按照上面的证明思路,写出该证明的剩余部分;
(2)填空:如图3,已知Rt△ABC中,AB=3,BC=4,∠ABC=90°,AD平分∠BAC,则△ABD的周长是 .
22.在等腰△AMB中,AM=AB,点C在边AM上,△MCD是直角三角形,∠CMD=90°,∠MCD=∠MAB,连接BC,BD,点O是BC的中点,连接AO.
(1)如图1,作AE⊥MB于E,连接OE.当∠AMB=45°时,求证:△AOE相似于△BDM;
(2)如图2,当∠AMB=30°时,线段BD与线段AO存在怎样的数量关系?写出证明过程.
23.数学小组想利用所学知识测量一棵树的高度EF.在第一次测量中,小莉来回走动,走到点D时,其影子末端与树影子末端重合于点H,测得DH=1米.随后,组员在直线DF上平放一平面镜,在镜面上做了一个标记,这个标记在直线DF上的对应位置为点G.镜子不动,小莉从点D沿着直线FD后退11米到B点时,恰好在镜子中看到顶端E的像与标记G重合,此时BG=2米.如图,已知AB⊥BF,CD⊥BF,EF⊥BF,小莉的身高为1.6米(眼睛到头顶距离忽略不计,平面镜的厚度忽略不计).根据以上信息,求树的高度EF.
24.如图,点D在△ABC的边BC上,DC=AC=BD,∠ACB的平分线CF交AD于F,点E是AB的中点,连接EF.
(1)求证:△AEF∽△ABD.
(2)若△AEF的面积为1,求△ABC的面积.
参考答案
1.解:∵x===,
∴当a+b+c≠0时,x==;
当a+b+c=0时,x===﹣1,
故选:A.
2.解:∵===,
∴b=2a,d=2c,f=2e,
把b=2a,d=2c,f=2e代入===,
故选:C.
3.解:∵线段AB=8,P是AB的黄金分割点,且AP<BP,
∴BP=AB=×8=4﹣4.
故选:A.
4.解:设五边形A1B1C1D1E1的最短边长为m.
由相似多边形的性质可知:=,
∴m=4,
故选:C.
5.解:作CH⊥DF于点H,如图所示.
在△ADF和△BAE中,
,
∴△ADF≌△BAE(SAS).
∴∠ADF=∠BAE,
又∠BAE+∠GAD=90°,
∴∠ADF+∠GAD=90°,
即∠AGD=90°.
由题意可得∠ADG+∠CDG=90°,∠HDC+∠CDG=90°,.
∴∠ADG=∠HDC.
在△AGD和△DHC中,
,
∴△AGD≌△DHC(AAS).
∴DH=AG.
又CG=BC,BC=DC,
∴CG=DC.
由等腰三角形三线合一的性质可得GH=DH,
∴AG=DH=GH.
∴tan∠ADG=.
又tan∠ADF==,
∴AF=AB.
即F为AB中点,
∴AF:FB=1:1.
故选:A.
6.解:设CF=x,
∵EF∥AC,
∴=,
∴=,
解得x=,
∴CF=,
∵EF∥DB,
∴===.
故选:A.
7.解:∵D、E为边AB的三等分点,EF∥DG∥AC,
∴BE=DE=AD,BF=GF=CG,AH=HF,
∴AB=3BE,DH是△AEF的中位线,
∴DH=EF,
∵EF∥AC,
∴△BEF∽△BAC,
∴=,即 =,
解得:EF=3,
∴DH=EF=×3=,
故选:C.
8.解:长24cm的木条与三角形木架的最长边相等,要满足两边之和大于第三边,则长24cm的木条不能作为一边,
设从24cm的木条上截下两段长分别为xcm,ycm(x+y≤24),
由于长12cm的木条不能与15cm的一边对应,否则x+y>24cm,
当长12cm的木条与20cm的一边对应,则==,
解得:x=9,y=14.4;
当长12cm的木条与24cm的一边对应,则==,
解得:x=7.5,y=10.
∴有两种不同的截法:把24cm的木条截成9cm、14.4cm两段或把24cm的木条截成7.5cm、10cm两段.
故选:B.
9.解:∵OA:AA′=2:1,
∴OA:OA′=2:3.
∵四边形ABCD与四边形A′B′C′D′位似,
∴AB∥A′B′,四边形ABCD∽四边形A′B′C′D′,
∴△OAB∽△OA′B′,
∴==,
∴四边形ABCD与四边形A′B′C′D′的面积比=()2=,
故选:D.
10.解:在Rt△AOB中,∠AOB=30°,OA=1,
∴OB=OA cos∠AOB=,
由题意得,OB1=2OB=×2,
OB2=2OB1=×22,
……
OBn=2OB1=×2n=×2n﹣1,
∴OB2021=×22020.
故选:B.
11.解:∵=,
∴=,
∴﹣=,
∴=.
故答案为:.
12.解:因为原图中边长为5cm的一个等边三角形放大成边长为20cm的等边三角形,
所以放大前后的两个三角形的周长比为5:20=1:4,故答案为:1:4.
13.解:∵四边形ABCD∽四边形A1B1C1D1,他们的面积比为16:9,
∴相似比为4:3,
∴周长比等于4:3,
∴四边形A1B1C1D1的周长=×16=12,
故答案为:12.
14.解:∵点B是线段AC的中点,
∴AB=BC,
∴=1,
∵直线a∥b∥c,
∴==1,
∵DE=2,
∴EF=2,
∴DF=DE+EF=2+2=4,
故答案为:4.
15.解:若△AOB∽△DOC,点D在x轴上方:∠B=∠OCD,
∴=,即=.
∴OD=.
∴D(0,),
若△AOB∽△COD,点D在x轴上方:可得D(0,2).
综上所述,D点的坐标是(0,)或(0,2).
故答案是:(0,)或(0,2).
16.解:
在Rt△ABC中,∠ABC=90°,∠ACB=60°,BC=4cm,
∴AC=2BC=8cm,
∵D为BC中点,
∴CD=2cm,
∵0≤t≤12,
∴E点的运动路线为从A到C,再从C到AC的中点,
按运动时间分为0≤t≤8和8<t≤12两种情况,
①当0≤t≤8时,AE=tcm,CE=BC﹣AE=(8﹣t)cm,
当∠EDC=90°时,则有AB∥ED,
∵D为BC中点,
∴E为AC中点,
此时AE=4cm,可得t=4;
当∠DEC=90°时,
∵∠DEC=∠B,∠C=∠C,
∴△CED∽△BCA,
∴,即,解得t=7;
②当8<t≤12时,则此时E点又经过t=7秒时的位置,此时t=8+1=9;
当t=12时,此时E点在AC的中点,DE∥AB,此时△CDE是直角三角形.
综上可知t的值为4或7或9或12,
故答案为:4或7或9或12
17.解:∵C(3,3),D(4,1),以原点O为位似中心,在第一象限内将线段CD扩大为原来的两倍,
∴A(6,6),B(8,2),
∵E是AB中点,
∴E(7,4),
故答案为:(7,4).
18.解:∵正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为1:3,
∴=,
∵BG=5,
∴AD=BC=,
∵AD∥BG,
∴△OAD∽△OBG,
∴=,
∴=,
解得:OA=,
∴OB=+=,
∴C点坐标为:(,),
故答案为:(,).
19.解:(1)∵=,
∴=+1=+1=.
(2)∵=,
∴﹣1=﹣1,
∴=,
∵=,
∴÷=÷,
∴=.
20.解:(1)观点一正确;观点二不正确.
理由:①如图(1)连接并延长DA,交FC的延长线于点O,
∵△ABC和△DEF对应的边的距离都为1,
∴AB∥DE,AC∥DF,
∴∠FDO=∠CAO,∠ODE=∠OAB,
∴∠FDO+∠ODE=∠CAO+∠OAB,
即∠FDE=∠CAB,同理∠DEF=∠ABC,
∴△ABC∽△DEF,
∴观点一正确;
②如图(2)由题意可知,原矩形的邻边为6和10,
则新矩形邻边为4和8,
∵=,=,
∴,
∴新矩形于原矩形不相似,
∴观点二不正确;
(2)如图(3),延长DA、EB交于点O,
∵A到DE、DF的距离都为1,
∴DA是∠FDE的角平分线,
同理,EB是∠DEF的角平分线,
∴点O是△ABC的内心,
∵AC=6,BC=8,AB=10,
∴△ABC是直角三角形,
设△ABC的内切圆的半径为r,
则6﹣r+8﹣r=10,
解得r=2,
过点O作OH⊥DE于点H,交AB于G,
∵AB∥DE,
∴OG⊥AB,
∴OG=r=2,
∴==,
同理===,
∴DF=9,EF=12,
∴△DEF的面积为:×9×12=54.
21.(1)证明:如图2,过C作CE∥DA.交BA的延长线于E,
∵CE∥AD,
∴=,∠2=∠ACE,∠1=∠E,
∵∠1=∠2,
∴∠ACE=∠E,
∴AE=AC,
∴=;
(2)解:如图3,∵AB=3,BC=4,∠ABC=90°,
∴AC=5,
∵AD平分∠BAC,
∴=,即=,
∴BD=BC=,
∴AD===,
∴△ABD的周长=+3+=.
故答案为.
22.解:(1)证明:∵AM=AB,AE⊥MB,
∴E为MB的中点,
∵∠AMB=45°,
∴∠MAB=180°﹣2×45°=90°,
∴AE=MB,
∵点O是BC的中点,
∴OE∥MC且OE=MC,
∴∠OEB=∠CMB=45°,
∴∠AEO=45°,
∵∠CMD=90°,
∴∠BMD=45°,
∴∠BMD=∠AEO,
∴△BMD∽△AEO;
(2)BD=2AO;
证明:如图,作AF⊥MB于F,连接OF,
∵AM=AB,AF⊥MB,
∴F为MB的中点,
∵∠AMB=30°,
∴∠MAB=180°﹣2×30°=120°,
∴∠MCD=∠MAB=60°,
∵∠CMD=90°,
∴∠CDM=30°,
∴tanAMB=tan∠CDM=tan30°==,
∴MB=2AF,
∵点O是BC的中点,
∴OF∥MC且OF=MC,
∴∠OFB=∠CMB=30°,MD=2OF,
∴∠AFO=60°,
∴∠BMD=∠AFO,
∴△BMD∽△AFO,
∴BD=2AO.
23.解:设广告牌的高度EF为xm,
依题意知:DB=11m,BG=2m,DH=1m,AB=CD=1.6m.
∴GD=DB﹣BG=9m,
∵CD⊥BF,EF⊥BF,
∴CD∥EF.
∴△EFH∽△CDH.
∴=,即=.
∴=.
∴DF=x﹣1.
由平面镜反射规律可得:∠EGF=∠AGB.
∵AB⊥BF,
∴∠ABG=90°=∠EFG.
∴△EFG∽△ABG.
∴=,即=.
∴=.
∴x=12.8.
故树的高度EF为12.8m.
24.(1)证明:∵DC=AC,CF是∠ACB的平分线,
∴AF=DF,
∵点E是AB的中点,
即AE=BE,
∴EF是△ABD的中位线,
∴EF∥BD,
∴△AEF∽△ABD;
(2)∵△AEF∽△ABD,
∴,
∵AE=AB,S△AEF=1,
∴S△ABD=4,
∵BD=CD,
∴S△ABC=2S△ABD=8.
