北师大版七下数学4.3探索三角形全等的条件(第1课时)课件(25张ppt)
文档属性
| 名称 | 北师大版七下数学4.3探索三角形全等的条件(第1课时)课件(25张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 875.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-31 09:16:09 | ||
图片预览





文档简介
(共25张PPT)
第四章 三角形
3 探索三角形全等的条件(第1课时)
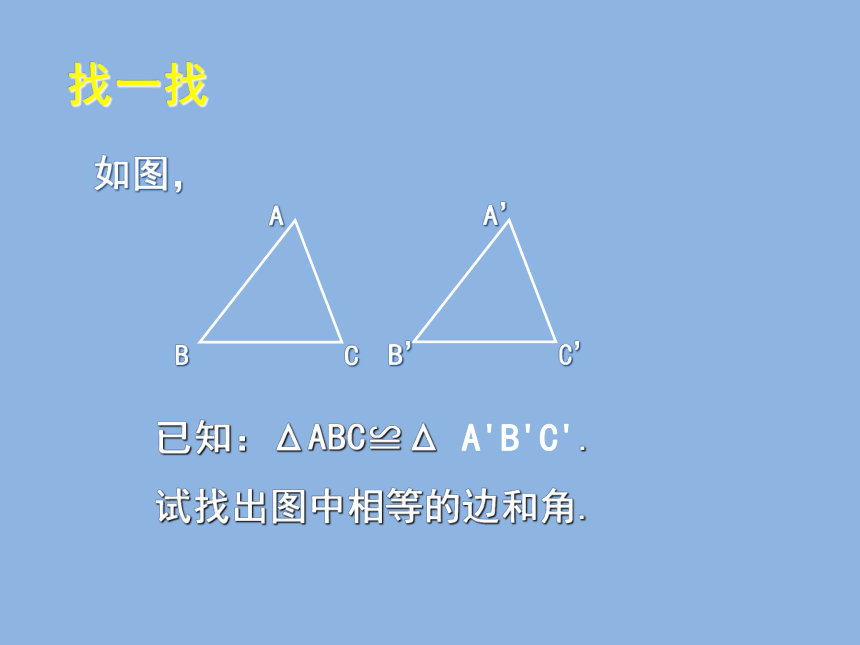
找一找
如图,
A
B
C
已知:ΔABC≌Δ A'B'C'.
试找出图中相等的边和角.
A’
B’
C’
生活中的数学
小明家衣橱上两块全等的三角形玻璃装饰物,其中一块被打碎了,妈妈让小明快速配一块回来,如果只有一把尺子,小明该怎么办?
要画一个三角形与小明画的三角形全等,需要几个与边或角的大小有关的条件呢?
想一想
做一做
1. 只给一个条件(一条边或一个角)画三角形时,大家画出的三角形一定全等吗?
请大家动手在学案上画一画,然后互相比比看。
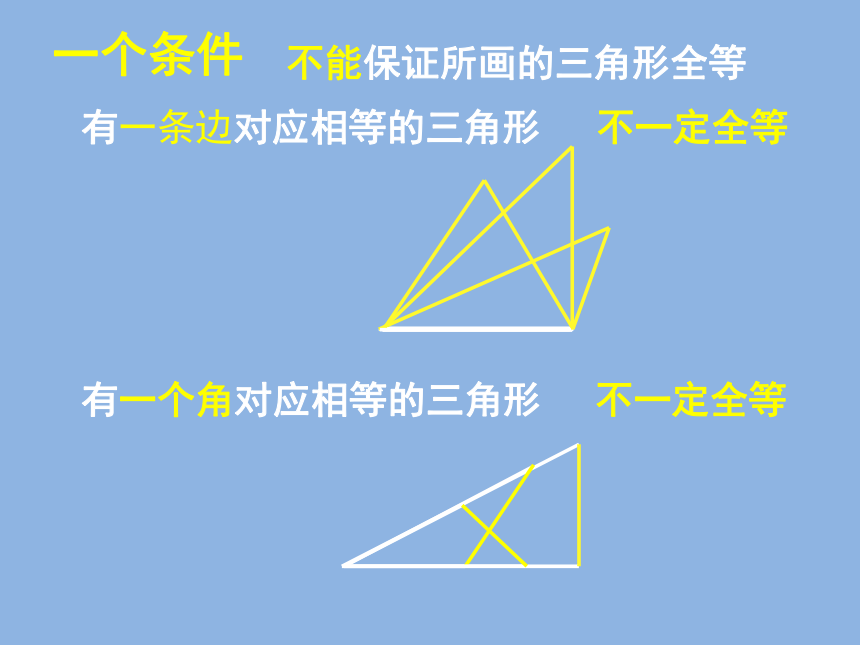
一个条件
有一条边对应相等的三角形
不一定全等
有一个角对应相等的三角形
不一定全等
不能保证所画的三角形全等
2. 给出两个条件画三角形时,有几种可能的情况?每种情况下作出的三角形一定全等吗?分别按照下面的条件做一做。
做一做
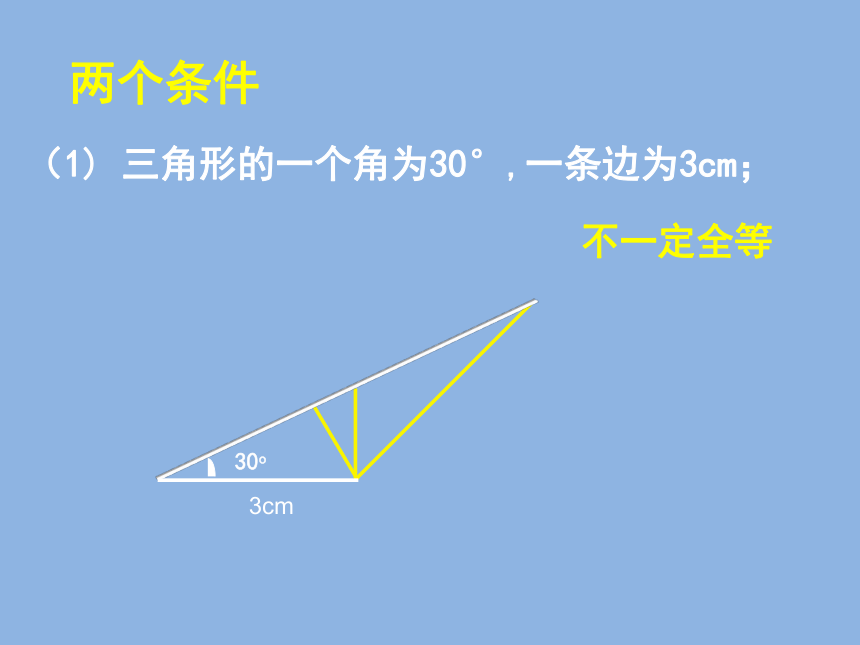
(1) 三角形的一个内角为30°,一条边为3cm;
(1) 三角形的一个角为30°,一条边为3cm;
不一定全等
两个条件
30o
3cm
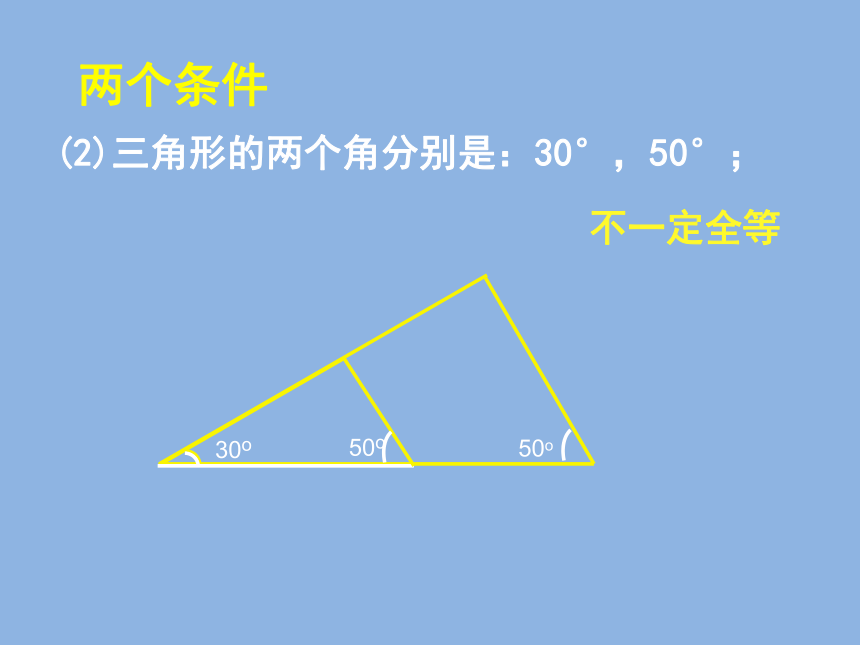
(2)三角形的两个角分别是:30°,50°;
不一定全等
50o
50o
两个条件
30o
(3)三角形的两条边分别是:4cm,6cm.
不一定全等
4cm
4cm
6cm
4cm
也不能保证三角形全等.
两个条件
2. 给出两个条件画三角形时,有几种可能的情况?每种情况下作出的三角形一定全等吗?分别按照下面的条件做一做。
结论
1. 只给一个条件(一条边或一个角)画三角形时,大家画出的三角形一定全等吗?
不一定全等
(3) 三角形的两条边分别为4cm,6cm.
(1) 三角形的一个内角为30°,一条边为3cm;
(2) 三角形的两个内角分别为30°和 50°;
不一定全等
议一议
如果给出三个条件画三角形,你能说出有哪几种可能的情况吗?
1.三个角
2.三条边
3.两边一角
4.两角一边
做一做
(1) 已知一个三角形的三个内角分别为40°,60°和80°,你能画出这个三角形吗?把你画的三角形与同伴画出的进行比较,它们一定全等吗?
三个内角对应相等的两个三角形不一定全等
做一做
(2) 已知一个三角形的三条边分别为4cm,5cm和7cm,你能画出这个三角形吗?把你画的三角形与同伴画出的进行比较,它们一定全等吗?
三边对应相等的两个三角形全等,简写为“边边边”或“SSS”。
AB=A’B’
BC=B’C’
AC=A’C’
(SSS)
A’
B’
C’
A
B
C
数学表达式:
在△ABC和△A'B'C'中
ABC ≌ A'B'C'
所以
动手做一做
准备几根硬纸条
(1)取出三根硬纸条钉成一个三角形,你能拉动其中两边,使这个三角形的形状发生变化吗?
(2)取出四根硬纸条钉成一个四边形,拉动其中两边,这个四边形的形状改变了吗?钉成 一个五边形,又会怎么样?
(3)上面的现象说明了什么?
三角形的框架,它的大小和形状是固定不变的,三角形的这个性质叫做三角形的稳定性。
你能举几个应用三角形稳定性的例子吗?
你能找到图中的三角形吗?
你能说出为什么这些地方是三角形吗
范例点击
如图,△ABC中 AB=AC, D为BC中点
试说明:①△ABD≌△ACD.
②∠BAD=∠CAD
③AD⊥BC
C
D
B
A
问题解决
用本节所学知识解决第二环节中提出的“情景问题”。
变式训练
如图,已知AC=FE、BC=DE,点A、D 、B、F在一条直线上,AD=FB.要用“边边边 ”证明△ABC≌△FDE,除了已知中的AC=FE,BC=DE以外,还应该有什么条件?怎样才能得到这个条件?
F
D
C
B
E
A
这节课你学到了什么?
1.确定三角形全等的条件至少要几个?今天我们学习了用什么方法说明三角形全等?
三边对应相等的两个三角形全等
(“边边边”或“SSS”)
3.三角形具有稳定性。
2.今天在探索三角形全等条件的过程中,我们用到了什么数学思想?运用这种数学思想我们要注意什么?
如图所示,已知:AB=DC,AC=DB,那么△ABC和△DCB全等吗?请说明理由。
分层作业B2
C
D
A
B
如图,已知AB=CD,AC=BD。∠A和∠D相等吗?试说明理由
分层作业C2
D
C
A
E
B
提示:连接BC
第四章 三角形
3 探索三角形全等的条件(第1课时)
找一找
如图,
A
B
C
已知:ΔABC≌Δ A'B'C'.
试找出图中相等的边和角.
A’
B’
C’
生活中的数学
小明家衣橱上两块全等的三角形玻璃装饰物,其中一块被打碎了,妈妈让小明快速配一块回来,如果只有一把尺子,小明该怎么办?
要画一个三角形与小明画的三角形全等,需要几个与边或角的大小有关的条件呢?
想一想
做一做
1. 只给一个条件(一条边或一个角)画三角形时,大家画出的三角形一定全等吗?
请大家动手在学案上画一画,然后互相比比看。
一个条件
有一条边对应相等的三角形
不一定全等
有一个角对应相等的三角形
不一定全等
不能保证所画的三角形全等
2. 给出两个条件画三角形时,有几种可能的情况?每种情况下作出的三角形一定全等吗?分别按照下面的条件做一做。
做一做
(1) 三角形的一个内角为30°,一条边为3cm;
(1) 三角形的一个角为30°,一条边为3cm;
不一定全等
两个条件
30o
3cm
(2)三角形的两个角分别是:30°,50°;
不一定全等
50o
50o
两个条件
30o
(3)三角形的两条边分别是:4cm,6cm.
不一定全等
4cm
4cm
6cm
4cm
也不能保证三角形全等.
两个条件
2. 给出两个条件画三角形时,有几种可能的情况?每种情况下作出的三角形一定全等吗?分别按照下面的条件做一做。
结论
1. 只给一个条件(一条边或一个角)画三角形时,大家画出的三角形一定全等吗?
不一定全等
(3) 三角形的两条边分别为4cm,6cm.
(1) 三角形的一个内角为30°,一条边为3cm;
(2) 三角形的两个内角分别为30°和 50°;
不一定全等
议一议
如果给出三个条件画三角形,你能说出有哪几种可能的情况吗?
1.三个角
2.三条边
3.两边一角
4.两角一边
做一做
(1) 已知一个三角形的三个内角分别为40°,60°和80°,你能画出这个三角形吗?把你画的三角形与同伴画出的进行比较,它们一定全等吗?
三个内角对应相等的两个三角形不一定全等
做一做
(2) 已知一个三角形的三条边分别为4cm,5cm和7cm,你能画出这个三角形吗?把你画的三角形与同伴画出的进行比较,它们一定全等吗?
三边对应相等的两个三角形全等,简写为“边边边”或“SSS”。
AB=A’B’
BC=B’C’
AC=A’C’
(SSS)
A’
B’
C’
A
B
C
数学表达式:
在△ABC和△A'B'C'中
ABC ≌ A'B'C'
所以
动手做一做
准备几根硬纸条
(1)取出三根硬纸条钉成一个三角形,你能拉动其中两边,使这个三角形的形状发生变化吗?
(2)取出四根硬纸条钉成一个四边形,拉动其中两边,这个四边形的形状改变了吗?钉成 一个五边形,又会怎么样?
(3)上面的现象说明了什么?
三角形的框架,它的大小和形状是固定不变的,三角形的这个性质叫做三角形的稳定性。
你能举几个应用三角形稳定性的例子吗?
你能找到图中的三角形吗?
你能说出为什么这些地方是三角形吗
范例点击
如图,△ABC中 AB=AC, D为BC中点
试说明:①△ABD≌△ACD.
②∠BAD=∠CAD
③AD⊥BC
C
D
B
A
问题解决
用本节所学知识解决第二环节中提出的“情景问题”。
变式训练
如图,已知AC=FE、BC=DE,点A、D 、B、F在一条直线上,AD=FB.要用“边边边 ”证明△ABC≌△FDE,除了已知中的AC=FE,BC=DE以外,还应该有什么条件?怎样才能得到这个条件?
F
D
C
B
E
A
这节课你学到了什么?
1.确定三角形全等的条件至少要几个?今天我们学习了用什么方法说明三角形全等?
三边对应相等的两个三角形全等
(“边边边”或“SSS”)
3.三角形具有稳定性。
2.今天在探索三角形全等条件的过程中,我们用到了什么数学思想?运用这种数学思想我们要注意什么?
如图所示,已知:AB=DC,AC=DB,那么△ABC和△DCB全等吗?请说明理由。
分层作业B2
C
D
A
B
如图,已知AB=CD,AC=BD。∠A和∠D相等吗?试说明理由
分层作业C2
D
C
A
E
B
提示:连接BC
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
