5.3.1函数的单调性-2021-2022学年高二上学期数学 人教A版(2019)选择性必修第二册 课件(共20张PPT)
文档属性
| 名称 | 5.3.1函数的单调性-2021-2022学年高二上学期数学 人教A版(2019)选择性必修第二册 课件(共20张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-31 08:48:19 | ||
图片预览




文档简介
(共20张PPT)
1、了解可导函数的单调性与其导数的关系;
2、掌握利用导数判断函数单调性的方法。
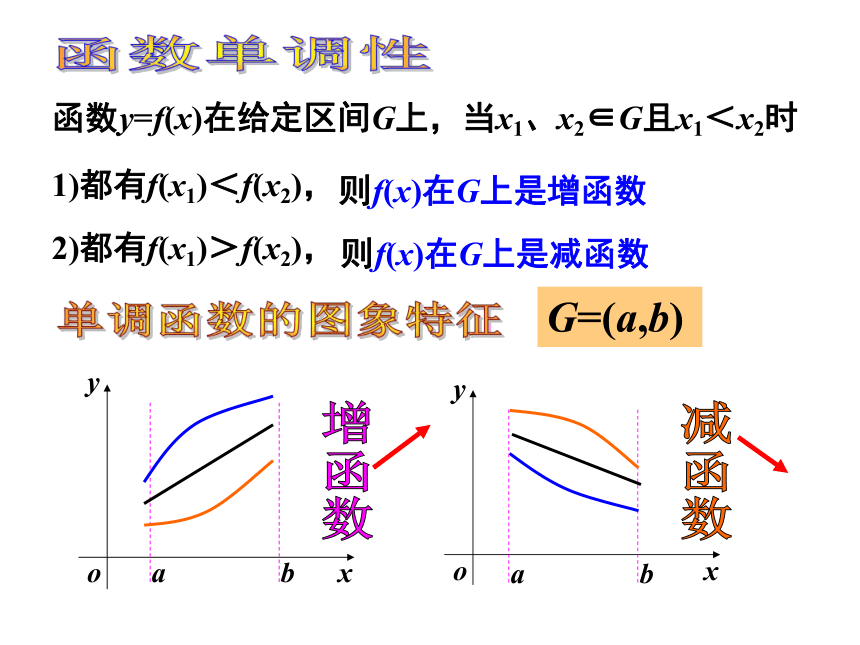
函数y=f(x)在给定区间G上,当x1、x2∈G且x1<x2时
y
x
o
a
b
y
x
o
a
b
1)都有f(x1)<f(x2),
则f(x)在G上是增函数
2)都有f(x1)>f(x2),
则f(x)在G上是减函数
G=(a,b)
判断函数单调性有哪些方法?
例如:判断函数 的单调性。
x
y
o
函数在 上为 函数,
在 上为 函数。
图象法
定义法
减
增
如图:
x
y
O
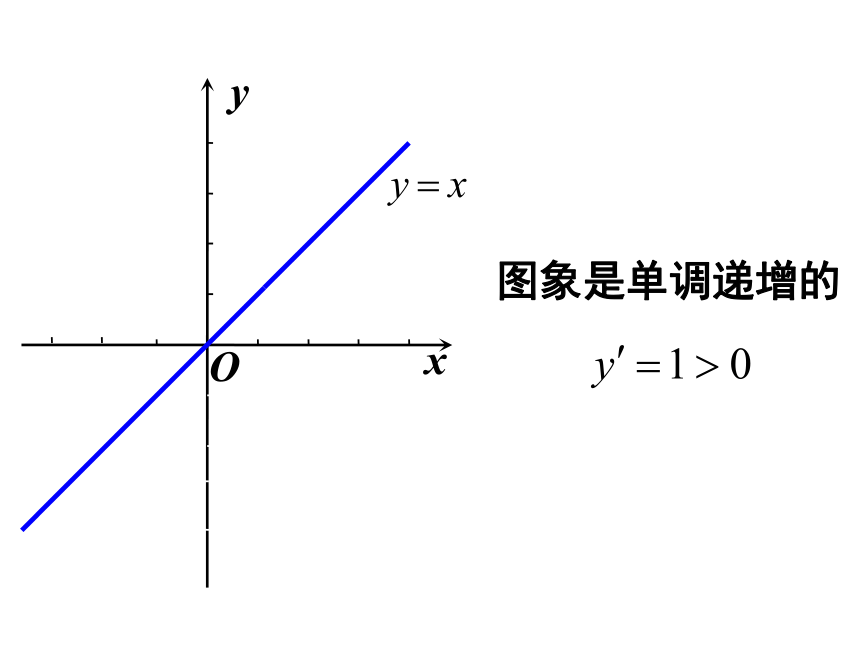
图象是单调递增的
x
y
O
图象是单调递减的
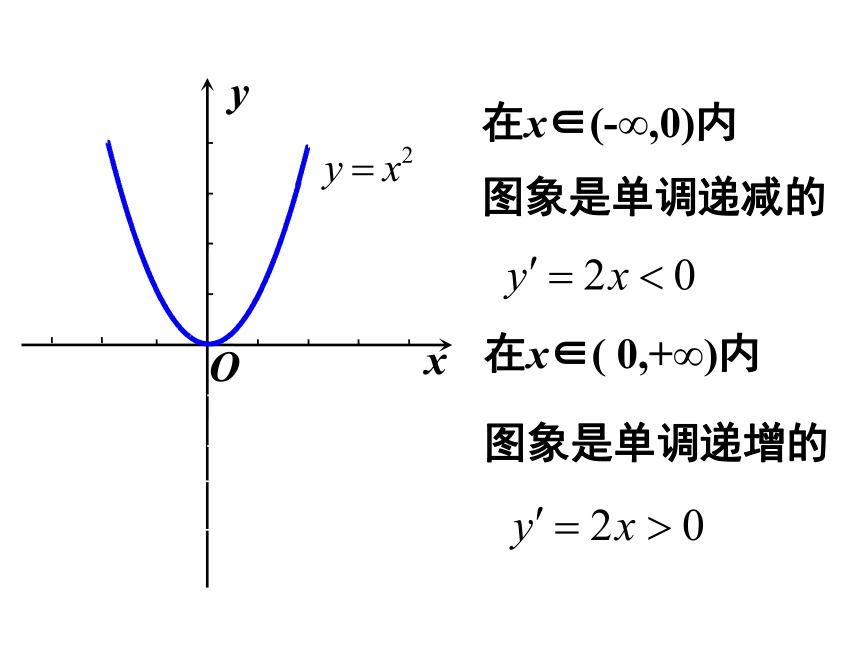
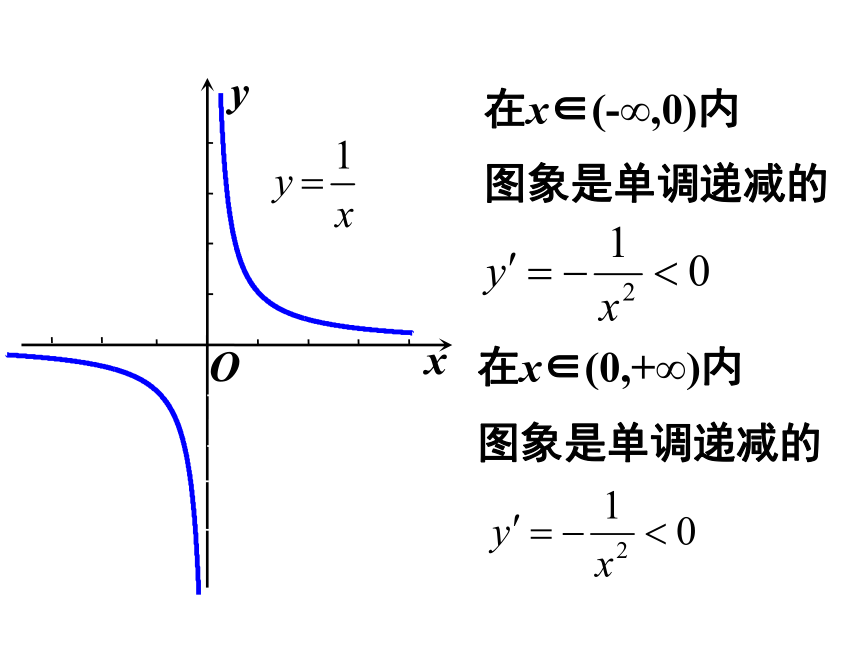
在x∈(-∞,0)内
图象是单调递增的
在x∈( 0,+∞)内
x
y
O
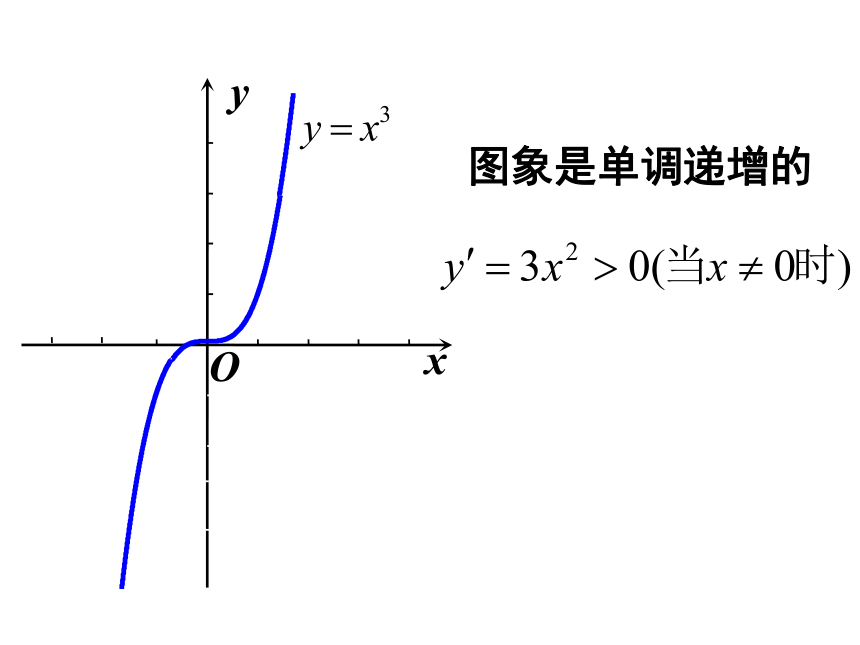
图象是单调递增的
x
y
O
图象是单调递减的
在x∈(-∞,0)内
图象是单调递减的
在x∈(0,+∞)内
当函数 y=f (x) 在区间 内可导时,
注意:
应正确理解“某个区间”的含义,它必须是定义域内的某个区间。
例1:求函数 的单调区间。
解:
单调递增区间为:
单调递减区间为:
例1:求函数 的单调区间。
解:
变式1:求函数 的单调区间。
单调递增区间为:
单调递减区间为:
例1:求函数 的单调区间。
变式1:求函数 的单调区间。
变式2:求函数 的单调区间。
解:
单调递增区间为:
单调递减区间为:
当函数 y=f (x) 在区间 内可导时,
充分不必要条件
当函数 y=f (x) 在区间 内可导时,
练习:求下列函数的单调区间。
解:
单调递增区间为:
单调递减区间为:
练习:求下列函数的单调区间。
解:
单调递减区间为:
练习:求下列函数的单调区间。
解:
单调递增区间为:
单调递减区间为:
总结: 当遇到三次或三次以上的,或图象很难
画出的函数求单调性问题时,应考虑导数法。
(1)求函数定义域
(2)求
(3)令
(4)写出单调区间
1、什么情况下,用“导数法” 求函数单调性、 单调区间较简便?
2、总结用“导数法” 求单调区间的步骤?
例2:如图,水以常速(即单位时间内注入水的
体积相同)注入下面四种底面积相同的容器中,请分别找出与各容器对应的水的高度h与
时间t的函数关系图象。
h
O
t
h
O
t
h
O
t
h
O
(A)
(B)
(C)
(D)
(1)
(2)
(3)
(4)
【总一总★成竹在胸】
当函数 y=f (x) 在区间 内可导时,
1、了解可导函数的单调性与其导数的关系;
2、掌握利用导数判断函数单调性的方法。
函数y=f(x)在给定区间G上,当x1、x2∈G且x1<x2时
y
x
o
a
b
y
x
o
a
b
1)都有f(x1)<f(x2),
则f(x)在G上是增函数
2)都有f(x1)>f(x2),
则f(x)在G上是减函数
G=(a,b)
判断函数单调性有哪些方法?
例如:判断函数 的单调性。
x
y
o
函数在 上为 函数,
在 上为 函数。
图象法
定义法
减
增
如图:
x
y
O
图象是单调递增的
x
y
O
图象是单调递减的
在x∈(-∞,0)内
图象是单调递增的
在x∈( 0,+∞)内
x
y
O
图象是单调递增的
x
y
O
图象是单调递减的
在x∈(-∞,0)内
图象是单调递减的
在x∈(0,+∞)内
当函数 y=f (x) 在区间 内可导时,
注意:
应正确理解“某个区间”的含义,它必须是定义域内的某个区间。
例1:求函数 的单调区间。
解:
单调递增区间为:
单调递减区间为:
例1:求函数 的单调区间。
解:
变式1:求函数 的单调区间。
单调递增区间为:
单调递减区间为:
例1:求函数 的单调区间。
变式1:求函数 的单调区间。
变式2:求函数 的单调区间。
解:
单调递增区间为:
单调递减区间为:
当函数 y=f (x) 在区间 内可导时,
充分不必要条件
当函数 y=f (x) 在区间 内可导时,
练习:求下列函数的单调区间。
解:
单调递增区间为:
单调递减区间为:
练习:求下列函数的单调区间。
解:
单调递减区间为:
练习:求下列函数的单调区间。
解:
单调递增区间为:
单调递减区间为:
总结: 当遇到三次或三次以上的,或图象很难
画出的函数求单调性问题时,应考虑导数法。
(1)求函数定义域
(2)求
(3)令
(4)写出单调区间
1、什么情况下,用“导数法” 求函数单调性、 单调区间较简便?
2、总结用“导数法” 求单调区间的步骤?
例2:如图,水以常速(即单位时间内注入水的
体积相同)注入下面四种底面积相同的容器中,请分别找出与各容器对应的水的高度h与
时间t的函数关系图象。
h
O
t
h
O
t
h
O
t
h
O
(A)
(B)
(C)
(D)
(1)
(2)
(3)
(4)
【总一总★成竹在胸】
当函数 y=f (x) 在区间 内可导时,
