沪科版数学九年级上册 21.6 综合与实践 获取最大利润 课件 (共14张PPT)
文档属性
| 名称 | 沪科版数学九年级上册 21.6 综合与实践 获取最大利润 课件 (共14张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 105.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-31 09:48:27 | ||
图片预览




文档简介
(共14张PPT)
21.6 综合与实践 获取最大利润
二次函数的一般形式:
=a(x+ )2+
y=ax2+bx+c (a≠0)
复 习 回 顾
建立两个变量之间的函数模型的一般步骤:
1.将实验得到的数据在直角坐标系中描出;
2.观察这些数据的特征,确定选用的函数形式,并根据已知数据求出具体的函数表达式;
3.进行检验;
4.应用这个函数模型解决问题 .
一个制造商制造一种产品,它的成本可以分为固定成本和可变成本两个部分,其中固定成本包括设计产品 建造厂房 购置设备 培训工人等费用,如果没有更换产品,我们将它看为常数;可变成本与该产品生产的件数有关,而每件产品的成本包括劳动力 材料 包装 运输等费用。例如,生产一种收音机的成本(单位:元)可以近似的表述为
其中C表示生产 t台收音机的总成本,当t=0时
C=120t+1000 ①
C成本=120×0+1 000=1 000
1000元是固定成本,由此可知①式中120t表示可变成本
制造商出售产品得到的年总收入等于出售产品的年销售量t和产品的销售单价x的乘积,设R表示年总收入,则
R年总收入=t ·x ②
自主探究
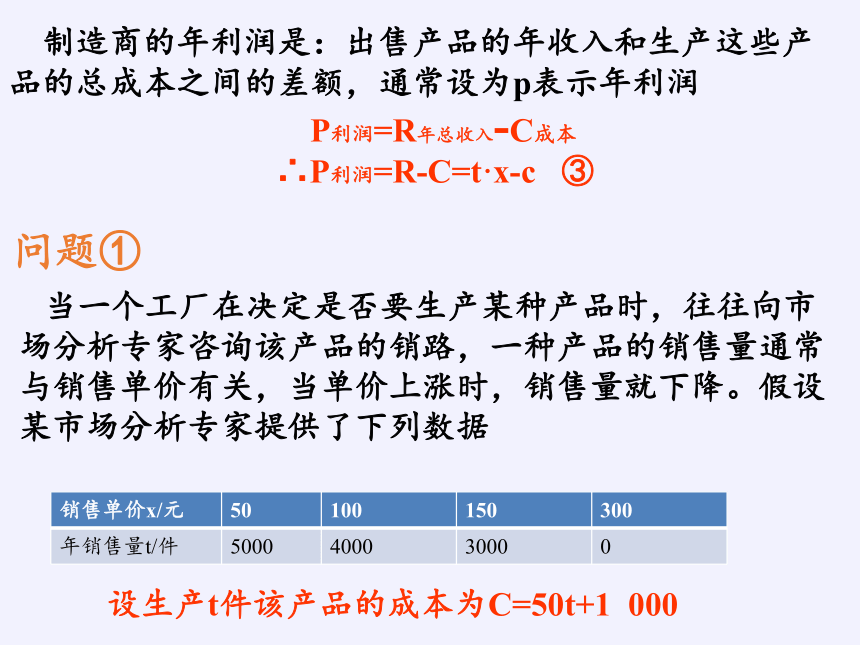
制造商的年利润是:出售产品的年收入和生产这些产品的总成本之间的差额,通常设为p表示年利润
问题①
P利润=R年总收入-C成本
∴P利润=R-C=t·x-c ③
当一个工厂在决定是否要生产某种产品时,往往向市场分析专家咨询该产品的销路,一种产品的销售量通常与销售单价有关,当单价上涨时,销售量就下降。假设某市场分析专家提供了下列数据
销售单价x/元 50 100 150 300
年销售量t/件 5000 4000 3000 0
设生产t件该产品的成本为C=50t+1 000
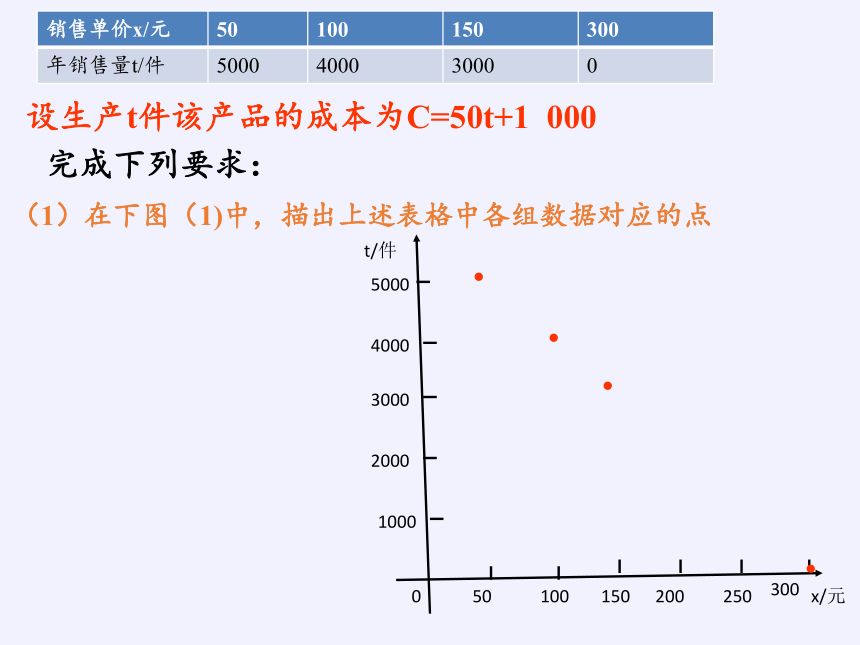
完成下列要求:
(1)在下图(1)中,描出上述表格中各组数据对应的点
销售单价x/元 50 100 150 300
年销售量t/件 5000 4000 3000 0
设生产t件该产品的成本为C=50t+1 000
4000
1000
2000
3000
5000
50
100
150
200
250
300
x/元
t/件
0
·
·
·
·
完成下列要求:
(1)在下图(1)中,描出上述表格中个组数据对应的点
销售单价x/元 50 100 150 300
年销售量t/件 5000 4000 3000 0
设生产t件该产品的成本为C=50t+1 000
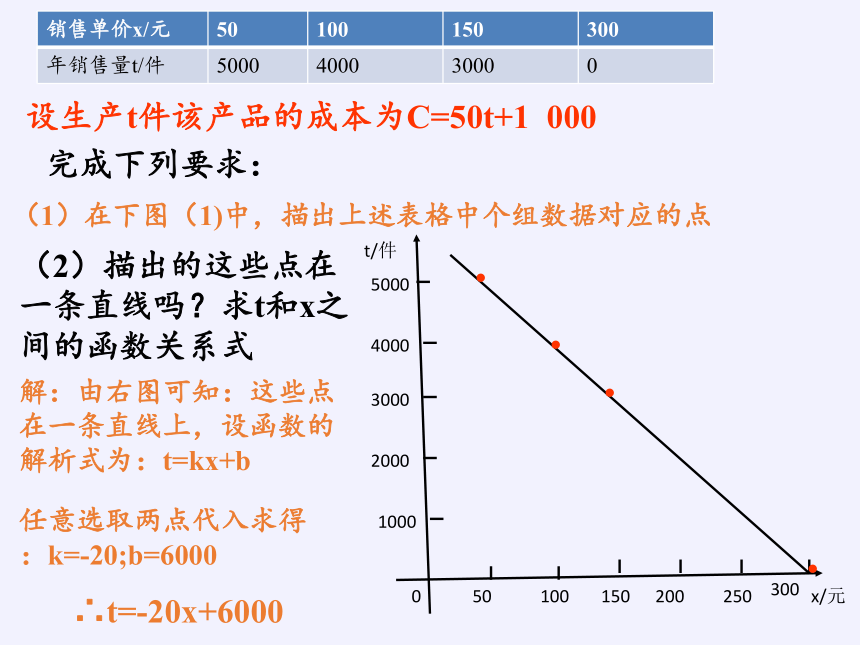
(2)描出的这些点在一条直线吗?求t和x之间的函数关系式
4000
1000
2000
3000
5000
50
100
150
200
250
300
x/元
t/件
0
·
·
·
·
解:由右图可知:这些点在一条直线上,设函数的解析式为:t=kx+b
任意选取两点代入求得:k=-20;b=6000
∴t=-20x+6000
销售单价x/元 50 100 150 300
年销售量t/件 5000 4000 3000 0
设生产t件该产品的成本为C=50t+1 000
(3)销售单价x和年销售量t各为多少时,年利润p最大?
=-20x +6000x-50t-1000
解:∵R年总收入=t ·x
∴R年总收入=(-20x+6000) ·x
∴P利润=R年总收入-C成本=t·x-c
∴P利润=(-20x+6000) ·x -(50t+1 000)
=-20x +6000x-50(-20x+6000)-1000
=-20x +6000x+1000x-300000-1000
=-20x +7000x-301000
由公式可得:当 x= 时 即x=175 p最大 =
P=311500元
∴t=-20x+6000=2500
制造商为了获得最大利润,进行了市场调查,取得了该种电子产品销售单价x和年销售量t之间的一组数据
问题②
年销售量t/件 750 3000 5096 8500 9417
销售单价x/元 3850 3400 3000 2300 2100
t/件
小试牛刀
设生产t件某种电子产品的成本(单位:元)可以近似的表示为:
C=1000t+2 000 000
问题②
C=1000t+2 000 000
(1)在图中,描出上述表格中各组数据对应的点
3500
2000
2500
3000
4000
1000
2000
3000
4000
7000
8000
t/件
x/元
0
5000
6000
9000
10000
·
·
·
·
·
小试牛刀
设生产t件某种电子产品的成本(单位:元)可以近似的表示为:
年销售量t/件 750 3000 5096 8500 9417
销售单价x/元 3850 3400 3000 2300 2100
(2)假如该企业高薪聘你,请你分析,当年销售量t和销售单价x分别是多少时,年利润P最大?并说说你有几种求解方法?与同学进行交流.
设生产t件某种电子产品的成本(单位:元)可以近似的表示为:
年销售量t/件 750 3000 5096 8500 9417
销售单价x/元 3850 3400 3000 2300 2100
C=1000t+2 000 000
问题②
二次函数是一类最优化问题的数学模型,它能帮助我们解决实际生活中如何获取最大利润问题,它来源于生活又服务于生活。
课堂总结
通过本节课学习你有哪些收获?还有哪些疑问?和同伴交流一下学习心得。
必做题:教材p58第11题
选做题:请查阅资料,每位同学寻找一个生活中的实际问题,与同伴交流,让各自的同伴选择一个恰当的函数应用模型解决问题,然后在班级进行展示交流。
布置作业
谢 谢
21.6 综合与实践 获取最大利润
二次函数的一般形式:
=a(x+ )2+
y=ax2+bx+c (a≠0)
复 习 回 顾
建立两个变量之间的函数模型的一般步骤:
1.将实验得到的数据在直角坐标系中描出;
2.观察这些数据的特征,确定选用的函数形式,并根据已知数据求出具体的函数表达式;
3.进行检验;
4.应用这个函数模型解决问题 .
一个制造商制造一种产品,它的成本可以分为固定成本和可变成本两个部分,其中固定成本包括设计产品 建造厂房 购置设备 培训工人等费用,如果没有更换产品,我们将它看为常数;可变成本与该产品生产的件数有关,而每件产品的成本包括劳动力 材料 包装 运输等费用。例如,生产一种收音机的成本(单位:元)可以近似的表述为
其中C表示生产 t台收音机的总成本,当t=0时
C=120t+1000 ①
C成本=120×0+1 000=1 000
1000元是固定成本,由此可知①式中120t表示可变成本
制造商出售产品得到的年总收入等于出售产品的年销售量t和产品的销售单价x的乘积,设R表示年总收入,则
R年总收入=t ·x ②
自主探究
制造商的年利润是:出售产品的年收入和生产这些产品的总成本之间的差额,通常设为p表示年利润
问题①
P利润=R年总收入-C成本
∴P利润=R-C=t·x-c ③
当一个工厂在决定是否要生产某种产品时,往往向市场分析专家咨询该产品的销路,一种产品的销售量通常与销售单价有关,当单价上涨时,销售量就下降。假设某市场分析专家提供了下列数据
销售单价x/元 50 100 150 300
年销售量t/件 5000 4000 3000 0
设生产t件该产品的成本为C=50t+1 000
完成下列要求:
(1)在下图(1)中,描出上述表格中各组数据对应的点
销售单价x/元 50 100 150 300
年销售量t/件 5000 4000 3000 0
设生产t件该产品的成本为C=50t+1 000
4000
1000
2000
3000
5000
50
100
150
200
250
300
x/元
t/件
0
·
·
·
·
完成下列要求:
(1)在下图(1)中,描出上述表格中个组数据对应的点
销售单价x/元 50 100 150 300
年销售量t/件 5000 4000 3000 0
设生产t件该产品的成本为C=50t+1 000
(2)描出的这些点在一条直线吗?求t和x之间的函数关系式
4000
1000
2000
3000
5000
50
100
150
200
250
300
x/元
t/件
0
·
·
·
·
解:由右图可知:这些点在一条直线上,设函数的解析式为:t=kx+b
任意选取两点代入求得:k=-20;b=6000
∴t=-20x+6000
销售单价x/元 50 100 150 300
年销售量t/件 5000 4000 3000 0
设生产t件该产品的成本为C=50t+1 000
(3)销售单价x和年销售量t各为多少时,年利润p最大?
=-20x +6000x-50t-1000
解:∵R年总收入=t ·x
∴R年总收入=(-20x+6000) ·x
∴P利润=R年总收入-C成本=t·x-c
∴P利润=(-20x+6000) ·x -(50t+1 000)
=-20x +6000x-50(-20x+6000)-1000
=-20x +6000x+1000x-300000-1000
=-20x +7000x-301000
由公式可得:当 x= 时 即x=175 p最大 =
P=311500元
∴t=-20x+6000=2500
制造商为了获得最大利润,进行了市场调查,取得了该种电子产品销售单价x和年销售量t之间的一组数据
问题②
年销售量t/件 750 3000 5096 8500 9417
销售单价x/元 3850 3400 3000 2300 2100
t/件
小试牛刀
设生产t件某种电子产品的成本(单位:元)可以近似的表示为:
C=1000t+2 000 000
问题②
C=1000t+2 000 000
(1)在图中,描出上述表格中各组数据对应的点
3500
2000
2500
3000
4000
1000
2000
3000
4000
7000
8000
t/件
x/元
0
5000
6000
9000
10000
·
·
·
·
·
小试牛刀
设生产t件某种电子产品的成本(单位:元)可以近似的表示为:
年销售量t/件 750 3000 5096 8500 9417
销售单价x/元 3850 3400 3000 2300 2100
(2)假如该企业高薪聘你,请你分析,当年销售量t和销售单价x分别是多少时,年利润P最大?并说说你有几种求解方法?与同学进行交流.
设生产t件某种电子产品的成本(单位:元)可以近似的表示为:
年销售量t/件 750 3000 5096 8500 9417
销售单价x/元 3850 3400 3000 2300 2100
C=1000t+2 000 000
问题②
二次函数是一类最优化问题的数学模型,它能帮助我们解决实际生活中如何获取最大利润问题,它来源于生活又服务于生活。
课堂总结
通过本节课学习你有哪些收获?还有哪些疑问?和同伴交流一下学习心得。
必做题:教材p58第11题
选做题:请查阅资料,每位同学寻找一个生活中的实际问题,与同伴交流,让各自的同伴选择一个恰当的函数应用模型解决问题,然后在班级进行展示交流。
布置作业
谢 谢
