人教版八年级数学上册《第十五章章末复习》名师教案
文档属性
| 名称 | 人教版八年级数学上册《第十五章章末复习》名师教案 | 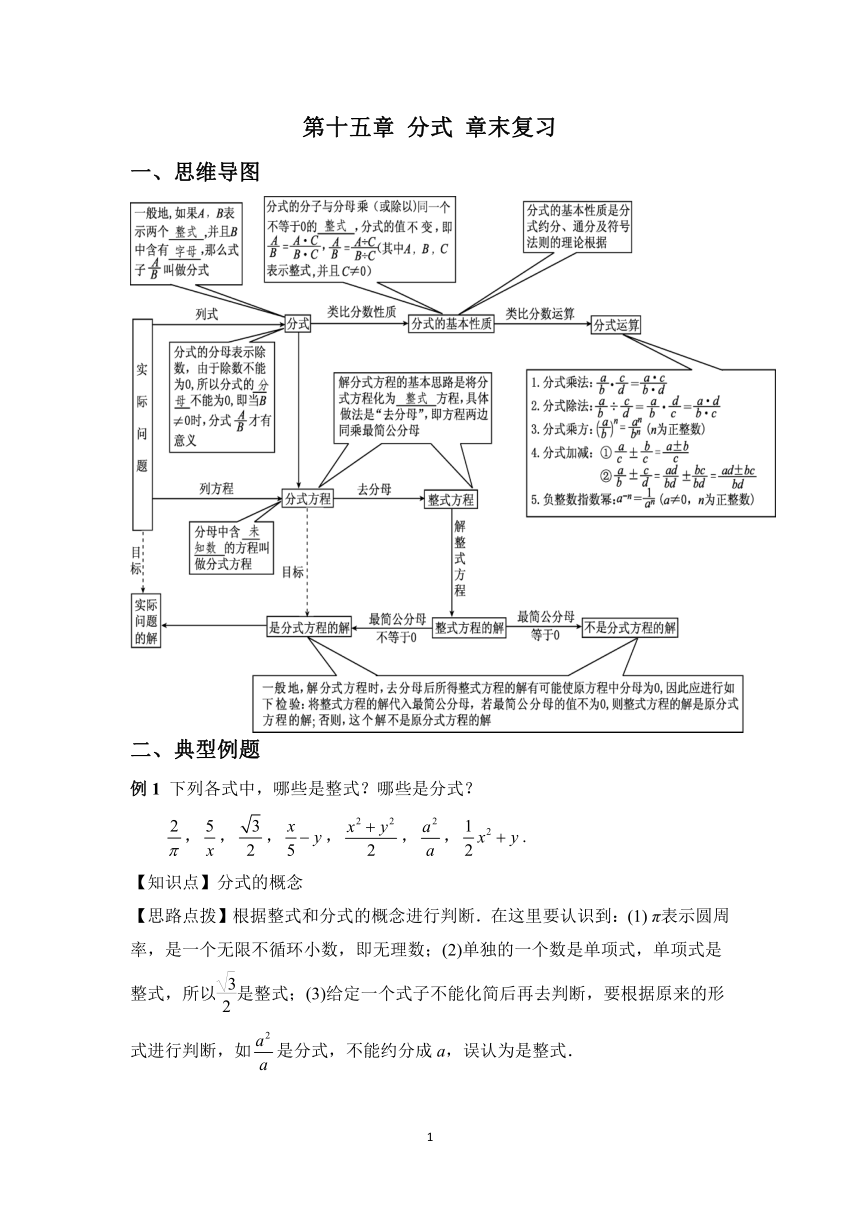 | |
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-31 09:58:42 | ||
图片预览





文档简介
第十五章 分式 章末复习
一、思维导图
INCLUDEPICTURE "D:\\vcomDownload\\RJB3.TIF" \* MERGEFORMAT INCLUDEPICTURE "D:\\..\\..\\..\\..\\..\\acer\\Desktop\\RJB3.TIF" \* MERGEFORMAT INCLUDEPICTURE "D:\\..\\..\\..\\..\\..\\acer\\Desktop\\RJB3.TIF" \* MERGEFORMAT INCLUDEPICTURE "D:\\..\\..\\..\\..\\..\\acer\\Desktop\\RJB3.TIF" \* MERGEFORMAT INCLUDEPICTURE "D:\\..\\..\\..\\..\\..\\acer\\Desktop\\RJB3.TIF" \* MERGEFORMAT INCLUDEPICTURE "D:\\..\\..\\..\\..\\..\\acer\\Desktop\\RJB3.TIF" \* MERGEFORMAT INCLUDEPICTURE "D:\\..\\..\\..\\..\\..\\acer\\Desktop\\RJB3.TIF" \* MERGEFORMAT INCLUDEPICTURE "E:\\2016\\玖学堂产品\\上册\\八上第15章分式\\RJB3.TIF" \* MERGEFORMATINET INCLUDEPICTURE "E:\\2016\\玖学堂产品\\上册\\八上第15章分式\\RJB3.TIF" \* MERGEFORMATINET
二、典型例题
例1 下列各式中,哪些是整式?哪些是分式?
,,,,,,.
【知识点】分式的概念
【思路点拨】根据整式和分式的概念进行判断.在这里要认识到:(1) π表示圆周率,是一个无限不循环小数,即无理数;(2)单独的一个数是单项式,单项式是整式,所以是整式;(3)给定一个式子不能化简后再去判断,要根据原来的形式进行判断,如是分式,不能约分成a,误认为是整式.
【解答过程】解:整式有,,,,;分式有,.
例2 计算:(1) ;
(2) ;
(3) .
【知识点】分式的运算
【思路点拨】(1)因为b-a=-(a-b),而1=,所以通分时最简公分母为a-b,也可首先把前两项进行运算.(2)把最后一个分式化简后再进行混合运算.(3)可把y+2视作一个整体,首先进行括号内的运算,再进行括号外的运算.
【解答过程】解:(1)原式===
==2.
或者原式===1+1=2.
(2)原式==
====-1.
(3)原式==
===.
例3 解下列分式方程:
(1) ; (2) .
【知识点】分式方程的解法
【数学思想】化归思想
【思路点拨】 (1)方程中分母x2-1=(x+1)(x-1),所以方程两边同乘最简公分母(x+1)(x-1),注意不含分母的常数项1也要乘(x+1)(x-1);(2)中方程的分母6x-2=2(3x-1),又因为1-3x=-(3x-1),所以方程两边同乘最简公分母2(3x-1),注意常数项也要乘2(3x-1).
【解答过程】解:(1)方程两边同乘(x+1)(x-1),得
x(x+1)-2=(x+1)(x-1).
去括号,得x2+x-2=x2-1.
移项、合并同类项,得x=1.
检验:当x=1时,(x+1)(x-1)=0,所以原分式方程无解.
(2)原方程化为
方程两边同乘2(3x-1),得1=(3x-1)-4.
解得x=2.
检验:当x=2时,2(3x-1)≠0,所以x=2是原分式方程的解.
例4 甲、乙两车间生产同一种零件,乙车间比甲车间平均每小时多生产30个,甲车间生产600个零件与乙车间生产900个零件所用时间相等,设甲车间平均每小时生产x个零件,请按要求解决下列问题:
(1)根据题意,填写下表:
车间 生产零件总个数 平均每小时生产零件的个数 所用时间
甲车间 600 x
乙车间 900 ________ ________
(2)甲、乙两车间平均每小时各生产多少个零件?
【知识点】分式方程的应用
【数学思想】转化思想
【思路点拨】 先用x表示乙车间平均每小时生产的零件个数,再用x表示乙车间生产900个零件所用的时间,根据“时间相等”列方程.
【解答过程】解:(1)依次填入30+x,.
(2)依题意列方程,得,
解得x=60,30+x=90.
当x=60时,x与30+x均不为0,且符合实际意义.
所以甲车间平均每小时生产60个零件,乙车间平均每小时生产90个零件.
三、章末检测题
(一)选择题:
1. 下列各式:其中分式共有( )
A.1个 B.2个 C.3个 D.4个
【知识点】分式的定义
【思路点拨】依据分式的概念进行判断.
【解答过程】都是整式,是分式.故选A.
【答案】A
2. 若分式的值为0,则x的值为( )
A.2或-1 B.0 C.2 D.-1
【知识点】分式的有关概念
【思路点拨】分式的值为0,则分子为0而分母不为0.
【解答过程】由题意可知x-2=0,得x=2.由x+1≠0,得x≠-1,所以x=2,故选C.
【答案】C
3.分式可变形为( )
A. B. C. D.
【知识点】分式的基本性质
【思路点拨】分子、分母、分式本身的符号,只要同时改变其中的两个,分式的值不变.
【答案】D
4.若x、y的值均扩大为原来的2倍,则下列分式的值保持不变的是( )
A. B. C. D.
【知识点】分式的基本性质
【思路点拨】 .
【解答过程】
【答案】A
5. 下列约分正确的是( )
A. B.
C. D.
【知识点】分式的基本性质
【思路点拨】分式的分子、分母除以同一个不等于0的整式,分式的值不变.
【答案】C
6.计算的正确结果是( )
A.0 B. C. D.
【知识点】分式的通分
【思路点拨】最简公分母为,通分可得.
【解答过程】== =
【答案】C
7.下列计算正确的是( )
A. B. C. D.
【知识点】分式的运算
【思路点拨】运用分式的加、减、乘、除的运算法则进行检查.
【解答过程】,则A错误的;,则B错误的;,则C错误的;是正确的;故选D.
【答案】D
8.下列分式中,最简分式是( )
A. B. C. D.
【知识点】最简分式
【思路点拨】利用最简分式的定义判断即可.
【解答过程】解:A原式为最简分式,符合题意;B原式==,不合题意;C原式==,不合题意;D原式==,不合题意,故选A
【答案】A
9.解分式方程时,去分母后变形正确的为( )
A.2+(x+2)=3(x-1) B.2-x+2=3(x-1)
C.2-(x+2)=3 D.2-(x+2)=3(x-1)
【知识点】分式方程的解法
【数学思想】化归思想
【思路点拨】两边都乘以x-1可得结果.
【解答过程】原方程可化为,在方程的两边同乘以(x-1),得2-(x+2)=3(x-1),故选D.
【答案】D
10.A、B两地相距160千米,甲车和乙车的平均速度之比为4∶5,两车同时从A地出发到B地,乙车比甲车早到30分钟,若求甲车的平均速度,设甲车平均速度为4x千米/小时,则所列方程是( )
A. B. C. D.
【知识点】分式方程的应用
【数学思想】转化思想
【思路点拨】设甲车平均速度为4x千米/小时,则乙车平均速度为5x千米/小时,根据两车同时从A地出发到B地,乙车比甲车早到30分钟列出方程即可.
【解答过程】解:设甲车平均速度为4x千米/小时,则乙车平均速度为5x千米/小时,根据题意得,.故选B.
【答案】B
11.若关于x的分式方程的解为非负数,则m的取值范围是( )
A.m>-1 B.m≥-1 C.m>-1且m≠1 D.m≥-1且m≠1
【知识点】分式方程的解、分式方程的解法
【数学思想】转化思想
【思路点拨】此题解题的关键是用关于m的式子表示出分式方程的解;先对原分式方程去分母转化为整式方程,可用含m的代数式表示出x=;又由于该分式方程的解为非负数,于是可以得出关于m的不等式,从而求出m的值;
又根据已知分式方程可知x-1≠0,则有≠1,对其求解得到m不能取到的值,即可使问题得解.
【解答过程】方程两边都乘以(x-1),得m-1=2(x-1),所以x=.
∵x为非负数,∴ ≥0.解得m≥-1.
又∵x-1≠0,即≠1,∴m≠1,故选D.
【答案】D.
12.小明骑自行车沿公路以akm/h的速度行走全程的一半,又以bkm/h的速度行走余下的一半路程;小刚骑自行车以akm/h的速度走全程时间的一半,又以bkm/h的速度行走另一半时间(),则谁走完全程所用的时间较少?( )
A.小明 B.小刚 C.时间相同 D.无法确定
【知识点】分式的应用
【数学思想】转化思想
【思路点拨】把全程看作单位“1”.根据时间=路程÷速度,表示出小明、小刚所用的总时间;为了比较它们的大小,用做差法,看差的正负性.
【解答过程】解:设全程为1,小明所用总时间是=,小刚所用总时间是,小明所用时间减去小刚所用时间得-==>0,显然小刚所用的时间较少.故选B
【答案】B
(二)填空题:
13. 当式子有意义时,x应满足的条件为________.
【知识点】分式有意义
【思路点拨】分式有意义的条件是分母不能为0.
【解答过程】解:∵分母不能为0,∴,即,则x≠±1.
【答案】x≠±1.
14. 杨絮纤维的直径约为0.0000105 m,该直径用科学记数法表示为________.
【知识点】科学记数法
【思路点拨】绝对值小于1的数可以用科学记数法表示为.
【解答过程】0.0000105= 1.05×10-5
【答案】1.05×10-5
15. 关于x的分式方程无解,则m=___.
【知识点】分式方程的解
【数学思想】化归思想、分类思想.
【思路点拨】分式方程无解的条件是:去分母后所得整式方程无解,或解这个整式方程得到的解使原方程的分母等于0.
【解答过程】方程去分母得:m (x 2)=0,解得:x=2+m,
∴当x=2时分母为0,方程无解,
即2+m=2,∴m=0时方程无解.
当x= 2时分母为0,方程无解,
即2+m= 2,∴m= 4时方程无解.
综上所述,m的值是0或 4.
【答案】0或 4.
16.若,则__________.
【知识点】分式的性质
【数学思想】整体思想
【思路点拨】先对所求代数式化简,再把的值整体代入求值即可.或先把 两边同时平方,求出的值,然后对所求代数式化简,再把的值整体代入求值即可.
【解答过程】方法一:=;
∴当,原式=32 1=8.
方法二:由得,,∴=.
【答案】8.
17. 如果实数x,y是方程组的解,那么式子 的值为______.
【知识点】分式的值
【思路点拨】先求出方程组的解得到x与y的值,再把原式括号中两项通分并利用同分母分式的加法法则计算,同时利用除法法则变形,约分得到最简结果,最后代入计算即可求出值.
【解答过程】解:解方程组得 ∴ 原式==xy+2(x+y)=3×(-1)+2×(3-1)=-3+4=1.
【答案】1.
18. 已知三个数x、y、z满足,,,则的值为___.
【知识点】分式的化简求值
【数学思想】转化思想
【思路点拨】所求式子分子分母除以xyz变形后,将已知三等式左边变形后代入,计算即可求出值.
【解答过程】∵,,
∴,,,
∴ 即:,
则=, ∴= 4
【答案】 4
(三)解答题:
19.化简:(1) ;(2) .
【知识点】分式的混合运算
【思路点拨】运用分式的加、减、乘、除运算法则进行运算.
【解答过程】解:(1)原式=
==.
(2)原式===.
20.解下列分式方程:
(1) ; (2) .
【知识点】分式方程的解法.
【数学思想】化归思想.
【思路点拨】去分母,把分式方程转化为整式方程,再解整式方程,最后检验.
【解答过程】解:(1)去分母得x=2(3x-1)+1,去括号得x=6x-2+1,合并同类项得5x=1,系数化为1得x=. 经检验,x=是分式方程的解.
(2)原方程可化为,
两边同时乘以(2x+1)(2x-1),得
x+1=3(2x-1)-2(2x+1),
x+1=6x-3-4x-2,
解得x=6.
经检验,x=6是原分式方程的解.
∴原方程的解是x=6.
21.先化简,再求值:已知,求的值.
【知识点】分式的运算
【数学思想】整体思想
【思路点拨】先利用分式的运算法则化简,再代入求值.
【解答过程】原式==
===,
当时,原式===
22.某校学生利用双休时间去距学校10km的炎帝故里参观,一部分学生骑自行车先走,过了20min后,其余学生乘汽车沿相同路线出发,结果他们同时到达.已知汽车的速度是骑车学生速度的2倍,求骑车学生的速度和汽车的速度.
【知识点】分式方程的应用.
【数学思想】转化思想
【思路点拨】求速度,路程已知,根据时间来列等量关系.关键描述语为:“一部分学生骑自行车先走,过了20min后,其余学生乘汽车沿相同路线出发,结果他们同时到达”,根据等量关系列出方程.
【解答过程】解:设骑车学生的速度为x千米/小时,汽车的速度为2x千米/小时,
可得:,
解得:x=15,
经检验:x=15是原方程的解,
2x=2×15=30,
答:骑车学生的速度和汽车的速度分别是每小时15km,30km.
23.某市为创建全国文明城市,开展“美化绿化城市”活动,计划经过若干年使城区绿化总面积新增360万平方米.自2013年初开始实施后,实际每年绿化面积是原计划的1.6倍,这样可提前4年完成任务.
(1)问实际每年绿化面积多少万平方米?
(2)为加大创城力度,市政府决定从2016年起加快绿化速度,要求不超过2年完成,那么实际平均每年绿化面积至少还要增加多少万平方米?
【知识点】分式方程的应用、一元一次不等式的应用.
【数学思想】化归思想
【思路点拨】(1)设原计划每年绿化面积为x万平方米,则实际每年绿化面积为1.6x万平方米.根据“实际每年绿化面积是原计划的1.6倍,这样可提前4年完成任务”列出方程,解方程即可;(2)设平均每年绿化面积还要增加a万平方米.则由“完成新增绿化面积不超过2年”列出不等式,解不等式即可.
【解答过程】解:(1)设原计划每年绿化面积为x万平方米,则实际每年绿化面积为1.6x万平方米,根据题意,得
解得:x=33.75,
经检验x=33.75是原分式方程的解,
则1.6x=1.6×33.75=54(万平方米).
答:实际每年绿化面积为54万平方米;
(2)设平均每年绿化面积还要增加a万平方米,根据题意,得
54×3+2(54+a)≥360
解得:a≥45.
答:实际平均每年绿化面积至少还要增加45万平方米.
24.已知a为大于2的整数,若关于x的不等式组无解.
(1)求a的值;
(2)化简并求的值.
【知识点】分式的混合运算、不等式组的解集
【思路点拨】先求出不等式组的解集,根据无解得出a的值,再化简求值.
【解答过程】解:(1)解不等式2x-a≤0,得x≤.
∵原不等式组无解,∴<2,解得a<4.
又∵a为大于2的整数,∴a=3.
(2)原式===a+1.
当a=3时,原式=3+1=4.
25.某校原有600张旧课桌急需维修,经过A、B、C三个工程队的竞标得知,A、B工程队的工作效率相同,且都为C工程队的2倍,若由一个工程队单独完成,C工程队比A工程队要多用10天.学校决定由三个工程队一起施工,要求至多6天完成维修任务.三个工程队都按原来的工作效率施工2天后,学校又清理出需要维修的课桌360张,为了不超过6天时限,工程队决定从第3天开始,各自都提高工作效率,A、B工程队提高的工作效率仍然都是C工程队提高的2倍,这样他们至少还需要3天才能完成整个维修任务.
(1)求A工程队原来平均每天维修课桌的张数;
(2)求A工程队提高工作效率后平均每天多维修的课桌张数a的取值范围.
【知识点】分式方程的应用、不等式的应用
【数学思想】转化思想
【思路点拨】(1)求工效,有工作总量,应根据时间来列等量关系为:C队所用天数-A队所用天数=10;
(2)剩余任务完成的天数应在3天和4天之间.
【解答过程】解:(1)设C工程队原来平均每天维修课桌x张,
根据题意,得.
解这个方程,得x=30.
经检验,x=30是原方程的根,且符合题意,2x=60.
答:A工程队原来平均每天维修课桌60张.
(2)设C工程队提高工作效率后平均每天多维修课桌y张,施工2天后,已维修(60+60+30)×2=300(张), 从第3天起还需维修的张数应为600-300+360=660(张).
根据题意,得3(2y+2y+y+150)≤660≤4(2y+2y+y+150).
解这个不等式组,得3≤y≤14.
∴6≤2y≤28.
答:A工程队提高工作效率后平均每天多维修的课桌张数a的取值范围为6≤a≤28.
26.阅读下面材料,并解答问题.
材料:将分式拆分成一个整式与一个分式(分子为整数)的和的形式.
解:由分母为 x2+1,可设 x4 x2+3=( x2+1)(x2+a)+b
则 x4 x2+3=( x2+1)(x2+a)+b= x4 ax2+x2+a+b= x4 (a 1)x2+(a+b)
∵对应任意x,上述等式均成立,∴,∴a=2,b=1.
∴===
这样,分式被拆分成了一个整式与一个分式的和。
解答:
(1)请你仿照上述过程将分式拆分成一个整式与一个分式(分子为
整数)的和的形式.
(2)当时,试说明的最小值为8.
【知识点】分式的混合运算
【数学思想】整体思想
【思路点拨】只需仿照原材料中的解题过程就可解决问题.
【解答过程】解:(1)由分母为 x2+1,可设 x4 6x2+8=( x2+1)(x2+a)+b
则 x4 6x2+8=( x2+1)(x2+a)+b= x4 ax2+x2+a+b= x4 (a 1)x2+(a+b)
∵对应任意x,上述等式均成立,∴,∴a=7,b=1.
∴===
这样,分式被拆分成了一个整式与一个分式的和.
(2)当时,由=知,对于,
当x=0时,这两个式子的和有最小值,最小值为8,
即的最小值为8.
一、思维导图
INCLUDEPICTURE "D:\\vcomDownload\\RJB3.TIF" \* MERGEFORMAT INCLUDEPICTURE "D:\\..\\..\\..\\..\\..\\acer\\Desktop\\RJB3.TIF" \* MERGEFORMAT INCLUDEPICTURE "D:\\..\\..\\..\\..\\..\\acer\\Desktop\\RJB3.TIF" \* MERGEFORMAT INCLUDEPICTURE "D:\\..\\..\\..\\..\\..\\acer\\Desktop\\RJB3.TIF" \* MERGEFORMAT INCLUDEPICTURE "D:\\..\\..\\..\\..\\..\\acer\\Desktop\\RJB3.TIF" \* MERGEFORMAT INCLUDEPICTURE "D:\\..\\..\\..\\..\\..\\acer\\Desktop\\RJB3.TIF" \* MERGEFORMAT INCLUDEPICTURE "D:\\..\\..\\..\\..\\..\\acer\\Desktop\\RJB3.TIF" \* MERGEFORMAT INCLUDEPICTURE "E:\\2016\\玖学堂产品\\上册\\八上第15章分式\\RJB3.TIF" \* MERGEFORMATINET INCLUDEPICTURE "E:\\2016\\玖学堂产品\\上册\\八上第15章分式\\RJB3.TIF" \* MERGEFORMATINET
二、典型例题
例1 下列各式中,哪些是整式?哪些是分式?
,,,,,,.
【知识点】分式的概念
【思路点拨】根据整式和分式的概念进行判断.在这里要认识到:(1) π表示圆周率,是一个无限不循环小数,即无理数;(2)单独的一个数是单项式,单项式是整式,所以是整式;(3)给定一个式子不能化简后再去判断,要根据原来的形式进行判断,如是分式,不能约分成a,误认为是整式.
【解答过程】解:整式有,,,,;分式有,.
例2 计算:(1) ;
(2) ;
(3) .
【知识点】分式的运算
【思路点拨】(1)因为b-a=-(a-b),而1=,所以通分时最简公分母为a-b,也可首先把前两项进行运算.(2)把最后一个分式化简后再进行混合运算.(3)可把y+2视作一个整体,首先进行括号内的运算,再进行括号外的运算.
【解答过程】解:(1)原式===
==2.
或者原式===1+1=2.
(2)原式==
====-1.
(3)原式==
===.
例3 解下列分式方程:
(1) ; (2) .
【知识点】分式方程的解法
【数学思想】化归思想
【思路点拨】 (1)方程中分母x2-1=(x+1)(x-1),所以方程两边同乘最简公分母(x+1)(x-1),注意不含分母的常数项1也要乘(x+1)(x-1);(2)中方程的分母6x-2=2(3x-1),又因为1-3x=-(3x-1),所以方程两边同乘最简公分母2(3x-1),注意常数项也要乘2(3x-1).
【解答过程】解:(1)方程两边同乘(x+1)(x-1),得
x(x+1)-2=(x+1)(x-1).
去括号,得x2+x-2=x2-1.
移项、合并同类项,得x=1.
检验:当x=1时,(x+1)(x-1)=0,所以原分式方程无解.
(2)原方程化为
方程两边同乘2(3x-1),得1=(3x-1)-4.
解得x=2.
检验:当x=2时,2(3x-1)≠0,所以x=2是原分式方程的解.
例4 甲、乙两车间生产同一种零件,乙车间比甲车间平均每小时多生产30个,甲车间生产600个零件与乙车间生产900个零件所用时间相等,设甲车间平均每小时生产x个零件,请按要求解决下列问题:
(1)根据题意,填写下表:
车间 生产零件总个数 平均每小时生产零件的个数 所用时间
甲车间 600 x
乙车间 900 ________ ________
(2)甲、乙两车间平均每小时各生产多少个零件?
【知识点】分式方程的应用
【数学思想】转化思想
【思路点拨】 先用x表示乙车间平均每小时生产的零件个数,再用x表示乙车间生产900个零件所用的时间,根据“时间相等”列方程.
【解答过程】解:(1)依次填入30+x,.
(2)依题意列方程,得,
解得x=60,30+x=90.
当x=60时,x与30+x均不为0,且符合实际意义.
所以甲车间平均每小时生产60个零件,乙车间平均每小时生产90个零件.
三、章末检测题
(一)选择题:
1. 下列各式:其中分式共有( )
A.1个 B.2个 C.3个 D.4个
【知识点】分式的定义
【思路点拨】依据分式的概念进行判断.
【解答过程】都是整式,是分式.故选A.
【答案】A
2. 若分式的值为0,则x的值为( )
A.2或-1 B.0 C.2 D.-1
【知识点】分式的有关概念
【思路点拨】分式的值为0,则分子为0而分母不为0.
【解答过程】由题意可知x-2=0,得x=2.由x+1≠0,得x≠-1,所以x=2,故选C.
【答案】C
3.分式可变形为( )
A. B. C. D.
【知识点】分式的基本性质
【思路点拨】分子、分母、分式本身的符号,只要同时改变其中的两个,分式的值不变.
【答案】D
4.若x、y的值均扩大为原来的2倍,则下列分式的值保持不变的是( )
A. B. C. D.
【知识点】分式的基本性质
【思路点拨】 .
【解答过程】
【答案】A
5. 下列约分正确的是( )
A. B.
C. D.
【知识点】分式的基本性质
【思路点拨】分式的分子、分母除以同一个不等于0的整式,分式的值不变.
【答案】C
6.计算的正确结果是( )
A.0 B. C. D.
【知识点】分式的通分
【思路点拨】最简公分母为,通分可得.
【解答过程】== =
【答案】C
7.下列计算正确的是( )
A. B. C. D.
【知识点】分式的运算
【思路点拨】运用分式的加、减、乘、除的运算法则进行检查.
【解答过程】,则A错误的;,则B错误的;,则C错误的;是正确的;故选D.
【答案】D
8.下列分式中,最简分式是( )
A. B. C. D.
【知识点】最简分式
【思路点拨】利用最简分式的定义判断即可.
【解答过程】解:A原式为最简分式,符合题意;B原式==,不合题意;C原式==,不合题意;D原式==,不合题意,故选A
【答案】A
9.解分式方程时,去分母后变形正确的为( )
A.2+(x+2)=3(x-1) B.2-x+2=3(x-1)
C.2-(x+2)=3 D.2-(x+2)=3(x-1)
【知识点】分式方程的解法
【数学思想】化归思想
【思路点拨】两边都乘以x-1可得结果.
【解答过程】原方程可化为,在方程的两边同乘以(x-1),得2-(x+2)=3(x-1),故选D.
【答案】D
10.A、B两地相距160千米,甲车和乙车的平均速度之比为4∶5,两车同时从A地出发到B地,乙车比甲车早到30分钟,若求甲车的平均速度,设甲车平均速度为4x千米/小时,则所列方程是( )
A. B. C. D.
【知识点】分式方程的应用
【数学思想】转化思想
【思路点拨】设甲车平均速度为4x千米/小时,则乙车平均速度为5x千米/小时,根据两车同时从A地出发到B地,乙车比甲车早到30分钟列出方程即可.
【解答过程】解:设甲车平均速度为4x千米/小时,则乙车平均速度为5x千米/小时,根据题意得,.故选B.
【答案】B
11.若关于x的分式方程的解为非负数,则m的取值范围是( )
A.m>-1 B.m≥-1 C.m>-1且m≠1 D.m≥-1且m≠1
【知识点】分式方程的解、分式方程的解法
【数学思想】转化思想
【思路点拨】此题解题的关键是用关于m的式子表示出分式方程的解;先对原分式方程去分母转化为整式方程,可用含m的代数式表示出x=;又由于该分式方程的解为非负数,于是可以得出关于m的不等式,从而求出m的值;
又根据已知分式方程可知x-1≠0,则有≠1,对其求解得到m不能取到的值,即可使问题得解.
【解答过程】方程两边都乘以(x-1),得m-1=2(x-1),所以x=.
∵x为非负数,∴ ≥0.解得m≥-1.
又∵x-1≠0,即≠1,∴m≠1,故选D.
【答案】D.
12.小明骑自行车沿公路以akm/h的速度行走全程的一半,又以bkm/h的速度行走余下的一半路程;小刚骑自行车以akm/h的速度走全程时间的一半,又以bkm/h的速度行走另一半时间(),则谁走完全程所用的时间较少?( )
A.小明 B.小刚 C.时间相同 D.无法确定
【知识点】分式的应用
【数学思想】转化思想
【思路点拨】把全程看作单位“1”.根据时间=路程÷速度,表示出小明、小刚所用的总时间;为了比较它们的大小,用做差法,看差的正负性.
【解答过程】解:设全程为1,小明所用总时间是=,小刚所用总时间是,小明所用时间减去小刚所用时间得-==>0,显然小刚所用的时间较少.故选B
【答案】B
(二)填空题:
13. 当式子有意义时,x应满足的条件为________.
【知识点】分式有意义
【思路点拨】分式有意义的条件是分母不能为0.
【解答过程】解:∵分母不能为0,∴,即,则x≠±1.
【答案】x≠±1.
14. 杨絮纤维的直径约为0.0000105 m,该直径用科学记数法表示为________.
【知识点】科学记数法
【思路点拨】绝对值小于1的数可以用科学记数法表示为.
【解答过程】0.0000105= 1.05×10-5
【答案】1.05×10-5
15. 关于x的分式方程无解,则m=___.
【知识点】分式方程的解
【数学思想】化归思想、分类思想.
【思路点拨】分式方程无解的条件是:去分母后所得整式方程无解,或解这个整式方程得到的解使原方程的分母等于0.
【解答过程】方程去分母得:m (x 2)=0,解得:x=2+m,
∴当x=2时分母为0,方程无解,
即2+m=2,∴m=0时方程无解.
当x= 2时分母为0,方程无解,
即2+m= 2,∴m= 4时方程无解.
综上所述,m的值是0或 4.
【答案】0或 4.
16.若,则__________.
【知识点】分式的性质
【数学思想】整体思想
【思路点拨】先对所求代数式化简,再把的值整体代入求值即可.或先把 两边同时平方,求出的值,然后对所求代数式化简,再把的值整体代入求值即可.
【解答过程】方法一:=;
∴当,原式=32 1=8.
方法二:由得,,∴=.
【答案】8.
17. 如果实数x,y是方程组的解,那么式子 的值为______.
【知识点】分式的值
【思路点拨】先求出方程组的解得到x与y的值,再把原式括号中两项通分并利用同分母分式的加法法则计算,同时利用除法法则变形,约分得到最简结果,最后代入计算即可求出值.
【解答过程】解:解方程组得 ∴ 原式==xy+2(x+y)=3×(-1)+2×(3-1)=-3+4=1.
【答案】1.
18. 已知三个数x、y、z满足,,,则的值为___.
【知识点】分式的化简求值
【数学思想】转化思想
【思路点拨】所求式子分子分母除以xyz变形后,将已知三等式左边变形后代入,计算即可求出值.
【解答过程】∵,,
∴,,,
∴ 即:,
则=, ∴= 4
【答案】 4
(三)解答题:
19.化简:(1) ;(2) .
【知识点】分式的混合运算
【思路点拨】运用分式的加、减、乘、除运算法则进行运算.
【解答过程】解:(1)原式=
==.
(2)原式===.
20.解下列分式方程:
(1) ; (2) .
【知识点】分式方程的解法.
【数学思想】化归思想.
【思路点拨】去分母,把分式方程转化为整式方程,再解整式方程,最后检验.
【解答过程】解:(1)去分母得x=2(3x-1)+1,去括号得x=6x-2+1,合并同类项得5x=1,系数化为1得x=. 经检验,x=是分式方程的解.
(2)原方程可化为,
两边同时乘以(2x+1)(2x-1),得
x+1=3(2x-1)-2(2x+1),
x+1=6x-3-4x-2,
解得x=6.
经检验,x=6是原分式方程的解.
∴原方程的解是x=6.
21.先化简,再求值:已知,求的值.
【知识点】分式的运算
【数学思想】整体思想
【思路点拨】先利用分式的运算法则化简,再代入求值.
【解答过程】原式==
===,
当时,原式===
22.某校学生利用双休时间去距学校10km的炎帝故里参观,一部分学生骑自行车先走,过了20min后,其余学生乘汽车沿相同路线出发,结果他们同时到达.已知汽车的速度是骑车学生速度的2倍,求骑车学生的速度和汽车的速度.
【知识点】分式方程的应用.
【数学思想】转化思想
【思路点拨】求速度,路程已知,根据时间来列等量关系.关键描述语为:“一部分学生骑自行车先走,过了20min后,其余学生乘汽车沿相同路线出发,结果他们同时到达”,根据等量关系列出方程.
【解答过程】解:设骑车学生的速度为x千米/小时,汽车的速度为2x千米/小时,
可得:,
解得:x=15,
经检验:x=15是原方程的解,
2x=2×15=30,
答:骑车学生的速度和汽车的速度分别是每小时15km,30km.
23.某市为创建全国文明城市,开展“美化绿化城市”活动,计划经过若干年使城区绿化总面积新增360万平方米.自2013年初开始实施后,实际每年绿化面积是原计划的1.6倍,这样可提前4年完成任务.
(1)问实际每年绿化面积多少万平方米?
(2)为加大创城力度,市政府决定从2016年起加快绿化速度,要求不超过2年完成,那么实际平均每年绿化面积至少还要增加多少万平方米?
【知识点】分式方程的应用、一元一次不等式的应用.
【数学思想】化归思想
【思路点拨】(1)设原计划每年绿化面积为x万平方米,则实际每年绿化面积为1.6x万平方米.根据“实际每年绿化面积是原计划的1.6倍,这样可提前4年完成任务”列出方程,解方程即可;(2)设平均每年绿化面积还要增加a万平方米.则由“完成新增绿化面积不超过2年”列出不等式,解不等式即可.
【解答过程】解:(1)设原计划每年绿化面积为x万平方米,则实际每年绿化面积为1.6x万平方米,根据题意,得
解得:x=33.75,
经检验x=33.75是原分式方程的解,
则1.6x=1.6×33.75=54(万平方米).
答:实际每年绿化面积为54万平方米;
(2)设平均每年绿化面积还要增加a万平方米,根据题意,得
54×3+2(54+a)≥360
解得:a≥45.
答:实际平均每年绿化面积至少还要增加45万平方米.
24.已知a为大于2的整数,若关于x的不等式组无解.
(1)求a的值;
(2)化简并求的值.
【知识点】分式的混合运算、不等式组的解集
【思路点拨】先求出不等式组的解集,根据无解得出a的值,再化简求值.
【解答过程】解:(1)解不等式2x-a≤0,得x≤.
∵原不等式组无解,∴<2,解得a<4.
又∵a为大于2的整数,∴a=3.
(2)原式===a+1.
当a=3时,原式=3+1=4.
25.某校原有600张旧课桌急需维修,经过A、B、C三个工程队的竞标得知,A、B工程队的工作效率相同,且都为C工程队的2倍,若由一个工程队单独完成,C工程队比A工程队要多用10天.学校决定由三个工程队一起施工,要求至多6天完成维修任务.三个工程队都按原来的工作效率施工2天后,学校又清理出需要维修的课桌360张,为了不超过6天时限,工程队决定从第3天开始,各自都提高工作效率,A、B工程队提高的工作效率仍然都是C工程队提高的2倍,这样他们至少还需要3天才能完成整个维修任务.
(1)求A工程队原来平均每天维修课桌的张数;
(2)求A工程队提高工作效率后平均每天多维修的课桌张数a的取值范围.
【知识点】分式方程的应用、不等式的应用
【数学思想】转化思想
【思路点拨】(1)求工效,有工作总量,应根据时间来列等量关系为:C队所用天数-A队所用天数=10;
(2)剩余任务完成的天数应在3天和4天之间.
【解答过程】解:(1)设C工程队原来平均每天维修课桌x张,
根据题意,得.
解这个方程,得x=30.
经检验,x=30是原方程的根,且符合题意,2x=60.
答:A工程队原来平均每天维修课桌60张.
(2)设C工程队提高工作效率后平均每天多维修课桌y张,施工2天后,已维修(60+60+30)×2=300(张), 从第3天起还需维修的张数应为600-300+360=660(张).
根据题意,得3(2y+2y+y+150)≤660≤4(2y+2y+y+150).
解这个不等式组,得3≤y≤14.
∴6≤2y≤28.
答:A工程队提高工作效率后平均每天多维修的课桌张数a的取值范围为6≤a≤28.
26.阅读下面材料,并解答问题.
材料:将分式拆分成一个整式与一个分式(分子为整数)的和的形式.
解:由分母为 x2+1,可设 x4 x2+3=( x2+1)(x2+a)+b
则 x4 x2+3=( x2+1)(x2+a)+b= x4 ax2+x2+a+b= x4 (a 1)x2+(a+b)
∵对应任意x,上述等式均成立,∴,∴a=2,b=1.
∴===
这样,分式被拆分成了一个整式与一个分式的和。
解答:
(1)请你仿照上述过程将分式拆分成一个整式与一个分式(分子为
整数)的和的形式.
(2)当时,试说明的最小值为8.
【知识点】分式的混合运算
【数学思想】整体思想
【思路点拨】只需仿照原材料中的解题过程就可解决问题.
【解答过程】解:(1)由分母为 x2+1,可设 x4 6x2+8=( x2+1)(x2+a)+b
则 x4 6x2+8=( x2+1)(x2+a)+b= x4 ax2+x2+a+b= x4 (a 1)x2+(a+b)
∵对应任意x,上述等式均成立,∴,∴a=7,b=1.
∴===
这样,分式被拆分成了一个整式与一个分式的和.
(2)当时,由=知,对于,
当x=0时,这两个式子的和有最小值,最小值为8,
即的最小值为8.
