人教版八年级数学上册《第十五章章末复习》名师课件(13张ppt)
文档属性
| 名称 | 人教版八年级数学上册《第十五章章末复习》名师课件(13张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-31 09:59:57 | ||
图片预览

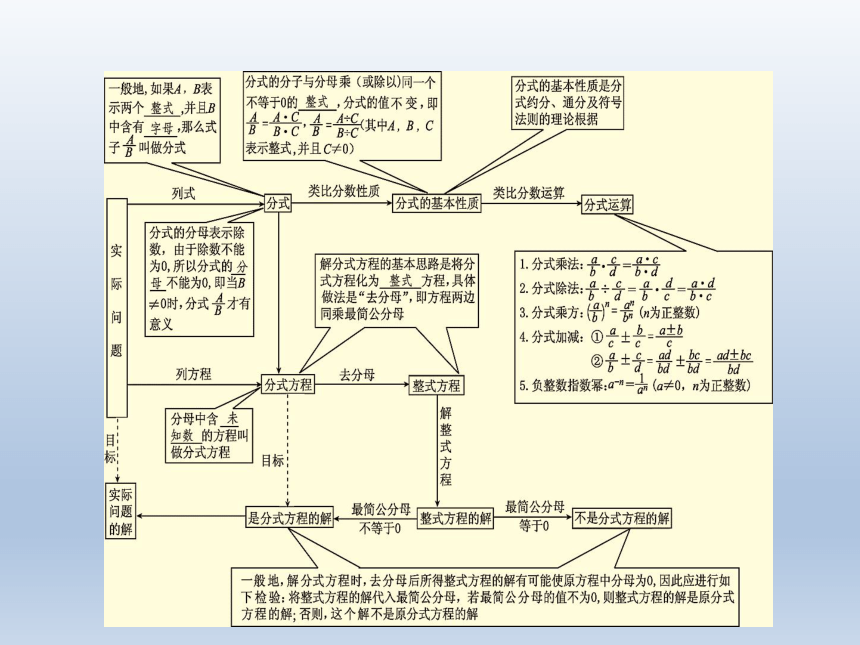




文档简介
(共13张PPT)
第十五章 章末复习
例1
下列各式中,哪些是整式? 哪些是分式?
, , , , , ,
解:整式有 ;
分式有 , .
, , , ,
【思路点拨】根据整式和分式的概念进行判断.在这里要认识到:(1) π表示圆周率,是一个无限不循环小数,即无理数;(2)单独的一个数是单项式,单项式是整式,所以 是整式;(3)给定一个式子不能化简后再去判断,要根据原来的形式进行判断,如 是分式,不能约分成a,误认为是整式.
计算:(1)
(2)
(3)
例2
【思路点拨】(1)因为b-a=-(a-b),而 ,所以通分时最简公分母为a-b,也可首先把前两项进行运算.
(2)把最后一个分式化简后再进行混合运算.
(3)可把y+2视作一个整体,首先进行括号内的运算,再进行括号外的运算.
计算:(1)
(2)
(3)
例2
解:(1)原式=
=
=
=
或者原式=
=1+1=2.
= 2
计算:(1)
(2)
(3)
例2
=
=
=
解:(2)原式=
=
计算:(1)
(2)
(3)
例2
=
=
=
=
解:(3)原式=
解下列分式方程:
例3
(1)
(2)
【思路点拨】
(1)方程中分母x2-1=(x+1)(x-1),所以方程两边同乘最简公分母(x+1)(x-1),注意不含分母的常数项1也要乘(x+1)(x-1);
(2)中方程的分母6x-2=2(3x-1),又因为1-3x=-(3x-1),所以方程两边同乘最简公分母2(3x-1),注意常数项 也要乘2(3x-1).
解下列分式方程:
例3
(1)
(2)
解:
(1)方程两边同乘(x+1)(x-1),得x(x+1)-2=(x+1)(x-1).
去括号,得x2+x-2=x2-1.
移项、合并同类项,得x=1.
检验:当x=1时,(x+1)(x-1)=0.
所以原分式方程无解.
解下列分式方程:
例3
(1)
(2)
解:
(2)原方程化为
方程两边同乘2(3x-1),得1=(3x-1)-4.
解得x=2.
检验:当x=2时,2(3x-1)≠0.
所以x=2是原分式方程的解.
甲、乙两车间生产同一种零件,乙车间比甲车间平均每小时多生产30个,甲车间生产600个零件与乙车间生产900个零件所用时间相等,设甲车间平均每小时生产x个零件,请按要求解决下列问题:
(1)根据题意,填写下表:
例4
车间 生产零件总个数 平均每小时生产零件的个数 所用时间
甲车间 600 x
乙车间 900 ________ ________
30+x
(2)甲、乙两车间平均每小时各生产多少个零件?
【思路点拨】先用x表示乙车间平均每小时生产的零件个数,再用x表示乙车间生产900个零件所用的时间,根据“时间相等”列方程.
解:(2)依题意列方程,得 ,
解得x=60,30+x=90.
当x=60时,x与30+x均不为0,且符合实际意义.
所以甲车间平均每小时生产60个零件,乙车间平均每小时生产90个零件.
选择“《分式》章末检测 ”
第十五章 章末复习
例1
下列各式中,哪些是整式? 哪些是分式?
, , , , , ,
解:整式有 ;
分式有 , .
, , , ,
【思路点拨】根据整式和分式的概念进行判断.在这里要认识到:(1) π表示圆周率,是一个无限不循环小数,即无理数;(2)单独的一个数是单项式,单项式是整式,所以 是整式;(3)给定一个式子不能化简后再去判断,要根据原来的形式进行判断,如 是分式,不能约分成a,误认为是整式.
计算:(1)
(2)
(3)
例2
【思路点拨】(1)因为b-a=-(a-b),而 ,所以通分时最简公分母为a-b,也可首先把前两项进行运算.
(2)把最后一个分式化简后再进行混合运算.
(3)可把y+2视作一个整体,首先进行括号内的运算,再进行括号外的运算.
计算:(1)
(2)
(3)
例2
解:(1)原式=
=
=
=
或者原式=
=1+1=2.
= 2
计算:(1)
(2)
(3)
例2
=
=
=
解:(2)原式=
=
计算:(1)
(2)
(3)
例2
=
=
=
=
解:(3)原式=
解下列分式方程:
例3
(1)
(2)
【思路点拨】
(1)方程中分母x2-1=(x+1)(x-1),所以方程两边同乘最简公分母(x+1)(x-1),注意不含分母的常数项1也要乘(x+1)(x-1);
(2)中方程的分母6x-2=2(3x-1),又因为1-3x=-(3x-1),所以方程两边同乘最简公分母2(3x-1),注意常数项 也要乘2(3x-1).
解下列分式方程:
例3
(1)
(2)
解:
(1)方程两边同乘(x+1)(x-1),得x(x+1)-2=(x+1)(x-1).
去括号,得x2+x-2=x2-1.
移项、合并同类项,得x=1.
检验:当x=1时,(x+1)(x-1)=0.
所以原分式方程无解.
解下列分式方程:
例3
(1)
(2)
解:
(2)原方程化为
方程两边同乘2(3x-1),得1=(3x-1)-4.
解得x=2.
检验:当x=2时,2(3x-1)≠0.
所以x=2是原分式方程的解.
甲、乙两车间生产同一种零件,乙车间比甲车间平均每小时多生产30个,甲车间生产600个零件与乙车间生产900个零件所用时间相等,设甲车间平均每小时生产x个零件,请按要求解决下列问题:
(1)根据题意,填写下表:
例4
车间 生产零件总个数 平均每小时生产零件的个数 所用时间
甲车间 600 x
乙车间 900 ________ ________
30+x
(2)甲、乙两车间平均每小时各生产多少个零件?
【思路点拨】先用x表示乙车间平均每小时生产的零件个数,再用x表示乙车间生产900个零件所用的时间,根据“时间相等”列方程.
解:(2)依题意列方程,得 ,
解得x=60,30+x=90.
当x=60时,x与30+x均不为0,且符合实际意义.
所以甲车间平均每小时生产60个零件,乙车间平均每小时生产90个零件.
选择“《分式》章末检测 ”
