人教版 六年级上册数学 数学广角—数与形解答题综合训练 (含答案)
文档属性
| 名称 | 人教版 六年级上册数学 数学广角—数与形解答题综合训练 (含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 459.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-30 16:40:11 | ||
图片预览

文档简介
人教版六年级上册数学数学广角—数与形解答题综合训练
1.一张桌子坐6人,两张桌子并起来坐10人,三张桌子并起来坐14人,……,照这样8张桌子可以坐几人?如果有58人,需要并多少张桌子?
2.一个长方形把平面分成两部分,那么3个长方形最多把平面分成多少部分?
3.一张桌子坐4人,两张桌子并起来坐6人,三张桌子并起来坐8人,如图所示,照这样,9张桌子并成一排可以坐多少人?如果一共有30人,需要并多少张桌子才能坐下?
4.四年下面火柴棒摆的算式都是错的,请在各式中去掉或添加1根火柴棒,使各式成立。
(1)
(2)
(3)
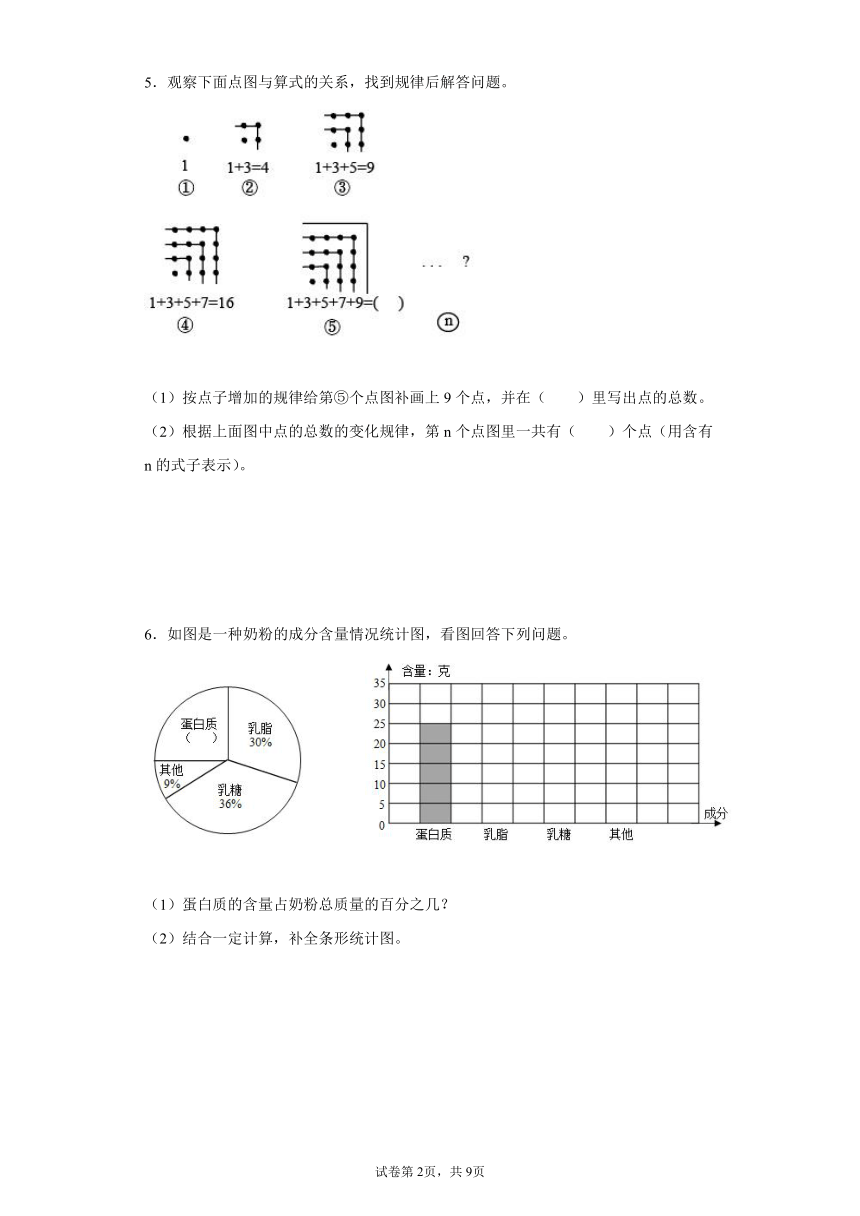
5.观察下面点图与算式的关系,找到规律后解答问题。
(1)按点子增加的规律给第⑤个点图补画上9个点,并在( )里写出点的总数。
(2)根据上面图中点的总数的变化规律,第n个点图里一共有( )个点(用含有n的式子表示)。
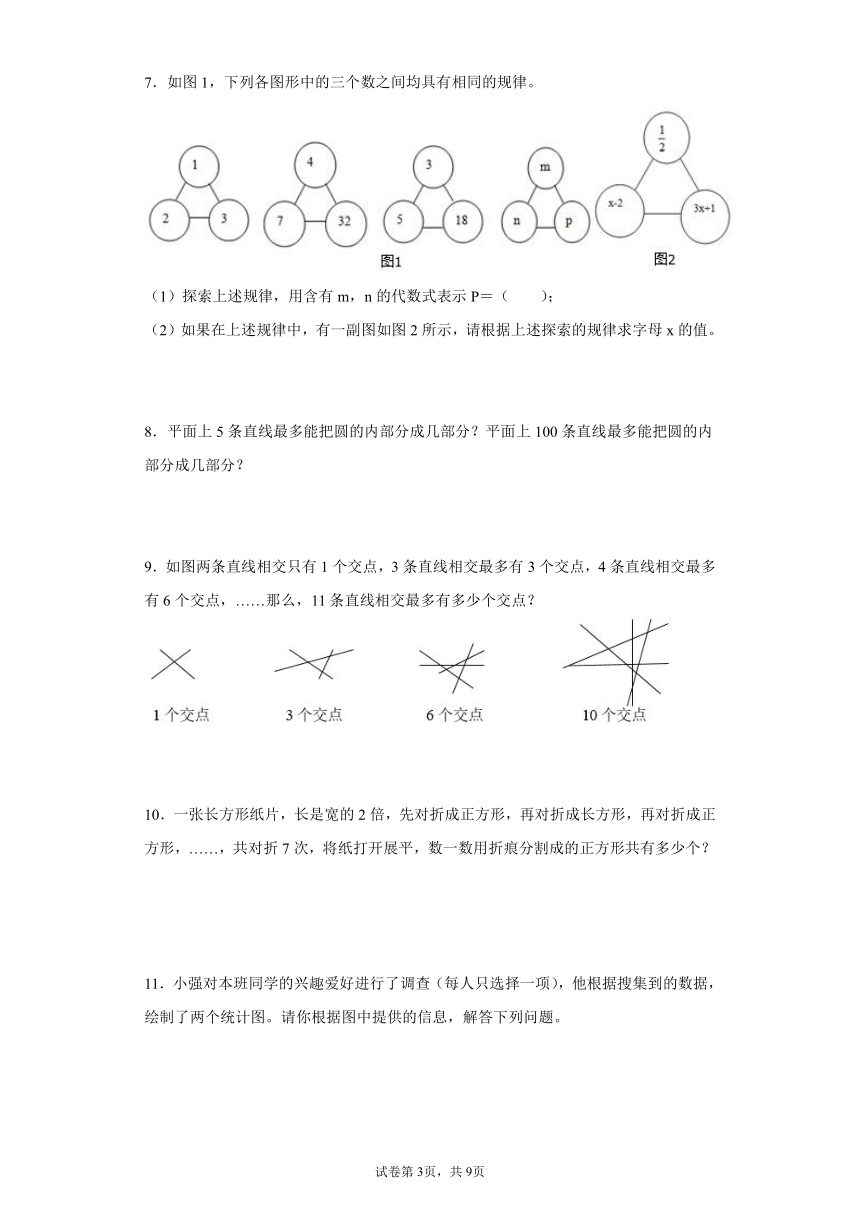
6.如图是一种奶粉的成分含量情况统计图,看图回答下列问题。
(1)蛋白质的含量占奶粉总质量的百分之几?
(2)结合一定计算,补全条形统计图。
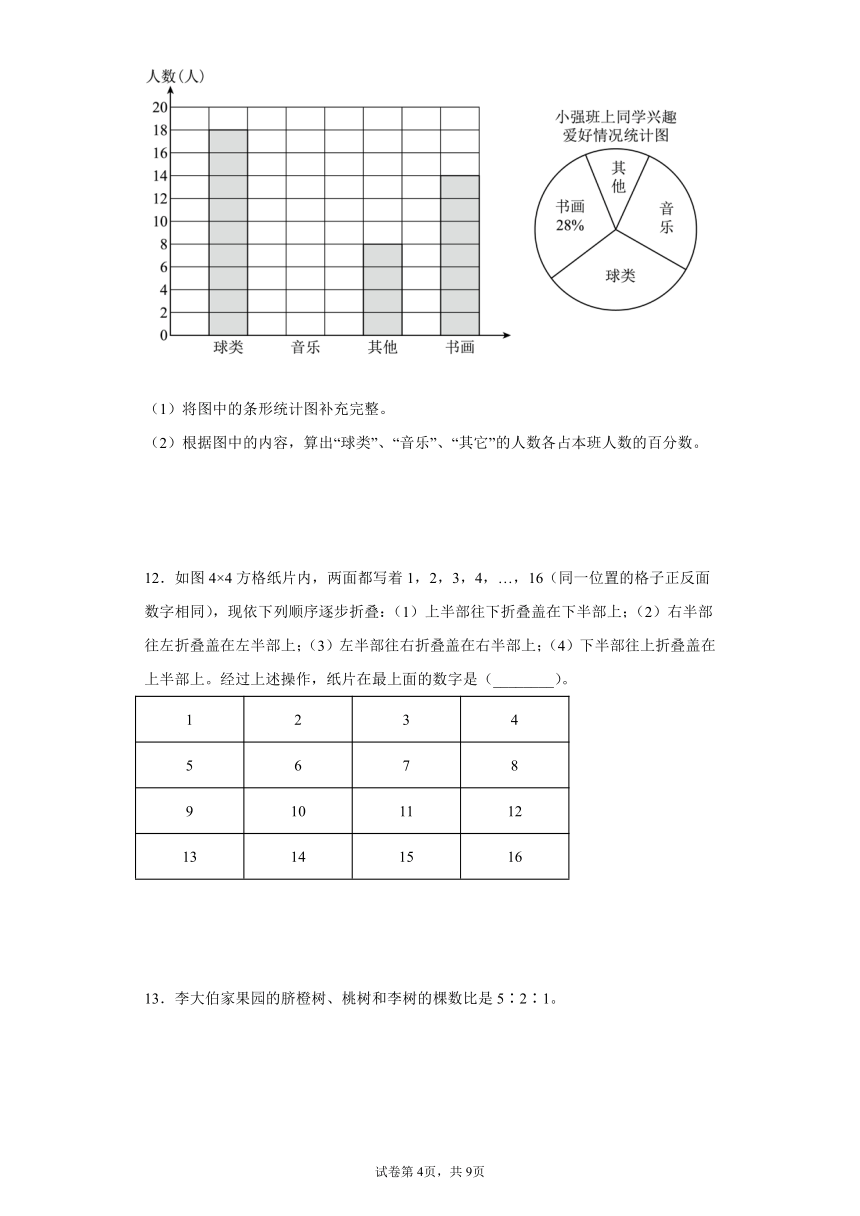
7.如图1,下列各图形中的三个数之间均具有相同的规律。
(1)探索上述规律,用含有m,n的代数式表示P=( );
(2)如果在上述规律中,有一副图如图2所示,请根据上述探索的规律求字母x的值。
8.平面上5条直线最多能把圆的内部分成几部分?平面上100条直线最多能把圆的内部分成几部分?
9.如图两条直线相交只有1个交点,3条直线相交最多有3个交点,4条直线相交最多有6个交点,……那么,11条直线相交最多有多少个交点?
10.一张长方形纸片,长是宽的2倍,先对折成正方形,再对折成长方形,再对折成正方形,……,共对折7次,将纸打开展平,数一数用折痕分割成的正方形共有多少个?
11.小强对本班同学的兴趣爱好进行了调查(每人只选择一项),他根据搜集到的数据,绘制了两个统计图。请你根据图中提供的信息,解答下列问题。
(1)将图中的条形统计图补充完整。
(2)根据图中的内容,算出“球类”、“音乐”、“其它”的人数各占本班人数的百分数。
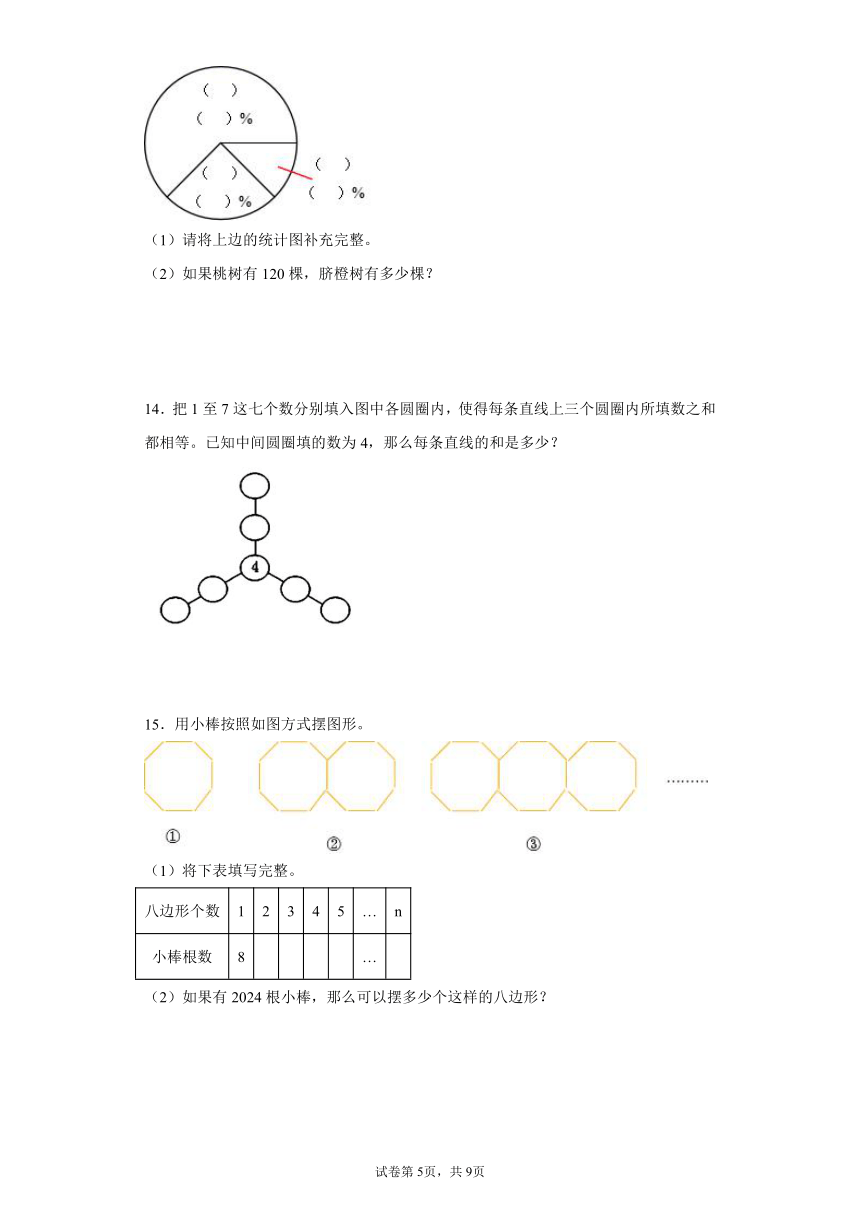
12.如图4×4方格纸片内,两面都写着1,2,3,4,…,16(同一位置的格子正反面数字相同),现依下列顺序逐步折叠:(1)上半部往下折叠盖在下半部上;(2)右半部往左折叠盖在左半部上;(3)左半部往右折叠盖在右半部上;(4)下半部往上折叠盖在上半部上。经过上述操作,纸片在最上面的数字是(________)。
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 16
13.李大伯家果园的脐橙树、桃树和李树的棵数比是5∶2∶1。
(1)请将上边的统计图补充完整。
(2)如果桃树有120棵,脐橙树有多少棵?
14.把1至7这七个数分别填入图中各圆圈内,使得每条直线上三个圆圈内所填数之和都相等。已知中间圆圈填的数为4,那么每条直线的和是多少?
15.用小棒按照如图方式摆图形。
(1)将下表填写完整。
八边形个数 1 2 3 4 5 … n
小棒根数 8 …
(2)如果有2024根小棒,那么可以摆多少个这样的八边形?
16.下图是六年级同学参加课外兴趣小组情况统计情况,已知六年级有120人,三个兴趣小组分别有多少人?
17.在一大块面包上切刀最多能将面包切成多少块。(注:面包是一个立体几何图形,切面可以是任何方向)
18.请将1、2、3、4、5、6、7、8八个数字填入右图中的八块区域内,使得每一个圆圈与它相邻的区域内的数之和都相等。
19.数形结合是一种重要的数学思想。请你画出第五个图形并思考:第10个方框有多少个点?第51个方框有多少个点?
1 1+4 1+4×2 1+4×3 ( )
20.在图中的A、B、C三个圆圈内填入三个不同的自然数,使得三角形每条边上的三个数之和都等于12,那么圆圈B中应填的数是多少?
21.为庆祝“六一”儿童节,某幼儿园举行用火柴棒摆“金鱼”比赛。如图所示,按照下面的规律摆下去。
(1)摆6个“金鱼”需要多少根火柴棒?
(2)摆n个“金鱼”需要多少根火柴棒?
(3)若有2018根火柴棒,那么可以摆多少个“金鱼”?
22.下图是丽丽家十月份生活支出统计图。
(1)这是( )统计图。从图中可以看出哪项支出最多?
(2)如果丽丽家十月份的食品支出是720元,十月份总支出是多少元?
(3)根据统计图,请你再提一个数学问题并解答。
23.有一组图形按下面规律排列。
(1)第10个图形中白色小正方形和黑色小正方形各有多少个?
(2)如果某个图形中有38个白色小正方形,那么这个图形排在第几?
24.观察下列等式:
第1个等式:;
第2个等式:;
第3个等式:;
第4个等式:;
……
请解答下列问题:
(1)按以上规律列出第5个等式:=( )=( );
(2)求的值。
25.下图的两个图形(实线)是分别用10根和16根单位长的小棍围成的。如果按此规律(每一层比上面一层多摆出两个小正方形)围成的图形共用了60多根小棍,那么围成的图形有几层,共用了多少根小棍?
26.用同样长的小棒摆正方形,如图:
(1)填一填。(每空1分,共2分)
正方形个数 1 2 3 4 5 …
小棒根数 1+3×1 1+3×2 1+3×3 …
(2)这样摆7个正方形,需要多少根小棒?
(3)现有31根小棒,能摆多少个这样的正方形?
27.一条直线分一个平面为两部分。两条直线最多分这个平面为四部分。问5条直线最多分这个平面为多少部分?
28.观察算式的规律:,,,,……。用含字母的式子表示规律:(________)。
用规律计算:(________)。
29.有一座四层楼房,每个窗户的4块玻璃分别涂上红色和白色,每个窗户代表一个数字,每层楼有三个窗户,由左向右表示一个三位数,四个楼层表示的三位数有:791、275、362、612。问:第二层楼表示哪个三位数?
参考答案
1.34人;14张
2.26部分
3.20人;14张
4.(1)或者
(2)
(3)去掉一根将53变成52即可
5.(1)25;
(2)n2
6.(1)25%;
(2)见详解
7.(1)(n+1)×m;
(2)﹣0.6
8.16部分;5051部分
9.55个
10.个
11.(1)见详解;
(2)“球类”、“音乐”、“其它”的人数各占本班人数的百分数分别为36%、20%、16%。
12.14
13.(1)见详解;
(2)300棵
14.12
15.(1) 15; 22;29;36;;
(2)289个
16.美术:12人;文艺:36人;体育:72人
17.块
18.
19.第五个图形见解析;37个;201个;1+4×4
20.5
21.(1)38根;(2)2+6n;(3)336个
22.(1)扇形;食品支出;
(2)2000元;
(3)水电气支出比文化支出少百分之几?50%
23.(1)白:26个;黑:10个
(2)16
24.(1);;(2)
25.层,根
26.(1)见详解
(2)22根
(3)10个
27.16部分
28.n2 (n 1)2=n+n+1 210
29.612
试卷第8页,共9页
试卷第9页,共9页
1.一张桌子坐6人,两张桌子并起来坐10人,三张桌子并起来坐14人,……,照这样8张桌子可以坐几人?如果有58人,需要并多少张桌子?
2.一个长方形把平面分成两部分,那么3个长方形最多把平面分成多少部分?
3.一张桌子坐4人,两张桌子并起来坐6人,三张桌子并起来坐8人,如图所示,照这样,9张桌子并成一排可以坐多少人?如果一共有30人,需要并多少张桌子才能坐下?
4.四年下面火柴棒摆的算式都是错的,请在各式中去掉或添加1根火柴棒,使各式成立。
(1)
(2)
(3)
5.观察下面点图与算式的关系,找到规律后解答问题。
(1)按点子增加的规律给第⑤个点图补画上9个点,并在( )里写出点的总数。
(2)根据上面图中点的总数的变化规律,第n个点图里一共有( )个点(用含有n的式子表示)。
6.如图是一种奶粉的成分含量情况统计图,看图回答下列问题。
(1)蛋白质的含量占奶粉总质量的百分之几?
(2)结合一定计算,补全条形统计图。
7.如图1,下列各图形中的三个数之间均具有相同的规律。
(1)探索上述规律,用含有m,n的代数式表示P=( );
(2)如果在上述规律中,有一副图如图2所示,请根据上述探索的规律求字母x的值。
8.平面上5条直线最多能把圆的内部分成几部分?平面上100条直线最多能把圆的内部分成几部分?
9.如图两条直线相交只有1个交点,3条直线相交最多有3个交点,4条直线相交最多有6个交点,……那么,11条直线相交最多有多少个交点?
10.一张长方形纸片,长是宽的2倍,先对折成正方形,再对折成长方形,再对折成正方形,……,共对折7次,将纸打开展平,数一数用折痕分割成的正方形共有多少个?
11.小强对本班同学的兴趣爱好进行了调查(每人只选择一项),他根据搜集到的数据,绘制了两个统计图。请你根据图中提供的信息,解答下列问题。
(1)将图中的条形统计图补充完整。
(2)根据图中的内容,算出“球类”、“音乐”、“其它”的人数各占本班人数的百分数。
12.如图4×4方格纸片内,两面都写着1,2,3,4,…,16(同一位置的格子正反面数字相同),现依下列顺序逐步折叠:(1)上半部往下折叠盖在下半部上;(2)右半部往左折叠盖在左半部上;(3)左半部往右折叠盖在右半部上;(4)下半部往上折叠盖在上半部上。经过上述操作,纸片在最上面的数字是(________)。
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 16
13.李大伯家果园的脐橙树、桃树和李树的棵数比是5∶2∶1。
(1)请将上边的统计图补充完整。
(2)如果桃树有120棵,脐橙树有多少棵?
14.把1至7这七个数分别填入图中各圆圈内,使得每条直线上三个圆圈内所填数之和都相等。已知中间圆圈填的数为4,那么每条直线的和是多少?
15.用小棒按照如图方式摆图形。
(1)将下表填写完整。
八边形个数 1 2 3 4 5 … n
小棒根数 8 …
(2)如果有2024根小棒,那么可以摆多少个这样的八边形?
16.下图是六年级同学参加课外兴趣小组情况统计情况,已知六年级有120人,三个兴趣小组分别有多少人?
17.在一大块面包上切刀最多能将面包切成多少块。(注:面包是一个立体几何图形,切面可以是任何方向)
18.请将1、2、3、4、5、6、7、8八个数字填入右图中的八块区域内,使得每一个圆圈与它相邻的区域内的数之和都相等。
19.数形结合是一种重要的数学思想。请你画出第五个图形并思考:第10个方框有多少个点?第51个方框有多少个点?
1 1+4 1+4×2 1+4×3 ( )
20.在图中的A、B、C三个圆圈内填入三个不同的自然数,使得三角形每条边上的三个数之和都等于12,那么圆圈B中应填的数是多少?
21.为庆祝“六一”儿童节,某幼儿园举行用火柴棒摆“金鱼”比赛。如图所示,按照下面的规律摆下去。
(1)摆6个“金鱼”需要多少根火柴棒?
(2)摆n个“金鱼”需要多少根火柴棒?
(3)若有2018根火柴棒,那么可以摆多少个“金鱼”?
22.下图是丽丽家十月份生活支出统计图。
(1)这是( )统计图。从图中可以看出哪项支出最多?
(2)如果丽丽家十月份的食品支出是720元,十月份总支出是多少元?
(3)根据统计图,请你再提一个数学问题并解答。
23.有一组图形按下面规律排列。
(1)第10个图形中白色小正方形和黑色小正方形各有多少个?
(2)如果某个图形中有38个白色小正方形,那么这个图形排在第几?
24.观察下列等式:
第1个等式:;
第2个等式:;
第3个等式:;
第4个等式:;
……
请解答下列问题:
(1)按以上规律列出第5个等式:=( )=( );
(2)求的值。
25.下图的两个图形(实线)是分别用10根和16根单位长的小棍围成的。如果按此规律(每一层比上面一层多摆出两个小正方形)围成的图形共用了60多根小棍,那么围成的图形有几层,共用了多少根小棍?
26.用同样长的小棒摆正方形,如图:
(1)填一填。(每空1分,共2分)
正方形个数 1 2 3 4 5 …
小棒根数 1+3×1 1+3×2 1+3×3 …
(2)这样摆7个正方形,需要多少根小棒?
(3)现有31根小棒,能摆多少个这样的正方形?
27.一条直线分一个平面为两部分。两条直线最多分这个平面为四部分。问5条直线最多分这个平面为多少部分?
28.观察算式的规律:,,,,……。用含字母的式子表示规律:(________)。
用规律计算:(________)。
29.有一座四层楼房,每个窗户的4块玻璃分别涂上红色和白色,每个窗户代表一个数字,每层楼有三个窗户,由左向右表示一个三位数,四个楼层表示的三位数有:791、275、362、612。问:第二层楼表示哪个三位数?
参考答案
1.34人;14张
2.26部分
3.20人;14张
4.(1)或者
(2)
(3)去掉一根将53变成52即可
5.(1)25;
(2)n2
6.(1)25%;
(2)见详解
7.(1)(n+1)×m;
(2)﹣0.6
8.16部分;5051部分
9.55个
10.个
11.(1)见详解;
(2)“球类”、“音乐”、“其它”的人数各占本班人数的百分数分别为36%、20%、16%。
12.14
13.(1)见详解;
(2)300棵
14.12
15.(1) 15; 22;29;36;;
(2)289个
16.美术:12人;文艺:36人;体育:72人
17.块
18.
19.第五个图形见解析;37个;201个;1+4×4
20.5
21.(1)38根;(2)2+6n;(3)336个
22.(1)扇形;食品支出;
(2)2000元;
(3)水电气支出比文化支出少百分之几?50%
23.(1)白:26个;黑:10个
(2)16
24.(1);;(2)
25.层,根
26.(1)见详解
(2)22根
(3)10个
27.16部分
28.n2 (n 1)2=n+n+1 210
29.612
试卷第8页,共9页
试卷第9页,共9页
