2021—2022学年人教版九年级数学上册24.2 点和圆、直线与圆的位置关系 同步练习题(Word版含答案)
文档属性
| 名称 | 2021—2022学年人教版九年级数学上册24.2 点和圆、直线与圆的位置关系 同步练习题(Word版含答案) | 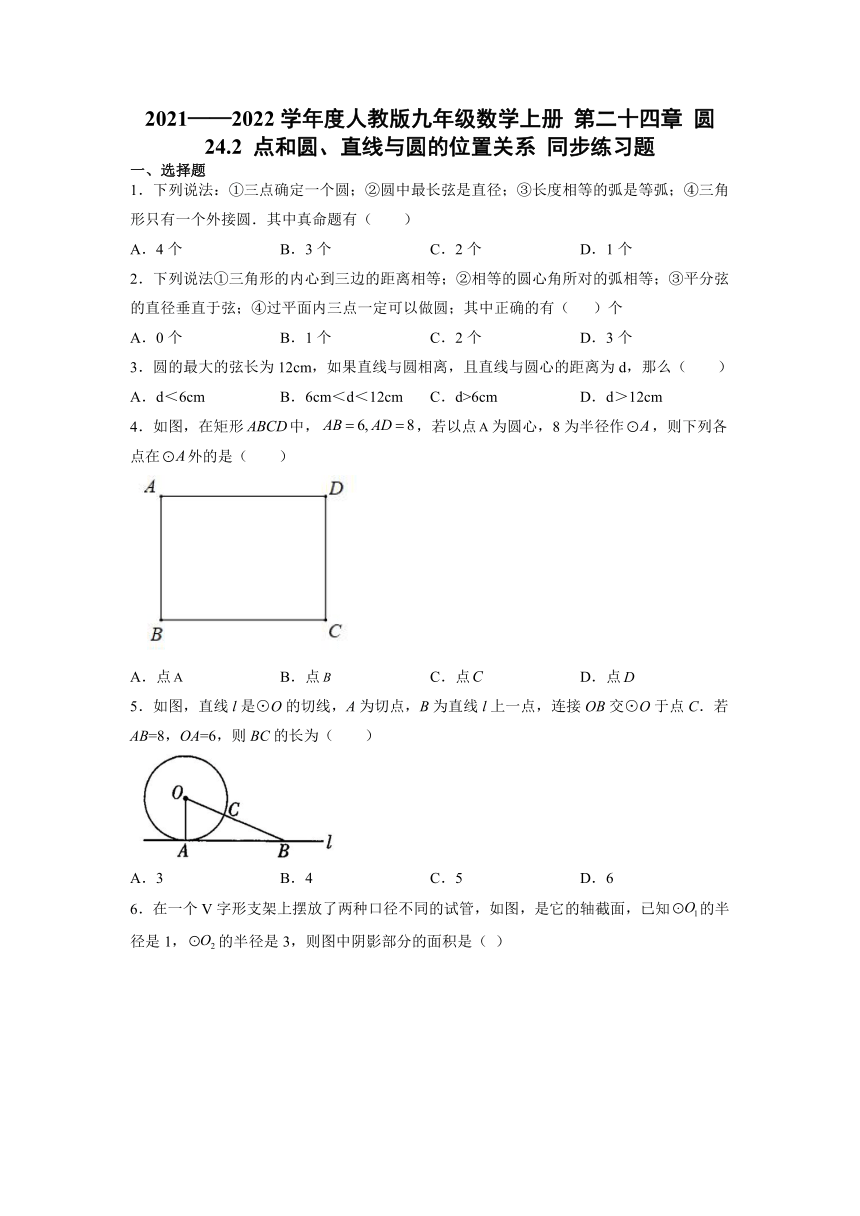 | |
| 格式 | docx | ||
| 文件大小 | 414.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-30 22:56:29 | ||
图片预览


文档简介
2021——2022学年度人教版九年级数学上册 第二十四章 圆
24.2 点和圆、直线与圆的位置关系 同步练习题
一、选择题
1.下列说法:①三点确定一个圆;②圆中最长弦是直径;③长度相等的弧是等弧;④三角形只有一个外接圆.其中真命题有( )
A.4个 B.3个 C.2个 D.1个
2.下列说法①三角形的内心到三边的距离相等;②相等的圆心角所对的弧相等;③平分弦的直径垂直于弦;④过平面内三点一定可以做圆;其中正确的有( )个
A.0个 B.1个 C.2个 D.3个
3.圆的最大的弦长为12cm,如果直线与圆相离,且直线与圆心的距离为d,那么( )
A.d<6cm B.6cm<d<12cm C.d>6cm D.d>12cm
4.如图,在矩形中,,若以点为圆心,8为半径作,则下列各点在外的是( )
A.点 B.点 C.点 D.点
5.如图,直线l是⊙O的切线,A为切点,B为直线l上一点,连接OB交⊙O于点C.若AB=8,OA=6,则BC的长为( )
A.3 B.4 C.5 D.6
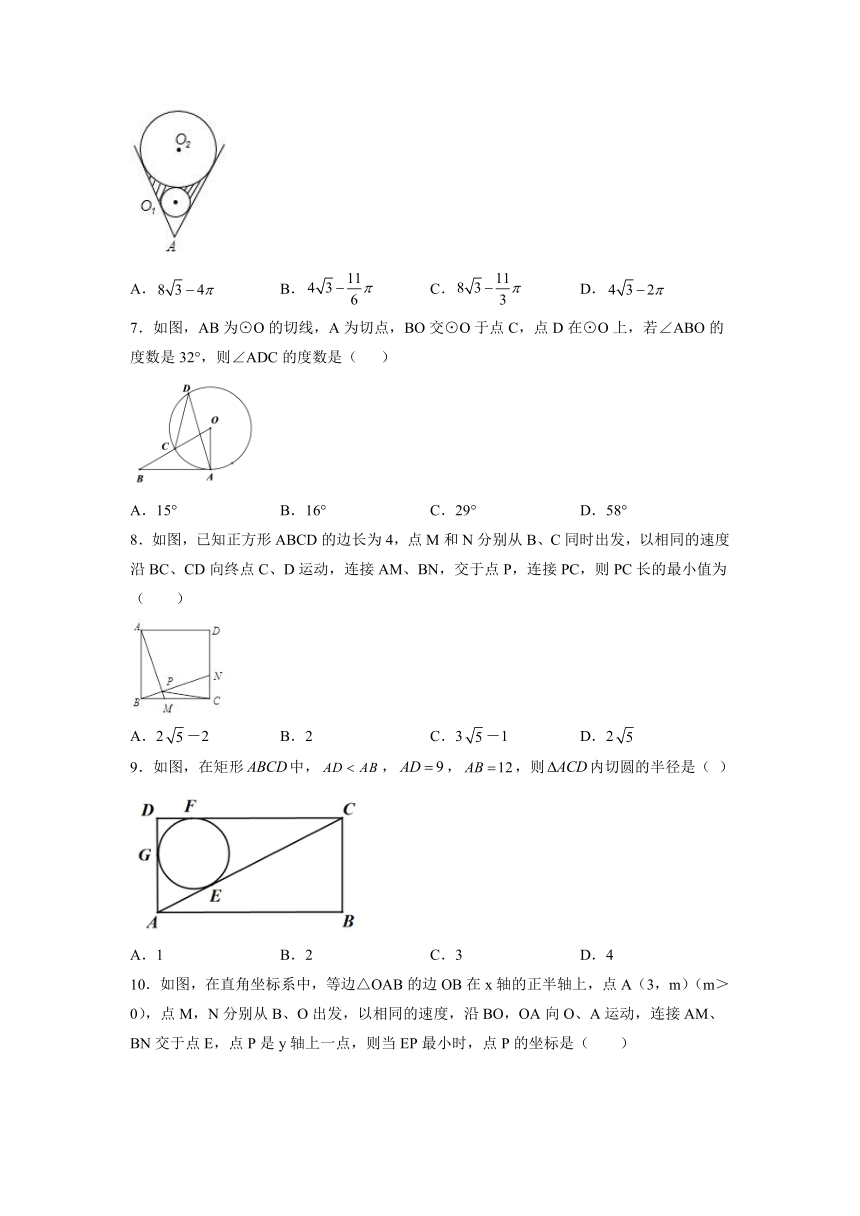
6.在一个V字形支架上摆放了两种口径不同的试管,如图,是它的轴截面,已知的半径是1,的半径是3,则图中阴影部分的面积是( )
A. B. C. D.
7.如图,AB为⊙O的切线,A为切点,BO交⊙O于点C,点D在⊙O上,若∠ABO的度数是32°,则∠ADC的度数是( )
A.15° B.16° C.29° D.58°
8.如图,已知正方形ABCD的边长为4,点M和N分别从B、C同时出发,以相同的速度沿BC、CD向终点C、D运动,连接AM、BN,交于点P,连接PC,则PC长的最小值为( )
A.2-2 B.2 C.3-1 D.2
9.如图,在矩形中,,,,则内切圆的半径是( )
A.1 B.2 C.3 D.4
10.如图,在直角坐标系中,等边△OAB的边OB在x轴的正半轴上,点A(3,m)(m>0),点M,N分别从B、O出发,以相同的速度,沿BO,OA向O、A运动,连接AM、BN交于点E,点P是y轴上一点,则当EP最小时,点P的坐标是( )
A.(0,) B.(0,2) C.(0,3) D.(0,)
二、填空题
11.中,,,,则的外接圆半径长是________.
12.为半圆O的直径,C为半圆弧的一个三等分点,过B,C两点的半圆O的切线交于点P,则________.
13.中,,,点是的外心,则的长为______.
14.如图,PA、PB是⊙O的切线,切点分别为A、B,若OA=2,∠P=60°,则AB的长为________
15.如图,AB是⊙O的直径,AC是⊙O的切线,连接OC交⊙O于点D,连接BD,∠B=25 ,则∠C的度数是_______.
三、解答题
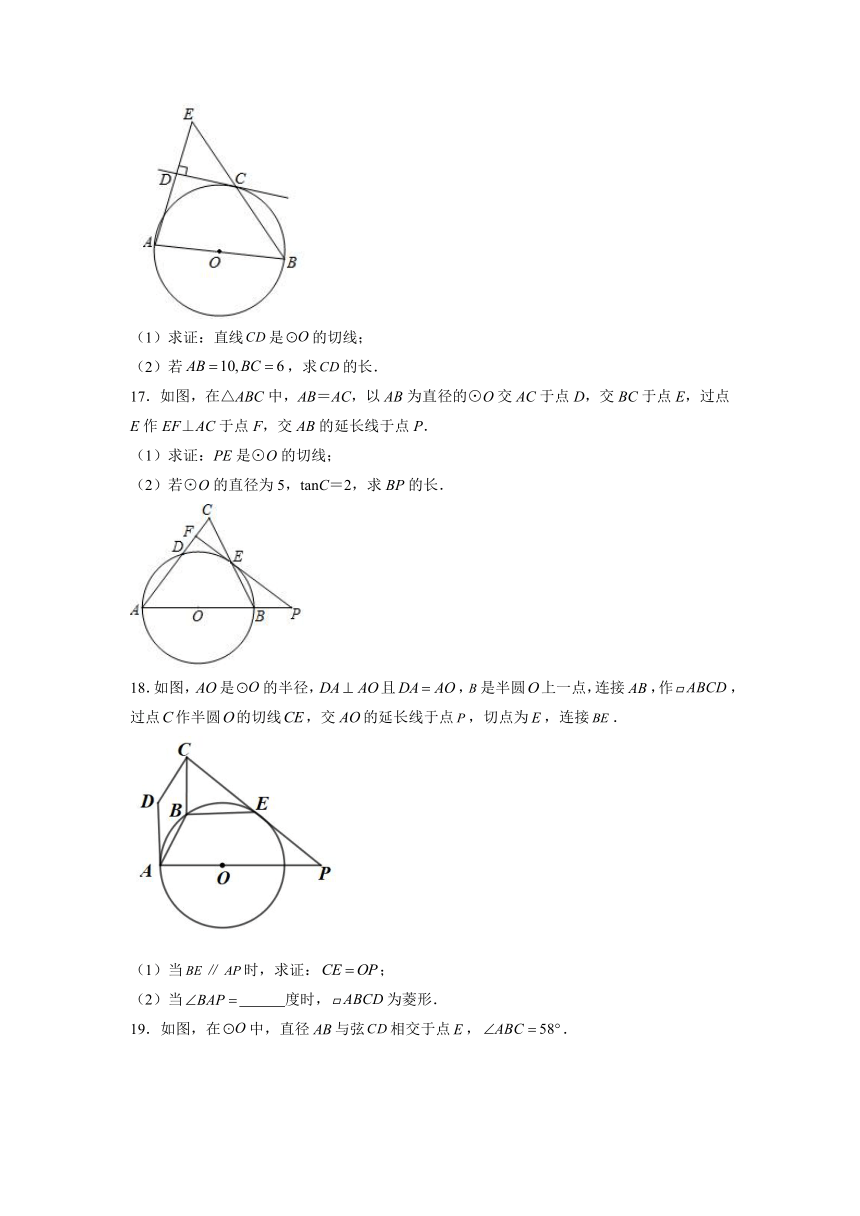
16.如图,为的直径,,交于点C,于D.
(1)求证:直线是的切线;
(2)若,求的长.
17.如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC于点D,交BC于点E,过点E作EF⊥AC于点F,交AB的延长线于点P.
(1)求证:PE是⊙O的切线;
(2)若⊙O的直径为5,tanC=2,求BP的长.
18.如图,是的半径,且,是半圆上一点,连接,作,过点作半圆的切线,交的延长线于点,切点为,连接.
(1)当∥时,求证:;
(2)当 度时,为菱形.
19.如图,在中,直径与弦相交于点,.
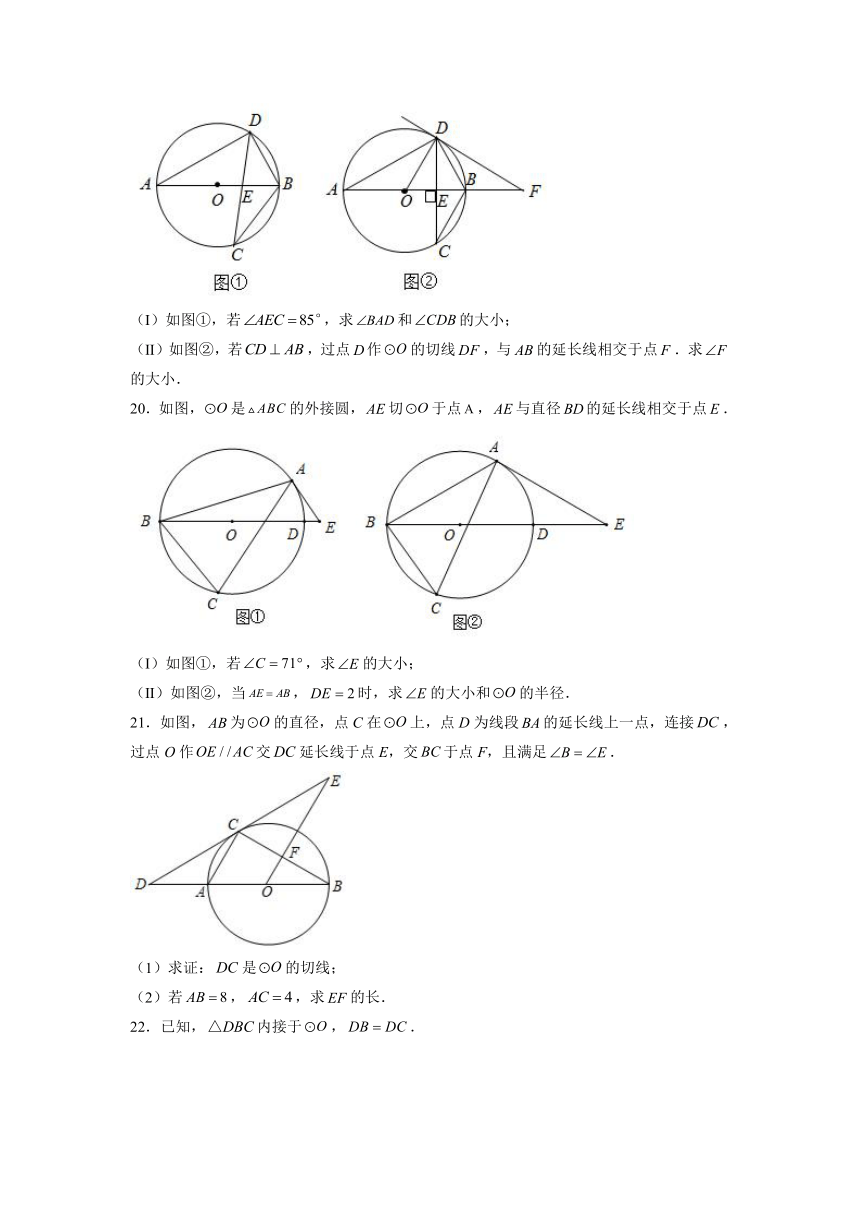
(Ⅰ)如图①,若,求和的大小;
(Ⅱ)如图②,若,过点作的切线,与的延长线相交于点.求的大小.
20.如图,是的外接圆,切于点,与直径的延长线相交于点.
(Ⅰ)如图①,若,求的大小;
(Ⅱ)如图②,当,时,求的大小和的半径.
21.如图,为的直径,点C在上,点D为线段的延长线上一点,连接,过点O作交延长线于点E,交于点F,且满足.
(1)求证:是的切线;
(2)若,,求的长.
22.已知,内接于,.
(1)如图①,过点作射线交于点,若,求的度数.
(2)如图②,分别过点、点作的切线相交于点,若,求的度数.
23.我们将能完全覆盖某平面图形的最小圆称为该平面图形的最小覆盖圆.例如线段的最小覆盖圆就是以线段为直径的圆.锐角三角形的最小覆盖圆是该三角形的外接圆.
(1)分别在图1,图2中作出的最小覆盖圆.(要求尺规作图,保留作图痕迹,不写作法);
(2)根据(1)中的作图,钝角三角形的最小覆盖圆是______;
某地要修建一个基站,服务四个村庄E、F、G、H(其位置如图3所示),为使信号可以覆盖四个村庄,且基站所需发射功率最小(距离越小,所需功率越小),此基站应建在何处?请说明理由.
【参考答案】
1.C 2.B 3.C 4.C 5.B 6.C 7.C 8.A 9.C 10.B
11.
12.或
13.
14.
15.40°
16.解:(1)证明:连接,如图,
∵,
∴,
∵,
∴,
∴;
∵,
∴,
∴,
∴,
∴,
又∴是的半径,
∴直线是的切线.
(2)解:连接,
∵为直径,
∴,
∴,
∵,
∴,
∵,
∴.
17.解:(1)证明:连接,,
,
,
,
,
,
,
,
,
是的切线;
(2)为的直径,
,AB=AC=5,
,
,
设,,
,
,
(负值舍去),
,,
,
,
,
,
,
,
,
,
,
,
,
.
18.(1)证明:延长CB交AP于点F,连接OB、OE,
∵AD⊥AO,AD∥BC,
∴CF⊥AP,
∵BE∥AP,CF⊥AP,
∴CB⊥BE,即∠CBE=90°,
∵CE是⊙O的切线,则∠OEP=90°=∠CBE,
∵四边形ABCD是平行四边形,
∴AD=BC=AO=OE,
∵BE∥AP,
∴∠P=∠CEB,
在△CBE和△OEP中,
,
∴△CBE≌△OEP(AAS),
∴CE=OP;
(2)解:∵ ABCD为菱形,
∴DA=AB=AO=OB,
∴△BAO为等边三角形,
∴∠BAP等于60度时, ABCD为菱形,
故答案为:60.
19.解:(Ⅰ)∵,
∴∠C=
∴
∵直径与弦相交于点,
∴∠ADB=90°,
又∵
∴
(Ⅱ)∵
∴∠AEC=90°
又∵
∴
∴
∵是的切线
∴
∴
20.解:(Ⅰ)连接.
∵切于点,
∴,∴,
∵,
∴,
∴.
(Ⅱ)连接,设.
∵,∴,
∵,∴,
∴.
∵是的切线,
∴,即,
在中,,
即,
解得,
∴.
在中,,
∵,
∴,
∵,
∴,即的半径为2.
21.解:(1)连接OC,如图所示:
∵AB为⊙O的直径,
∴∠ACB=∠ACO+∠OCB=90°,
∵OB,OC是⊙O的半径,
∴OB=OC,
∴∠B=∠OCB,
∴∠ACO+∠B=90°,
∵OE∥AC,
∴∠ACD=∠E,
∵∠B=∠E,
∴∠ACD=∠B,
∴∠ACO+∠ACD=90°,即∠OCD=90°,即OC⊥CD,
∴CD是圆O的切线;
(2)∵AB=8,AC=4,
∴OC=AC=4,
又∵∠ACB=∠OCE=90°,∠B=∠E,
∴△ACB≌△OCE(AAS),
∴AB=OE=8,
∵OE∥AC,点O为AB中点,
∴OF=AC=2,
∴EF=OE-OF=6.
22.(1)解:∵四边形是的内接四边形,
∴,
∵,
∴,
∵,
∴,
∵,
∴,
∴;
(2)解:连结、,
∵、与相切于点、,
∴,,
∴,,
∵,,
∴,
∴,
∵,
∴,
∴;
23.(1)作图如下图所示;
(2)以最长边为直径的圆;
理由:∵线段的最小覆盖圆就是以线段为直径的圆,
由于∠A为钝角,因此∠A在圆内,
∴该圆为能完全覆盖该钝角三角形的最小圆.
(3)的外心(外接圆的圆心)
理由:如图,的外接圆刚好覆盖E,F,H三点,与直线交于点D,连接DH和DF
∵,
且,
∴,
∵∠HGF=50°+60°=110°,
∴.
∴点G在点E,D之间.
即点G被外接圆覆盖,
此时该圆为能完全覆盖该四边形的最小圆.
因此,此基站应建在的外心处.
24.2 点和圆、直线与圆的位置关系 同步练习题
一、选择题
1.下列说法:①三点确定一个圆;②圆中最长弦是直径;③长度相等的弧是等弧;④三角形只有一个外接圆.其中真命题有( )
A.4个 B.3个 C.2个 D.1个
2.下列说法①三角形的内心到三边的距离相等;②相等的圆心角所对的弧相等;③平分弦的直径垂直于弦;④过平面内三点一定可以做圆;其中正确的有( )个
A.0个 B.1个 C.2个 D.3个
3.圆的最大的弦长为12cm,如果直线与圆相离,且直线与圆心的距离为d,那么( )
A.d<6cm B.6cm<d<12cm C.d>6cm D.d>12cm
4.如图,在矩形中,,若以点为圆心,8为半径作,则下列各点在外的是( )
A.点 B.点 C.点 D.点
5.如图,直线l是⊙O的切线,A为切点,B为直线l上一点,连接OB交⊙O于点C.若AB=8,OA=6,则BC的长为( )
A.3 B.4 C.5 D.6
6.在一个V字形支架上摆放了两种口径不同的试管,如图,是它的轴截面,已知的半径是1,的半径是3,则图中阴影部分的面积是( )
A. B. C. D.
7.如图,AB为⊙O的切线,A为切点,BO交⊙O于点C,点D在⊙O上,若∠ABO的度数是32°,则∠ADC的度数是( )
A.15° B.16° C.29° D.58°
8.如图,已知正方形ABCD的边长为4,点M和N分别从B、C同时出发,以相同的速度沿BC、CD向终点C、D运动,连接AM、BN,交于点P,连接PC,则PC长的最小值为( )
A.2-2 B.2 C.3-1 D.2
9.如图,在矩形中,,,,则内切圆的半径是( )
A.1 B.2 C.3 D.4
10.如图,在直角坐标系中,等边△OAB的边OB在x轴的正半轴上,点A(3,m)(m>0),点M,N分别从B、O出发,以相同的速度,沿BO,OA向O、A运动,连接AM、BN交于点E,点P是y轴上一点,则当EP最小时,点P的坐标是( )
A.(0,) B.(0,2) C.(0,3) D.(0,)
二、填空题
11.中,,,,则的外接圆半径长是________.
12.为半圆O的直径,C为半圆弧的一个三等分点,过B,C两点的半圆O的切线交于点P,则________.
13.中,,,点是的外心,则的长为______.
14.如图,PA、PB是⊙O的切线,切点分别为A、B,若OA=2,∠P=60°,则AB的长为________
15.如图,AB是⊙O的直径,AC是⊙O的切线,连接OC交⊙O于点D,连接BD,∠B=25 ,则∠C的度数是_______.
三、解答题
16.如图,为的直径,,交于点C,于D.
(1)求证:直线是的切线;
(2)若,求的长.
17.如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC于点D,交BC于点E,过点E作EF⊥AC于点F,交AB的延长线于点P.
(1)求证:PE是⊙O的切线;
(2)若⊙O的直径为5,tanC=2,求BP的长.
18.如图,是的半径,且,是半圆上一点,连接,作,过点作半圆的切线,交的延长线于点,切点为,连接.
(1)当∥时,求证:;
(2)当 度时,为菱形.
19.如图,在中,直径与弦相交于点,.
(Ⅰ)如图①,若,求和的大小;
(Ⅱ)如图②,若,过点作的切线,与的延长线相交于点.求的大小.
20.如图,是的外接圆,切于点,与直径的延长线相交于点.
(Ⅰ)如图①,若,求的大小;
(Ⅱ)如图②,当,时,求的大小和的半径.
21.如图,为的直径,点C在上,点D为线段的延长线上一点,连接,过点O作交延长线于点E,交于点F,且满足.
(1)求证:是的切线;
(2)若,,求的长.
22.已知,内接于,.
(1)如图①,过点作射线交于点,若,求的度数.
(2)如图②,分别过点、点作的切线相交于点,若,求的度数.
23.我们将能完全覆盖某平面图形的最小圆称为该平面图形的最小覆盖圆.例如线段的最小覆盖圆就是以线段为直径的圆.锐角三角形的最小覆盖圆是该三角形的外接圆.
(1)分别在图1,图2中作出的最小覆盖圆.(要求尺规作图,保留作图痕迹,不写作法);
(2)根据(1)中的作图,钝角三角形的最小覆盖圆是______;
某地要修建一个基站,服务四个村庄E、F、G、H(其位置如图3所示),为使信号可以覆盖四个村庄,且基站所需发射功率最小(距离越小,所需功率越小),此基站应建在何处?请说明理由.
【参考答案】
1.C 2.B 3.C 4.C 5.B 6.C 7.C 8.A 9.C 10.B
11.
12.或
13.
14.
15.40°
16.解:(1)证明:连接,如图,
∵,
∴,
∵,
∴,
∴;
∵,
∴,
∴,
∴,
∴,
又∴是的半径,
∴直线是的切线.
(2)解:连接,
∵为直径,
∴,
∴,
∵,
∴,
∵,
∴.
17.解:(1)证明:连接,,
,
,
,
,
,
,
,
,
是的切线;
(2)为的直径,
,AB=AC=5,
,
,
设,,
,
,
(负值舍去),
,,
,
,
,
,
,
,
,
,
,
,
,
.
18.(1)证明:延长CB交AP于点F,连接OB、OE,
∵AD⊥AO,AD∥BC,
∴CF⊥AP,
∵BE∥AP,CF⊥AP,
∴CB⊥BE,即∠CBE=90°,
∵CE是⊙O的切线,则∠OEP=90°=∠CBE,
∵四边形ABCD是平行四边形,
∴AD=BC=AO=OE,
∵BE∥AP,
∴∠P=∠CEB,
在△CBE和△OEP中,
,
∴△CBE≌△OEP(AAS),
∴CE=OP;
(2)解:∵ ABCD为菱形,
∴DA=AB=AO=OB,
∴△BAO为等边三角形,
∴∠BAP等于60度时, ABCD为菱形,
故答案为:60.
19.解:(Ⅰ)∵,
∴∠C=
∴
∵直径与弦相交于点,
∴∠ADB=90°,
又∵
∴
(Ⅱ)∵
∴∠AEC=90°
又∵
∴
∴
∵是的切线
∴
∴
20.解:(Ⅰ)连接.
∵切于点,
∴,∴,
∵,
∴,
∴.
(Ⅱ)连接,设.
∵,∴,
∵,∴,
∴.
∵是的切线,
∴,即,
在中,,
即,
解得,
∴.
在中,,
∵,
∴,
∵,
∴,即的半径为2.
21.解:(1)连接OC,如图所示:
∵AB为⊙O的直径,
∴∠ACB=∠ACO+∠OCB=90°,
∵OB,OC是⊙O的半径,
∴OB=OC,
∴∠B=∠OCB,
∴∠ACO+∠B=90°,
∵OE∥AC,
∴∠ACD=∠E,
∵∠B=∠E,
∴∠ACD=∠B,
∴∠ACO+∠ACD=90°,即∠OCD=90°,即OC⊥CD,
∴CD是圆O的切线;
(2)∵AB=8,AC=4,
∴OC=AC=4,
又∵∠ACB=∠OCE=90°,∠B=∠E,
∴△ACB≌△OCE(AAS),
∴AB=OE=8,
∵OE∥AC,点O为AB中点,
∴OF=AC=2,
∴EF=OE-OF=6.
22.(1)解:∵四边形是的内接四边形,
∴,
∵,
∴,
∵,
∴,
∵,
∴,
∴;
(2)解:连结、,
∵、与相切于点、,
∴,,
∴,,
∵,,
∴,
∴,
∵,
∴,
∴;
23.(1)作图如下图所示;
(2)以最长边为直径的圆;
理由:∵线段的最小覆盖圆就是以线段为直径的圆,
由于∠A为钝角,因此∠A在圆内,
∴该圆为能完全覆盖该钝角三角形的最小圆.
(3)的外心(外接圆的圆心)
理由:如图,的外接圆刚好覆盖E,F,H三点,与直线交于点D,连接DH和DF
∵,
且,
∴,
∵∠HGF=50°+60°=110°,
∴.
∴点G在点E,D之间.
即点G被外接圆覆盖,
此时该圆为能完全覆盖该四边形的最小圆.
因此,此基站应建在的外心处.
同课章节目录
