2021——2022学年 人教版九年级数学上册24.3正多边形和圆 同步练习题(Word版含答案)
文档属性
| 名称 | 2021——2022学年 人教版九年级数学上册24.3正多边形和圆 同步练习题(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 400.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-30 23:24:27 | ||
图片预览


文档简介
2021——2022学年度人教版九年级数学上册 第二十四章 圆 24.3正多边形和圆 课后练习题
一、选择题
1.一个正八边形中最长的对角线等于a,最短的对角线等b,则这个正八边形的面积为( )
A.a2+b2 B.a2﹣b2 C.a+b D.ab
2.的内接多边形周长为,的外切多边形周长为,则下列各数中与此圆的周长最接近的是
A. B. C. D.
3.下列命题:①垂直于弦的直径平分弦,并且平分弦所对的两条弧;②在同圆或等圆中相等的圆心角所对的弧相等;③在同圆或等圆中如果两条弦相等,那么它们所对的圆心角相等;④圆内接四边形的对角互补.其中正确的命题共有( )
A.个 B.个 C.个 D.个
4.如图,PA、PB是⊙O的切线,A、B为切点,∠APB=40°,点C是⊙O上不同于A,B的任意一点,则∠ACB的度数为( )
A.70° B.40° C.110° D.70°或110°
5.如图,AB、AC是⊙O的切线,B、C为切点,∠A=50°,点P是圆上异于B、C的点,则∠BPC的度数是( )
A.65° B.115° C.115°或65° D.130°或65°
6.如图,在⊙O中,OA=AB,OC⊥AB,则下列结论错误的是( )
A.弦AB的长等于圆内接正六边形的边长 B.弦AC的长等于圆内接正十二边形的边长
C.AC=BC D.∠BAC=30°
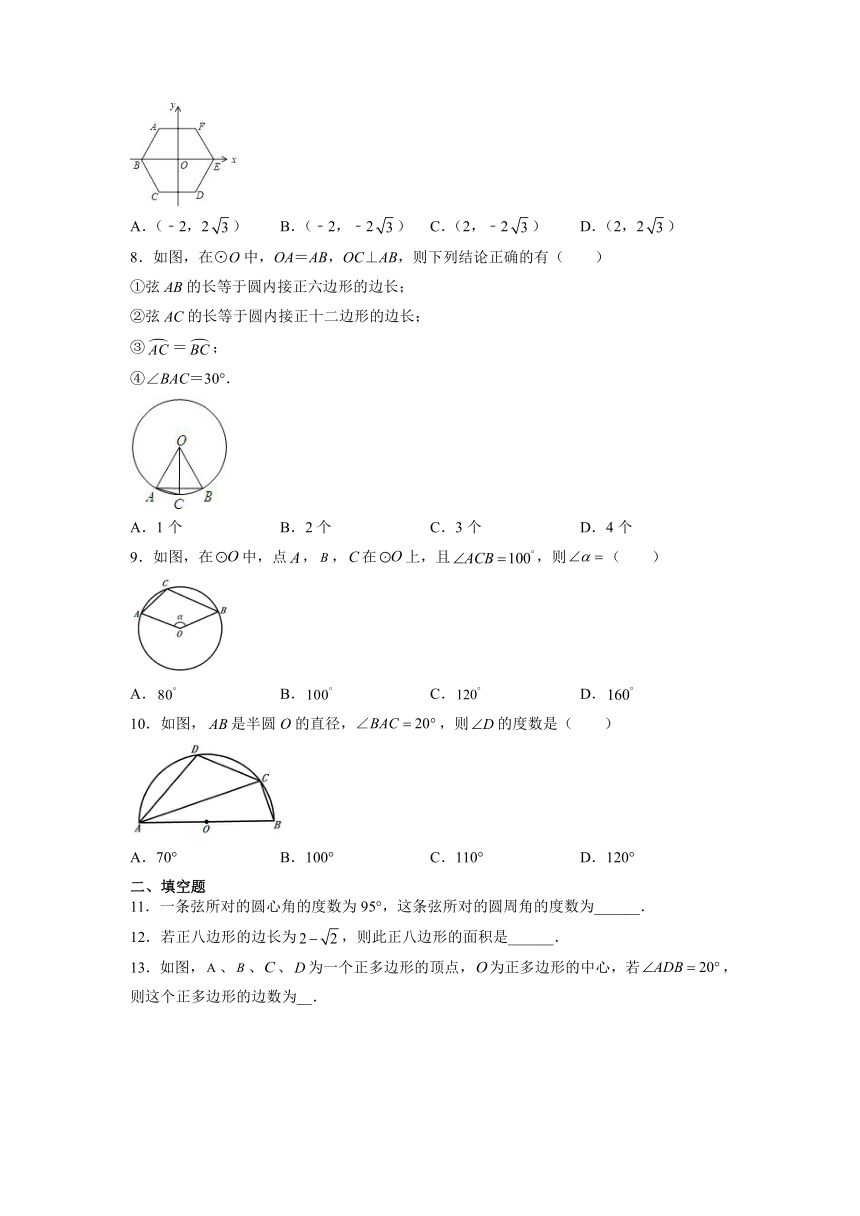
7.如图,边长为4的正六边形ABCDEF的中心与坐标原点O重合,AF∥x轴,将正六边形ABCDEF绕原点O顺时针旋转n次,每次旋转60°,当n=2020时,顶点A的坐标为( )
A.(﹣2,2) B.(﹣2,﹣2) C.(2,﹣2) D.(2,2)
8.如图,在⊙O中,OA=AB,OC⊥AB,则下列结论正确的有( )
①弦AB的长等于圆内接正六边形的边长;
②弦AC的长等于圆内接正十二边形的边长;
③=;
④∠BAC=30°.
A.1个 B.2个 C.3个 D.4个
9.如图,在中,点,,在上,且,则( )
A. B. C. D.
10.如图,是半圆O的直径,,则的度数是( )
A.70° B.100° C.110° D.120°
二、填空题
11.一条弦所对的圆心角的度数为95°,这条弦所对的圆周角的度数为______.
12.若正八边形的边长为,则此正八边形的面积是______.
13.如图,、、、为一个正多边形的顶点,为正多边形的中心,若,则这个正多边形的边数为__.
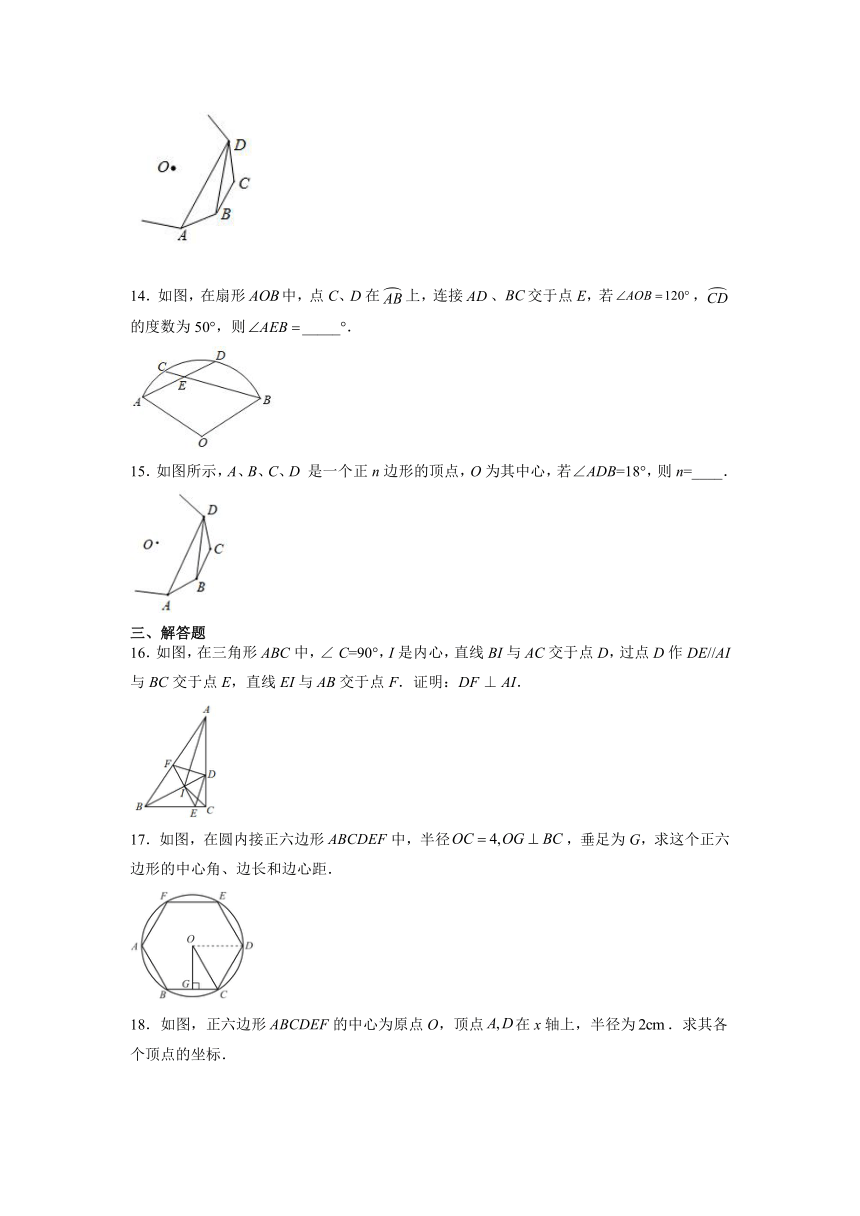
14.如图,在扇形中,点C、D在上,连接、交于点E,若,的度数为50°,则_____°.
15.如图所示,A、B、C、D 是一个正n边形的顶点,O为其中心,若∠ADB=18°,则n=____.
三、解答题
16.如图,在三角形ABC中,∠ C=90°,I是内心,直线BI与AC交于点D,过点D作DE//AI与BC交于点E,直线EI与AB交于点F.证明:DF ⊥ AI.
17.如图,在圆内接正六边形中,半径,垂足为G,求这个正六边形的中心角、边长和边心距.
18.如图,正六边形的中心为原点O,顶点在x轴上,半径为.求其各个顶点的坐标.
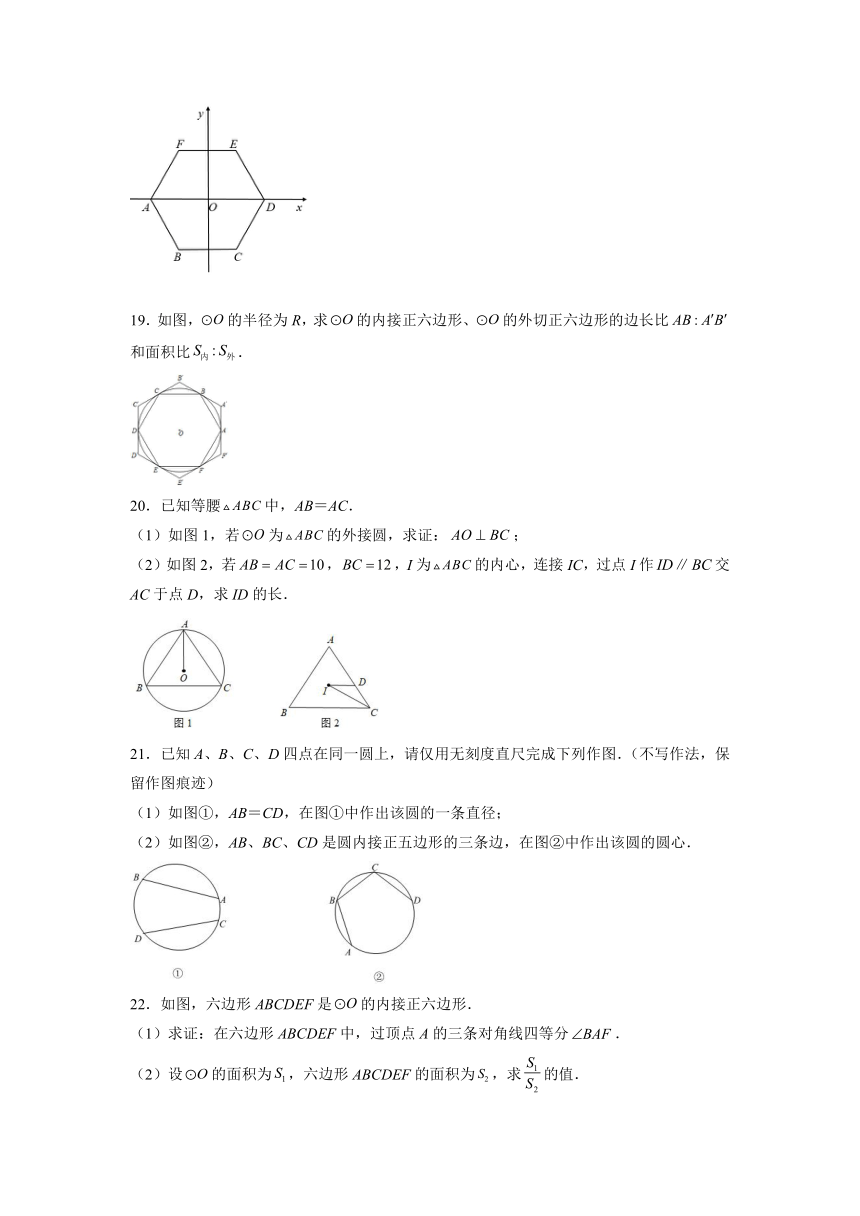
19.如图,的半径为R,求的内接正六边形、的外切正六边形的边长比和面积比.
20.已知等腰中,AB=AC.
(1)如图1,若为的外接圆,求证:;
(2)如图2,若,,I为的内心,连接IC,过点I作交AC于点D,求ID的长.
21.已知A、B、C、D四点在同一圆上,请仅用无刻度直尺完成下列作图.(不写作法,保留作图痕迹)
(1)如图①,AB=CD,在图①中作出该圆的一条直径;
(2)如图②,AB、BC、CD是圆内接正五边形的三条边,在图②中作出该圆的圆心.
22.如图,六边形ABCDEF是的内接正六边形.
(1)求证:在六边形ABCDEF中,过顶点A的三条对角线四等分.
(2)设的面积为,六边形ABCDEF的面积为,求的值.
23.如图M、N分别是⊙O的内接正三角形ABC、正方形ABCD、正五边形ABCDE、…、正n边形ABCDEFG…的边AB、BC上的点,且BM=CN,连接OM、ON
(1)求图1中∠MON的度数
(2)图2中∠MON的度数是 ,图3中∠MON的度数是
(3)试探究∠MON的度数与正n边形边数n的关系是____
【参考答案】
1.D 2.C 3.A 4.D 5.C 6.D 7.B 8.C 9.D 10.C
11.47.5°或132.5°.
12.
13.九
14.145
15.10
16.证明:∵是的外角,
∴,
∵,
∴,
而,
∴E、C、D、I四点共圆,
∴,
∴,
又 ,AI=AI,
∴△ADI≌△AFI (ASA),
∴,即是等腰三角形 ,且AI是顶角的角平分线,
∴.
17.解:连接,
∵六边形为正六边形,
∴.
∵ ,
∴为等边三角形.
∴,
∵六边形是正六边形,
∴ ,
∵,
∴,
在中,由勾股定理得:
∴.
∴正六边形的中心角为,边长为4,边心距为.
18.解:过点E作EG⊥x轴,垂足为G,连接OE,
∵OE=OD,∠EOD=,
∴△OED是正三角形,∠EOG=60°,∠OEG=30°,
∵OE=2cm,∠OGE=90°,
∴OG=OE=1cm,EG===cm,
点E的坐标为(1,),
又由题意知点D的坐标为(2,0),
由图形的对称性可知A(-2,0),B(-1,-),C(1,-),F(-1,).
故这个正六边形ABCDEF各个顶点的坐标分别为A(-2,0),B(-1,-),C(1,-),D(2,0),E(1,),F(-1,).
19.解:连接,如下图:
由正多边形的性质可得:,,
∴为等边三角形
∴,
由题意可得:,
∴
设,则,由勾股定理得
解得,
∵
∴,为的角平分线
∴
在中,,,解得
,
故;
20.(1)证明:连接OB、OC,∵AB=AC,
∴A在BC的垂直平分线上
又∵OB=OC,∴O也在BC的垂直平分线上
∴
(2)连接AI并延长交BC于点F,过点I分别作于点G,于点H
∵,I为的内心,∴,,
∴
设,由
可得:
∴
设,则,
∴
解得: 即
∵,平分
∴
∴设,
在中,
∴解得:
∴
21.解:(1)如图,EF即为所求;
(2)如图,点O即为所求.
22.解:(1)连接AE,AD,AC,
∵六边形ABCDEF是的内接正六边形,
∴EF=ED=CD=BC,
∴∠FAE=∠EAD=∠DAC=∠CAB,
即过顶点A的三条对角线四等分;
(2)过点O作OG⊥DE于G,连接OE,
设圆O的半径为r,
∴EF=BC=ED=r,AD=2r,
在正六边形ABCDEF中,
∠OED=∠ODE=60°,
∴∠EOG=30°,
∴EG=r,
∴OG==r,
∴正六边形ABCDEF的面积==,
圆O的面积=,
∴==.
23.(1)如图,连接OB、OC,则,
是内接正三角形,
中心角,
∵点O是内接正三角形ABC的内心,
∴,
∴,
在和中,,
∴,
∴,
∴,
故答案为:;
(2)如图1,连接OB、OC,
四边形ABCD是内接正方形,
中心角,
同(1)的方法可证:;
如图2,连接OB、OC,
五边形ABCDE是内接正五边形,
中心角,
同(1)的方法可证:,
故答案为:,;
(3)由上可知,的度数与正三角形边数的关系是,
的度数与正方形边数的关系是,
的度数与正五边形边数的关系是,
归纳类推得:的度数与正n边形边数n的关系是,
故答案为:.
一、选择题
1.一个正八边形中最长的对角线等于a,最短的对角线等b,则这个正八边形的面积为( )
A.a2+b2 B.a2﹣b2 C.a+b D.ab
2.的内接多边形周长为,的外切多边形周长为,则下列各数中与此圆的周长最接近的是
A. B. C. D.
3.下列命题:①垂直于弦的直径平分弦,并且平分弦所对的两条弧;②在同圆或等圆中相等的圆心角所对的弧相等;③在同圆或等圆中如果两条弦相等,那么它们所对的圆心角相等;④圆内接四边形的对角互补.其中正确的命题共有( )
A.个 B.个 C.个 D.个
4.如图,PA、PB是⊙O的切线,A、B为切点,∠APB=40°,点C是⊙O上不同于A,B的任意一点,则∠ACB的度数为( )
A.70° B.40° C.110° D.70°或110°
5.如图,AB、AC是⊙O的切线,B、C为切点,∠A=50°,点P是圆上异于B、C的点,则∠BPC的度数是( )
A.65° B.115° C.115°或65° D.130°或65°
6.如图,在⊙O中,OA=AB,OC⊥AB,则下列结论错误的是( )
A.弦AB的长等于圆内接正六边形的边长 B.弦AC的长等于圆内接正十二边形的边长
C.AC=BC D.∠BAC=30°
7.如图,边长为4的正六边形ABCDEF的中心与坐标原点O重合,AF∥x轴,将正六边形ABCDEF绕原点O顺时针旋转n次,每次旋转60°,当n=2020时,顶点A的坐标为( )
A.(﹣2,2) B.(﹣2,﹣2) C.(2,﹣2) D.(2,2)
8.如图,在⊙O中,OA=AB,OC⊥AB,则下列结论正确的有( )
①弦AB的长等于圆内接正六边形的边长;
②弦AC的长等于圆内接正十二边形的边长;
③=;
④∠BAC=30°.
A.1个 B.2个 C.3个 D.4个
9.如图,在中,点,,在上,且,则( )
A. B. C. D.
10.如图,是半圆O的直径,,则的度数是( )
A.70° B.100° C.110° D.120°
二、填空题
11.一条弦所对的圆心角的度数为95°,这条弦所对的圆周角的度数为______.
12.若正八边形的边长为,则此正八边形的面积是______.
13.如图,、、、为一个正多边形的顶点,为正多边形的中心,若,则这个正多边形的边数为__.
14.如图,在扇形中,点C、D在上,连接、交于点E,若,的度数为50°,则_____°.
15.如图所示,A、B、C、D 是一个正n边形的顶点,O为其中心,若∠ADB=18°,则n=____.
三、解答题
16.如图,在三角形ABC中,∠ C=90°,I是内心,直线BI与AC交于点D,过点D作DE//AI与BC交于点E,直线EI与AB交于点F.证明:DF ⊥ AI.
17.如图,在圆内接正六边形中,半径,垂足为G,求这个正六边形的中心角、边长和边心距.
18.如图,正六边形的中心为原点O,顶点在x轴上,半径为.求其各个顶点的坐标.
19.如图,的半径为R,求的内接正六边形、的外切正六边形的边长比和面积比.
20.已知等腰中,AB=AC.
(1)如图1,若为的外接圆,求证:;
(2)如图2,若,,I为的内心,连接IC,过点I作交AC于点D,求ID的长.
21.已知A、B、C、D四点在同一圆上,请仅用无刻度直尺完成下列作图.(不写作法,保留作图痕迹)
(1)如图①,AB=CD,在图①中作出该圆的一条直径;
(2)如图②,AB、BC、CD是圆内接正五边形的三条边,在图②中作出该圆的圆心.
22.如图,六边形ABCDEF是的内接正六边形.
(1)求证:在六边形ABCDEF中,过顶点A的三条对角线四等分.
(2)设的面积为,六边形ABCDEF的面积为,求的值.
23.如图M、N分别是⊙O的内接正三角形ABC、正方形ABCD、正五边形ABCDE、…、正n边形ABCDEFG…的边AB、BC上的点,且BM=CN,连接OM、ON
(1)求图1中∠MON的度数
(2)图2中∠MON的度数是 ,图3中∠MON的度数是
(3)试探究∠MON的度数与正n边形边数n的关系是____
【参考答案】
1.D 2.C 3.A 4.D 5.C 6.D 7.B 8.C 9.D 10.C
11.47.5°或132.5°.
12.
13.九
14.145
15.10
16.证明:∵是的外角,
∴,
∵,
∴,
而,
∴E、C、D、I四点共圆,
∴,
∴,
又 ,AI=AI,
∴△ADI≌△AFI (ASA),
∴,即是等腰三角形 ,且AI是顶角的角平分线,
∴.
17.解:连接,
∵六边形为正六边形,
∴.
∵ ,
∴为等边三角形.
∴,
∵六边形是正六边形,
∴ ,
∵,
∴,
在中,由勾股定理得:
∴.
∴正六边形的中心角为,边长为4,边心距为.
18.解:过点E作EG⊥x轴,垂足为G,连接OE,
∵OE=OD,∠EOD=,
∴△OED是正三角形,∠EOG=60°,∠OEG=30°,
∵OE=2cm,∠OGE=90°,
∴OG=OE=1cm,EG===cm,
点E的坐标为(1,),
又由题意知点D的坐标为(2,0),
由图形的对称性可知A(-2,0),B(-1,-),C(1,-),F(-1,).
故这个正六边形ABCDEF各个顶点的坐标分别为A(-2,0),B(-1,-),C(1,-),D(2,0),E(1,),F(-1,).
19.解:连接,如下图:
由正多边形的性质可得:,,
∴为等边三角形
∴,
由题意可得:,
∴
设,则,由勾股定理得
解得,
∵
∴,为的角平分线
∴
在中,,,解得
,
故;
20.(1)证明:连接OB、OC,∵AB=AC,
∴A在BC的垂直平分线上
又∵OB=OC,∴O也在BC的垂直平分线上
∴
(2)连接AI并延长交BC于点F,过点I分别作于点G,于点H
∵,I为的内心,∴,,
∴
设,由
可得:
∴
设,则,
∴
解得: 即
∵,平分
∴
∴设,
在中,
∴解得:
∴
21.解:(1)如图,EF即为所求;
(2)如图,点O即为所求.
22.解:(1)连接AE,AD,AC,
∵六边形ABCDEF是的内接正六边形,
∴EF=ED=CD=BC,
∴∠FAE=∠EAD=∠DAC=∠CAB,
即过顶点A的三条对角线四等分;
(2)过点O作OG⊥DE于G,连接OE,
设圆O的半径为r,
∴EF=BC=ED=r,AD=2r,
在正六边形ABCDEF中,
∠OED=∠ODE=60°,
∴∠EOG=30°,
∴EG=r,
∴OG==r,
∴正六边形ABCDEF的面积==,
圆O的面积=,
∴==.
23.(1)如图,连接OB、OC,则,
是内接正三角形,
中心角,
∵点O是内接正三角形ABC的内心,
∴,
∴,
在和中,,
∴,
∴,
∴,
故答案为:;
(2)如图1,连接OB、OC,
四边形ABCD是内接正方形,
中心角,
同(1)的方法可证:;
如图2,连接OB、OC,
五边形ABCDE是内接正五边形,
中心角,
同(1)的方法可证:,
故答案为:,;
(3)由上可知,的度数与正三角形边数的关系是,
的度数与正方形边数的关系是,
的度数与正五边形边数的关系是,
归纳类推得:的度数与正n边形边数n的关系是,
故答案为:.
同课章节目录
