人教版数学七年级下册 7.1.2_平面直角坐标系(第二课时)新 课件(35张ppt)
文档属性
| 名称 | 人教版数学七年级下册 7.1.2_平面直角坐标系(第二课时)新 课件(35张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-31 10:22:36 | ||
图片预览




文档简介
(共35张PPT)
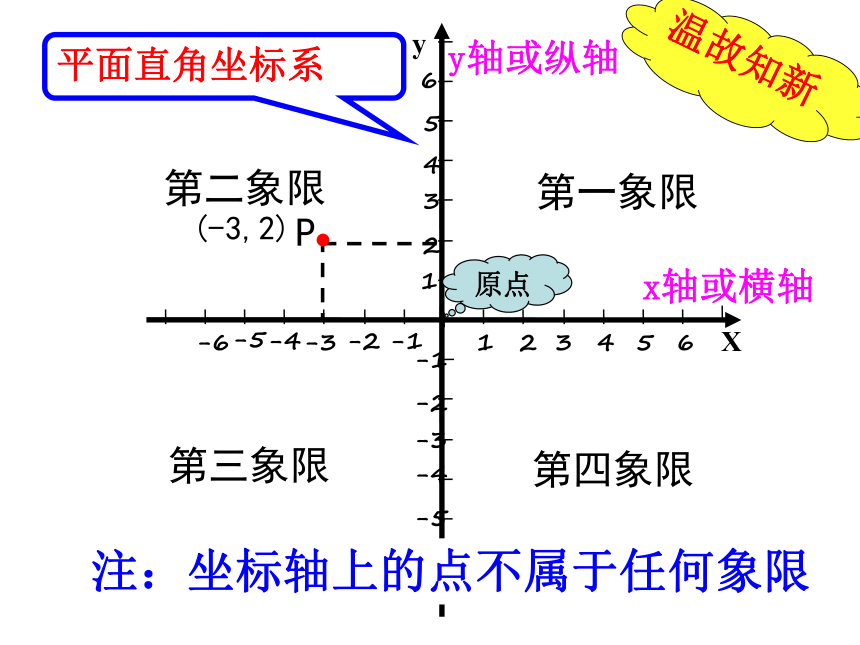
平面直角坐系
(第二课时)
7.1.2
y
5
-5
-2
-3
-4
-1
2
4
3
1
-6
6
-5
5
-3
-4
4
-2
3
-1
2
1
-6
6
X
x轴或横轴
y轴或纵轴
平面直角坐标系
第一象限
第二象限
第三象限
第四象限
P
(-3,2)
原点
注:坐标轴上的点不属于任何象限
温故知新
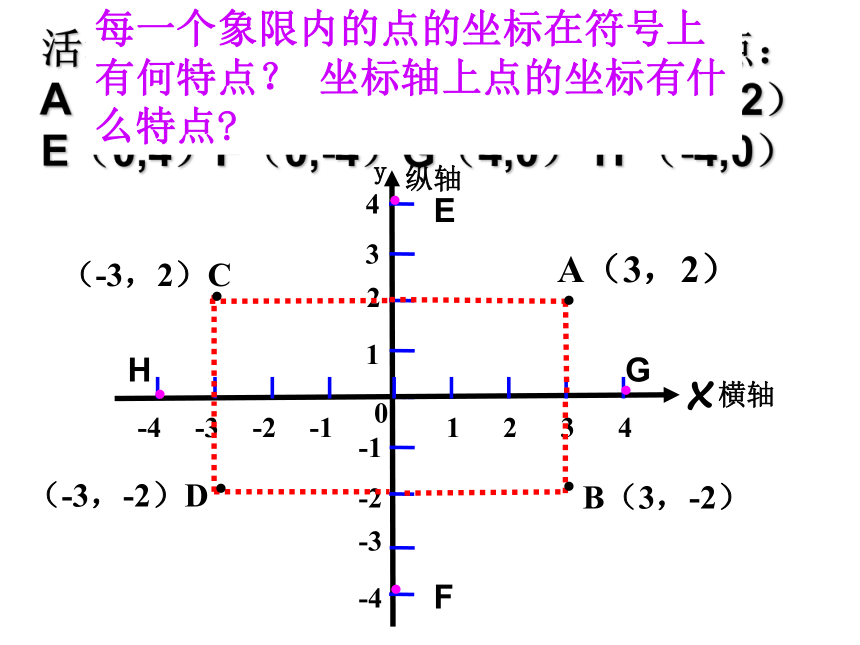
活动1:在直角坐标系中描出下列各点:A(3,2)B(3,-2)C(-3,2)D(-3,-2) E(0,4)F(0,-4)G(4,0) H (-4,0)
(-3,-2)D
3
1
4
2
-2
-4
-1
-3
0
1
2
3
4
-4
-3
-2
-1
x
横轴
y
纵轴
·
(-3,2)C
·
B(3,-2)
·
A(3,2)
E
·
·
F
·
G
·
H
·
每一个象限内的点的坐标在符号上有何特点? 坐标轴上点的坐标有什么特点
探究1
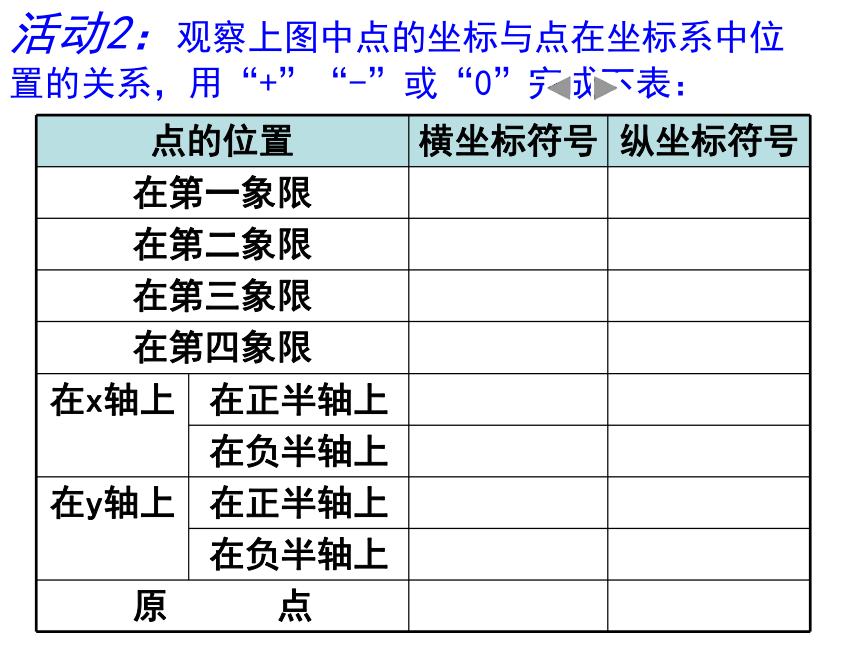
点的位置 横坐标符号 纵坐标符号
在第一象限 + +
在第二象限 - +
在第三象限 - -
在第四象限 + -
在x轴上 在正半轴上 + 0
在负半轴上 - 0
在y轴上 在正半轴上 0 +
在负半轴上 0 -
原 点 0 0
活动2:观察上图中点的坐标与点在坐标系中位置的关系,用“+”“-”或“0”完成下表:
第一、二、三、四象限内的坐标的
符号分别是(+,+),(-,+),(-,-),(+, -)
★ 坐标轴上的点坐标特点:
横轴上的点的纵坐标为0,表示为(x,0)
纵轴上的点的横坐标为0.表示为(0,y) 原点的坐标为(0,0)
★ 象限中点的坐标符号的特点:
讨 论:
5
-5
-2
-4
-1
2
4
1
-6
6
y
-5
5
-3
-4
4
-2
3
-1
2
1
-6
6
o
X
x轴或横轴
y轴或纵轴
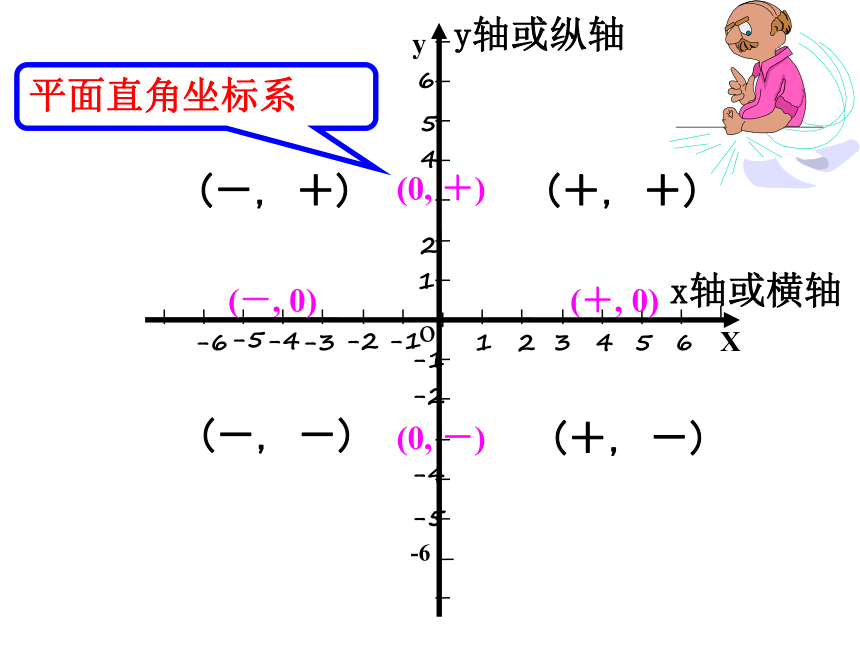
平面直角坐标系
(+, +)
(-, +)
(-, -)
(+, -)
(0, +)
(0, -)
(+, 0)
(-, 0)
C(3,4)
A(4,-2)
B(0,3)
D(-4,-3)
E(-2,0)
F(-4,3)
注:坐标轴上的点不属于任何象限
分别说出下列各点在哪个象限内或在哪条坐标轴上
试一试
B
C
D
A
x
y
0
(-3, -2 )
( -3 , 2)
( 3, 2 )
( 3 , -2)
1
1
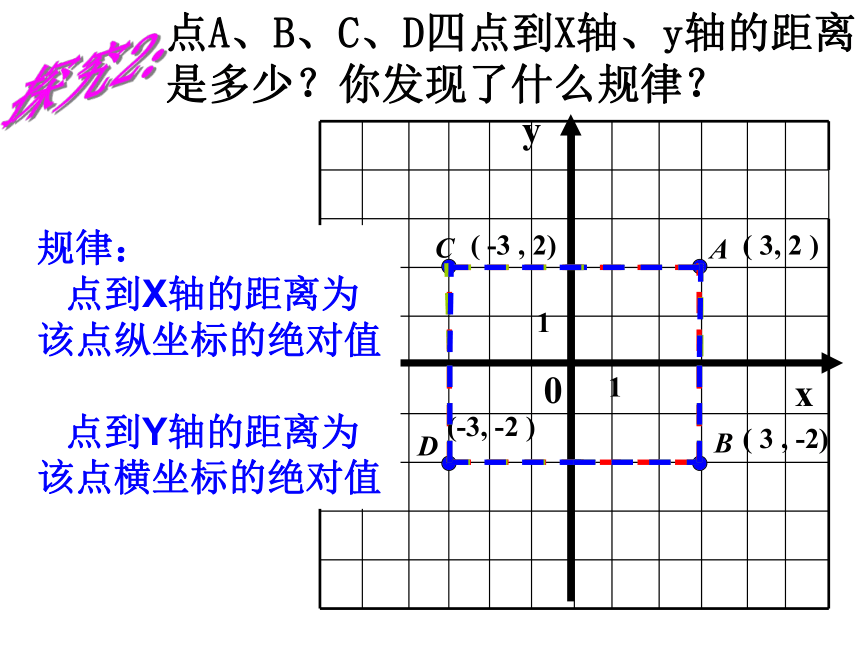
点A、B、C、D四点到X轴、y轴的距离是多少?你发现了什么规律?
规律:
点到X轴的距离为
该点纵坐标的绝对值
点到Y轴的距离为
该点横坐标的绝对值
请快速说出下列各个点到x轴、y轴的距离
A (4, -2) B (0, 3) C (3, 4)
D (-4,-3) E (-2, 0) F (-4, 3)
说一说
看一看
特点:两个图形关于直线对称
B
C
D
A
x
y
0
(-3, -2 )
( -3 , 2)
( 3, 2 )
( 3 , -2)
1
1
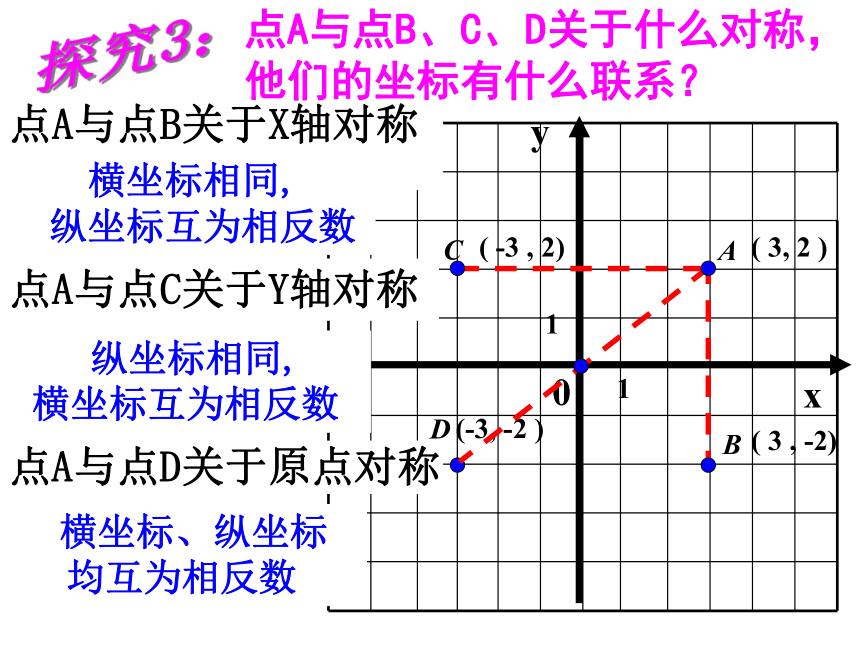
点A与点B关于X轴对称
横坐标相同,
纵坐标互为相反数
点A与点C关于Y轴对称
纵坐标相同,
横坐标互为相反数
点A与点D关于原点对称
横坐标、纵坐标
均互为相反数
点A与点B、C、D关于什么对称,他们的坐标有什么联系?
1
2
3
4
5
-4
-3
-2
-1
·
O
X
P(4,3)
·
B(4,-3)
A(-4,3)
C(-4,-3)
·
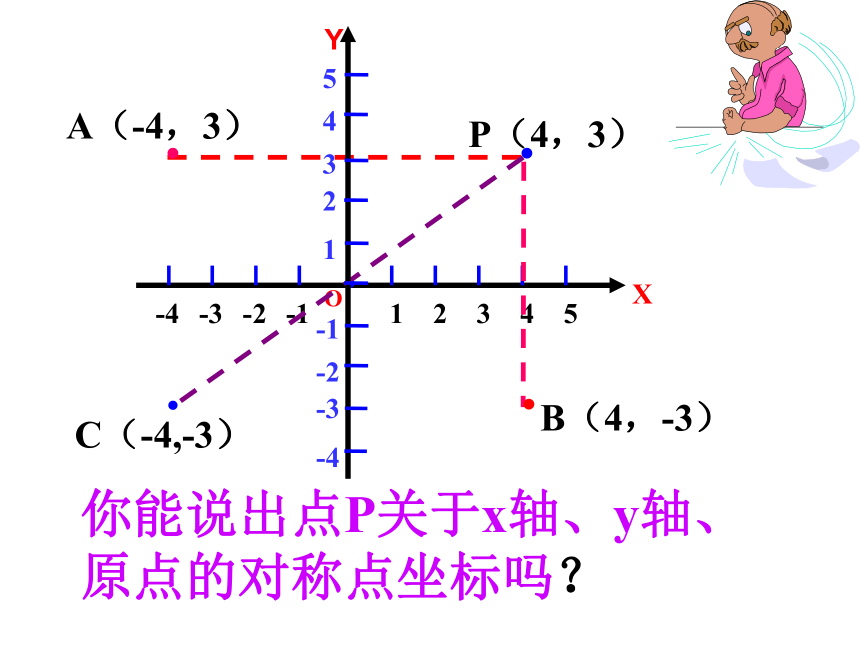
你能说出点P关于x轴、y轴、原点的对称点坐标吗?
·
3
1
4
2
5
-2
-4
-1
-3
·
Y
若设点M(a,b),
M点关于X轴的对称点M1( )
M点关于Y轴的对称点M2( )
M点关于原点O的对称点M3( )
a,-b
- a, b
-a,-b
练一练
你喜欢那种小动物?快来领一只
关于X轴、Y轴及原点对称的点的坐标特点
点到坐标轴的距离
点A(a,b)到X轴的距离为
点A(a,b)到Y轴的距离为
象限中点的坐标符号的情况及坐标轴上点坐标的特点
必做题:P45 4、6、10
选做题:P45 5、8、11
1.点(3,-2)在第_____象限;点(-1.5,-1)在第_______象限;点(0,3)在____轴上;
若点(a+1,-5)在y轴上,则a=______.
四
三
y
-1
知识互动点对典 :
2.点 M(- 8,12)到 x轴的距离是_______,到 y轴的距离是________.
12
8
知识互动点对典 :
3.点A(-2,4)关于x轴的对称点是_________ .
(-2,-4)
知识互动点对典 :
4.点A在x轴上,距离原点4个单位长度,则A点的坐标是_____________ 。
(4,0)或(-4,0)
方法探究一对一:
5.坐标平面内点P(m , 2)与点Q(3 , -2)关于原点对称,则 m =_____;
-3
方法探究一对一:
6.若点P在第三象限且到x轴的距离为 2 ,到y轴的距离为1.5,则点P的坐标是__________。
(-1.5,-2)
方法探究一对一:
7.点A(1-a,5),B(3 ,b)
关于y轴对称,则a=___,
b=____。
4
5
知能提升面对面:
8.在平面直角坐标系内,已知点P ( a , b ), 且a b < 0 , 则点P的位置在_____________。
第二或四象限
知能提升面对面:
9.实数 x,y满足 (x-1)2+ |y| = 0,则点 P( x,y)在【 】. (A)原点 (B)x轴正半轴
(C)第一象限 (D)任意位置
B
知能提升面对面:
1.点(3,-2)在第_____象限;点(-1.5,-1)
在第_______象限;点(0,3)在____轴上;
若点(a+1,-5)在y轴上,则a=______.
2.点 M(- 8,12)到 x轴的距离是_______,
到 y轴的距离是________.
3.点A(-2,4)关于x轴的对称点是 .
四
三
y
-1
12
8
(-2,-4)
知识互动点对典 :
4.点A在x轴上,距离原点4个单位长度,则A点的坐标是 。
5.坐标平面内点P(m , 2)与点Q(3 , -2)关于原点对称,则 m =_____;
(4,0)或(-4,0)
-3
6.若点P在第三象限且到x轴的距离为 2 ,到y轴的距离为1.5,则点P的坐标是__________。
(-1.5,-2)
方法探究一对一:
9.若点(a,b-1)在第二象限,则a的取值范围是_____,b的取值范围________。
10.实数 x,y满足 (x-1)2+ |y| = 0,则点 P( x,y)在【 】. (A)原点 (B)x轴正半轴
(C)第一象限 (D)任意位置
8.在平面直角坐标系内,已知点P ( a , b ), 且a b < 0 , 则点P的位置在_____________。
第二或四象限
a<0
b>1
B
7.点A(1-a,5),B(3 ,b)关于y轴对称,则a=___,b=____。
4
5
知能提升面对面:
4
5
4
5
关于坐标轴及原点对称的点的坐标的特点
关于X轴对称的两个点,横坐标相同, 纵坐标互为相反数
关于Y轴对称的两个点,纵坐标相同,横坐标互为相反数
关于原点对称的两个点,横坐标、纵坐标均互为相反数
结论:
·
C
活动2: 在直角坐标系中,描出下列各点:A(4,5),
B(-2,3),C(-4,-1),D(2.5,-2), E(0,-4)
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
·
B
·
D
·
A
E
·
(+,+)
(-,+)
(-,-)
(+,-)
每一个象限内的点的坐标在符号上有何 特点? 坐标轴上又有什么特点
在一次“寻宝”游戏中,寻宝人已经找到了坐标为
(3,2)和(3,-2)的两个标志点,并且知道藏宝
地点的坐标为(4,4),除此之外不知道其他信息,
如何确定直角坐标系找到“宝藏”?请跟同伴交流。
·
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
y
·
O
(3,-2)
X
(3,2)
·
·
(4,4)
考考你
7.如果同一直角坐标系下两个点的横坐标相同,那么过这两点的直线( ) (A)平行于x轴 (B)平行于y轴
(C)经过原点 (D)以上都不对
说一说
回顾与思考
1、什么是平面直角坐标系?
2、坐标轴分平面为四个部分,分别叫做什么?
3、如何求平面内点的坐标?
点的位置 横坐标符号 纵坐标符号
在第一象限 + +
在第二象限
在第三象限
在第四象限
在x轴上 在正半轴上
在负半轴上
在y轴上 在正半轴上
在负半轴上
原点
通过此例,你认为各象限符号有何规律?与同伴交流.
平面直角坐系
(第二课时)
7.1.2
y
5
-5
-2
-3
-4
-1
2
4
3
1
-6
6
-5
5
-3
-4
4
-2
3
-1
2
1
-6
6
X
x轴或横轴
y轴或纵轴
平面直角坐标系
第一象限
第二象限
第三象限
第四象限
P
(-3,2)
原点
注:坐标轴上的点不属于任何象限
温故知新
活动1:在直角坐标系中描出下列各点:A(3,2)B(3,-2)C(-3,2)D(-3,-2) E(0,4)F(0,-4)G(4,0) H (-4,0)
(-3,-2)D
3
1
4
2
-2
-4
-1
-3
0
1
2
3
4
-4
-3
-2
-1
x
横轴
y
纵轴
·
(-3,2)C
·
B(3,-2)
·
A(3,2)
E
·
·
F
·
G
·
H
·
每一个象限内的点的坐标在符号上有何特点? 坐标轴上点的坐标有什么特点
探究1
点的位置 横坐标符号 纵坐标符号
在第一象限 + +
在第二象限 - +
在第三象限 - -
在第四象限 + -
在x轴上 在正半轴上 + 0
在负半轴上 - 0
在y轴上 在正半轴上 0 +
在负半轴上 0 -
原 点 0 0
活动2:观察上图中点的坐标与点在坐标系中位置的关系,用“+”“-”或“0”完成下表:
第一、二、三、四象限内的坐标的
符号分别是(+,+),(-,+),(-,-),(+, -)
★ 坐标轴上的点坐标特点:
横轴上的点的纵坐标为0,表示为(x,0)
纵轴上的点的横坐标为0.表示为(0,y) 原点的坐标为(0,0)
★ 象限中点的坐标符号的特点:
讨 论:
5
-5
-2
-4
-1
2
4
1
-6
6
y
-5
5
-3
-4
4
-2
3
-1
2
1
-6
6
o
X
x轴或横轴
y轴或纵轴
平面直角坐标系
(+, +)
(-, +)
(-, -)
(+, -)
(0, +)
(0, -)
(+, 0)
(-, 0)
C(3,4)
A(4,-2)
B(0,3)
D(-4,-3)
E(-2,0)
F(-4,3)
注:坐标轴上的点不属于任何象限
分别说出下列各点在哪个象限内或在哪条坐标轴上
试一试
B
C
D
A
x
y
0
(-3, -2 )
( -3 , 2)
( 3, 2 )
( 3 , -2)
1
1
点A、B、C、D四点到X轴、y轴的距离是多少?你发现了什么规律?
规律:
点到X轴的距离为
该点纵坐标的绝对值
点到Y轴的距离为
该点横坐标的绝对值
请快速说出下列各个点到x轴、y轴的距离
A (4, -2) B (0, 3) C (3, 4)
D (-4,-3) E (-2, 0) F (-4, 3)
说一说
看一看
特点:两个图形关于直线对称
B
C
D
A
x
y
0
(-3, -2 )
( -3 , 2)
( 3, 2 )
( 3 , -2)
1
1
点A与点B关于X轴对称
横坐标相同,
纵坐标互为相反数
点A与点C关于Y轴对称
纵坐标相同,
横坐标互为相反数
点A与点D关于原点对称
横坐标、纵坐标
均互为相反数
点A与点B、C、D关于什么对称,他们的坐标有什么联系?
1
2
3
4
5
-4
-3
-2
-1
·
O
X
P(4,3)
·
B(4,-3)
A(-4,3)
C(-4,-3)
·
你能说出点P关于x轴、y轴、原点的对称点坐标吗?
·
3
1
4
2
5
-2
-4
-1
-3
·
Y
若设点M(a,b),
M点关于X轴的对称点M1( )
M点关于Y轴的对称点M2( )
M点关于原点O的对称点M3( )
a,-b
- a, b
-a,-b
练一练
你喜欢那种小动物?快来领一只
关于X轴、Y轴及原点对称的点的坐标特点
点到坐标轴的距离
点A(a,b)到X轴的距离为
点A(a,b)到Y轴的距离为
象限中点的坐标符号的情况及坐标轴上点坐标的特点
必做题:P45 4、6、10
选做题:P45 5、8、11
1.点(3,-2)在第_____象限;点(-1.5,-1)在第_______象限;点(0,3)在____轴上;
若点(a+1,-5)在y轴上,则a=______.
四
三
y
-1
知识互动点对典 :
2.点 M(- 8,12)到 x轴的距离是_______,到 y轴的距离是________.
12
8
知识互动点对典 :
3.点A(-2,4)关于x轴的对称点是_________ .
(-2,-4)
知识互动点对典 :
4.点A在x轴上,距离原点4个单位长度,则A点的坐标是_____________ 。
(4,0)或(-4,0)
方法探究一对一:
5.坐标平面内点P(m , 2)与点Q(3 , -2)关于原点对称,则 m =_____;
-3
方法探究一对一:
6.若点P在第三象限且到x轴的距离为 2 ,到y轴的距离为1.5,则点P的坐标是__________。
(-1.5,-2)
方法探究一对一:
7.点A(1-a,5),B(3 ,b)
关于y轴对称,则a=___,
b=____。
4
5
知能提升面对面:
8.在平面直角坐标系内,已知点P ( a , b ), 且a b < 0 , 则点P的位置在_____________。
第二或四象限
知能提升面对面:
9.实数 x,y满足 (x-1)2+ |y| = 0,则点 P( x,y)在【 】. (A)原点 (B)x轴正半轴
(C)第一象限 (D)任意位置
B
知能提升面对面:
1.点(3,-2)在第_____象限;点(-1.5,-1)
在第_______象限;点(0,3)在____轴上;
若点(a+1,-5)在y轴上,则a=______.
2.点 M(- 8,12)到 x轴的距离是_______,
到 y轴的距离是________.
3.点A(-2,4)关于x轴的对称点是 .
四
三
y
-1
12
8
(-2,-4)
知识互动点对典 :
4.点A在x轴上,距离原点4个单位长度,则A点的坐标是 。
5.坐标平面内点P(m , 2)与点Q(3 , -2)关于原点对称,则 m =_____;
(4,0)或(-4,0)
-3
6.若点P在第三象限且到x轴的距离为 2 ,到y轴的距离为1.5,则点P的坐标是__________。
(-1.5,-2)
方法探究一对一:
9.若点(a,b-1)在第二象限,则a的取值范围是_____,b的取值范围________。
10.实数 x,y满足 (x-1)2+ |y| = 0,则点 P( x,y)在【 】. (A)原点 (B)x轴正半轴
(C)第一象限 (D)任意位置
8.在平面直角坐标系内,已知点P ( a , b ), 且a b < 0 , 则点P的位置在_____________。
第二或四象限
a<0
b>1
B
7.点A(1-a,5),B(3 ,b)关于y轴对称,则a=___,b=____。
4
5
知能提升面对面:
4
5
4
5
关于坐标轴及原点对称的点的坐标的特点
关于X轴对称的两个点,横坐标相同, 纵坐标互为相反数
关于Y轴对称的两个点,纵坐标相同,横坐标互为相反数
关于原点对称的两个点,横坐标、纵坐标均互为相反数
结论:
·
C
活动2: 在直角坐标系中,描出下列各点:A(4,5),
B(-2,3),C(-4,-1),D(2.5,-2), E(0,-4)
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
·
B
·
D
·
A
E
·
(+,+)
(-,+)
(-,-)
(+,-)
每一个象限内的点的坐标在符号上有何 特点? 坐标轴上又有什么特点
在一次“寻宝”游戏中,寻宝人已经找到了坐标为
(3,2)和(3,-2)的两个标志点,并且知道藏宝
地点的坐标为(4,4),除此之外不知道其他信息,
如何确定直角坐标系找到“宝藏”?请跟同伴交流。
·
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
y
·
O
(3,-2)
X
(3,2)
·
·
(4,4)
考考你
7.如果同一直角坐标系下两个点的横坐标相同,那么过这两点的直线( ) (A)平行于x轴 (B)平行于y轴
(C)经过原点 (D)以上都不对
说一说
回顾与思考
1、什么是平面直角坐标系?
2、坐标轴分平面为四个部分,分别叫做什么?
3、如何求平面内点的坐标?
点的位置 横坐标符号 纵坐标符号
在第一象限 + +
在第二象限
在第三象限
在第四象限
在x轴上 在正半轴上
在负半轴上
在y轴上 在正半轴上
在负半轴上
原点
通过此例,你认为各象限符号有何规律?与同伴交流.
