人教版数学七年级下册 第五章相交线与平行线复习 课件(共116张PPT)
文档属性
| 名称 | 人教版数学七年级下册 第五章相交线与平行线复习 课件(共116张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-31 00:00:00 | ||
图片预览



文档简介
(共116张PPT)
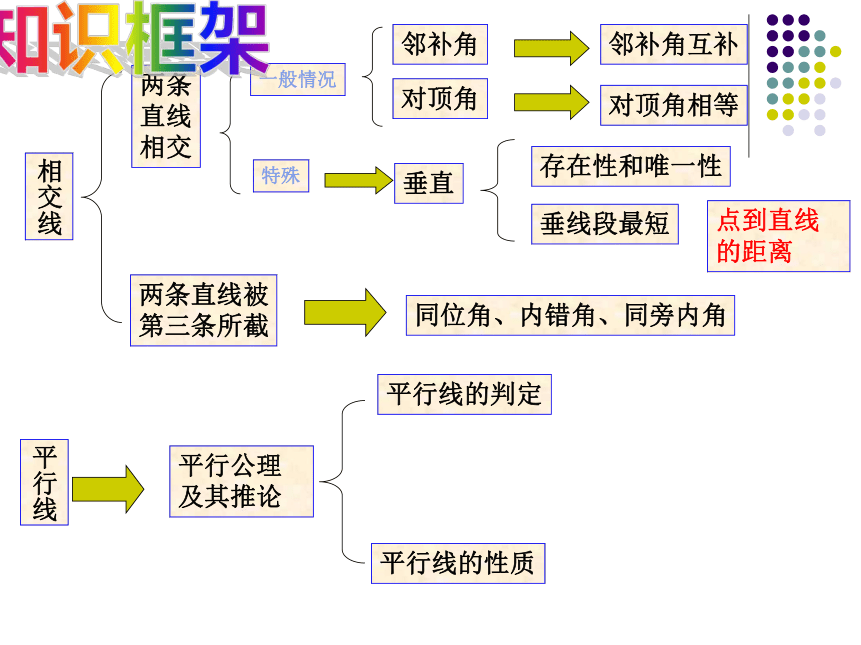
相交线
两条
直线
相交
两条直线被
第三条所截
一般情况
邻补角
对顶角
邻补角互补
对顶角相等
特殊
垂直
存在性和唯一性
垂线段最短
点到直线的距离
同位角、内错角、同旁内角
平行线
平行公理及其推论
平行线的判定
平行线的性质
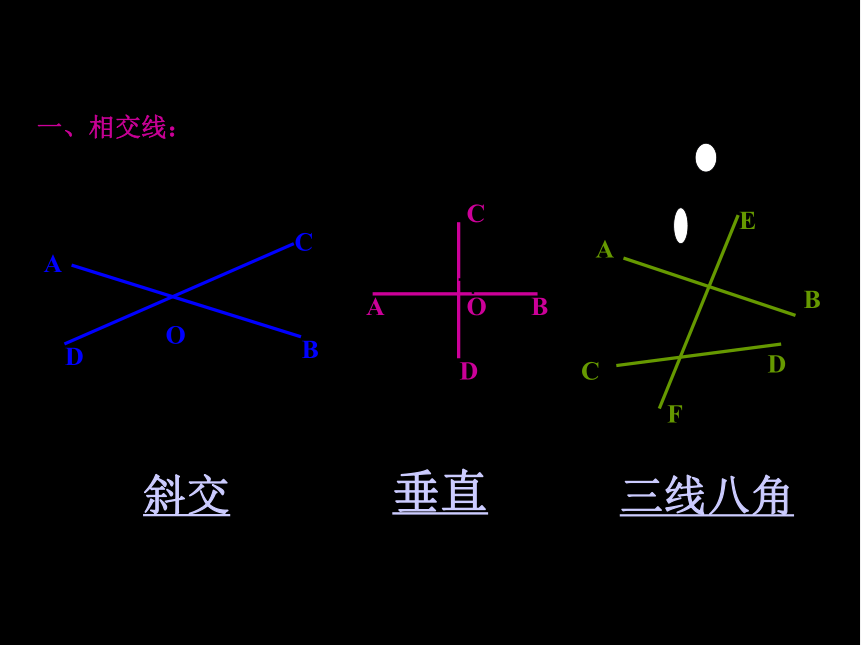
一、相交线:
A
B
C
D
O
A
B
C
D
O
7
2
4
A
B
C
D
E
F
1
3
5
6
8
垂直
斜交
三线八角
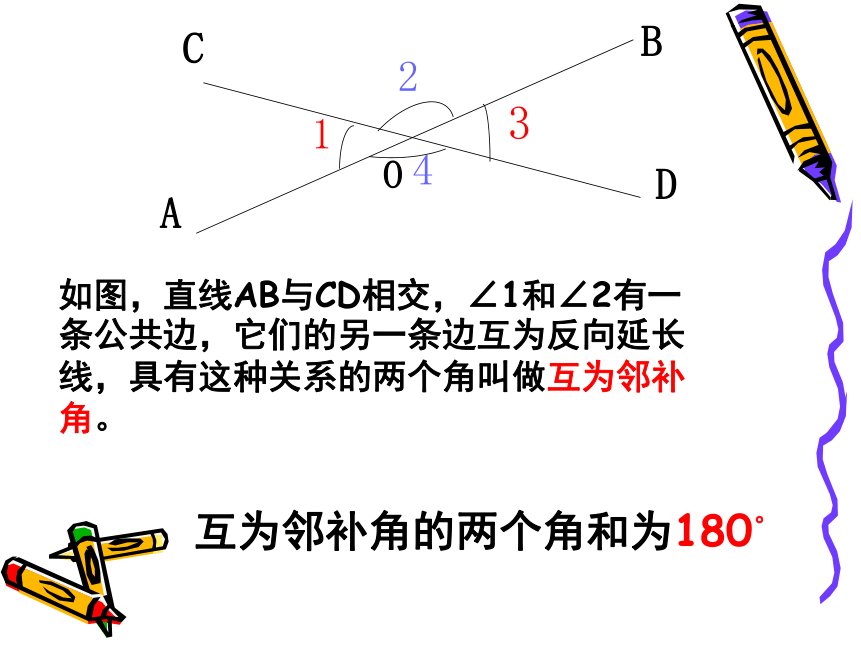
如图,直线AB与CD相交,∠1和∠2有一条公共边,它们的另一条边互为反向延长线,具有这种关系的两个角叫做互为邻补角。
互为邻补角的两个角和为180。
4
2
3
1
C
D
A
B
O
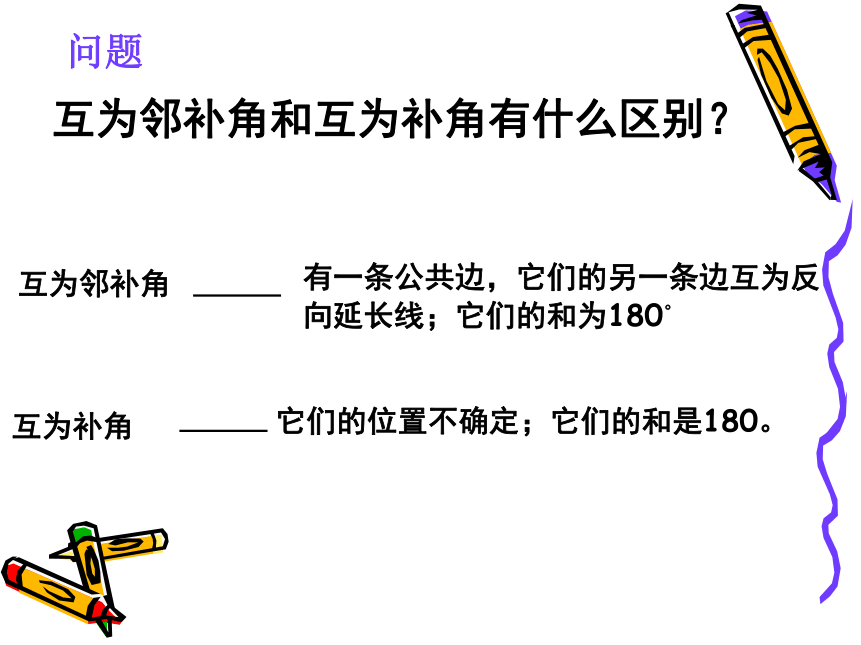
互为邻补角和互为补角有什么区别?
问题
互为邻补角
有一条公共边,它们的另一条边互为反向延长线;它们的和为180。
互为补角
它们的位置不确定;它们的和是180。
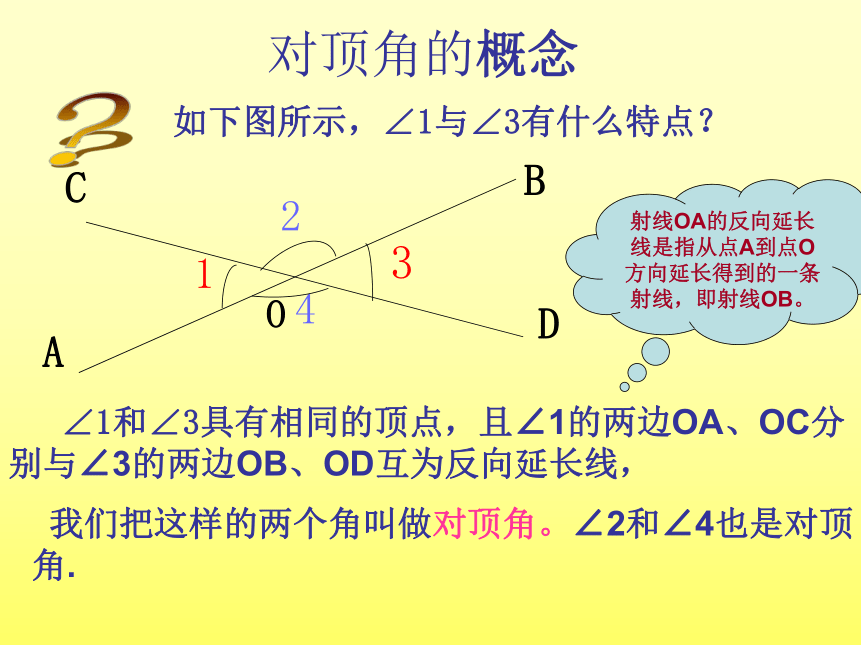
对顶角的概念
如下图所示,∠1与∠3有什么特点?
∠1和∠3具有相同的顶点,且∠1的两边OA、OC分别与∠3的两边OB、OD互为反向延长线,
4
2
3
1
C
D
A
B
O
射线OA的反向延长线是指从点A到点O方向延长得到的一条射线,即射线OB。
我们把这样的两个角叫做对顶角。∠2和∠4也是对顶角.
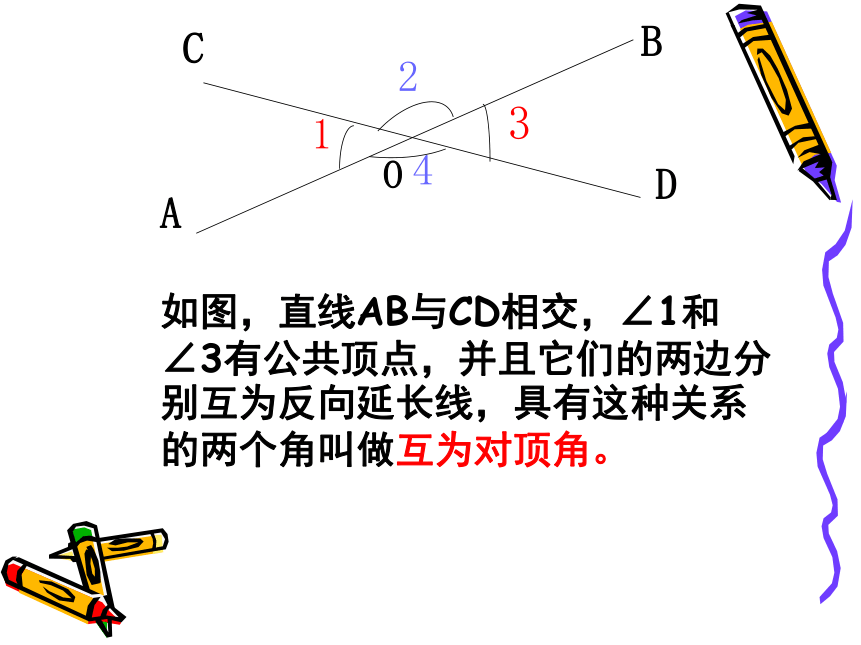
如图,直线AB与CD相交,∠1和∠3有公共顶点,并且它们的两边分别互为反向延长线,具有这种关系的两个角叫做互为对顶角。
4
2
3
1
C
D
A
B
O
猜想
1、对顶角在数量上有什么关系?
2、你可以用哪些方法进行验证?
O
A
B
C
D
)
(
1
3
4
2
)
(
已知:直线AB与CD相交于O点(如图),说明∠1=∠3、 ∠2=∠4的理由
解:∵直线AB与CD相交于O点,
∴∠1+∠2=180°、 ∠2+∠3=180°(邻补角的定义)
∴∠1=∠3(同角或等角的补角相等)
同理可得:∠2=∠4
对顶角相等
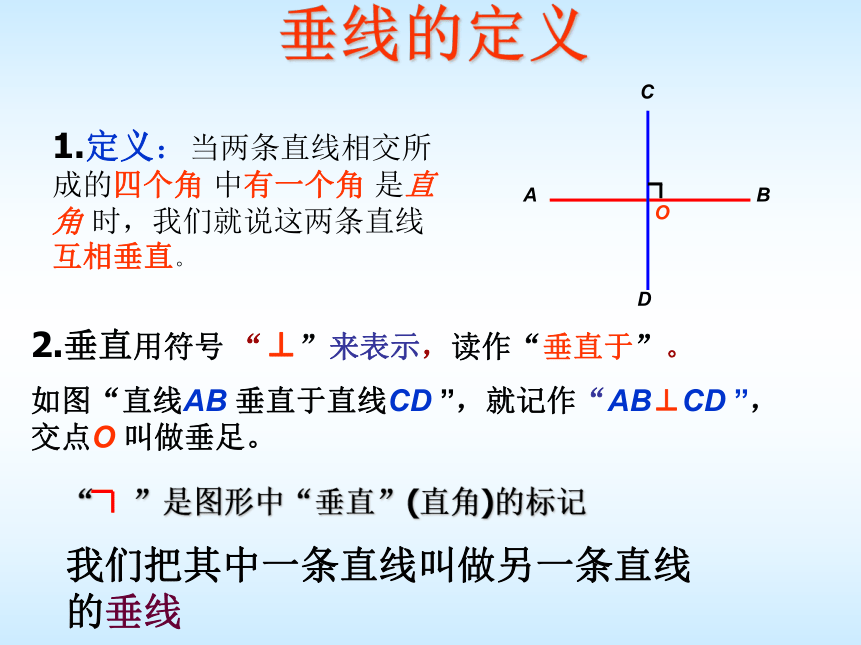
垂线的定义
2.垂直用符号 “⊥”来表示,读作“垂直于”。
如图“直线AB 垂直于直线CD ”,就记作“AB⊥CD ”,交点O 叫做垂足。
1.定义:当两条直线相交所成的四个角 中有一个角 是直角 时,我们就说这两条直线互相垂直。
O
A
B
C
D
“ ”是图形中“垂直”(直角)的标记
我们把其中一条直线叫做另一条直线的垂线
O
C
D
A
B
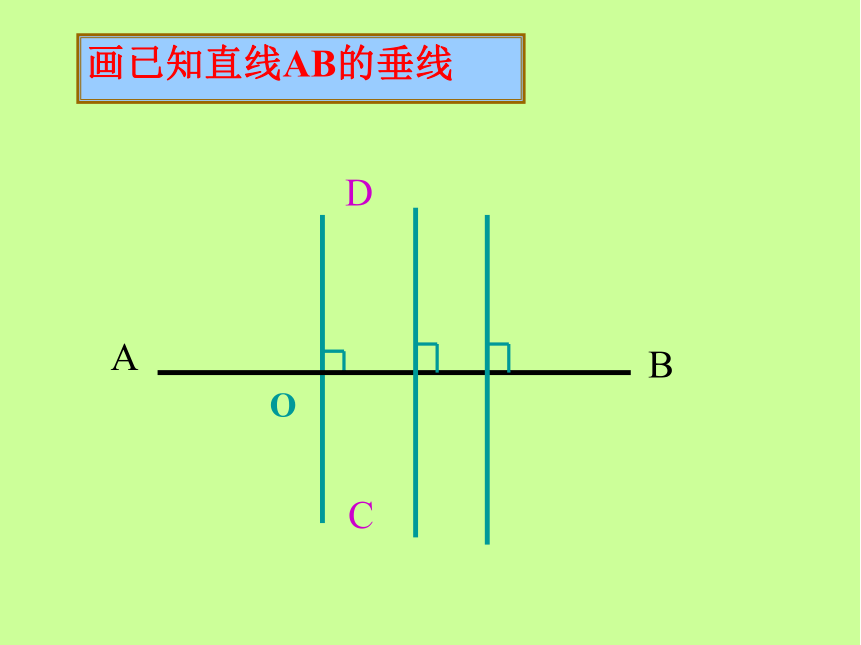
画已知直线AB的垂线
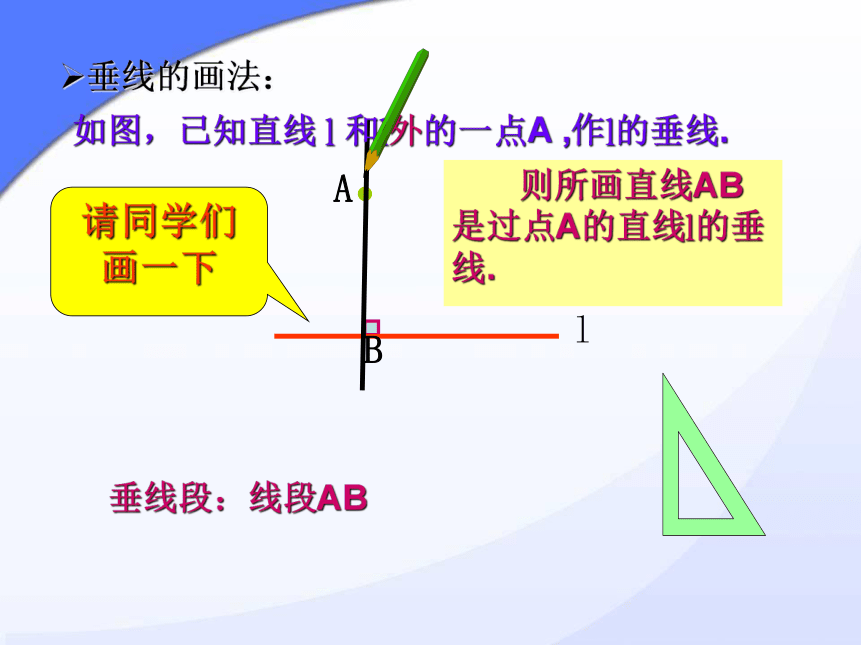
垂线的画法:
l
A
如图,已知直线 l 和l外的一点A ,作l的垂线.
B
则所画直线AB是过点A的直线l的垂线.
请同学们画一下
垂线段:线段AB
垂线的性质
P
从上面的画图过程中,你能得到什么结论?不妨说说看!
垂线的性质(1):平面内,过直线上一点或直线外一点有且只有一条直线与已知直线垂直。
A
P
B
A
B
过一点,有且只有一条直线与已知直线垂直。
线段、射线的垂线应怎么画呢?
A
B
P
Q
O
A
线段的延长线
或射线的反向延长线
A
B
C
D
O
(二)、垂直:
2、画法:
3、性质:
两条直线相交所形成的四个角中有一个是直角时叫两条直线互相垂直。
过一点画一条直线的垂线。
P
a
Q
(1)、过一点有且只有一条直线垂直于已知直线。
p
A
B
C
D
E
(2)、 垂线段最短。
点到直线的距离:
b
b
c
1、定义:
点到直线的距离: 从直线外一点到这条直线的 垂线段的长度,叫做这点到这条直线的距离.
判断:
1、画出点A到直线BC的距离。( )
2、画出点A到直线BC的垂线段。( )
3、量出点A到直线BC的距离。 ( )
4、垂线最短。 ( )
B
C
A
D
5、如图,AC⊥BC,CD ⊥AB,垂足分别是C点、D点。
(1)点B到CD的距离是线段______的长度;
(2)点C到AB的距离是线段______的长度;
(3)点A到CB的距离是线段______的长度。
A
B
C
D
BD
CD
AC
过一点画已知直线的垂线的方法
过一点画垂线的方法可归纳为“一靠、二过、三画、四标”
1.一靠:把三角板的一条直角边靠在已知直线上;
2.二过:让三角板的另一条直角边经过已知点;
A
B
P
3.三画:沿着已知点所在的直角边画直线;
∟
4.四标:标上直角符号“ ”。
P
如图,线段AB叫做点A到直线l 的垂线段,
注意他们的区别!
A
B
C
l
D
点到直线的距离:
直线外一点到直线的垂线段的长度,叫做点到直线的距离。
线段AB的长度就是点A到直线l 的距离
如图 ,已知AB. CD相交于O, OE⊥CD
于O,∠AOC=36°,则∠BOE= 。
(A)36°
(B) 64°
(C)144°
(D) 54°
A
B
O
C
D
E
54°
随堂练习
1、判断
1)一条直线的垂线只能画一条( )
2)两直线相交所构成的四个角相等,则这两直线互相垂直( )
3)点到直线的垂线段就是点到直线的距离( )
4)在同一平面内,过一点有且只有一条直线与已知直线垂直( )
×
√
×
√
3、如图:在铁路旁边有一张庄,现在要建一火车站,为了使张庄人乘火车最方便(即距离最近),请你在铁路上选一点来建火车站,并说明理由。
张庄
∟
P
小试牛刀
1、直线m外有点P,它到直线m上点A、B、C的距离分别是6厘米、3厘米、5厘米,则点P到直线m的距离( )
A等于6厘米. B.等于3厘米 C.等于5厘米 D.不大于3厘米
2、如右图,若OC⊥AB于点O,OE⊥OD,
则图中互余的角有( )
A. 4对 B. 3对 C. 2对 D. 1对
A
B
O
D
C
E
3、如右图,直线a、b、c相交于一点,若∠1 :∠2 :∠3=1 : 2 : 3,则∠2的度数为____度。 ∠3的度数为 _______度。直线a、b的位置关系是____________。
1
2
3
a
b
c
D
A
60
90
互相垂直
4、如右图,按要求完成下列各题:
m
A
B
⑴请画出由A地经过B地去河边m的最短路线;
⑵确定A地去B地的路线的依据是:___________________;
⑶确定B地去河边的路线的依据是:______________。
5、如图,直线AB和CD相交于点O,
OB平分∠DOF,
OE⊥AB,O为垂足,∠1=50°,
求∠AOC和∠COF的度数。
A
B
D
E
O
1
C
F
能力挑战:
C
两点之间,线段最短
垂线段最短
中考在线:【2008·四川乐山】
如图,直线l1与l2相交于点O,OM⊥l1,
若α=44°,则β=( )
l1
l2
O
M
α
β
46°
练习
一、下列叙述中不正确的是( )
(A)经过直外一点只能画一条已知道直线的垂线
(B)如果两条直线相交所构成的四个角中有三个角度相等,那么这两条直线一定垂直
(C)直线l上有三点A、B、C,在直线l个外有一点P,若PB(D)两条线段垂直是指这两条线段所在的直线垂直
C
二、一辆汽车在直线型公路AB 上由A向B行驶,M、N分别是位于公路两侧的村庄,设汽车行驶到P位置时离村庄M最近;行驶到Q位置时离村庄N最近,请在图中公路AB上分别画出P、Q两点的位置
A
B
M
N
·
·
∟
∟
P
Q
三、如图,直线AB与CD相交于点O,OE⊥CD, OF⊥AB,∠DOF=65o,求∠BOE和∠AOC的度数。
A
B
O
F
C
D
E
∵OE⊥CD, OF⊥AB (已知)
解:
∴ ∠BOF=∠DOE=90o(垂直的定义)
∴∠BOD=∠BOF-∠DOF
=90o-65o=25o
∴∠BOE=∠DOE-∠BOD=90o-25o=65o
而∠AOC=∠BOD=25o
(对顶角相等)
答: ∠BOE=65o,∠AOC=25o
A
B
C
D
E
F
1
2
3
4
5
6
7
8
同位角:
内错角:
同旁内角:
∠1与∠5; ∠4与∠8;
∠2与∠6; ∠3与∠7.
∠4与∠6; ∠3与∠5.
∠4与∠5; ∠3与∠6.
A
B
C
D
E
O
如图: ∠ A和哪个角是同位角
∠ A和哪个角是 内错角
∠ A和哪个角是同旁内角
(∠COE、 ∠COB)
(∠C、 ∠AOD)
(∠B 、 ∠AOB、 ∠AOE)
(三)、三线八角:
概念辨析
一、判断题
1、有公共顶点且相等的两个角是对顶角。( )
2、两条直线相交,有两组对顶角。 ( )
3、两条直线相交所构成的四个角中有一个角是直角,
那么其余的三个角也是直角。 ( )
二、选择题
1、如右图直线AB、CD交于点O,OE为射线,那么( )
A。∠AOC和∠BOE是对顶角;
B。∠COE和∠AOD是对顶角;
C。∠BOC和∠AOD是对顶角;
D。∠AOE和∠DOE是对顶角。
2、如右图中直线AB、CD交于O,
OE是∠BOC的平分线且∠BOE=50度,
那么∠AOE=( )度
(A)80;(B)100;(C)130(D)150。
A
B
C
D
O
E
×
√
√
C
C
A
C
B
D
E
F
如图:怎样描述这三条直线的位置关系?
直线AB、CD被EF所截
7
1
2
3
4
5
6
8
观察
截线
被截直线
观察
F
问题:1、观察∠1与∠5的位置关系
A
C
B
D
E
1
2
3
4
5
6
7
8
1
5
5
1
7
8
5
4
1
3
2
6
2
6
7
3
观察∠1和∠5两角:
F
5
1
7
8
5
4
1
3
2
6
2
6
7
3
5
1
各有一边在同一直线上
观察∠1和∠5两角:
5
1
7
8
5
4
1
3
2
6
2
6
7
3
两角在直线EF的同一侧
5
1
观察∠1和∠5两角:
E
F
5
1
7
8
5
4
1
3
2
6
2
6
7
3
两角分别在直线AB,CD同一方
5
1
观察∠1和∠5两角:
A
B
D
C
5
1
同位角
观察∠1和∠5两角:
分别在截线的左侧,在被截直线的下方
两角在截线的同一侧
两角在两条被截直线同一方
这样位置的一对角就是
5
1
7
8
5
4
1
3
2
6
2
6
7
3
8
4
图中的同位角除∠1和∠5外,还有……
在形如字母“F”的图形中有同位角。
变式图形:图中的∠1与∠2都是同位角。
探索交流
1
图中的∠1与∠2是同位角吗?
5
1
7
8
5
4
1
3
2
6
2
6
7
3
观察∠3和∠5两角:
Z
5
3
5
1
7
8
5
4
1
3
2
6
2
6
7
3
各有一边在同一直线上
5
3
观察∠3和∠5两角:
5
1
7
8
5
4
1
3
2
6
2
6
7
3
两角在直线EF的两侧
5
3
观察∠3和∠5两角:
E
F
5
1
7
8
5
4
1
3
2
6
2
6
7
3
两角在直线AB,CD之间
5
3
观察∠3和∠5两角:
A
B
C
D
一边都在截线上,两角在截线的两侧且在两条被截直线之间的一对角
内错角
5
3
观察∠3和∠5两角:
夹在两被截直线内,分别在截线两侧(交错)
7
8
5
4
1
3
2
6
5
3
4
6
图中的内错角除∠3和∠5外,还有……
图中的∠1与∠2都是内错角吗?
图形特征:在形如“Z”的图形中有内错角。
探索交流
1
图中的∠1与∠2都是内错角
5
1
7
8
5
4
1
3
2
6
观察∠3和∠6:
3
6
U
5
1
7
8
5
4
1
3
2
6
2
6
7
3
各有一边在同一直线上
3
6
观察∠3和∠6:
5
1
7
8
5
4
1
3
2
6
2
6
7
3
两角在直线EF的同一侧
3
6
观察∠3和∠6:
A
B
C
D
E
F
5
1
7
8
5
4
1
3
2
6
2
6
7
3
两角在直线AB,CD之间
3
6
观察∠3和∠6:
A
B
C
D
一边都在截线上,两角在截线的同侧且在两条被截直线之间的一对角
同旁内角
3
6
观察∠3和∠6:
在截线同旁,夹在两被截直线内
7
8
5
4
1
3
2
6
5
4
3
6
图中的同旁内角除∠3和∠6外,还有……
形如字母“U”
在两条被截直线之间,在截线同侧
同旁内角
形如字母“Z”
(或反置)
在两条被截直线之间,在截线两侧(交错)
内错角
形如字母“F”
(或倒置)
在两条被截直线同旁,在截线同侧
同位角
图形结构特征
位 置 特 征
角的名称
课堂练习
识别哪些角是同位角、内错角、同旁内角。
1
2
(1)
同位角
1
2
(2)
1
2
(3)
1
2
(4)
1
2
(5)
a
b
c
1
2
(6)
1
2
(7)
1
2
(8)
1
2
1
2
(9)
(10)
同位角
同位角
同位角
同位角
内错角
同旁内角
1、直线AB、CD相交于点O,∠1=28°
求∠2和∠3.
变式1:若∠AOC+∠BOD=100°
求∠BOC的度数.
变式2:若OM、ON分别平分∠AOD、∠BOD,求∠MON的度数.
垂直的定义的应用格式
∵∠AOC=90°(已知),
∴AB⊥CD(垂直的定义).
如果直线AB、CD 相交于点O,∠AOC=90°(或三个角中的一个角等于90°),那么 AB⊥CD.
这个推理过程可以写成:
∵AB⊥CD(已知),
∴∠AOC=90°(垂直的定义).
如果AB⊥CD,那么所得的四个角中,必有一个是直角.这个推理过程可以写成:
1、下面四种判定两条直线的垂直的方法,正确的有( )个
(1)两条直线相交所成的四个角中有一个角是直角,则这两条直线互相垂直
(2)两条直线相交,只要有一组邻补角相等,则这两条直线互相垂直
(3)两条直线相交,所成的四个角相等,这两条直线互相垂直
(4)两条直线相交,有一组对顶角互补,则这两条直线互相垂直
( A) 4 (B) 3
(C) 2 (D) 1
A
概念辨析
直线AB,CD相交于点O,OM⊥AB于O,且
DOM =∠COM,求∠AOD的度数.
垂线性质一
过一点有且只有一条直线与已知直线垂直.
线段、射线的垂线应怎么画呢?
A
B
P
Q
O
A
或作射线的反向延长线
作线段的延长线
.
.
A
O
1、如图,点A处是一座小屋,BC是一条公路,一人在O处。
(1)此人到小屋去,怎样走最近?为什么?
(2)此人要到公路去,怎样走最近?为什么?
垂线段是垂线上的一部分,它是线段,一端是一个点,另一端是垂足。
A
B
P
D
1、下列说法正确的是( )
A
B
C
D
(A)线段AB叫做点B到直线AC的距离
(B)线段AB的长度叫做点A到直线AC的距离
(C)线段BD的长度叫做点D到直线BC的距离
(D)线段BD的长度叫做点B到直线AC的距离
D
1、如图,过点P把两条笔直的公路连接起来,在图中画出最短连接的路线.
2、过一个角的顶点作这个角两边的垂线,若这两条垂线的夹角为α,求原来已知角的大小.
m
n
P
●
如图:直线a、b被直线 l 截的8个角中
同位角:
∠1与∠5 , ∠2与∠6 ,
∠3与∠7 , ∠4与∠8.
内错角:
∠3与∠5 , ∠4与∠6.
同旁内角:
∠4与∠5 , ∠3与∠6.
1
4
3
2
8
7
6
5
b
a
l
A
B
D
C
F
E
1
2
3
4
5
6
7
8
9
10
11
12
练一练
(1)∠1和 ∠9是由直线 、
被直线 所截成的 角 ;
(2)∠6和 ∠12是由直线 、
被直线 所截成的 角 ;
(3)∠4和 ∠6是由直线 、
被直线 所截成的 角 ;
(4)由直线AB、CD被直线EF所截成的同位角有 ;
(5)∠7和 ∠12是 角 ;
在判断两个角时一定要先知道由哪两条直线被哪条直线所截呦!
AB
CD
EF
同位
AB
EF
CD
内错
AB
CD
EF
同旁内
∠1 和∠9、 ∠4和 ∠12、∠2和∠10、 ∠3 和∠11
同旁内
(4).如图所示5个角中, ∠1 和∠3是______角,
∠1 和∠4是_____ 角, ∠2和∠5是_____ 角,
∠1 和∠5是______ 角, ∠3和∠4是_____ 角。
3
1
5
2
4
(3题)
(5).如图: ∠1 与∠C是直线______与直线_______被直线______所截的。 ∠2与_____是同旁内角,与∠B是同位角的有______________。
E
A
B
D
C
1
3
2
(4题)
内错
邻补
同旁内
对顶
同位
AC
BC
AD
∠B
∠3, ∠EAC
1、平行线的定义
同一平面内,不相交的两条直线叫做平行线。
(1)如果没有“同一平面内”,不相交的两条直线平行吗?
(2)定义中的“直线”能改成“线段或射线”吗?
想一想
我们通常用“//”表示平行。
2:平行线的表示法:
C
D
B
A
·
·
·
·
m ∥ n
AB ∥ CD
m
n
读作: “AB 平行于 CD”
读作: “ m平行于n ”
探究二:
同一平面内的两条不重合的直线的位置关系只有两种:
相交或平行
在同一平面内,两条直线有几
种位置关系呢?
3、平行线的画法:
一放
二靠
三移(推)
四画
·
过直线AB外一点P作直线AB的平行线,看看你能作出吗?能作出几条?
·
A
B
P
动手实践
通过画图,你发现了什么?
经过直线外一点,有且只有一条直线与这条直线平行.(平行公理)
说明:人们在长期实践中总结出来的结论叫基本事实,也称为公理,它可以作为以后推理的依据.
由以上的实践你发现了什么?
说说看
存在性
唯一性
平行公理的推论:
如果两条直线都和第三条直线平行,
那么这两条直线也互相平行
几何语言表达:
a//c , c//b(已知)
a//b(如果两条直线都和第三条直线平行,
那么这两条直线也互相平行)
c
b
a
平行线的判定
1. 两条直线被第三条直线所截,如果
同位角相等,那么两直线平行。简
单地说:同位角相等,两直线平行。
∵ ∠1=∠2(已知)
∴ a∥b(同位角相等,两直线平行)
如图:
a
b
l
2
1
内错角相等,两直线平行。
∵ ____=____(已知)
∴ ___∥___(内错角相等,两直线平行)
a
b
l
1
2
① 如图: 如果∠1=∠2,
那么a与b平行吗?
∠1
∠2
a
b
如图,直线a、b被直线c所截,若∠1+∠2=180°,则a∥b。
同旁内角互补,两直线平行。
平行线的性质1(公理)
两条平行线被第三条直线所截,
同位角相等。
简单说成:两直线平行,同位角相等。
平行线的性质2
两条平行线被第三条直线所截,
内错角相等。
简单说成:两直线平行,内错角相等。
平行线的性质3
两条平行线被第三条直线所截,
同旁内角互补
简单说成:两直线平行,同旁内角互补。
平行线的判定 平行线的性质
条件 结论 条件 结论
同位角相等 两直线平行 两直线平行 同位角相等
内错角相等 内错角相等
同旁内角互补 同旁内角互补
在同一个平面内,垂直于同一条直线的两条直线平行。
※相交※
1.直线AB、CD相交与于O,图中有几对对顶角?邻补角
当一个角确定了,另外三个角的大小确定了吗
2.直线AB、CD、EF相交与于O,图中有几对对顶角?
∠AOC的对顶角是_______
∠COF的对顶角是________
∠AOC的邻补角是______
∠EOD的邻补角是_______
3.对顶角、邻补角的性质:
O
A
B
C
D
1
2
3
4
A
B
C
D
E
F
O
∠BOD
∠DOE
∠COB, ∠AOD
∠DOF, ∠COE
对顶角相等
邻补角互补
你能量出C到AB的距离,B到AC的距离,A到BC的距离吗
A
D
C
B
E
F
理由:垂线段最短
拓 展 应 用
如图:要把水渠中的水引到水池C中,在渠岸的什么地方开沟,水沟的长度才能最短?
请画出图来,并说明理由。
C
∟
理由:垂线段最短
在平面内,两条直线有几种位置关系
什么叫平行线?怎样表示?怎样读?
平行公理及其推论的内容是什么?
有哪些方法画平行线?
两直线被第三直线所截,构成的八个角中同位角有 __对,内错角有__对,同旁内角有__对.
平行线的判定方法有哪些?
平行线有哪些性质?
什么是平行线间的距离?
∥平行∥
4
2
2
F
1
3
7
5
2
4
8
6
D
C
A
B
E
.如图, 若∠3=∠4,则 ∥ ;
AD
1
⌒
⌒
⌒
⌒
A
B
C
D
1
4
3
2
若AB∥CD, 则∠ =∠ 。
BC
2
.如图,∠D=70°,∠C= 110°,
∠1=69°,则∠B= ·
B
A
C
E
D
⌒
1
69°
⌒
⌒
⌒
⌒
A
B
C
D
1
4
3
2
3 . 如图,已知AB∥CD,补充什么条件,能得AD//BC?
综合练习
6. 已知,如图AB∥EF∥CD,AD∥BC,BD平分∠ABC,则图中与∠EOD相等的角有( )个.
A. 2
B. 3
C. 4
D. 5
A
B
C
D
E
F
O
D
7.如图,填空
(1)∵∠B=∠1(已知)
∴____//____( )
(2)∵CG // DF(已知)
∴∠2= ( )
(3)∵∠3=∠A(已知)
∴____//____( )
(4)∵AG // DF(已知)
∴∠3=_____( )
同位角相等,两直线平行
AB
DE
∠F
两直线平行,同位角相等
AB
DE
内错角相等,两直线平行
∠D
两直线平行,内错角相等
(5)∵∠B+∠4=180°(已知)
∴____//____( )
(6)∵CG // DF(已知)
∴∠F+ =180°( )
同旁内角互补,两直线平行
AB
DE
∠5
两直线平行,同旁内角互补
9、如图,已知∠AEM= ∠DGN,则你能说明AB平行于CD吗?
变式1:若∠AEM= ∠DGN,EF、GH分别平分∠AEG和∠CGN,则图中还有平行线吗?
变式2:若∠AEM= ∠DGN,∠1=∠2,则图中还有平行线吗?
练习:
⒈ 如图⑴,已知 AB∥CD, ∠1=30°, ∠2=90°,则∠3=______°
⒉ 如图⑵,若AE∥CD, ∠EBF=135°, ∠BFD=60°,∠D= ( )
A、75° B、45° C、30° D、15°
图1
图2
30°
?
135°
?
60°
1、如图,已知AB∥CD,∠ABF=∠DCE.
试说明:∠BFE=∠FEC.
?
?
ys
l
p
yx
a
d
c
b
3
1
2
2.如图,以下是某位同学
作业中的一段说理:
如果∠1=∠2 ,那么
根据同位角相等,两直线平行,
可得a∥b;
如果∠2+∠3=180 °,那么
根据两直线平行,同旁内角互补,
可得c∥d。你认为他说得对吗?
___
___
______________
若OE⊥AB ,∠1=56°,
则∠3=_____。
E
3
O
A
B
C
D
2
1
3.若∠BOC=2∠1,
则∠1=______,
∠BOC=_______。
34°
60°
120 °
4.(算算看)已知如图,OB⊥OA,直线CD过O,∠BOD=110°,
求∠AOC的度数?
∠BOD=110° ∠BOC=70° ∠AOC=20°
5.点到直线的距离是____
点到直线上一点的连线
点到直线的垂线
点到直线的垂线段
点到直线的垂线段的长度
6.如图,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.
因为EF∥AD,
所以∠2=____(______________________)
又因为∠1=∠2
所以∠1=∠3(______________)
所以AB∥_____(__________________________)
所以∠BAC+______=180°(________________)
因为∠BAC=70°
所以∠AGD=_______
1、观察右图并填空:
(1) ∠1 与 是同位角;
(2) ∠5 与 是同旁内角;
(3) ∠1 与 是内错角;
b
a
n
m
2
3
1
4
5
∠4
∠3
∠2
2、当图中各角满足下列条件时,你能指出哪两条直线平行
(1) ∠1 = ∠4;
(2) ∠2 = ∠4;
(3) ∠1 + ∠3 = 180 ;
a
b
l
m
n
1
2
3
4
基础练习:
a ∥ b
l∥m
l∥ n
3.如图:∠ 1=100°∠2=80°,
∠3=105° 则∠4=_______
a
b
c
d
1
2
3
4
4. 两条直线被第三条直线所截,则( )
A 同位角相等 B 同旁内角互补
C 内错角相等 D 以上都不对
基础练习:
105°
D
5.如图, 若∠3=∠4,则 ∥ ;
AD
1
⌒
⌒
⌒
⌒
A
B
C
D
1
4
3
2
若AB∥CD, 则∠ =∠ 。
BC
2
6.如图,∠D=70°,∠C= 110°,∠1=69°,
则∠B= ·
B
A
C
E
D
⌒
1
69°
基础练习:
B
C
E
F
D
A
一题多解:
如图,直线EF过点A, D是BA延长线上的点 ,具备什么条件时,可以判定EF∥BC 为什么
例1、 已知∠DAC= ∠ACB, ∠D+∠DFE=1800,求证:EF//BC
证明: 因为 ∠DAC= ∠ACB (已知)
所以 AD// BC
(内错角相等,两直线平行)
因为 ∠D+∠DFE=1800(已知)
所以AD// EF
(同旁内角互补,两直线平行)
因为 EF// BC
(平行于同一条直线的两条直线互相平行)
A
B
C
D
E
F
例题精讲:
例2 : 如图,BD⊥AC,EF⊥AC,D、F分别为垂足,∠1=∠2,试说明∠ADG =∠C 。
例题精讲:
解:∵ BD⊥AC,EF⊥AC(已知)
∴ BD∥EF(同时垂直于第三条直线的两条直线平行)
∴∠CBD=∠2(两直线平行,同位角相等)
∵ ∠1=∠2(已知)
∴∠CBD=∠1(等量代换)
∴BC ∥ DG(内错角相等,两直线平行)
∴ ∠ADG =∠C (两直线平行,同位角相等)
证明: 因为由AC∥DE (已知)
所以∠ACD= ∠2 (两直线平行,内错角相等)
因为∠1=∠2(已知)
所以 ∠1=∠ACD(等量代换)
所以AB ∥ CD
(内错角相等,两直线平行)
A
D
B
E
1
2
C
例题精讲:
如图,已知:AC∥DE,∠1=∠2,试证明AB∥CD.
已知:如图AB∥CD,试探究∠BED与∠B,∠D的关系
F
1
2
F
1
2
A
B
C
D
E
探究创新:
n条直线相交于一点,有 组对顶角。
n(n-1)
一个角的两边与另一个角的两边分别平行,则这两个角相等或互补。
两条直线平行,那么它们的同位角的角平分线也互相平行;内错角的角平分线也互相平行;同旁内角的角平分线互相垂直。
本章几个重要的结论:
相交线
两条
直线
相交
两条直线被
第三条所截
一般情况
邻补角
对顶角
邻补角互补
对顶角相等
特殊
垂直
存在性和唯一性
垂线段最短
点到直线的距离
同位角、内错角、同旁内角
平行线
平行公理及其推论
平行线的判定
平行线的性质
一、相交线:
A
B
C
D
O
A
B
C
D
O
7
2
4
A
B
C
D
E
F
1
3
5
6
8
垂直
斜交
三线八角
如图,直线AB与CD相交,∠1和∠2有一条公共边,它们的另一条边互为反向延长线,具有这种关系的两个角叫做互为邻补角。
互为邻补角的两个角和为180。
4
2
3
1
C
D
A
B
O
互为邻补角和互为补角有什么区别?
问题
互为邻补角
有一条公共边,它们的另一条边互为反向延长线;它们的和为180。
互为补角
它们的位置不确定;它们的和是180。
对顶角的概念
如下图所示,∠1与∠3有什么特点?
∠1和∠3具有相同的顶点,且∠1的两边OA、OC分别与∠3的两边OB、OD互为反向延长线,
4
2
3
1
C
D
A
B
O
射线OA的反向延长线是指从点A到点O方向延长得到的一条射线,即射线OB。
我们把这样的两个角叫做对顶角。∠2和∠4也是对顶角.
如图,直线AB与CD相交,∠1和∠3有公共顶点,并且它们的两边分别互为反向延长线,具有这种关系的两个角叫做互为对顶角。
4
2
3
1
C
D
A
B
O
猜想
1、对顶角在数量上有什么关系?
2、你可以用哪些方法进行验证?
O
A
B
C
D
)
(
1
3
4
2
)
(
已知:直线AB与CD相交于O点(如图),说明∠1=∠3、 ∠2=∠4的理由
解:∵直线AB与CD相交于O点,
∴∠1+∠2=180°、 ∠2+∠3=180°(邻补角的定义)
∴∠1=∠3(同角或等角的补角相等)
同理可得:∠2=∠4
对顶角相等
垂线的定义
2.垂直用符号 “⊥”来表示,读作“垂直于”。
如图“直线AB 垂直于直线CD ”,就记作“AB⊥CD ”,交点O 叫做垂足。
1.定义:当两条直线相交所成的四个角 中有一个角 是直角 时,我们就说这两条直线互相垂直。
O
A
B
C
D
“ ”是图形中“垂直”(直角)的标记
我们把其中一条直线叫做另一条直线的垂线
O
C
D
A
B
画已知直线AB的垂线
垂线的画法:
l
A
如图,已知直线 l 和l外的一点A ,作l的垂线.
B
则所画直线AB是过点A的直线l的垂线.
请同学们画一下
垂线段:线段AB
垂线的性质
P
从上面的画图过程中,你能得到什么结论?不妨说说看!
垂线的性质(1):平面内,过直线上一点或直线外一点有且只有一条直线与已知直线垂直。
A
P
B
A
B
过一点,有且只有一条直线与已知直线垂直。
线段、射线的垂线应怎么画呢?
A
B
P
Q
O
A
线段的延长线
或射线的反向延长线
A
B
C
D
O
(二)、垂直:
2、画法:
3、性质:
两条直线相交所形成的四个角中有一个是直角时叫两条直线互相垂直。
过一点画一条直线的垂线。
P
a
Q
(1)、过一点有且只有一条直线垂直于已知直线。
p
A
B
C
D
E
(2)、 垂线段最短。
点到直线的距离:
b
b
c
1、定义:
点到直线的距离: 从直线外一点到这条直线的 垂线段的长度,叫做这点到这条直线的距离.
判断:
1、画出点A到直线BC的距离。( )
2、画出点A到直线BC的垂线段。( )
3、量出点A到直线BC的距离。 ( )
4、垂线最短。 ( )
B
C
A
D
5、如图,AC⊥BC,CD ⊥AB,垂足分别是C点、D点。
(1)点B到CD的距离是线段______的长度;
(2)点C到AB的距离是线段______的长度;
(3)点A到CB的距离是线段______的长度。
A
B
C
D
BD
CD
AC
过一点画已知直线的垂线的方法
过一点画垂线的方法可归纳为“一靠、二过、三画、四标”
1.一靠:把三角板的一条直角边靠在已知直线上;
2.二过:让三角板的另一条直角边经过已知点;
A
B
P
3.三画:沿着已知点所在的直角边画直线;
∟
4.四标:标上直角符号“ ”。
P
如图,线段AB叫做点A到直线l 的垂线段,
注意他们的区别!
A
B
C
l
D
点到直线的距离:
直线外一点到直线的垂线段的长度,叫做点到直线的距离。
线段AB的长度就是点A到直线l 的距离
如图 ,已知AB. CD相交于O, OE⊥CD
于O,∠AOC=36°,则∠BOE= 。
(A)36°
(B) 64°
(C)144°
(D) 54°
A
B
O
C
D
E
54°
随堂练习
1、判断
1)一条直线的垂线只能画一条( )
2)两直线相交所构成的四个角相等,则这两直线互相垂直( )
3)点到直线的垂线段就是点到直线的距离( )
4)在同一平面内,过一点有且只有一条直线与已知直线垂直( )
×
√
×
√
3、如图:在铁路旁边有一张庄,现在要建一火车站,为了使张庄人乘火车最方便(即距离最近),请你在铁路上选一点来建火车站,并说明理由。
张庄
∟
P
小试牛刀
1、直线m外有点P,它到直线m上点A、B、C的距离分别是6厘米、3厘米、5厘米,则点P到直线m的距离( )
A等于6厘米. B.等于3厘米 C.等于5厘米 D.不大于3厘米
2、如右图,若OC⊥AB于点O,OE⊥OD,
则图中互余的角有( )
A. 4对 B. 3对 C. 2对 D. 1对
A
B
O
D
C
E
3、如右图,直线a、b、c相交于一点,若∠1 :∠2 :∠3=1 : 2 : 3,则∠2的度数为____度。 ∠3的度数为 _______度。直线a、b的位置关系是____________。
1
2
3
a
b
c
D
A
60
90
互相垂直
4、如右图,按要求完成下列各题:
m
A
B
⑴请画出由A地经过B地去河边m的最短路线;
⑵确定A地去B地的路线的依据是:___________________;
⑶确定B地去河边的路线的依据是:______________。
5、如图,直线AB和CD相交于点O,
OB平分∠DOF,
OE⊥AB,O为垂足,∠1=50°,
求∠AOC和∠COF的度数。
A
B
D
E
O
1
C
F
能力挑战:
C
两点之间,线段最短
垂线段最短
中考在线:【2008·四川乐山】
如图,直线l1与l2相交于点O,OM⊥l1,
若α=44°,则β=( )
l1
l2
O
M
α
β
46°
练习
一、下列叙述中不正确的是( )
(A)经过直外一点只能画一条已知道直线的垂线
(B)如果两条直线相交所构成的四个角中有三个角度相等,那么这两条直线一定垂直
(C)直线l上有三点A、B、C,在直线l个外有一点P,若PB
C
二、一辆汽车在直线型公路AB 上由A向B行驶,M、N分别是位于公路两侧的村庄,设汽车行驶到P位置时离村庄M最近;行驶到Q位置时离村庄N最近,请在图中公路AB上分别画出P、Q两点的位置
A
B
M
N
·
·
∟
∟
P
Q
三、如图,直线AB与CD相交于点O,OE⊥CD, OF⊥AB,∠DOF=65o,求∠BOE和∠AOC的度数。
A
B
O
F
C
D
E
∵OE⊥CD, OF⊥AB (已知)
解:
∴ ∠BOF=∠DOE=90o(垂直的定义)
∴∠BOD=∠BOF-∠DOF
=90o-65o=25o
∴∠BOE=∠DOE-∠BOD=90o-25o=65o
而∠AOC=∠BOD=25o
(对顶角相等)
答: ∠BOE=65o,∠AOC=25o
A
B
C
D
E
F
1
2
3
4
5
6
7
8
同位角:
内错角:
同旁内角:
∠1与∠5; ∠4与∠8;
∠2与∠6; ∠3与∠7.
∠4与∠6; ∠3与∠5.
∠4与∠5; ∠3与∠6.
A
B
C
D
E
O
如图: ∠ A和哪个角是同位角
∠ A和哪个角是 内错角
∠ A和哪个角是同旁内角
(∠COE、 ∠COB)
(∠C、 ∠AOD)
(∠B 、 ∠AOB、 ∠AOE)
(三)、三线八角:
概念辨析
一、判断题
1、有公共顶点且相等的两个角是对顶角。( )
2、两条直线相交,有两组对顶角。 ( )
3、两条直线相交所构成的四个角中有一个角是直角,
那么其余的三个角也是直角。 ( )
二、选择题
1、如右图直线AB、CD交于点O,OE为射线,那么( )
A。∠AOC和∠BOE是对顶角;
B。∠COE和∠AOD是对顶角;
C。∠BOC和∠AOD是对顶角;
D。∠AOE和∠DOE是对顶角。
2、如右图中直线AB、CD交于O,
OE是∠BOC的平分线且∠BOE=50度,
那么∠AOE=( )度
(A)80;(B)100;(C)130(D)150。
A
B
C
D
O
E
×
√
√
C
C
A
C
B
D
E
F
如图:怎样描述这三条直线的位置关系?
直线AB、CD被EF所截
7
1
2
3
4
5
6
8
观察
截线
被截直线
观察
F
问题:1、观察∠1与∠5的位置关系
A
C
B
D
E
1
2
3
4
5
6
7
8
1
5
5
1
7
8
5
4
1
3
2
6
2
6
7
3
观察∠1和∠5两角:
F
5
1
7
8
5
4
1
3
2
6
2
6
7
3
5
1
各有一边在同一直线上
观察∠1和∠5两角:
5
1
7
8
5
4
1
3
2
6
2
6
7
3
两角在直线EF的同一侧
5
1
观察∠1和∠5两角:
E
F
5
1
7
8
5
4
1
3
2
6
2
6
7
3
两角分别在直线AB,CD同一方
5
1
观察∠1和∠5两角:
A
B
D
C
5
1
同位角
观察∠1和∠5两角:
分别在截线的左侧,在被截直线的下方
两角在截线的同一侧
两角在两条被截直线同一方
这样位置的一对角就是
5
1
7
8
5
4
1
3
2
6
2
6
7
3
8
4
图中的同位角除∠1和∠5外,还有……
在形如字母“F”的图形中有同位角。
变式图形:图中的∠1与∠2都是同位角。
探索交流
1
图中的∠1与∠2是同位角吗?
5
1
7
8
5
4
1
3
2
6
2
6
7
3
观察∠3和∠5两角:
Z
5
3
5
1
7
8
5
4
1
3
2
6
2
6
7
3
各有一边在同一直线上
5
3
观察∠3和∠5两角:
5
1
7
8
5
4
1
3
2
6
2
6
7
3
两角在直线EF的两侧
5
3
观察∠3和∠5两角:
E
F
5
1
7
8
5
4
1
3
2
6
2
6
7
3
两角在直线AB,CD之间
5
3
观察∠3和∠5两角:
A
B
C
D
一边都在截线上,两角在截线的两侧且在两条被截直线之间的一对角
内错角
5
3
观察∠3和∠5两角:
夹在两被截直线内,分别在截线两侧(交错)
7
8
5
4
1
3
2
6
5
3
4
6
图中的内错角除∠3和∠5外,还有……
图中的∠1与∠2都是内错角吗?
图形特征:在形如“Z”的图形中有内错角。
探索交流
1
图中的∠1与∠2都是内错角
5
1
7
8
5
4
1
3
2
6
观察∠3和∠6:
3
6
U
5
1
7
8
5
4
1
3
2
6
2
6
7
3
各有一边在同一直线上
3
6
观察∠3和∠6:
5
1
7
8
5
4
1
3
2
6
2
6
7
3
两角在直线EF的同一侧
3
6
观察∠3和∠6:
A
B
C
D
E
F
5
1
7
8
5
4
1
3
2
6
2
6
7
3
两角在直线AB,CD之间
3
6
观察∠3和∠6:
A
B
C
D
一边都在截线上,两角在截线的同侧且在两条被截直线之间的一对角
同旁内角
3
6
观察∠3和∠6:
在截线同旁,夹在两被截直线内
7
8
5
4
1
3
2
6
5
4
3
6
图中的同旁内角除∠3和∠6外,还有……
形如字母“U”
在两条被截直线之间,在截线同侧
同旁内角
形如字母“Z”
(或反置)
在两条被截直线之间,在截线两侧(交错)
内错角
形如字母“F”
(或倒置)
在两条被截直线同旁,在截线同侧
同位角
图形结构特征
位 置 特 征
角的名称
课堂练习
识别哪些角是同位角、内错角、同旁内角。
1
2
(1)
同位角
1
2
(2)
1
2
(3)
1
2
(4)
1
2
(5)
a
b
c
1
2
(6)
1
2
(7)
1
2
(8)
1
2
1
2
(9)
(10)
同位角
同位角
同位角
同位角
内错角
同旁内角
1、直线AB、CD相交于点O,∠1=28°
求∠2和∠3.
变式1:若∠AOC+∠BOD=100°
求∠BOC的度数.
变式2:若OM、ON分别平分∠AOD、∠BOD,求∠MON的度数.
垂直的定义的应用格式
∵∠AOC=90°(已知),
∴AB⊥CD(垂直的定义).
如果直线AB、CD 相交于点O,∠AOC=90°(或三个角中的一个角等于90°),那么 AB⊥CD.
这个推理过程可以写成:
∵AB⊥CD(已知),
∴∠AOC=90°(垂直的定义).
如果AB⊥CD,那么所得的四个角中,必有一个是直角.这个推理过程可以写成:
1、下面四种判定两条直线的垂直的方法,正确的有( )个
(1)两条直线相交所成的四个角中有一个角是直角,则这两条直线互相垂直
(2)两条直线相交,只要有一组邻补角相等,则这两条直线互相垂直
(3)两条直线相交,所成的四个角相等,这两条直线互相垂直
(4)两条直线相交,有一组对顶角互补,则这两条直线互相垂直
( A) 4 (B) 3
(C) 2 (D) 1
A
概念辨析
直线AB,CD相交于点O,OM⊥AB于O,且
DOM =∠COM,求∠AOD的度数.
垂线性质一
过一点有且只有一条直线与已知直线垂直.
线段、射线的垂线应怎么画呢?
A
B
P
Q
O
A
或作射线的反向延长线
作线段的延长线
.
.
A
O
1、如图,点A处是一座小屋,BC是一条公路,一人在O处。
(1)此人到小屋去,怎样走最近?为什么?
(2)此人要到公路去,怎样走最近?为什么?
垂线段是垂线上的一部分,它是线段,一端是一个点,另一端是垂足。
A
B
P
D
1、下列说法正确的是( )
A
B
C
D
(A)线段AB叫做点B到直线AC的距离
(B)线段AB的长度叫做点A到直线AC的距离
(C)线段BD的长度叫做点D到直线BC的距离
(D)线段BD的长度叫做点B到直线AC的距离
D
1、如图,过点P把两条笔直的公路连接起来,在图中画出最短连接的路线.
2、过一个角的顶点作这个角两边的垂线,若这两条垂线的夹角为α,求原来已知角的大小.
m
n
P
●
如图:直线a、b被直线 l 截的8个角中
同位角:
∠1与∠5 , ∠2与∠6 ,
∠3与∠7 , ∠4与∠8.
内错角:
∠3与∠5 , ∠4与∠6.
同旁内角:
∠4与∠5 , ∠3与∠6.
1
4
3
2
8
7
6
5
b
a
l
A
B
D
C
F
E
1
2
3
4
5
6
7
8
9
10
11
12
练一练
(1)∠1和 ∠9是由直线 、
被直线 所截成的 角 ;
(2)∠6和 ∠12是由直线 、
被直线 所截成的 角 ;
(3)∠4和 ∠6是由直线 、
被直线 所截成的 角 ;
(4)由直线AB、CD被直线EF所截成的同位角有 ;
(5)∠7和 ∠12是 角 ;
在判断两个角时一定要先知道由哪两条直线被哪条直线所截呦!
AB
CD
EF
同位
AB
EF
CD
内错
AB
CD
EF
同旁内
∠1 和∠9、 ∠4和 ∠12、∠2和∠10、 ∠3 和∠11
同旁内
(4).如图所示5个角中, ∠1 和∠3是______角,
∠1 和∠4是_____ 角, ∠2和∠5是_____ 角,
∠1 和∠5是______ 角, ∠3和∠4是_____ 角。
3
1
5
2
4
(3题)
(5).如图: ∠1 与∠C是直线______与直线_______被直线______所截的。 ∠2与_____是同旁内角,与∠B是同位角的有______________。
E
A
B
D
C
1
3
2
(4题)
内错
邻补
同旁内
对顶
同位
AC
BC
AD
∠B
∠3, ∠EAC
1、平行线的定义
同一平面内,不相交的两条直线叫做平行线。
(1)如果没有“同一平面内”,不相交的两条直线平行吗?
(2)定义中的“直线”能改成“线段或射线”吗?
想一想
我们通常用“//”表示平行。
2:平行线的表示法:
C
D
B
A
·
·
·
·
m ∥ n
AB ∥ CD
m
n
读作: “AB 平行于 CD”
读作: “ m平行于n ”
探究二:
同一平面内的两条不重合的直线的位置关系只有两种:
相交或平行
在同一平面内,两条直线有几
种位置关系呢?
3、平行线的画法:
一放
二靠
三移(推)
四画
·
过直线AB外一点P作直线AB的平行线,看看你能作出吗?能作出几条?
·
A
B
P
动手实践
通过画图,你发现了什么?
经过直线外一点,有且只有一条直线与这条直线平行.(平行公理)
说明:人们在长期实践中总结出来的结论叫基本事实,也称为公理,它可以作为以后推理的依据.
由以上的实践你发现了什么?
说说看
存在性
唯一性
平行公理的推论:
如果两条直线都和第三条直线平行,
那么这两条直线也互相平行
几何语言表达:
a//c , c//b(已知)
a//b(如果两条直线都和第三条直线平行,
那么这两条直线也互相平行)
c
b
a
平行线的判定
1. 两条直线被第三条直线所截,如果
同位角相等,那么两直线平行。简
单地说:同位角相等,两直线平行。
∵ ∠1=∠2(已知)
∴ a∥b(同位角相等,两直线平行)
如图:
a
b
l
2
1
内错角相等,两直线平行。
∵ ____=____(已知)
∴ ___∥___(内错角相等,两直线平行)
a
b
l
1
2
① 如图: 如果∠1=∠2,
那么a与b平行吗?
∠1
∠2
a
b
如图,直线a、b被直线c所截,若∠1+∠2=180°,则a∥b。
同旁内角互补,两直线平行。
平行线的性质1(公理)
两条平行线被第三条直线所截,
同位角相等。
简单说成:两直线平行,同位角相等。
平行线的性质2
两条平行线被第三条直线所截,
内错角相等。
简单说成:两直线平行,内错角相等。
平行线的性质3
两条平行线被第三条直线所截,
同旁内角互补
简单说成:两直线平行,同旁内角互补。
平行线的判定 平行线的性质
条件 结论 条件 结论
同位角相等 两直线平行 两直线平行 同位角相等
内错角相等 内错角相等
同旁内角互补 同旁内角互补
在同一个平面内,垂直于同一条直线的两条直线平行。
※相交※
1.直线AB、CD相交与于O,图中有几对对顶角?邻补角
当一个角确定了,另外三个角的大小确定了吗
2.直线AB、CD、EF相交与于O,图中有几对对顶角?
∠AOC的对顶角是_______
∠COF的对顶角是________
∠AOC的邻补角是______
∠EOD的邻补角是_______
3.对顶角、邻补角的性质:
O
A
B
C
D
1
2
3
4
A
B
C
D
E
F
O
∠BOD
∠DOE
∠COB, ∠AOD
∠DOF, ∠COE
对顶角相等
邻补角互补
你能量出C到AB的距离,B到AC的距离,A到BC的距离吗
A
D
C
B
E
F
理由:垂线段最短
拓 展 应 用
如图:要把水渠中的水引到水池C中,在渠岸的什么地方开沟,水沟的长度才能最短?
请画出图来,并说明理由。
C
∟
理由:垂线段最短
在平面内,两条直线有几种位置关系
什么叫平行线?怎样表示?怎样读?
平行公理及其推论的内容是什么?
有哪些方法画平行线?
两直线被第三直线所截,构成的八个角中同位角有 __对,内错角有__对,同旁内角有__对.
平行线的判定方法有哪些?
平行线有哪些性质?
什么是平行线间的距离?
∥平行∥
4
2
2
F
1
3
7
5
2
4
8
6
D
C
A
B
E
.如图, 若∠3=∠4,则 ∥ ;
AD
1
⌒
⌒
⌒
⌒
A
B
C
D
1
4
3
2
若AB∥CD, 则∠ =∠ 。
BC
2
.如图,∠D=70°,∠C= 110°,
∠1=69°,则∠B= ·
B
A
C
E
D
⌒
1
69°
⌒
⌒
⌒
⌒
A
B
C
D
1
4
3
2
3 . 如图,已知AB∥CD,补充什么条件,能得AD//BC?
综合练习
6. 已知,如图AB∥EF∥CD,AD∥BC,BD平分∠ABC,则图中与∠EOD相等的角有( )个.
A. 2
B. 3
C. 4
D. 5
A
B
C
D
E
F
O
D
7.如图,填空
(1)∵∠B=∠1(已知)
∴____//____( )
(2)∵CG // DF(已知)
∴∠2= ( )
(3)∵∠3=∠A(已知)
∴____//____( )
(4)∵AG // DF(已知)
∴∠3=_____( )
同位角相等,两直线平行
AB
DE
∠F
两直线平行,同位角相等
AB
DE
内错角相等,两直线平行
∠D
两直线平行,内错角相等
(5)∵∠B+∠4=180°(已知)
∴____//____( )
(6)∵CG // DF(已知)
∴∠F+ =180°( )
同旁内角互补,两直线平行
AB
DE
∠5
两直线平行,同旁内角互补
9、如图,已知∠AEM= ∠DGN,则你能说明AB平行于CD吗?
变式1:若∠AEM= ∠DGN,EF、GH分别平分∠AEG和∠CGN,则图中还有平行线吗?
变式2:若∠AEM= ∠DGN,∠1=∠2,则图中还有平行线吗?
练习:
⒈ 如图⑴,已知 AB∥CD, ∠1=30°, ∠2=90°,则∠3=______°
⒉ 如图⑵,若AE∥CD, ∠EBF=135°, ∠BFD=60°,∠D= ( )
A、75° B、45° C、30° D、15°
图1
图2
30°
?
135°
?
60°
1、如图,已知AB∥CD,∠ABF=∠DCE.
试说明:∠BFE=∠FEC.
?
?
ys
l
p
yx
a
d
c
b
3
1
2
2.如图,以下是某位同学
作业中的一段说理:
如果∠1=∠2 ,那么
根据同位角相等,两直线平行,
可得a∥b;
如果∠2+∠3=180 °,那么
根据两直线平行,同旁内角互补,
可得c∥d。你认为他说得对吗?
___
___
______________
若OE⊥AB ,∠1=56°,
则∠3=_____。
E
3
O
A
B
C
D
2
1
3.若∠BOC=2∠1,
则∠1=______,
∠BOC=_______。
34°
60°
120 °
4.(算算看)已知如图,OB⊥OA,直线CD过O,∠BOD=110°,
求∠AOC的度数?
∠BOD=110° ∠BOC=70° ∠AOC=20°
5.点到直线的距离是____
点到直线上一点的连线
点到直线的垂线
点到直线的垂线段
点到直线的垂线段的长度
6.如图,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.
因为EF∥AD,
所以∠2=____(______________________)
又因为∠1=∠2
所以∠1=∠3(______________)
所以AB∥_____(__________________________)
所以∠BAC+______=180°(________________)
因为∠BAC=70°
所以∠AGD=_______
1、观察右图并填空:
(1) ∠1 与 是同位角;
(2) ∠5 与 是同旁内角;
(3) ∠1 与 是内错角;
b
a
n
m
2
3
1
4
5
∠4
∠3
∠2
2、当图中各角满足下列条件时,你能指出哪两条直线平行
(1) ∠1 = ∠4;
(2) ∠2 = ∠4;
(3) ∠1 + ∠3 = 180 ;
a
b
l
m
n
1
2
3
4
基础练习:
a ∥ b
l∥m
l∥ n
3.如图:∠ 1=100°∠2=80°,
∠3=105° 则∠4=_______
a
b
c
d
1
2
3
4
4. 两条直线被第三条直线所截,则( )
A 同位角相等 B 同旁内角互补
C 内错角相等 D 以上都不对
基础练习:
105°
D
5.如图, 若∠3=∠4,则 ∥ ;
AD
1
⌒
⌒
⌒
⌒
A
B
C
D
1
4
3
2
若AB∥CD, 则∠ =∠ 。
BC
2
6.如图,∠D=70°,∠C= 110°,∠1=69°,
则∠B= ·
B
A
C
E
D
⌒
1
69°
基础练习:
B
C
E
F
D
A
一题多解:
如图,直线EF过点A, D是BA延长线上的点 ,具备什么条件时,可以判定EF∥BC 为什么
例1、 已知∠DAC= ∠ACB, ∠D+∠DFE=1800,求证:EF//BC
证明: 因为 ∠DAC= ∠ACB (已知)
所以 AD// BC
(内错角相等,两直线平行)
因为 ∠D+∠DFE=1800(已知)
所以AD// EF
(同旁内角互补,两直线平行)
因为 EF// BC
(平行于同一条直线的两条直线互相平行)
A
B
C
D
E
F
例题精讲:
例2 : 如图,BD⊥AC,EF⊥AC,D、F分别为垂足,∠1=∠2,试说明∠ADG =∠C 。
例题精讲:
解:∵ BD⊥AC,EF⊥AC(已知)
∴ BD∥EF(同时垂直于第三条直线的两条直线平行)
∴∠CBD=∠2(两直线平行,同位角相等)
∵ ∠1=∠2(已知)
∴∠CBD=∠1(等量代换)
∴BC ∥ DG(内错角相等,两直线平行)
∴ ∠ADG =∠C (两直线平行,同位角相等)
证明: 因为由AC∥DE (已知)
所以∠ACD= ∠2 (两直线平行,内错角相等)
因为∠1=∠2(已知)
所以 ∠1=∠ACD(等量代换)
所以AB ∥ CD
(内错角相等,两直线平行)
A
D
B
E
1
2
C
例题精讲:
如图,已知:AC∥DE,∠1=∠2,试证明AB∥CD.
已知:如图AB∥CD,试探究∠BED与∠B,∠D的关系
F
1
2
F
1
2
A
B
C
D
E
探究创新:
n条直线相交于一点,有 组对顶角。
n(n-1)
一个角的两边与另一个角的两边分别平行,则这两个角相等或互补。
两条直线平行,那么它们的同位角的角平分线也互相平行;内错角的角平分线也互相平行;同旁内角的角平分线互相垂直。
本章几个重要的结论:
