辽宁省2021-2022学年高二上学期合格考数学模拟试题word版含答案
文档属性
| 名称 | 辽宁省2021-2022学年高二上学期合格考数学模拟试题word版含答案 |  | |
| 格式 | doc | ||
| 文件大小 | 372.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-31 07:56:27 | ||
图片预览


文档简介
辽宁省普通高中学业水平合格性考试模拟试卷
数 学
(本试卷分Ⅰ、Ⅱ两卷,满分100分,考试时间90分钟,命题人:刘海刚)
第Ⅰ卷(选择题 共36分)
1、选择题:本大题共12小题,每小题3分,共36分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A={1,2,3},B={3,4,5},则A∪B=( ).
A.{1,2} B.{3} C.{1,2,4,5} D.{1,2,3,4,5}
2.计算的模为( ).
A.1+i B.-1+i C.2 D.
3.如果命题,则为( ).
A. B.
C. D.
4.如图,梯形ABCD,AECD,BFCD,则等于( ).
A. B.
C. D.
5.如果一个长方体长、宽、高分别是3,4,5,则它的体积为( )。
A.60 B.30 C. 20 D. 94
6.不等式的解集为( )。
A.(-1,3) B. C. (-3,1) D.
7.已知向量,,则( ).
A.0 B.-3 C.-4 D. 4
8.函数的定义域为( ).
A. B. C. D.
9. 如图所示是一个容量为100的样本频率分布直方图,则由图中的数据可知,样本落在[15,20]内的频数为( )。
A. 20 B.30
C. 40 D. 50
10.函数的最小正周期为( )。
A. B. C. D.
11.已知,则是下列不等式一定成立的是( )。
A. B. C. D.
12.已知函数。若函数有四个零点,则的值为( )。
A. B.3 C. D.6
答题卡 题号 1 2 3 4 5 6 7 8 9 10 11 12
答案
二、填空题:本大题共4小题,每小题3分,共12分。要求直接写出答案,不必写出计算过程或推理过程。
13.计算的值为 。
14.已知一组数的平均数为3,则另一组数的平均数为 。
15.已知是锐角,且,则的值为 。
16.已知,则函数的最小值为 。
三、解答题:本大题共5小题,共52分。解答题写出文字说明、证明或演算步骤。
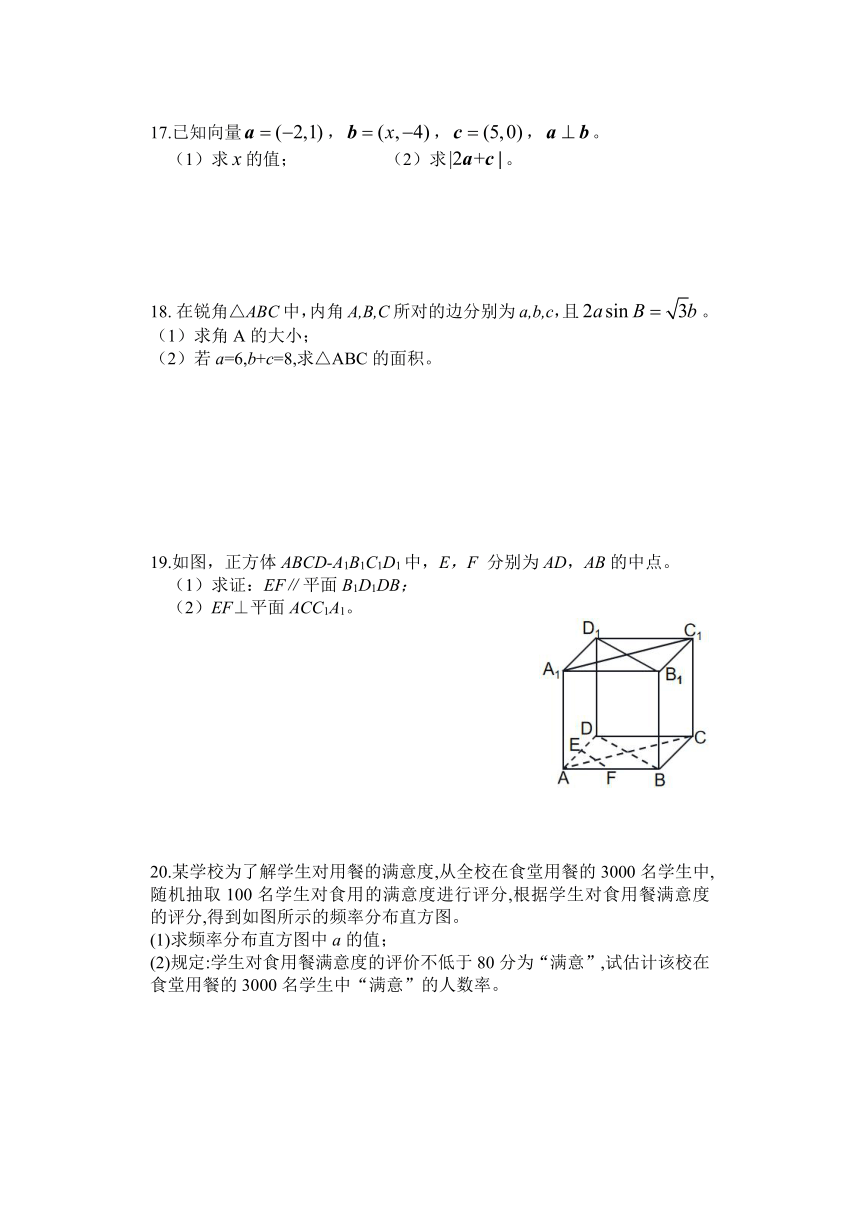
17.已知向量,,,。
(1)求的值; (2)求。
18. 在锐角△ABC中,内角A,B,C所对的边分别为a,b,c,且。
(1)求角A的大小;
(2)若a=6,b+c=8,求△ABC的面积。
19.如图,正方体ABCD-A1B1C1D1中,E,F 分别为AD,AB的中点。
(1)求证:EF∥平面B1D1DB;
(2)EF⊥平面ACC1A1。
20.某学校为了解学生对用餐的满意度,从全校在食堂用餐的3000名学生中,随机抽取100名学生对食用的满意度进行评分,根据学生对食用餐满意度的评分,得到如图所示的频率分布直方图。
(1)求频率分布直方图中a的值;
(2)规定:学生对食用餐满意度的评价不低于80分为“满意”,试估计该校在食堂用餐的3000名学生中“满意”的人数率。
21.已知定义在R上的函数。
(1)求的值;
(2)判断函数的奇偶性;
(3)若方程的两根为与,求的值。
辽宁省普通高中学业水平合格性考试模拟试卷
数 学 答 案
一、选择题:
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 D D C A A B A B B D A D
二、填空题:
13. 1 14. 7 15. 16. 4
三、解答题:
17.已知向量,,,。
(1)求的值; (2)求。
解:(Ⅰ)因为,,,所以……………3分
解得………………………………………………………………………2分
(Ⅱ)因为,,所以………2分
所以………………………………………………………3分
18.在锐角△ABC中,内角A,B,C所对的边分别为a,b,c,且。
(1)求角A的大小;
(2)若a=6,b+c=8,求△ABC的面积。
解:(1)设,则,…………………………2分
因为,所以,
即……………………………………………………2分
因为,所以,
因为△ABC 为锐角三角形,所以………………………………………2分
(2)因为,所以
…………………………………………………………………2分
因为a=6,b+c=8,所以
解得……………………………………………………………………2分
……………………………………2分
19.如图,正方体ABCD-A1B1C1D1中,E,F 分别为AD,AB的中点。
(1)求证:EF∥平面B1D1DB;
(2)EF⊥平面ACC1A1。
证明:(1)因为E,F 分别为AD,AB的中点,
所以EF为 ABD的中位线。
所以……………………………2分
因为,
,
EF∥平面B1D1DB…………………………3分
(2)因为正方体ABCD-A1B1C1D1中,四边形ABCD为正方形,所以BD⊥AC
………………………………………………………………………………1分
因为,所以EF⊥AC……………………………………………1分
A1A⊥平面ABCD,,所以A1A⊥EF………………1分
因为,,,
所以EF⊥平面ACC1A1……………………………………………………2分
20.某学校为了解学生对用餐的满意度,从全校在食堂用餐的3000名学生中,随机抽取100名学生对食用的满意度进行评分,根据学生对食用餐满意度的评分,得到如图所示的频率分布直方图。
(1)求频率分布直方图中a的值;
(2)规定:学生对食用餐满意度的评价不低于80分为“满意”,试估计该校在食堂用餐的3000名学生中“满意”的人数。
解:(1)设第四组高度为a,则
…………………………………………………3分
解得…………………………………2分
(2)后两组的频率为
…………………3分
所以该校在食堂用餐的3000名学生中“满意”的人数为2100……………………2分
21.已知定义在R上的函数。
(1)求的值;
(2)判断函数的奇偶性;
(3)若方程的两根为与,求的值。
解:(1)因为定义在R上的函数 ,所以。
…………………………………………………………………………………4分
(2)因为定义域为R,满足任意,则。对于任意实数x,
.所以函数为偶函数。
…………………………………………………………………………………4分
(3),即。整理得。两根为与,则
,………………………………………………………2分
………………………………2分
数 学
(本试卷分Ⅰ、Ⅱ两卷,满分100分,考试时间90分钟,命题人:刘海刚)
第Ⅰ卷(选择题 共36分)
1、选择题:本大题共12小题,每小题3分,共36分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A={1,2,3},B={3,4,5},则A∪B=( ).
A.{1,2} B.{3} C.{1,2,4,5} D.{1,2,3,4,5}
2.计算的模为( ).
A.1+i B.-1+i C.2 D.
3.如果命题,则为( ).
A. B.
C. D.
4.如图,梯形ABCD,AECD,BFCD,则等于( ).
A. B.
C. D.
5.如果一个长方体长、宽、高分别是3,4,5,则它的体积为( )。
A.60 B.30 C. 20 D. 94
6.不等式的解集为( )。
A.(-1,3) B. C. (-3,1) D.
7.已知向量,,则( ).
A.0 B.-3 C.-4 D. 4
8.函数的定义域为( ).
A. B. C. D.
9. 如图所示是一个容量为100的样本频率分布直方图,则由图中的数据可知,样本落在[15,20]内的频数为( )。
A. 20 B.30
C. 40 D. 50
10.函数的最小正周期为( )。
A. B. C. D.
11.已知,则是下列不等式一定成立的是( )。
A. B. C. D.
12.已知函数。若函数有四个零点,则的值为( )。
A. B.3 C. D.6
答题卡 题号 1 2 3 4 5 6 7 8 9 10 11 12
答案
二、填空题:本大题共4小题,每小题3分,共12分。要求直接写出答案,不必写出计算过程或推理过程。
13.计算的值为 。
14.已知一组数的平均数为3,则另一组数的平均数为 。
15.已知是锐角,且,则的值为 。
16.已知,则函数的最小值为 。
三、解答题:本大题共5小题,共52分。解答题写出文字说明、证明或演算步骤。
17.已知向量,,,。
(1)求的值; (2)求。
18. 在锐角△ABC中,内角A,B,C所对的边分别为a,b,c,且。
(1)求角A的大小;
(2)若a=6,b+c=8,求△ABC的面积。
19.如图,正方体ABCD-A1B1C1D1中,E,F 分别为AD,AB的中点。
(1)求证:EF∥平面B1D1DB;
(2)EF⊥平面ACC1A1。
20.某学校为了解学生对用餐的满意度,从全校在食堂用餐的3000名学生中,随机抽取100名学生对食用的满意度进行评分,根据学生对食用餐满意度的评分,得到如图所示的频率分布直方图。
(1)求频率分布直方图中a的值;
(2)规定:学生对食用餐满意度的评价不低于80分为“满意”,试估计该校在食堂用餐的3000名学生中“满意”的人数率。
21.已知定义在R上的函数。
(1)求的值;
(2)判断函数的奇偶性;
(3)若方程的两根为与,求的值。
辽宁省普通高中学业水平合格性考试模拟试卷
数 学 答 案
一、选择题:
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 D D C A A B A B B D A D
二、填空题:
13. 1 14. 7 15. 16. 4
三、解答题:
17.已知向量,,,。
(1)求的值; (2)求。
解:(Ⅰ)因为,,,所以……………3分
解得………………………………………………………………………2分
(Ⅱ)因为,,所以………2分
所以………………………………………………………3分
18.在锐角△ABC中,内角A,B,C所对的边分别为a,b,c,且。
(1)求角A的大小;
(2)若a=6,b+c=8,求△ABC的面积。
解:(1)设,则,…………………………2分
因为,所以,
即……………………………………………………2分
因为,所以,
因为△ABC 为锐角三角形,所以………………………………………2分
(2)因为,所以
…………………………………………………………………2分
因为a=6,b+c=8,所以
解得……………………………………………………………………2分
……………………………………2分
19.如图,正方体ABCD-A1B1C1D1中,E,F 分别为AD,AB的中点。
(1)求证:EF∥平面B1D1DB;
(2)EF⊥平面ACC1A1。
证明:(1)因为E,F 分别为AD,AB的中点,
所以EF为 ABD的中位线。
所以……………………………2分
因为,
,
EF∥平面B1D1DB…………………………3分
(2)因为正方体ABCD-A1B1C1D1中,四边形ABCD为正方形,所以BD⊥AC
………………………………………………………………………………1分
因为,所以EF⊥AC……………………………………………1分
A1A⊥平面ABCD,,所以A1A⊥EF………………1分
因为,,,
所以EF⊥平面ACC1A1……………………………………………………2分
20.某学校为了解学生对用餐的满意度,从全校在食堂用餐的3000名学生中,随机抽取100名学生对食用的满意度进行评分,根据学生对食用餐满意度的评分,得到如图所示的频率分布直方图。
(1)求频率分布直方图中a的值;
(2)规定:学生对食用餐满意度的评价不低于80分为“满意”,试估计该校在食堂用餐的3000名学生中“满意”的人数。
解:(1)设第四组高度为a,则
…………………………………………………3分
解得…………………………………2分
(2)后两组的频率为
…………………3分
所以该校在食堂用餐的3000名学生中“满意”的人数为2100……………………2分
21.已知定义在R上的函数。
(1)求的值;
(2)判断函数的奇偶性;
(3)若方程的两根为与,求的值。
解:(1)因为定义在R上的函数 ,所以。
…………………………………………………………………………………4分
(2)因为定义域为R,满足任意,则。对于任意实数x,
.所以函数为偶函数。
…………………………………………………………………………………4分
(3),即。整理得。两根为与,则
,………………………………………………………2分
………………………………2分
同课章节目录
