人教课标版高中数学必修1《集合间的基本关系》课件(共18张PPT)
文档属性
| 名称 | 人教课标版高中数学必修1《集合间的基本关系》课件(共18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-31 11:24:49 | ||
图片预览






文档简介
(共18张PPT)
名 师 课 件
集合间的基本关系
知识回顾
问题探究
课堂小结
随堂检测
检测下预习效果:
点击“随堂训练”
选择“《集合间的基本关系》预习自测”
一般地,我们把研究对象统称为元素,把一些元素组成的总体叫做集合.只要构成两个集合的元素是一样的,我们就称这两个集合是相等的.
如果a是集合A中的元素,就说a属于集合A,记作a∈A;如果a不是集合A中的元素,就说a不属于集合A,记作a A.
除了用自然语言表示集合,还能用列举法、描述法表示集合.
知识回顾
问题探究
课堂小结
随堂检测
探究一:回顾旧知,提出新问
●活动① 回顾旧知
问题:元素与集合之间的关系应如何表示?(可举例进行说明)
元素与集合间是“∈”或“ ”的关系,如1∈{1,2,3};0 {1,2,3}等.
●活动② 创设情境,提出问题
对两个数a、b,应有a>b或a知识回顾
问题探究
课堂小结
随堂检测
探究二:探究集合间的关系、集合的子集以及集合的性质★▲
●活动① 归纳提炼子集的概念
观察下面4个例子,指出给定两个集合中的元素有什么关系?每个例子中的两个集合又有什么关系呢?
(1)A={1,2,3},B={1,2,3,4,5,6};
(2)C={新华中学高一(2)班全体女生},
D={新华中学高一(2)班全体学生};
(3)E={x︱x是等边三角形},F={x︱x是三角形};
(4)G={x︱x>2},H={x︱2x-1≥3}.
我们可以看到,(1)中的集合A中的任何元素都是集合B的元素,(2)中的集合C中的元素都是集合D中的元素,(3)中的集合E的任何元素都是集合F的元素,(4)中的集合G中的任何元素都是集合H中的元素.
知识回顾
问题探究
课堂小结
随堂检测
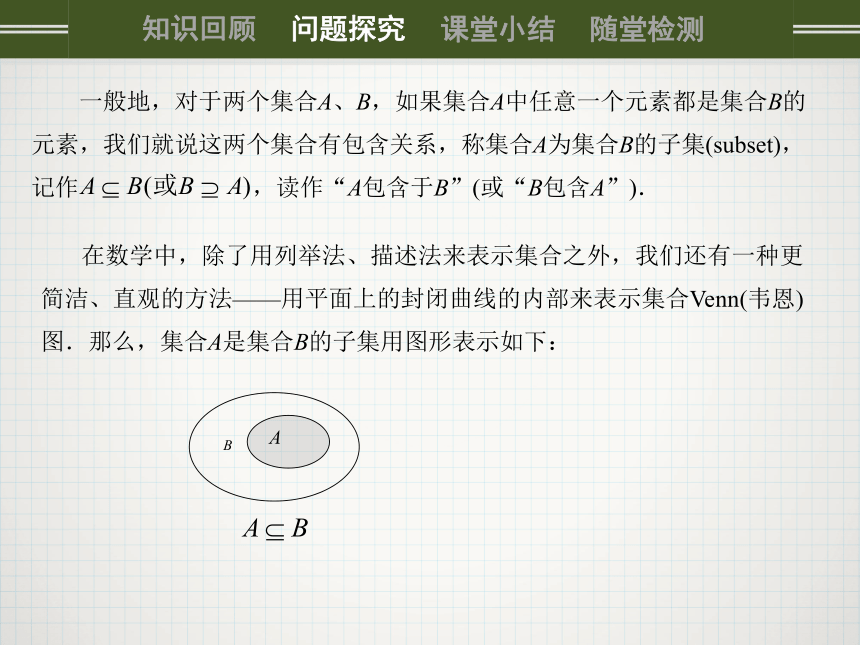
一般地,对于两个集合A、B,如果集合A中任意一个元素都是集合B的元素,我们就说这两个集合有包含关系,称集合A为集合B的子集(subset),记作 ,读作“A包含于B”(或“B包含A”).
在数学中,除了用列举法、描述法来表示集合之外,我们还有一种更简洁、直观的方法——用平面上的封闭曲线的内部来表示集合Venn(韦恩)图.那么,集合A是集合B的子集用图形表示如下:
知识回顾
问题探究
课堂小结
随堂检测
●活动② 归纳提炼集合相等的概念
观察下面4个例子,各对集合中,有没有包含关系?
(1)A={1,3,5},B={5,1,3};
(2)C={1},D={x︱x-1=0};
(3)E={x︱x是等腰三角形},F={x︱x是两条边相等的三角形};
(4)G={x︱x>2},H={x︱2x-1≥3}.
显然,A是B的子集,C是D的子集,E是F的子集,G是H的子集.反过来,B是A的子集,D是C的子集,F是E的子集,H是G的子集.
一般地,如果集合A是集合B的子集( ),且集合B是集合A的子集( ),此时,集合A与集合B的元素是一样的,因此集合A与集合B相等,记作A=B.
知识回顾
问题探究
课堂小结
随堂检测
●活动③ 归纳提炼真子集的概念
问题1:若 ,则集合A与B一定相等吗?
不一定,比如活动②中的四个例子.
问题2:若 ,则可能有A=B,也可能A≠B.当 ,且A≠B时,我们如何进行数学解释?
如果 ,但存在元素 ,我们称集合A是集合B的真子集,记作A B(或B A).
知识回顾
问题探究
课堂小结
随堂检测
●活动④ 归纳提炼空集的概念
观察下面2个集合,它们有何共同特点?
(1)
(2)
显然,这两个集合中都没有元素.
我们把不含任何元素的集合叫空集,记作 .
规定:空集是任何集合的子集,即
空集是任何非空集合的真子集,即
知识回顾
问题探究
课堂小结
随堂检测
●活动⑤ 类比实数大小关系,归纳子集基本性质
知识回顾
问题探究
课堂小结
随堂检测
探究三:识别给定集合的子集,判断给定集合间的关系★▲
●活动① 基础型例题
填写下表,并回答问题
由此猜想,含n个元素的集合的所有子集的个数是多少?真子集的个数、非空子集及非空真子集个数呢?
【思路点拨】按子集元素个数为标准进行分类.
【解题过程】 的子集只有它本身,子集有1个.
{a}的子集为: ,{a};子集共2个.
{a,b}的子集为: ,{a},{b},{a,b};子集共4个.
{a,b,c}的子集为: ,{a},{b},{c},{a,b},{a,c},{b,c},{a,b,c};子集共8个.
知识回顾
问题探究
课堂小结
随堂检测
【答案】
有n个元素的集合,含有2n个子集,2n-1个真子集,2n-1个非空子集,n个元素的非空真子集有2n-2个.
知识回顾
问题探究
课堂小结
随堂检测
例2 判断下列关系是否正确.
(1){1,2} {1,2,3}; (2){1,2,3} {1,2,4}; (3) {a} {a};
(4) ; (5) ; (6) .
【思路点拨】通过子集、真子集、集合相等的含义及集合性质做出正确判断.
【解题过程】(1)集合{1,2}中的元素1、2都是集合{1,2,3}的元素,而集合{1,2,3}中的元素3不是集合{1,2}的元素,故{1,2} {1,2,3}正确;
(2)因为 ,所以{1,2,3} {1,2,4}错误;
(3)任何一个集合是它本身的子集,因此 正确;
(4) 中没有任何元素,而{0}中有一个元素,两者不相等,故 ={0}错误;
(5)空集是任何非空集合的真子集,因此 {0}正确;
(6)空集是任何集合的子集,因此 正确.
【答案】(1)、(3)、(5)、(6)正确,(2)、(4)错误.
知识回顾
问题探究
课堂小结
随堂检测
●活动② 提升型例题
例3 已知集合 , ,则A与B的关系为________.
【思路点拨】通过列举法和特征性质法两种不同的方法进行分析,均可得到集合A、B之间的关系.
【解题过程】方法一:(列举法)
故A B.
对于集合A,取k=…,0,1,2,3,…,得A={…, , , , ,…}.
对于集合B,取k=…,0,1,2,3,4,5,…,
得B={…,0, ,1, ,2, ,…}.
方法二:(特征性质法)
集合A: ,分子为奇数.
集合B: ,分子为整数.
故A B.
知识回顾
问题探究
课堂小结
随堂检测
例4 设集合 , 且 ,求实数k的取值范围.
【思路点拨】关注真子集的含义,结合图形解决.
【解题过程】因为 ,所以 或 .
当 时,有 ,解得 .
当 时,有 解得 .
综上, 或 .
知识回顾
问题探究
课堂小结
随堂检测
●活动③ 探究型例题
例5 已知集合 , ,是否存在实数x,使得集合B是A的子集?若存在,求出A,B,若不存在,说明理由.
【思路点拨】结合集合的确定性、互异性、无序性分清况讨论x的值和集合A、B.
【解题过程】因为B A,所以x+2=3或 .
当x+2=3,即x=1时,A={1,3,1}不满足互异性.
当 ,即x=2或x=-1.
若x=2时,A={1,3,4},B={1,4},满足B A.
若x=-1时,A={1,3,1}不满足互异性.
综上,存在x=2使得B A.
此时,A={1,3,4},B={1,4}.
【答案】存在x=2使得B A.此时,A={1,3,4},B={1,4}.
知识梳理
知识回顾
问题探究
课堂小结
随堂检测
(4)把不含任何元素的集合叫空集,记作 .
(1)一般地,对于两个集合A、B,如果集合A中任意一个元素都是集合B的元素,我们就说这两个集合有包含关系,称集合A为集合B的子集(subset),记作 ,读作“A包含于B”(或“B包含A”).
(2)如果集合A是集合B的子集( ),且集合B是集合A的子集( ),此时,集合A与集合B的元素是一样的,因此集合A与集合B相等,记作A=B .
(3)如果 ,但存在元素 ,我们称集合A是集合B的真子集,记作A B(或B A).
(5)空集是任何集合的子集,即 ;空集是任何集合的真子集,即
A;任何一个集合都是它自己的子集,即 ; 对于集合A、B、C,如果 且 ,那么 .
重难点突破
知识回顾
问题探究
课堂小结
随堂检测
(1)元素与集合间的关系用“∈”、“ ”来表示,集合与集合间的关系用“ ”、“ ”、“=”来表示.
(2)集合与集合间的关系涉及到含参数问题时,要注意分类讨论,并能用元素的互异性进行检验.
知识回顾
问题探究
课堂小结
随堂检测
点击“随堂训练”
选择“《集合间的基本关系》随堂检测”
配套课后作业:
《集合间的基本关系》基础型
《集合间的基本关系》能力型
《集合间的基本关系》探究型
《集合间的基本关系》自助餐
名 师 课 件
集合间的基本关系
知识回顾
问题探究
课堂小结
随堂检测
检测下预习效果:
点击“随堂训练”
选择“《集合间的基本关系》预习自测”
一般地,我们把研究对象统称为元素,把一些元素组成的总体叫做集合.只要构成两个集合的元素是一样的,我们就称这两个集合是相等的.
如果a是集合A中的元素,就说a属于集合A,记作a∈A;如果a不是集合A中的元素,就说a不属于集合A,记作a A.
除了用自然语言表示集合,还能用列举法、描述法表示集合.
知识回顾
问题探究
课堂小结
随堂检测
探究一:回顾旧知,提出新问
●活动① 回顾旧知
问题:元素与集合之间的关系应如何表示?(可举例进行说明)
元素与集合间是“∈”或“ ”的关系,如1∈{1,2,3};0 {1,2,3}等.
●活动② 创设情境,提出问题
对两个数a、b,应有a>b或a
问题探究
课堂小结
随堂检测
探究二:探究集合间的关系、集合的子集以及集合的性质★▲
●活动① 归纳提炼子集的概念
观察下面4个例子,指出给定两个集合中的元素有什么关系?每个例子中的两个集合又有什么关系呢?
(1)A={1,2,3},B={1,2,3,4,5,6};
(2)C={新华中学高一(2)班全体女生},
D={新华中学高一(2)班全体学生};
(3)E={x︱x是等边三角形},F={x︱x是三角形};
(4)G={x︱x>2},H={x︱2x-1≥3}.
我们可以看到,(1)中的集合A中的任何元素都是集合B的元素,(2)中的集合C中的元素都是集合D中的元素,(3)中的集合E的任何元素都是集合F的元素,(4)中的集合G中的任何元素都是集合H中的元素.
知识回顾
问题探究
课堂小结
随堂检测
一般地,对于两个集合A、B,如果集合A中任意一个元素都是集合B的元素,我们就说这两个集合有包含关系,称集合A为集合B的子集(subset),记作 ,读作“A包含于B”(或“B包含A”).
在数学中,除了用列举法、描述法来表示集合之外,我们还有一种更简洁、直观的方法——用平面上的封闭曲线的内部来表示集合Venn(韦恩)图.那么,集合A是集合B的子集用图形表示如下:
知识回顾
问题探究
课堂小结
随堂检测
●活动② 归纳提炼集合相等的概念
观察下面4个例子,各对集合中,有没有包含关系?
(1)A={1,3,5},B={5,1,3};
(2)C={1},D={x︱x-1=0};
(3)E={x︱x是等腰三角形},F={x︱x是两条边相等的三角形};
(4)G={x︱x>2},H={x︱2x-1≥3}.
显然,A是B的子集,C是D的子集,E是F的子集,G是H的子集.反过来,B是A的子集,D是C的子集,F是E的子集,H是G的子集.
一般地,如果集合A是集合B的子集( ),且集合B是集合A的子集( ),此时,集合A与集合B的元素是一样的,因此集合A与集合B相等,记作A=B.
知识回顾
问题探究
课堂小结
随堂检测
●活动③ 归纳提炼真子集的概念
问题1:若 ,则集合A与B一定相等吗?
不一定,比如活动②中的四个例子.
问题2:若 ,则可能有A=B,也可能A≠B.当 ,且A≠B时,我们如何进行数学解释?
如果 ,但存在元素 ,我们称集合A是集合B的真子集,记作A B(或B A).
知识回顾
问题探究
课堂小结
随堂检测
●活动④ 归纳提炼空集的概念
观察下面2个集合,它们有何共同特点?
(1)
(2)
显然,这两个集合中都没有元素.
我们把不含任何元素的集合叫空集,记作 .
规定:空集是任何集合的子集,即
空集是任何非空集合的真子集,即
知识回顾
问题探究
课堂小结
随堂检测
●活动⑤ 类比实数大小关系,归纳子集基本性质
知识回顾
问题探究
课堂小结
随堂检测
探究三:识别给定集合的子集,判断给定集合间的关系★▲
●活动① 基础型例题
填写下表,并回答问题
由此猜想,含n个元素的集合的所有子集的个数是多少?真子集的个数、非空子集及非空真子集个数呢?
【思路点拨】按子集元素个数为标准进行分类.
【解题过程】 的子集只有它本身,子集有1个.
{a}的子集为: ,{a};子集共2个.
{a,b}的子集为: ,{a},{b},{a,b};子集共4个.
{a,b,c}的子集为: ,{a},{b},{c},{a,b},{a,c},{b,c},{a,b,c};子集共8个.
知识回顾
问题探究
课堂小结
随堂检测
【答案】
有n个元素的集合,含有2n个子集,2n-1个真子集,2n-1个非空子集,n个元素的非空真子集有2n-2个.
知识回顾
问题探究
课堂小结
随堂检测
例2 判断下列关系是否正确.
(1){1,2} {1,2,3}; (2){1,2,3} {1,2,4}; (3) {a} {a};
(4) ; (5) ; (6) .
【思路点拨】通过子集、真子集、集合相等的含义及集合性质做出正确判断.
【解题过程】(1)集合{1,2}中的元素1、2都是集合{1,2,3}的元素,而集合{1,2,3}中的元素3不是集合{1,2}的元素,故{1,2} {1,2,3}正确;
(2)因为 ,所以{1,2,3} {1,2,4}错误;
(3)任何一个集合是它本身的子集,因此 正确;
(4) 中没有任何元素,而{0}中有一个元素,两者不相等,故 ={0}错误;
(5)空集是任何非空集合的真子集,因此 {0}正确;
(6)空集是任何集合的子集,因此 正确.
【答案】(1)、(3)、(5)、(6)正确,(2)、(4)错误.
知识回顾
问题探究
课堂小结
随堂检测
●活动② 提升型例题
例3 已知集合 , ,则A与B的关系为________.
【思路点拨】通过列举法和特征性质法两种不同的方法进行分析,均可得到集合A、B之间的关系.
【解题过程】方法一:(列举法)
故A B.
对于集合A,取k=…,0,1,2,3,…,得A={…, , , , ,…}.
对于集合B,取k=…,0,1,2,3,4,5,…,
得B={…,0, ,1, ,2, ,…}.
方法二:(特征性质法)
集合A: ,分子为奇数.
集合B: ,分子为整数.
故A B.
知识回顾
问题探究
课堂小结
随堂检测
例4 设集合 , 且 ,求实数k的取值范围.
【思路点拨】关注真子集的含义,结合图形解决.
【解题过程】因为 ,所以 或 .
当 时,有 ,解得 .
当 时,有 解得 .
综上, 或 .
知识回顾
问题探究
课堂小结
随堂检测
●活动③ 探究型例题
例5 已知集合 , ,是否存在实数x,使得集合B是A的子集?若存在,求出A,B,若不存在,说明理由.
【思路点拨】结合集合的确定性、互异性、无序性分清况讨论x的值和集合A、B.
【解题过程】因为B A,所以x+2=3或 .
当x+2=3,即x=1时,A={1,3,1}不满足互异性.
当 ,即x=2或x=-1.
若x=2时,A={1,3,4},B={1,4},满足B A.
若x=-1时,A={1,3,1}不满足互异性.
综上,存在x=2使得B A.
此时,A={1,3,4},B={1,4}.
【答案】存在x=2使得B A.此时,A={1,3,4},B={1,4}.
知识梳理
知识回顾
问题探究
课堂小结
随堂检测
(4)把不含任何元素的集合叫空集,记作 .
(1)一般地,对于两个集合A、B,如果集合A中任意一个元素都是集合B的元素,我们就说这两个集合有包含关系,称集合A为集合B的子集(subset),记作 ,读作“A包含于B”(或“B包含A”).
(2)如果集合A是集合B的子集( ),且集合B是集合A的子集( ),此时,集合A与集合B的元素是一样的,因此集合A与集合B相等,记作A=B .
(3)如果 ,但存在元素 ,我们称集合A是集合B的真子集,记作A B(或B A).
(5)空集是任何集合的子集,即 ;空集是任何集合的真子集,即
A;任何一个集合都是它自己的子集,即 ; 对于集合A、B、C,如果 且 ,那么 .
重难点突破
知识回顾
问题探究
课堂小结
随堂检测
(1)元素与集合间的关系用“∈”、“ ”来表示,集合与集合间的关系用“ ”、“ ”、“=”来表示.
(2)集合与集合间的关系涉及到含参数问题时,要注意分类讨论,并能用元素的互异性进行检验.
知识回顾
问题探究
课堂小结
随堂检测
点击“随堂训练”
选择“《集合间的基本关系》随堂检测”
配套课后作业:
《集合间的基本关系》基础型
《集合间的基本关系》能力型
《集合间的基本关系》探究型
《集合间的基本关系》自助餐
