华东师大版八年级数学下册第19章矩形、菱形与正方形测试题(word版含答案)
文档属性
| 名称 | 华东师大版八年级数学下册第19章矩形、菱形与正方形测试题(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 128.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-31 11:43:07 | ||
图片预览




文档简介
第19章 矩形、菱形与正方形
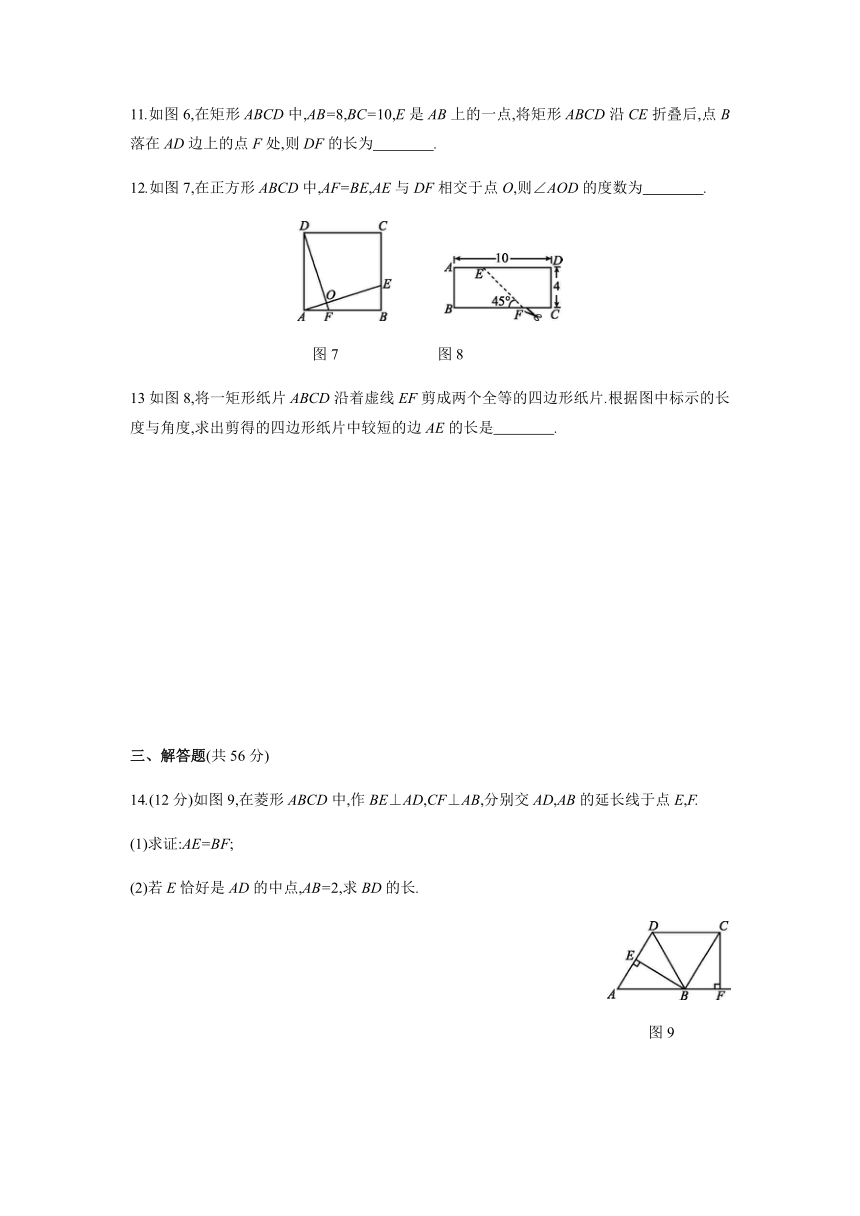
一、选择题
1.菱形、矩形、正方形都具有的性质是 ( )
A.四条边相等,四个角相等 B.对角线相等
C.对角线互相垂直 D.对角线互相平分
2.如果平行四边形的四个内角的平分线能够围成一个四边形,那么这个四边形一定是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
3.如图1,在矩形ABCD中,对角线AC,BD相交于点O,∠ACB=30°,则∠AOB的度数为 ( )
A.30° B.60° C.90° D.120°
图1 图2
4.如图2,在矩形ABCD中,DE平分∠ADC交BC于点E,EF⊥AD于点F.若EF=3,AE=5,则AD的长为 ( )
A.5 B.6 C.7 D.8
5.在 ABCD中,对角线AC,BD相交于点O,给出下列条件:①∠ABC=90°;②AC⊥BD;③AB=BC;④AC平分∠BAD;⑤AO=DO.其中能使 ABCD为菱形的条件有 ( )
A.①②③ B.②③④ C.③④⑤ D.①②⑤
6.如图3,四边形ABCD是正方形,直线a,b,c分别通过点A,D,C,且a∥b∥c.若a与b之间的距离是3,b与c之间的距离是6,则正方形ABCD的面积是 ( )
图3
A.36 B.45 C.54 D.64
7如图4,四边形ABCD是菱形,E,F分别是边BC,CD上的点,添加下列条件后,不能保证△ABE和△ADF全等的是 ( )
A.∠BAF=∠DAE B.EC=FC
C.AE=AF D.BE=DF
图4 图5
8如图5,在菱形ABCD中,AB=2,∠A=120°,过菱形ABCD的对称中心O分别作边AB,BC的垂线,交各边于点E,G,F,H,则四边形EFGH的周长为 ( )
A.3+ B.2+ C.2+ D.1+
二、填空题
9.如图4,在菱形ABCD中,已知∠ABD=20°,则∠C= °.
图4
10.如图5,在∠MON的两边上分别截取OA,OB,使OA=OB,分别以点A,B为圆心,OA长为半径作弧,两弧交于点C,连结AC,BC,AB,OC.若AB=2 cm,四边形OACB的面积为4 cm2,则OC的长为 cm.
图5 图6
11.如图6,在矩形ABCD中,AB=8,BC=10,E是AB上的一点,将矩形ABCD沿CE折叠后,点B落在AD边上的点F处,则DF的长为 .
12.如图7,在正方形ABCD中,AF=BE,AE与DF相交于点O,则∠AOD的度数为 .
图7 图8
13如图8,将一矩形纸片ABCD沿着虚线EF剪成两个全等的四边形纸片.根据图中标示的长度与角度,求出剪得的四边形纸片中较短的边AE的长是 .
三、解答题(共56分)
14.(12分)如图9,在菱形ABCD中,作BE⊥AD,CF⊥AB,分别交AD,AB的延长线于点E,F.
(1)求证:AE=BF;
(2)若E恰好是AD的中点,AB=2,求BD的长.
图9
15.(14分)如图10,在矩形ABCD中,点E在AD上,EC平分∠BED.
(1)△BEC是不是等腰三角形 为什么
(2)若AB=1,∠ABE=45°,求BC的长.
图10
16.(14分)如图11,在△ABC中,AB=AC,∠BAC=40°,将△ABC绕点A按逆时针方向旋转100°,得到△ADE,连结BD,CE交于点F.
求证:(1)△ABD≌△ACE;
(2)四边形ABFE是菱形.
图11
17.(16分)已知:如图12, ABCD的对角线AC,BD相交于点O,若AC=20 cm,BD=12 cm,两动点E,F以2 cm/s的速度分别从点A,C同时出发在线段AC上运动,点E到达点C,点F到达点A时停止运动.
(1)求证:当点E,F在运动过程中且不与点O重合时,四边形BEDF一定为平行四边形;
(2)当点E,F的运动时间为多少时,四边形BEDF为矩形
图12
18.如图四边形ABCD是正方形,点E,F分别在BC,AB上,点M在BA的延长线上,且CE=BF=AM,分别过点M,E作NM⊥DM,NE⊥DE,NM与NE交于点N,连结NF,CF.
(1)求证:DE⊥DM;
(2)猜想四边形CENF是怎样的特殊四边形,并证明你的猜想.
答案
1.D 2.B 3.B 4.C 5.B 6.B 7.C 8.A
9.140
10 .4
11.6
12.90°
13.3
14.解:(1)证明:∵四边形ABCD是菱形,
∴AB=BC,AD∥BC,∴∠A=∠CBF.
∵BE⊥AD,CF⊥AB,∴∠AEB=∠BFC=90°,
∴△AEB≌△BFC(A.A.S.),∴AE=BF.
(2)∵E是AD的中点,且BE⊥AD,
∴直线BE为线段AD的垂直平分线,∴BD=AB=2.
15.解:(1)△BEC是等腰三角形.
理由:∵四边形ABCD是矩形,
∴AD∥BC,∴∠DEC=∠BCE.
∵EC平分∠BED,
∴∠BEC=∠DEC,∴∠BEC=∠BCE,
∴BE=BC,
∴△BEC是等腰三角形.
(2)∵在Rt△ABE中,∠ABE=45°,
∴AE=AB=1,
∴BE===,
∴BC=BE=.
16.证明:(1)∵△ABC绕点A按逆时针方向旋转100°得到△ADE,
∴△ABC≌△ADE,∠BAD=∠CAE=100°.
又∵AB=AC,∴AB=AC=AD=AE.
在△ABD与△ACE中,
∵AB=AC,∠BAD=∠CAE,AD=AE,
∴△ABD≌△ACE.
(2)∵∠BAD=∠CAE=100°,AB=AC=AD=AE,
∴∠ABD=∠ADB=∠ACE=∠AEC=40°.
∵∠BAE=∠BAC+∠CAE=40°+100°=140°,
∴∠ABD+∠BAE=180°,∠BAE+∠AEC=180°,
∴AE∥BF,AB∥EF,
∴四边形ABFE是平行四边形.
又∵AB=AE,∴四边形ABFE是菱形.
17.解:(1)证明:∵两动点E,F以2 cm/s的速度分别从点A,C同时出发在线段AC上运动,∴AE=CF.
∵四边形ABCD是平行四边形,
∴OD=OB,OA=OC(平行四边形的对角线互相平分),
∴OA-AE=OC-CF或AE-OA=CF-OC,
即OE=OF,
∴四边形BEDF为平行四边形(对角线互相平分的四边形是平行四边形),
即当点E,F在运动过程中且不与点O重合时, 四边形BEDF一定为平行四边形.
(2)分情况讨论:①当点E在OA上,点F在OC上,且EF=BD=12 cm时,四边形BEDF为矩形.
设点E,F的运动时间为t1 s,则AE=CF=2t1 cm,
∴EF=(20-4t1)cm,
则20-4t1=12,解得t1=2.
②当点E在OC上,点F在OA上,且EF=BD=12 cm时,四边形BEDF为矩形.
设点E,F的运动时间为t2 s,则AE=CF=2t2 cm,
∴EF=2t2-(20-2t2)=(4t2-20)cm,
则4t2-20=12,解得t2=8.
因此,当点E,F的运动时间为2 s或8 s时,四边形BEDF为矩形.
18.解:(1)证明:∵四边形ABCD是正方形,
∴DC=DA,∠ADC=∠DCE=∠DAM=90°.
在△DCE和△DAM中,
∵DC=DA,∠DCE=∠DAM,CE=AM,
∴△DCE≌△DAM,∴∠EDC=∠MDA.
又∵∠ADE+∠EDC=∠ADC=90°,
∴∠ADE+∠MDA=90°,∴DE⊥DM.
(2)四边形CENF是平行四边形.
证明:∵四边形ABCD是正方形,
∴AB∥CD,AB=CD.
∵BF=AM,
∴MF=AF+AM=AF+BF=AB,
即MF=CD.
又∵点F在AB上,点M在BA的延长线上,
∴MF∥CD,∴四边形CFMD是平行四边形,
∴DM=CF,DM∥CF.
∵NM⊥DM,NE⊥DE,DE⊥DM,
∴四边形DENM是矩形,
∴EN=DM,EN∥DM,
∴CF=EN,CF∥EN,
∴四边形CENF是平行四边形.
一、选择题
1.菱形、矩形、正方形都具有的性质是 ( )
A.四条边相等,四个角相等 B.对角线相等
C.对角线互相垂直 D.对角线互相平分
2.如果平行四边形的四个内角的平分线能够围成一个四边形,那么这个四边形一定是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
3.如图1,在矩形ABCD中,对角线AC,BD相交于点O,∠ACB=30°,则∠AOB的度数为 ( )
A.30° B.60° C.90° D.120°
图1 图2
4.如图2,在矩形ABCD中,DE平分∠ADC交BC于点E,EF⊥AD于点F.若EF=3,AE=5,则AD的长为 ( )
A.5 B.6 C.7 D.8
5.在 ABCD中,对角线AC,BD相交于点O,给出下列条件:①∠ABC=90°;②AC⊥BD;③AB=BC;④AC平分∠BAD;⑤AO=DO.其中能使 ABCD为菱形的条件有 ( )
A.①②③ B.②③④ C.③④⑤ D.①②⑤
6.如图3,四边形ABCD是正方形,直线a,b,c分别通过点A,D,C,且a∥b∥c.若a与b之间的距离是3,b与c之间的距离是6,则正方形ABCD的面积是 ( )
图3
A.36 B.45 C.54 D.64
7如图4,四边形ABCD是菱形,E,F分别是边BC,CD上的点,添加下列条件后,不能保证△ABE和△ADF全等的是 ( )
A.∠BAF=∠DAE B.EC=FC
C.AE=AF D.BE=DF
图4 图5
8如图5,在菱形ABCD中,AB=2,∠A=120°,过菱形ABCD的对称中心O分别作边AB,BC的垂线,交各边于点E,G,F,H,则四边形EFGH的周长为 ( )
A.3+ B.2+ C.2+ D.1+
二、填空题
9.如图4,在菱形ABCD中,已知∠ABD=20°,则∠C= °.
图4
10.如图5,在∠MON的两边上分别截取OA,OB,使OA=OB,分别以点A,B为圆心,OA长为半径作弧,两弧交于点C,连结AC,BC,AB,OC.若AB=2 cm,四边形OACB的面积为4 cm2,则OC的长为 cm.
图5 图6
11.如图6,在矩形ABCD中,AB=8,BC=10,E是AB上的一点,将矩形ABCD沿CE折叠后,点B落在AD边上的点F处,则DF的长为 .
12.如图7,在正方形ABCD中,AF=BE,AE与DF相交于点O,则∠AOD的度数为 .
图7 图8
13如图8,将一矩形纸片ABCD沿着虚线EF剪成两个全等的四边形纸片.根据图中标示的长度与角度,求出剪得的四边形纸片中较短的边AE的长是 .
三、解答题(共56分)
14.(12分)如图9,在菱形ABCD中,作BE⊥AD,CF⊥AB,分别交AD,AB的延长线于点E,F.
(1)求证:AE=BF;
(2)若E恰好是AD的中点,AB=2,求BD的长.
图9
15.(14分)如图10,在矩形ABCD中,点E在AD上,EC平分∠BED.
(1)△BEC是不是等腰三角形 为什么
(2)若AB=1,∠ABE=45°,求BC的长.
图10
16.(14分)如图11,在△ABC中,AB=AC,∠BAC=40°,将△ABC绕点A按逆时针方向旋转100°,得到△ADE,连结BD,CE交于点F.
求证:(1)△ABD≌△ACE;
(2)四边形ABFE是菱形.
图11
17.(16分)已知:如图12, ABCD的对角线AC,BD相交于点O,若AC=20 cm,BD=12 cm,两动点E,F以2 cm/s的速度分别从点A,C同时出发在线段AC上运动,点E到达点C,点F到达点A时停止运动.
(1)求证:当点E,F在运动过程中且不与点O重合时,四边形BEDF一定为平行四边形;
(2)当点E,F的运动时间为多少时,四边形BEDF为矩形
图12
18.如图四边形ABCD是正方形,点E,F分别在BC,AB上,点M在BA的延长线上,且CE=BF=AM,分别过点M,E作NM⊥DM,NE⊥DE,NM与NE交于点N,连结NF,CF.
(1)求证:DE⊥DM;
(2)猜想四边形CENF是怎样的特殊四边形,并证明你的猜想.
答案
1.D 2.B 3.B 4.C 5.B 6.B 7.C 8.A
9.140
10 .4
11.6
12.90°
13.3
14.解:(1)证明:∵四边形ABCD是菱形,
∴AB=BC,AD∥BC,∴∠A=∠CBF.
∵BE⊥AD,CF⊥AB,∴∠AEB=∠BFC=90°,
∴△AEB≌△BFC(A.A.S.),∴AE=BF.
(2)∵E是AD的中点,且BE⊥AD,
∴直线BE为线段AD的垂直平分线,∴BD=AB=2.
15.解:(1)△BEC是等腰三角形.
理由:∵四边形ABCD是矩形,
∴AD∥BC,∴∠DEC=∠BCE.
∵EC平分∠BED,
∴∠BEC=∠DEC,∴∠BEC=∠BCE,
∴BE=BC,
∴△BEC是等腰三角形.
(2)∵在Rt△ABE中,∠ABE=45°,
∴AE=AB=1,
∴BE===,
∴BC=BE=.
16.证明:(1)∵△ABC绕点A按逆时针方向旋转100°得到△ADE,
∴△ABC≌△ADE,∠BAD=∠CAE=100°.
又∵AB=AC,∴AB=AC=AD=AE.
在△ABD与△ACE中,
∵AB=AC,∠BAD=∠CAE,AD=AE,
∴△ABD≌△ACE.
(2)∵∠BAD=∠CAE=100°,AB=AC=AD=AE,
∴∠ABD=∠ADB=∠ACE=∠AEC=40°.
∵∠BAE=∠BAC+∠CAE=40°+100°=140°,
∴∠ABD+∠BAE=180°,∠BAE+∠AEC=180°,
∴AE∥BF,AB∥EF,
∴四边形ABFE是平行四边形.
又∵AB=AE,∴四边形ABFE是菱形.
17.解:(1)证明:∵两动点E,F以2 cm/s的速度分别从点A,C同时出发在线段AC上运动,∴AE=CF.
∵四边形ABCD是平行四边形,
∴OD=OB,OA=OC(平行四边形的对角线互相平分),
∴OA-AE=OC-CF或AE-OA=CF-OC,
即OE=OF,
∴四边形BEDF为平行四边形(对角线互相平分的四边形是平行四边形),
即当点E,F在运动过程中且不与点O重合时, 四边形BEDF一定为平行四边形.
(2)分情况讨论:①当点E在OA上,点F在OC上,且EF=BD=12 cm时,四边形BEDF为矩形.
设点E,F的运动时间为t1 s,则AE=CF=2t1 cm,
∴EF=(20-4t1)cm,
则20-4t1=12,解得t1=2.
②当点E在OC上,点F在OA上,且EF=BD=12 cm时,四边形BEDF为矩形.
设点E,F的运动时间为t2 s,则AE=CF=2t2 cm,
∴EF=2t2-(20-2t2)=(4t2-20)cm,
则4t2-20=12,解得t2=8.
因此,当点E,F的运动时间为2 s或8 s时,四边形BEDF为矩形.
18.解:(1)证明:∵四边形ABCD是正方形,
∴DC=DA,∠ADC=∠DCE=∠DAM=90°.
在△DCE和△DAM中,
∵DC=DA,∠DCE=∠DAM,CE=AM,
∴△DCE≌△DAM,∴∠EDC=∠MDA.
又∵∠ADE+∠EDC=∠ADC=90°,
∴∠ADE+∠MDA=90°,∴DE⊥DM.
(2)四边形CENF是平行四边形.
证明:∵四边形ABCD是正方形,
∴AB∥CD,AB=CD.
∵BF=AM,
∴MF=AF+AM=AF+BF=AB,
即MF=CD.
又∵点F在AB上,点M在BA的延长线上,
∴MF∥CD,∴四边形CFMD是平行四边形,
∴DM=CF,DM∥CF.
∵NM⊥DM,NE⊥DE,DE⊥DM,
∴四边形DENM是矩形,
∴EN=DM,EN∥DM,
∴CF=EN,CF∥EN,
∴四边形CENF是平行四边形.
