人教版数学七年级下册5.2.1平行线课件(共42张PPT)
文档属性
| 名称 | 人教版数学七年级下册5.2.1平行线课件(共42张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-31 14:38:22 | ||
图片预览







文档简介
(共42张PPT)
人教版 · 数学· 七年级(下)
第5章 相交线与平行线
5.2.1 平行线
1.了解两条直线的平行关系,掌握有关的符号表示。
2.学会用三角尺、量角器画平行线。
3.掌握平行公理及其推论,培养空间想象能力。
学习目标
如图,分别将木条a、b与木条c钉在一起,并把它们想象成在同一平面内两端可以无限延伸的三条直线.转动a,直线a从在c的左侧与直线b相交逐步变为在c的右侧与b相交.想象一下,在这个过程中,有没有直线a与直线b不相交的位置呢?
a
b
c
a
b
c
a
b
c
新知一 平行线的定义及表示
合作探究
在木条转动过程中,存在一个直线a与直线b不相交的位置,这时我们说直线a与b互相平行.
平行线在生活中是很常见的,你还能举出其他一些例子吗?
在木条转动过程中,存在直线a与直线b不相交的情形,这时我们说直线a与b互相平行.记作“a∥b”.
在同一平面内,不相交的两条直线叫做平行线.
注意:平行线的定义包含三层意思:
(1)“在同一平面内”是前提条件;
(2)“不相交”就是说两条直线没有交点;
(3)平行线指的是“两条直线”而不是两条射线或两条线段.
平行线的概念
a
b
c
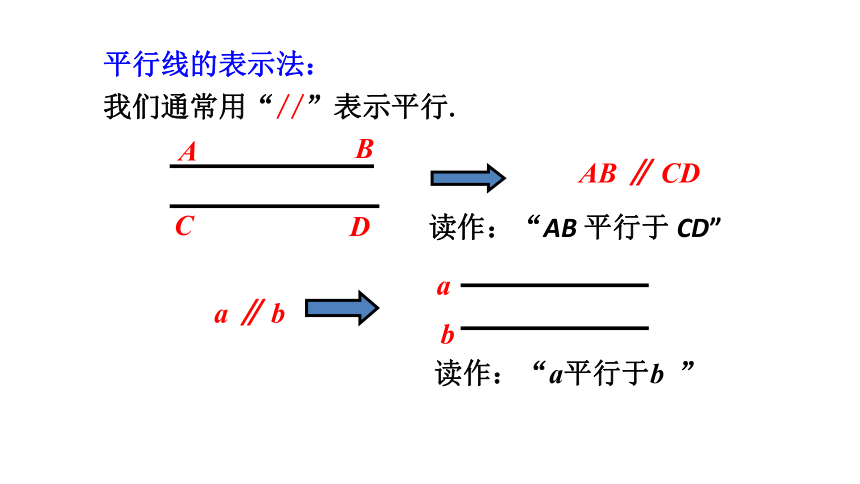
我们通常用“//”表示平行.
C
B
A
D
a ∥ b
AB ∥ CD
a
b
读作:“AB 平行于 CD”
读作:“a平行于b ”
平行线的表示法:
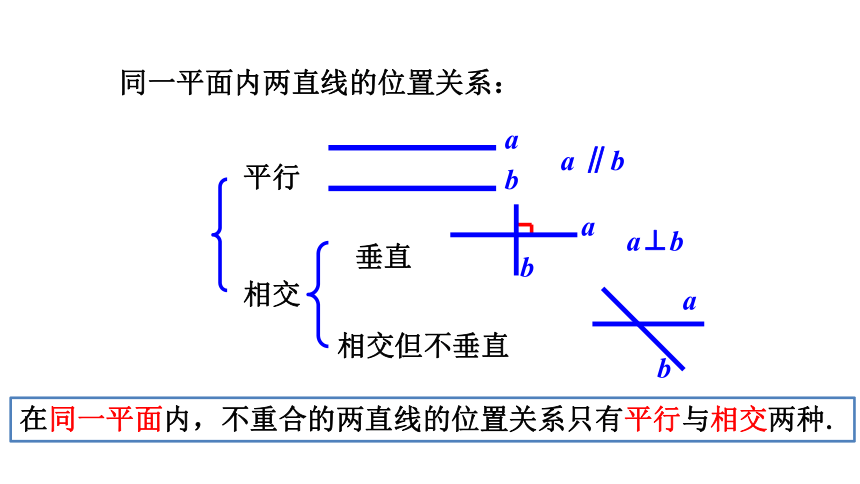
同一平面内两直线的位置关系:
平行
相交
垂直
相交但不垂直
a
b
a⊥b
a ∥b
a
b
b
a
在同一平面内,不重合的两直线的位置关系只有平行与相交两种.
例 下列说法正确的是( )
A.两条不相交的直线一定相互平行
B.在同一平面内,两条不平行的直线一定相交
C.在同一平面内,两条不相交的线段一定平行
D.在同一平面内,两条不相交的射线互相平行
B
典例精析 平行线的识别
下列说法中,正确的个数有( )
(1)在同一平面内不相交的两条线段必平行
(2)在同一平面内不相交的两条直线必平行
(3)在同一平面内不平行的两条线段必相交
(4)在同一平面内不平行的两条直线必相交
A.1个 B.2个 C.3个 D.4个
B
√
×
×
√
巩固新知
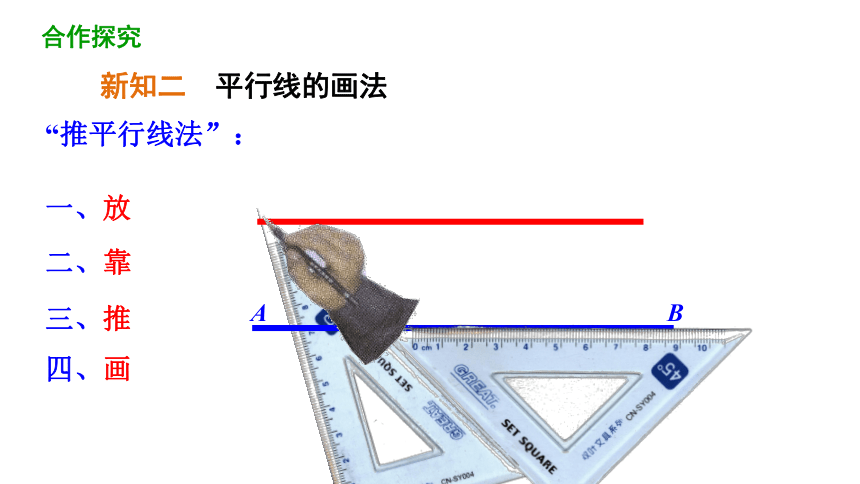
一、放
二、靠
三、推
四、画
B
A
新知二 平行线的画法
“推平行线法”:
合作探究
●
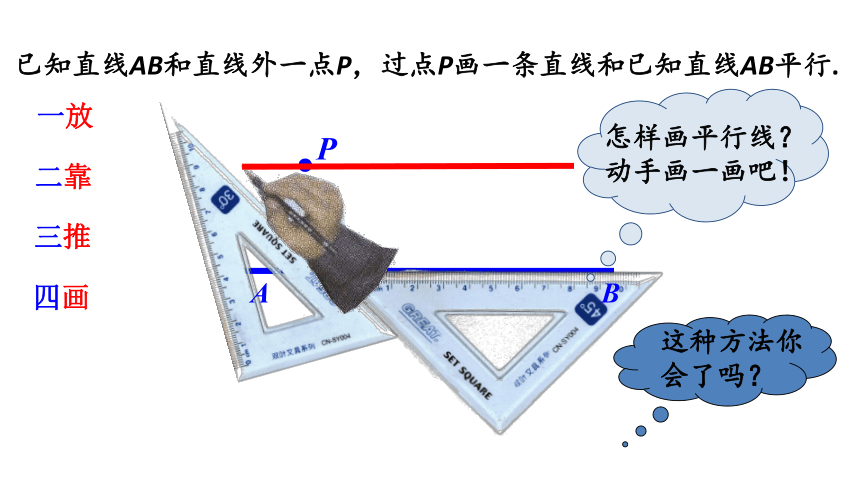
一放
二靠
三推
四画
怎样画平行线?动手画一画吧!
这种方法你会了吗?
已知直线AB和直线外一点P,过点P画一条直线和已知直线AB平行.
P
B
A
A
B
P
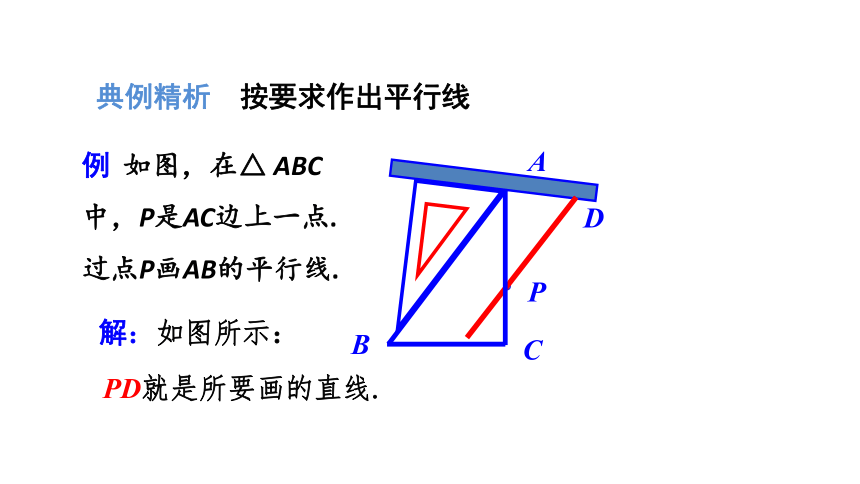
例 如图,在△ ABC中,P是AC边上一点.过点P画AB的平行线.
C
D
解:如图所示:
典例精析 按要求作出平行线
PD就是所要画的直线.
A
B
P
如图,在△ABC 中,P是AC边上一点.过点P画BC的平行线.
C
E
解:PE就是所要画的直线.
巩固新知
·
A
·
B
(3)经过点C能画出几条直线与直线AB平行?
(4)过点D画一条直线与直线AB平行,与(3)中所画的直线平行吗?
·
·
C
D
(1)经过点C能画出几条直线?
无数条.
1条.
a
b
(2)与直线AB平行的直线有几条?
无数条.
平行.
你能对这些情况进行归纳总结吗?
新知三 平行公理及其推论
合作探究
平行公理:经过直线外一点,有且只有一条直线与这条
直线平行.
·
A
·
B
·
·
C
D
温馨提示:
(1)平行公理中强调“直线外一点”,若点在直线上,不可能有平行线;
(2)“有且只有”强调这样的直线是存在的,也是唯一的.
几何语言:
c
b
a
平行公理的推论(平行线的传递性):
如果两条直线都与第三条直线平行,那么这两条直线也互相平行.
∵a//c , c//b,
∴ a//b(如果两条直线都和第三条直线平行,那么这两条直线也互相平行).
例 下列说法中,正确的是( )
(1)过一点,有且只有一条直线与已知直线平行;
(2)平行于同一条直线的两条直线互相平行;
(3)一条直线的平行线有且只有一条;
(4)若a∥b,b∥c,则a∥c.
A.(1)(2) B.(2)(3)
C.(1)(3) D.(2)(4)
典例精析 平行公理及其推论的应用
D
×
√
×
√
若AB∥CD,AB∥EF,则__________. 如图所示,MC∥AB,NC∥AB,则点M,C,N在同一条直线上,理由是___________________________________________________
CD∥EF
经过直线外一点,有且只有一条直线与这条直线平行.
巩固新知
1.(4分)下列说法正确的是( )
A.同一平面内,没有公共点的两条线段是平行线
B.同一平面内,两条平行线只有一个公共点
C.同一平面内,没有公共点的两条直线是平行线
D.两条不相交的直线叫做平行线
C
课堂练习
2.(5分)同一平面内,直线AB与直线CD满足下列条件,指出其对应的位置关系.
(1)若直线AB与直线CD没有公共点,则直线AB与直线CD的位置关系为________;
(2)直线AB与直线CD有且只有一个公共点,则直线AB与直线CD的位置关系为__________.
平行
相交
3.(5分)在同一平面内,下列说法中,错误的是( )
A.过两点有且只有一条直线
B.过一点有无数条直线与已知直线平行
C.过直线外一点有且有一条直线与已知直线平行
D.过一点有且只有一条直线与已知直线垂直
B
4.(5分)如图,PC∥AB,QC∥AB,则点P,C,Q在一条直线上,理由是__________________________________________________.
经过直线外一点,有且只有一条直线与这条直线平行
5.(8分)如图,P,Q分别是直线EF外两点.
(1)过点P画直线AB∥EF,过点Q画直线CD∥EF;
(2)AB与CD有怎样的位置关系?为什么?
解:(1)如图
(2)AB∥CD
理由:因为AB∥EF,CD∥EF,
所以AB∥CD
6.(10分)如图所示,取一张长方形的硬纸板ABCD,将硬纸板ABCD对折使CD与AB重合,EF为折痕.把长方形ABFE平放在桌面上,另一个面CDEF无论怎么改变位置总有CD∥AB存在,你知道为什么吗?
解:因为AB∥EF,CD∥EF,所以CD∥AB
【综合运用】
7.(12分)如图,两条直线l1与l2可以把一个平面分成3部分(如图①),也可以把一个平面分成4部分(如图②),若平面内有三条直线,可以把平面分成多少部分?(本题只考虑在同一平面内的情况)
解:可以把平面分成4部分或7部分或6部分,如图
1.在同一平面内,不相交的两条直线叫做平行线.
3.如果两条直线都与第三条直线平行,那么这两条直
线互相平行.
2.经过直线外一点,有且只有一条直线与已知直线平行.
平行公理的推论
平行公理
定义
归纳新知
1.如图,直线AC和直线BD相交于点O,OE平分∠BOC.若∠1+∠2=80°,则∠3的度数为( )
A.40° B.50° C.60° D.70°
D
课后练习
2.如图所示,下列结论中不正确的是( )
A.∠1和∠2是同位角 B.∠2和∠3是同旁内角
C.∠1和∠4是同位角 D.∠2和∠4是内错角
A
3.以下两条直线互相垂直的是( )
①两条直线相交所成的四个角中有一个是直角;②两条直线相交所成的所有邻补角都相等;③两条直线相交,有一组邻补角相等;④两条直线相交,对顶角互补.
A.①③ B.①②③
C.②③④ D.①②③④
D
4.(杭州中考)若线段AM,AN分别是△ABC的BC边上的高线和中线,
则( )
A.AM>AN B.AM≥AN
C.AM<AN D.AM≤AN
D
5.如图,直线AB与CD相交于点O,OP是∠BOC的平分线,OE⊥AB,OF⊥CD.
(1)若∠AOD=50°,请求出∠DOP的度数;
(2)OP平分∠EOF吗?为什么?
6.(遵义中考)如图,∠1+∠2=180°,∠3=104°,则∠4的度数是( )
A.74° B.76° C.84° D.86°
B
7.(聊城中考)如图,直线AB∥EF,C是直线AB上一点,D是直线AB外一点,若∠BCD=95°,∠CDE=25°,则∠DEF的度数是( )
A.110° B.115° C.120° D.125°
C
8.如图,∠BDE=∠EBD,要使AB∥DE,应添加的一个条件是________________________________.(填一个即可)
∠ABD=∠EBD(答案不唯一)
9.如图,∠AEF+∠CFE=180°,∠1=∠2,EG与HF平行吗?为什么?
解:平行.
理由:∵∠AEF+∠CFE=180°,∴AB∥CD.∴∠AEF=∠EFD.∵∠1=∠2,∴∠AEF-∠1=∠EFD-∠2,即∠GEF=∠HFE.∴EG∥HF
10.如图,AE⊥BC,FG⊥BC,∠1=∠2,∠D=∠3+60°,∠CBD=70°.
(1)求证:AB∥CD;
(2)求∠BCD的度数.
解:(1)证明:∵AE⊥BC,FG⊥BC,∴AE∥GF.∴∠2=∠EAB.∵∠1=∠2,∴∠1=∠EAB.∴AB∥CD
(2)∵AB∥CD,∴∠D+∠CBD+∠3=180°.
∵∠D=∠3+60°,∠CBD=70°,∴∠3=25°.又∵AB∥CD,∴∠BCD=∠3=25°
11.如图,已知:点A,B,C在一条直线上.
(1)请从三个论断:①AD∥BE;②∠1=∠2;③∠A=∠E中,选两个作为条件,另一个作为结论构成一个真命题:
条件:___________________________.
结论:________________________;
①AD∥BE;②∠1=∠2
③∠A=∠E
(2)证明你所构建的是真命题.
证明:∵AD∥BE,∴∠A=∠EBC,
∵∠1=∠2,∴DE∥BC,
∴∠E=∠EBC,∴∠A=∠E
再见
人教版 · 数学· 七年级(下)
第5章 相交线与平行线
5.2.1 平行线
1.了解两条直线的平行关系,掌握有关的符号表示。
2.学会用三角尺、量角器画平行线。
3.掌握平行公理及其推论,培养空间想象能力。
学习目标
如图,分别将木条a、b与木条c钉在一起,并把它们想象成在同一平面内两端可以无限延伸的三条直线.转动a,直线a从在c的左侧与直线b相交逐步变为在c的右侧与b相交.想象一下,在这个过程中,有没有直线a与直线b不相交的位置呢?
a
b
c
a
b
c
a
b
c
新知一 平行线的定义及表示
合作探究
在木条转动过程中,存在一个直线a与直线b不相交的位置,这时我们说直线a与b互相平行.
平行线在生活中是很常见的,你还能举出其他一些例子吗?
在木条转动过程中,存在直线a与直线b不相交的情形,这时我们说直线a与b互相平行.记作“a∥b”.
在同一平面内,不相交的两条直线叫做平行线.
注意:平行线的定义包含三层意思:
(1)“在同一平面内”是前提条件;
(2)“不相交”就是说两条直线没有交点;
(3)平行线指的是“两条直线”而不是两条射线或两条线段.
平行线的概念
a
b
c
我们通常用“//”表示平行.
C
B
A
D
a ∥ b
AB ∥ CD
a
b
读作:“AB 平行于 CD”
读作:“a平行于b ”
平行线的表示法:
同一平面内两直线的位置关系:
平行
相交
垂直
相交但不垂直
a
b
a⊥b
a ∥b
a
b
b
a
在同一平面内,不重合的两直线的位置关系只有平行与相交两种.
例 下列说法正确的是( )
A.两条不相交的直线一定相互平行
B.在同一平面内,两条不平行的直线一定相交
C.在同一平面内,两条不相交的线段一定平行
D.在同一平面内,两条不相交的射线互相平行
B
典例精析 平行线的识别
下列说法中,正确的个数有( )
(1)在同一平面内不相交的两条线段必平行
(2)在同一平面内不相交的两条直线必平行
(3)在同一平面内不平行的两条线段必相交
(4)在同一平面内不平行的两条直线必相交
A.1个 B.2个 C.3个 D.4个
B
√
×
×
√
巩固新知
一、放
二、靠
三、推
四、画
B
A
新知二 平行线的画法
“推平行线法”:
合作探究
●
一放
二靠
三推
四画
怎样画平行线?动手画一画吧!
这种方法你会了吗?
已知直线AB和直线外一点P,过点P画一条直线和已知直线AB平行.
P
B
A
A
B
P
例 如图,在△ ABC中,P是AC边上一点.过点P画AB的平行线.
C
D
解:如图所示:
典例精析 按要求作出平行线
PD就是所要画的直线.
A
B
P
如图,在△ABC 中,P是AC边上一点.过点P画BC的平行线.
C
E
解:PE就是所要画的直线.
巩固新知
·
A
·
B
(3)经过点C能画出几条直线与直线AB平行?
(4)过点D画一条直线与直线AB平行,与(3)中所画的直线平行吗?
·
·
C
D
(1)经过点C能画出几条直线?
无数条.
1条.
a
b
(2)与直线AB平行的直线有几条?
无数条.
平行.
你能对这些情况进行归纳总结吗?
新知三 平行公理及其推论
合作探究
平行公理:经过直线外一点,有且只有一条直线与这条
直线平行.
·
A
·
B
·
·
C
D
温馨提示:
(1)平行公理中强调“直线外一点”,若点在直线上,不可能有平行线;
(2)“有且只有”强调这样的直线是存在的,也是唯一的.
几何语言:
c
b
a
平行公理的推论(平行线的传递性):
如果两条直线都与第三条直线平行,那么这两条直线也互相平行.
∵a//c , c//b,
∴ a//b(如果两条直线都和第三条直线平行,那么这两条直线也互相平行).
例 下列说法中,正确的是( )
(1)过一点,有且只有一条直线与已知直线平行;
(2)平行于同一条直线的两条直线互相平行;
(3)一条直线的平行线有且只有一条;
(4)若a∥b,b∥c,则a∥c.
A.(1)(2) B.(2)(3)
C.(1)(3) D.(2)(4)
典例精析 平行公理及其推论的应用
D
×
√
×
√
若AB∥CD,AB∥EF,则__________. 如图所示,MC∥AB,NC∥AB,则点M,C,N在同一条直线上,理由是___________________________________________________
CD∥EF
经过直线外一点,有且只有一条直线与这条直线平行.
巩固新知
1.(4分)下列说法正确的是( )
A.同一平面内,没有公共点的两条线段是平行线
B.同一平面内,两条平行线只有一个公共点
C.同一平面内,没有公共点的两条直线是平行线
D.两条不相交的直线叫做平行线
C
课堂练习
2.(5分)同一平面内,直线AB与直线CD满足下列条件,指出其对应的位置关系.
(1)若直线AB与直线CD没有公共点,则直线AB与直线CD的位置关系为________;
(2)直线AB与直线CD有且只有一个公共点,则直线AB与直线CD的位置关系为__________.
平行
相交
3.(5分)在同一平面内,下列说法中,错误的是( )
A.过两点有且只有一条直线
B.过一点有无数条直线与已知直线平行
C.过直线外一点有且有一条直线与已知直线平行
D.过一点有且只有一条直线与已知直线垂直
B
4.(5分)如图,PC∥AB,QC∥AB,则点P,C,Q在一条直线上,理由是__________________________________________________.
经过直线外一点,有且只有一条直线与这条直线平行
5.(8分)如图,P,Q分别是直线EF外两点.
(1)过点P画直线AB∥EF,过点Q画直线CD∥EF;
(2)AB与CD有怎样的位置关系?为什么?
解:(1)如图
(2)AB∥CD
理由:因为AB∥EF,CD∥EF,
所以AB∥CD
6.(10分)如图所示,取一张长方形的硬纸板ABCD,将硬纸板ABCD对折使CD与AB重合,EF为折痕.把长方形ABFE平放在桌面上,另一个面CDEF无论怎么改变位置总有CD∥AB存在,你知道为什么吗?
解:因为AB∥EF,CD∥EF,所以CD∥AB
【综合运用】
7.(12分)如图,两条直线l1与l2可以把一个平面分成3部分(如图①),也可以把一个平面分成4部分(如图②),若平面内有三条直线,可以把平面分成多少部分?(本题只考虑在同一平面内的情况)
解:可以把平面分成4部分或7部分或6部分,如图
1.在同一平面内,不相交的两条直线叫做平行线.
3.如果两条直线都与第三条直线平行,那么这两条直
线互相平行.
2.经过直线外一点,有且只有一条直线与已知直线平行.
平行公理的推论
平行公理
定义
归纳新知
1.如图,直线AC和直线BD相交于点O,OE平分∠BOC.若∠1+∠2=80°,则∠3的度数为( )
A.40° B.50° C.60° D.70°
D
课后练习
2.如图所示,下列结论中不正确的是( )
A.∠1和∠2是同位角 B.∠2和∠3是同旁内角
C.∠1和∠4是同位角 D.∠2和∠4是内错角
A
3.以下两条直线互相垂直的是( )
①两条直线相交所成的四个角中有一个是直角;②两条直线相交所成的所有邻补角都相等;③两条直线相交,有一组邻补角相等;④两条直线相交,对顶角互补.
A.①③ B.①②③
C.②③④ D.①②③④
D
4.(杭州中考)若线段AM,AN分别是△ABC的BC边上的高线和中线,
则( )
A.AM>AN B.AM≥AN
C.AM<AN D.AM≤AN
D
5.如图,直线AB与CD相交于点O,OP是∠BOC的平分线,OE⊥AB,OF⊥CD.
(1)若∠AOD=50°,请求出∠DOP的度数;
(2)OP平分∠EOF吗?为什么?
6.(遵义中考)如图,∠1+∠2=180°,∠3=104°,则∠4的度数是( )
A.74° B.76° C.84° D.86°
B
7.(聊城中考)如图,直线AB∥EF,C是直线AB上一点,D是直线AB外一点,若∠BCD=95°,∠CDE=25°,则∠DEF的度数是( )
A.110° B.115° C.120° D.125°
C
8.如图,∠BDE=∠EBD,要使AB∥DE,应添加的一个条件是________________________________.(填一个即可)
∠ABD=∠EBD(答案不唯一)
9.如图,∠AEF+∠CFE=180°,∠1=∠2,EG与HF平行吗?为什么?
解:平行.
理由:∵∠AEF+∠CFE=180°,∴AB∥CD.∴∠AEF=∠EFD.∵∠1=∠2,∴∠AEF-∠1=∠EFD-∠2,即∠GEF=∠HFE.∴EG∥HF
10.如图,AE⊥BC,FG⊥BC,∠1=∠2,∠D=∠3+60°,∠CBD=70°.
(1)求证:AB∥CD;
(2)求∠BCD的度数.
解:(1)证明:∵AE⊥BC,FG⊥BC,∴AE∥GF.∴∠2=∠EAB.∵∠1=∠2,∴∠1=∠EAB.∴AB∥CD
(2)∵AB∥CD,∴∠D+∠CBD+∠3=180°.
∵∠D=∠3+60°,∠CBD=70°,∴∠3=25°.又∵AB∥CD,∴∠BCD=∠3=25°
11.如图,已知:点A,B,C在一条直线上.
(1)请从三个论断:①AD∥BE;②∠1=∠2;③∠A=∠E中,选两个作为条件,另一个作为结论构成一个真命题:
条件:___________________________.
结论:________________________;
①AD∥BE;②∠1=∠2
③∠A=∠E
(2)证明你所构建的是真命题.
证明:∵AD∥BE,∴∠A=∠EBC,
∵∠1=∠2,∴DE∥BC,
∴∠E=∠EBC,∴∠A=∠E
再见
