初中数学人教版七年级下册5.2.1平行线习题课件(共31张PPT)
文档属性
| 名称 | 初中数学人教版七年级下册5.2.1平行线习题课件(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 390.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-31 14:56:10 | ||
图片预览







文档简介
(共31张PPT)
第五章 相交线与平行线
第4课时 平行线
目录
01
名师导学
02
课堂讲练
03
分层训练
名师导学
A. 平行线:在同一平面内,__________________________
叫做平行线.
1. 下列说法正确的是( )
A. 两点之间,直线最短
B. 永不相交的两条直线叫做平行线
C. 若AC=BC,则点C为线段AB的中点
D. 两点确定一条直线
不重合且不相交的两条直线
D
B. 平行公理:经过直线外一点,有且只有一条直线与这条直线平行.
推论:如果两条直线都与第三条直线______________,那么这两条直线也互相______________.
用数学符号表示为:如果b∥a,c∥a,那么_____________.
平行
平行
b∥c
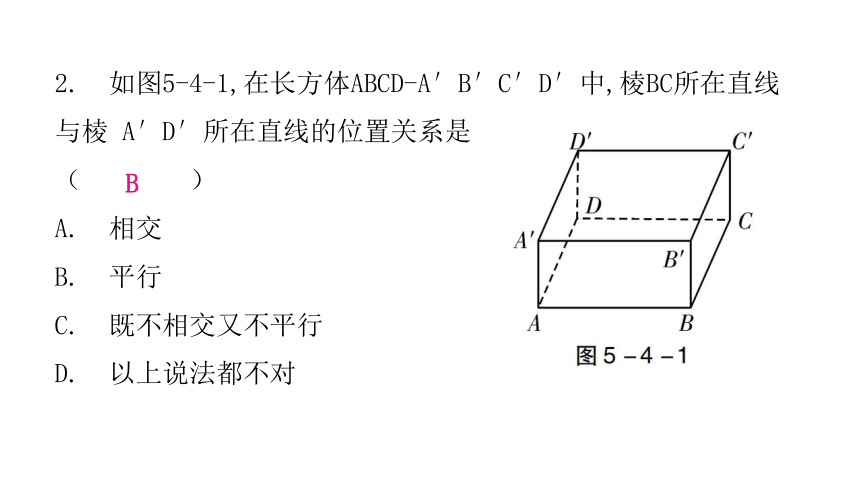
2. 如图5-4-1,在长方体ABCD-A′B′C′D′中,棱BC所在直线与棱 A′D′所在直线的位置关系是
( )
A. 相交
B. 平行
C. 既不相交又不平行
D. 以上说法都不对
B
课堂讲练
典型例题
知识点1:平行线的概念
B
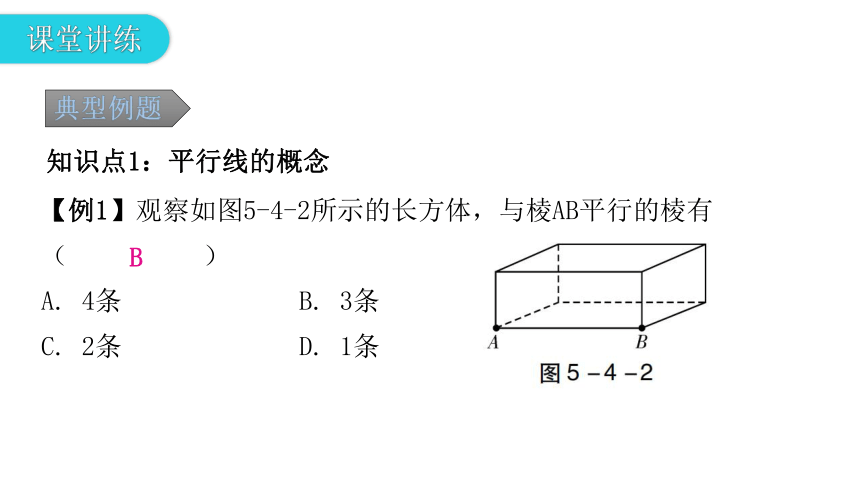
【例1】观察如图5-4-2所示的长方体,与棱AB平行的棱有
( )
A. 4条 B. 3条
C. 2条 D. 1条
思路点拨:熟记平行线的定义,即同一平面内,不重合且不相交的两条直线叫做平行线.
举一反三
1. 在同一平面内,两条不重合直线的位置关系只可能是
( )
A. 垂直或平行
B. 垂直或相交
C. 平行或相交
D. 平行、垂直或相交
C
典型例题
知识点2:平行线的画法
【例2】如图5-4-3,直线MN,PQ交于点O,R为MN,PQ外一点,过点R画直线AB∥PQ,直线CD∥MN.
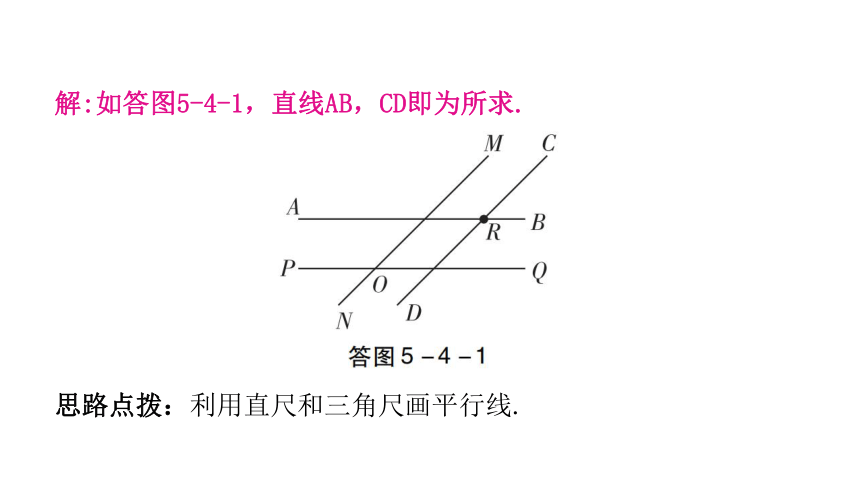
解:如答图5-4-1,直线AB,CD即为所求.
思路点拨:利用直尺和三角尺画平行线.
举一反三
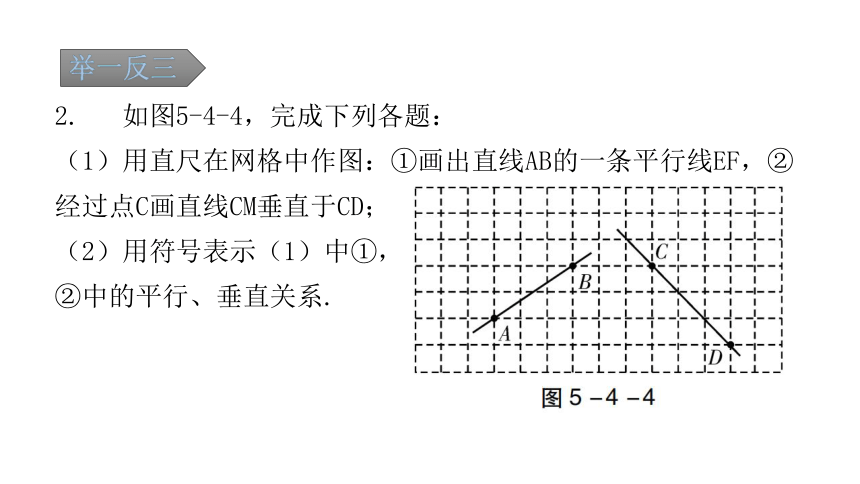
2. 如图5-4-4,完成下列各题:
(1)用直尺在网格中作图:①画出直线AB的一条平行线EF,②经过点C画直线CM垂直于CD;
(2)用符号表示(1)中①,
②中的平行、垂直关系.
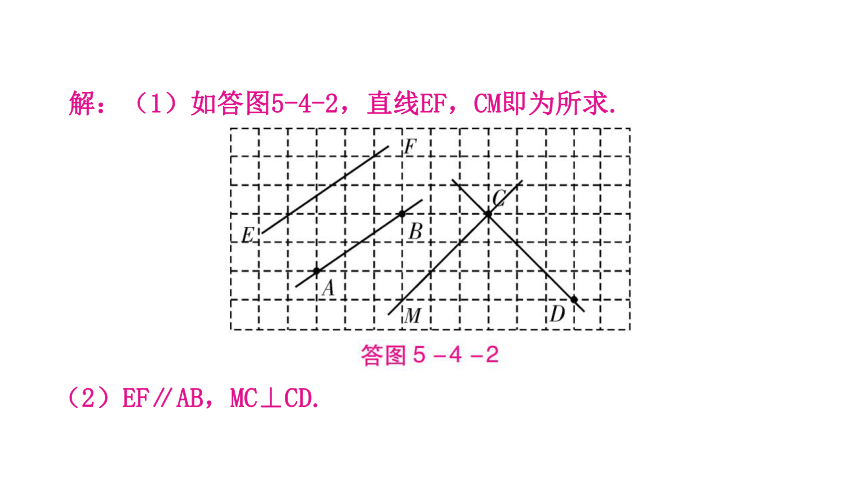
解:(1)如答图5-4-2,直线EF,CM即为所求.
(2)EF∥AB,MC⊥CD.
典型例题
知识点3:平行公理及其推论
【例3】如图5-4-5,直线a∥b,b∥c,直线d与a相交于点A.
(1)判断a与c的位置关系,并说明理由;
(2)判断c与d的位置关系,并说明理由.
解:(1)a与c的位置关系是a∥c.
理由如下:
因为直线a∥b,b∥c,
所以a∥c.
(2)c与d的位置关系是相交. 理由如下:
因为c∥a,直线d与a相交于点A,
所以c与d的位置关系是相交.
思路点拨:如果b∥a,c∥a,那么b∥c.
举一反三
3. 如图5-4-6,已知OA∥CD,OB∥CD,那么∠AOB是平角,为什么?
解:因为OA∥CD,OB∥CD且OA,OB交于点O,
根据过直线CD外一点O有且只有一条直线与已知直线CD平行,
所以OA,OB共直线.
所以点A,O,B共直线,即∠AOB是平角.
分层训练
A组
1. 两条线段平行是指( )
A. 两条线段所在直线平行
B. 两条线段都在同一直线上且方向相同
C. 两条线段方向相反
D. 两条线段都是水平的
A
2. a,b,c为同一平面内任意三条直线,则它们的交点可能有
( )
A. 1个或2个或3个
B. 0个或1个或2个或3个
C. 1个或2个
D. 以上都不对
B
3. 下列说法:①相等的角是对顶角; ②同位角相等; ③过一点有且只有一条直线与已知直线平行; ④直线外一点到这条直线的垂线段的长度,叫做点到直线的距离. 其中正确的有
( )
A. 0个 B. 1个
C. 2个 D. 3个
B
4. 如图5-4-7,能相交的是__________,平行的是__________. (填序号)
③
⑤
5. 在同一平面内,直线l1与l2满足下列条件,写出其对应的位置关系.
(1)l1与l2没有公共点,则l1与l2______________;
(2)l1与l2有且只有一个公共点,则l1与l2______________;
(3)l1与l2有两个公共点,则l1与l2______________.
平行
相交
重合
6. 按要求作图:直线AB,CD是相交直线,点P是直线AB,CD外一点,直线EF经过点P,且与直线AB平行,与直线CD相交于点E.
解:如答图5-4-3.
答图5-4-3
7. 已知在同一平面内,直线a∥b,b∥c,c∥d,则a与d的关系是什么,为什么?
解:a∥d.
理由如下:
因为a∥b,b∥c,
所以a∥c.
因为c∥d,
所以a∥d.
B组
8. 下列各种说法中,错误的是______________. (填序号)
①过一点有且只有一条直线与已知直线平行;
②在同一平面内,两条不相交的线段是平行线段;
③两条直线没有交点,则这两条直线平行;
④在同一平面内,若直线AB∥CD,直线AB与EF相交,则CD与EF相交.
①②③
9. 如图5-4-8,已知直线a,点B,点C.
(1)过点B画直线a的平行线,能画几条?
(2)过点C画直线a的平行线,它与过点B的平行线平行吗?
解:(1)如答图5-4-4,过直线a外的一点B画直线a的平行线,只能画一条直线与直线a平行.
(2)如答图5-4-4,过点C画直线a的平行线,它与过点B的平行线平行. 理由如下:
因为b∥a,c∥a,
所以c∥b.
C组
10. 如图5-4-9,建筑工人要检验墙壁是否竖直,可先在一条狭长的木板上画一条直线a,使其平行于木板的一边,再在直线a的上端O处钉一只钉子,挂一条铅垂线OP,最后把木板的一边紧贴墙壁,这时如果OP能与直线a重合,那么墙壁便是竖直的. 你能说出为什么吗
解:因为经过直线外一点,有且只有一条直线与这条直线平行,现在直线a与墙壁平行,若a和OP重合,则说明墙壁是竖直的,否则说明墙壁不是竖直的.
11. (1)补全如图5-4-10所示的图形,使之成为长方体ABCD-EFGH的直观图,并标出顶点的字母;
(2)图中与棱AB平行的棱有_____________________;
CD,EF,GH
(3)图中棱CG和面ABFE的位置关系是______________.
平行
解:(1)如答图5-4-5所示即为补全的图形.
第五章 相交线与平行线
第4课时 平行线
目录
01
名师导学
02
课堂讲练
03
分层训练
名师导学
A. 平行线:在同一平面内,__________________________
叫做平行线.
1. 下列说法正确的是( )
A. 两点之间,直线最短
B. 永不相交的两条直线叫做平行线
C. 若AC=BC,则点C为线段AB的中点
D. 两点确定一条直线
不重合且不相交的两条直线
D
B. 平行公理:经过直线外一点,有且只有一条直线与这条直线平行.
推论:如果两条直线都与第三条直线______________,那么这两条直线也互相______________.
用数学符号表示为:如果b∥a,c∥a,那么_____________.
平行
平行
b∥c
2. 如图5-4-1,在长方体ABCD-A′B′C′D′中,棱BC所在直线与棱 A′D′所在直线的位置关系是
( )
A. 相交
B. 平行
C. 既不相交又不平行
D. 以上说法都不对
B
课堂讲练
典型例题
知识点1:平行线的概念
B
【例1】观察如图5-4-2所示的长方体,与棱AB平行的棱有
( )
A. 4条 B. 3条
C. 2条 D. 1条
思路点拨:熟记平行线的定义,即同一平面内,不重合且不相交的两条直线叫做平行线.
举一反三
1. 在同一平面内,两条不重合直线的位置关系只可能是
( )
A. 垂直或平行
B. 垂直或相交
C. 平行或相交
D. 平行、垂直或相交
C
典型例题
知识点2:平行线的画法
【例2】如图5-4-3,直线MN,PQ交于点O,R为MN,PQ外一点,过点R画直线AB∥PQ,直线CD∥MN.
解:如答图5-4-1,直线AB,CD即为所求.
思路点拨:利用直尺和三角尺画平行线.
举一反三
2. 如图5-4-4,完成下列各题:
(1)用直尺在网格中作图:①画出直线AB的一条平行线EF,②经过点C画直线CM垂直于CD;
(2)用符号表示(1)中①,
②中的平行、垂直关系.
解:(1)如答图5-4-2,直线EF,CM即为所求.
(2)EF∥AB,MC⊥CD.
典型例题
知识点3:平行公理及其推论
【例3】如图5-4-5,直线a∥b,b∥c,直线d与a相交于点A.
(1)判断a与c的位置关系,并说明理由;
(2)判断c与d的位置关系,并说明理由.
解:(1)a与c的位置关系是a∥c.
理由如下:
因为直线a∥b,b∥c,
所以a∥c.
(2)c与d的位置关系是相交. 理由如下:
因为c∥a,直线d与a相交于点A,
所以c与d的位置关系是相交.
思路点拨:如果b∥a,c∥a,那么b∥c.
举一反三
3. 如图5-4-6,已知OA∥CD,OB∥CD,那么∠AOB是平角,为什么?
解:因为OA∥CD,OB∥CD且OA,OB交于点O,
根据过直线CD外一点O有且只有一条直线与已知直线CD平行,
所以OA,OB共直线.
所以点A,O,B共直线,即∠AOB是平角.
分层训练
A组
1. 两条线段平行是指( )
A. 两条线段所在直线平行
B. 两条线段都在同一直线上且方向相同
C. 两条线段方向相反
D. 两条线段都是水平的
A
2. a,b,c为同一平面内任意三条直线,则它们的交点可能有
( )
A. 1个或2个或3个
B. 0个或1个或2个或3个
C. 1个或2个
D. 以上都不对
B
3. 下列说法:①相等的角是对顶角; ②同位角相等; ③过一点有且只有一条直线与已知直线平行; ④直线外一点到这条直线的垂线段的长度,叫做点到直线的距离. 其中正确的有
( )
A. 0个 B. 1个
C. 2个 D. 3个
B
4. 如图5-4-7,能相交的是__________,平行的是__________. (填序号)
③
⑤
5. 在同一平面内,直线l1与l2满足下列条件,写出其对应的位置关系.
(1)l1与l2没有公共点,则l1与l2______________;
(2)l1与l2有且只有一个公共点,则l1与l2______________;
(3)l1与l2有两个公共点,则l1与l2______________.
平行
相交
重合
6. 按要求作图:直线AB,CD是相交直线,点P是直线AB,CD外一点,直线EF经过点P,且与直线AB平行,与直线CD相交于点E.
解:如答图5-4-3.
答图5-4-3
7. 已知在同一平面内,直线a∥b,b∥c,c∥d,则a与d的关系是什么,为什么?
解:a∥d.
理由如下:
因为a∥b,b∥c,
所以a∥c.
因为c∥d,
所以a∥d.
B组
8. 下列各种说法中,错误的是______________. (填序号)
①过一点有且只有一条直线与已知直线平行;
②在同一平面内,两条不相交的线段是平行线段;
③两条直线没有交点,则这两条直线平行;
④在同一平面内,若直线AB∥CD,直线AB与EF相交,则CD与EF相交.
①②③
9. 如图5-4-8,已知直线a,点B,点C.
(1)过点B画直线a的平行线,能画几条?
(2)过点C画直线a的平行线,它与过点B的平行线平行吗?
解:(1)如答图5-4-4,过直线a外的一点B画直线a的平行线,只能画一条直线与直线a平行.
(2)如答图5-4-4,过点C画直线a的平行线,它与过点B的平行线平行. 理由如下:
因为b∥a,c∥a,
所以c∥b.
C组
10. 如图5-4-9,建筑工人要检验墙壁是否竖直,可先在一条狭长的木板上画一条直线a,使其平行于木板的一边,再在直线a的上端O处钉一只钉子,挂一条铅垂线OP,最后把木板的一边紧贴墙壁,这时如果OP能与直线a重合,那么墙壁便是竖直的. 你能说出为什么吗
解:因为经过直线外一点,有且只有一条直线与这条直线平行,现在直线a与墙壁平行,若a和OP重合,则说明墙壁是竖直的,否则说明墙壁不是竖直的.
11. (1)补全如图5-4-10所示的图形,使之成为长方体ABCD-EFGH的直观图,并标出顶点的字母;
(2)图中与棱AB平行的棱有_____________________;
CD,EF,GH
(3)图中棱CG和面ABFE的位置关系是______________.
平行
解:(1)如答图5-4-5所示即为补全的图形.
