人教版数学七年级下册5.2.1平行线课件(共24张PPT)
文档属性
| 名称 | 人教版数学七年级下册5.2.1平行线课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-31 15:11:55 | ||
图片预览




文档简介
(共24张PPT)
平行线
问题 前面我们学的两条直线具有怎样位置关系?
两条直线相交(其中垂直是相交的特殊情形)
生活中两条直线除了相交以外,还有什么情形呢?
下面我们一起来体会一下.
新知引入
国旗知多少
古巴国旗
俄罗斯国旗
比利时国旗
荷兰国旗
阿根廷国旗
瑞士国旗
新知引入
生活中的平行线
新知引入
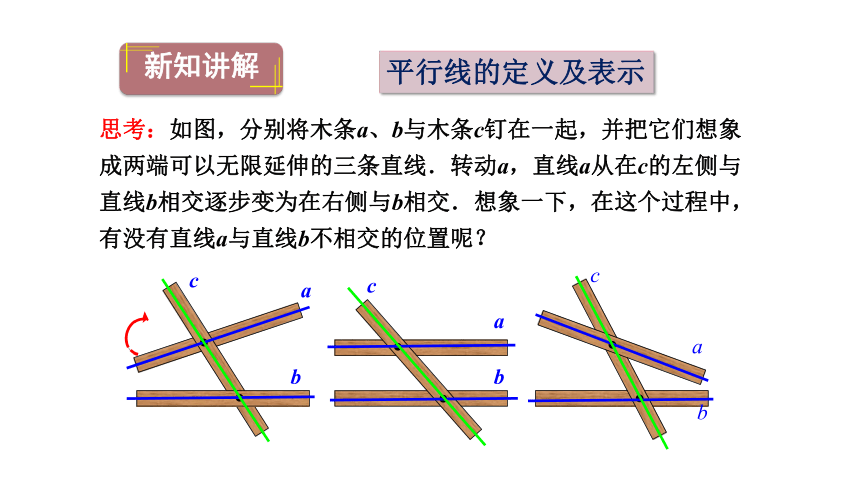
思考:如图,分别将木条a、b与木条c钉在一起,并把它们想象成两端可以无限延伸的三条直线.转动a,直线a从在c的左侧与直线b相交逐步变为在右侧与b相交.想象一下,在这个过程中,有没有直线a与直线b不相交的位置呢?
a
b
c
a
b
c
a
b
c
平行线的定义及表示
新知讲解
在木条转动过程中,存在一条直线a与直线b不相交的情形,这时我们说直线a与b互相平行.记作“a∥b”.
在同一平面内,不相交的两条直线叫做平行线.
注意:平行线的定义包含三层意思:
①“在同一平面内”是前提条件;
②“不相交”就是说两条直线没有交点;
③平行线指的是“两条直线”而不是两条射线或两条线段.
一、平行线的概念
a
b
c
新知讲解
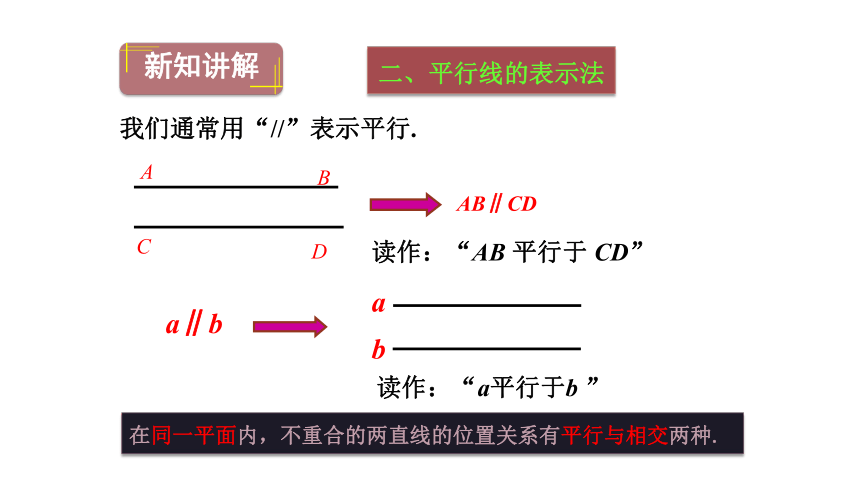
我们通常用“//”表示平行.
C
B
A
D
a∥b
AB∥CD
a
b
读作:“AB 平行于 CD”
读作:“a平行于b ”
在同一平面内,不重合的两直线的位置关系有平行与相交两种.
二、平行线的表示法
新知讲解
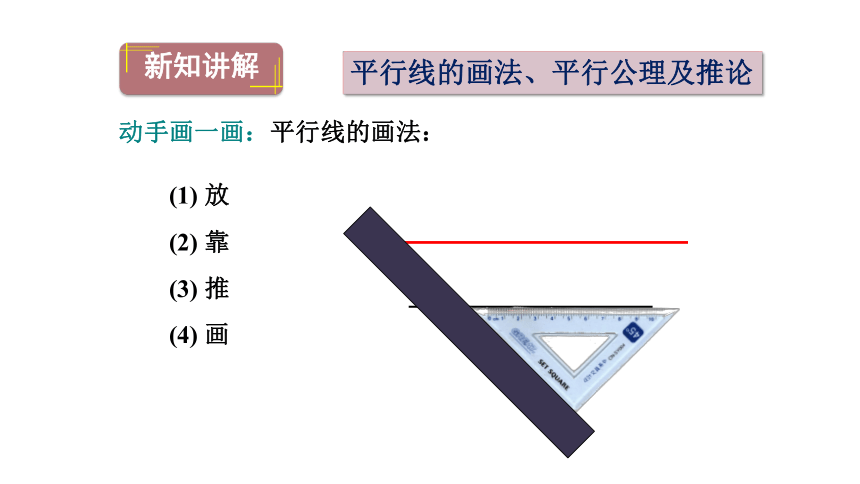
动手画一画:平行线的画法:
(1) 放
(2) 靠
(3) 推
(4) 画
平行线的画法、平行公理及推论
新知讲解
·
A
·
B
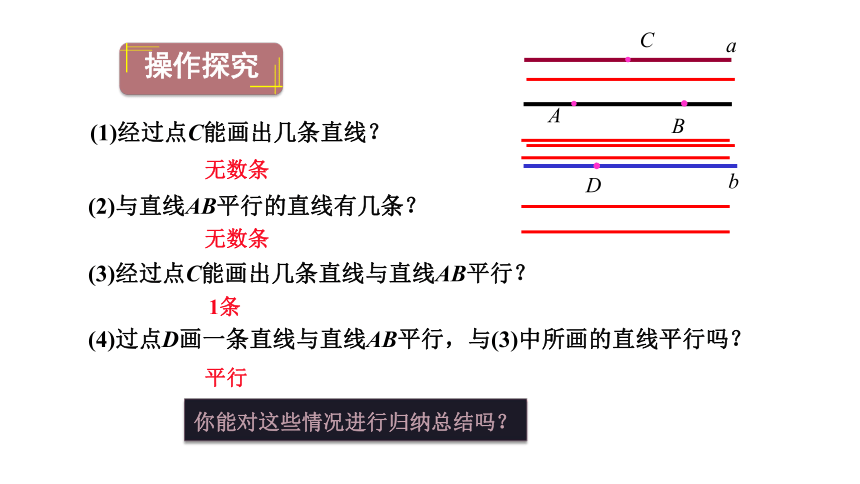
(3)经过点C能画出几条直线与直线AB平行?
(4)过点D画一条直线与直线AB平行,与(3)中所画的直线平行吗?
·
·
C
D
(1)经过点C能画出几条直线?
无数条
1条
a
b
(2)与直线AB平行的直线有几条?
无数条
平行
你能对这些情况进行归纳总结吗?
操作探究
平行公理:经过直线外一点,有且只有一条直线
与已知直线平行.
三、平行公理
·
A
·
B
·
·
C
D
a
b
新知讲解
几何语言表达:
c
b
a
如果两条直线都与第三条直线平行,那么这两条直线互相平行.
∵a//c,c//b(已知)
∴a//b.
新知讲解
四、平行公理的推论
例1.下列说法正确的是( )
A.在同一平面内,不相交的两条射线是平行线;
B.在同一平面内,不相交的两条线段是平行线;
C.在同一平面内,两条不重合的直线的位置关系不是
相交就是平行;
D.不相交的两条直线是平行线
C
新知应用
点名
例2.下列说法正确的是( )
A.一条直线的平行线有且只有一条
B.经过一点有且只有一条直线与已知直线平行
C.经过一点有两条直线与某一直线平行
D.过直线外一点有且只有一条直线与已知直线平行
D
新知应用
点名
例3.下列推理正确的是( )
A.因为a // d,b // c,所以c // d
B.因为a // c,b // d,所以c // d
C.因为a // b,a // c,所以b // c
D.因为a // b,c // d,所以a // c
C
新知应用
抢答
例4.完成下列推理,并在括号内注明理由.
①如图,因为AB//DE,BC//DE(已知),所以A,B,C三点 .
( )
·
·
·
A
D
E
B
C
在同一直线上
经过直线外一点有且只有一条直线与这条直线平行
新知应用
②如图,因为AB//CD,CD//EF(已知),
所以________ //_________.
(
)
C
A
B
D
E
F
AB
EF
如果两条直线都和第三条直线平行,那么这两条直线也互相平行
新知应用
变式1.一条直线与另两条平行线的关系是( )
新知演练
A.一定与另两条直线平行
B.与其中一条平行,另一条相交
C.一定都相交
D.与两条平行线都平行或都相交
D
抢答
②a与b有且只有一个公共点,则a与b ;
新知演练
变式2.在同一平面内,直线a与b满足下列条件,把它们的位置关系填在后面的横线上.
①a与b没有公共点,则a与b ;
平行
相交
重合
③a与b有两个公共点,则a与b .
点名
巩固练习
1.如图,在长方体中,与棱AD平行的棱共有 条.
解析
∵AD∥A1D1∥B1C1∥BC,
∴与棱AD平行的棱有3条.
3
检测
①过A点作AE∥BC,交 于点E ;
④过D点作DH∥BC,交 于点H ;
③过C点作CG∥AD,交AB的 于点G ;
新知演练
2.如图,根据要求填空.
DC
延长线
BA的延长线
②过B点作BF∥AD,交 于点F ;
A
B
C
D
E
F
G
H
DC
拍照
巩固练习
3.如图,在同一平面内,若AB∥CD,EF与AB相交于点P,EF能与CD平行吗?为什么?
答:假设EF∥CD,
又因为AB∥CD,
根据平行于同一条直线的两条直线平行,
有AB∥EF.
这与AB和EF相交于P点矛盾,
所以EF与CD不平行.
巩固练习
4.将一张长方形的硬纸片ABCD对折后打开,折痕为EF,把长方形ABEF平摊在桌面上,另一面CDFE无论怎样改变位置,总有CD∥AB存在,为什么?
A
E
B
C
D
F
答:因为CD∥EF,EF∥AB
所以CD∥AB
即如果两条直线都和第三条直线平行,
那么这两条直线也互相平行.
拓展提升
在同一平面内,任意三条直线有哪几种不同的位置关系?你能画图说明吗?
答:如上图所示,共有四种位置关系.
C
A
B
D
E
F
①
C
A
B
D
E
F
②
C
A
B
D
E
F
③
C
A
B
D
E
F
④
1.在同一平面内,不相交的两条直线叫做平行线.
3.如果两条直线都与第三条直线平行,那么这两条直线互相平行.
2.经过直线外一点,有且只有一条直线与已知直线平行.
课堂总结
平行线
问题 前面我们学的两条直线具有怎样位置关系?
两条直线相交(其中垂直是相交的特殊情形)
生活中两条直线除了相交以外,还有什么情形呢?
下面我们一起来体会一下.
新知引入
国旗知多少
古巴国旗
俄罗斯国旗
比利时国旗
荷兰国旗
阿根廷国旗
瑞士国旗
新知引入
生活中的平行线
新知引入
思考:如图,分别将木条a、b与木条c钉在一起,并把它们想象成两端可以无限延伸的三条直线.转动a,直线a从在c的左侧与直线b相交逐步变为在右侧与b相交.想象一下,在这个过程中,有没有直线a与直线b不相交的位置呢?
a
b
c
a
b
c
a
b
c
平行线的定义及表示
新知讲解
在木条转动过程中,存在一条直线a与直线b不相交的情形,这时我们说直线a与b互相平行.记作“a∥b”.
在同一平面内,不相交的两条直线叫做平行线.
注意:平行线的定义包含三层意思:
①“在同一平面内”是前提条件;
②“不相交”就是说两条直线没有交点;
③平行线指的是“两条直线”而不是两条射线或两条线段.
一、平行线的概念
a
b
c
新知讲解
我们通常用“//”表示平行.
C
B
A
D
a∥b
AB∥CD
a
b
读作:“AB 平行于 CD”
读作:“a平行于b ”
在同一平面内,不重合的两直线的位置关系有平行与相交两种.
二、平行线的表示法
新知讲解
动手画一画:平行线的画法:
(1) 放
(2) 靠
(3) 推
(4) 画
平行线的画法、平行公理及推论
新知讲解
·
A
·
B
(3)经过点C能画出几条直线与直线AB平行?
(4)过点D画一条直线与直线AB平行,与(3)中所画的直线平行吗?
·
·
C
D
(1)经过点C能画出几条直线?
无数条
1条
a
b
(2)与直线AB平行的直线有几条?
无数条
平行
你能对这些情况进行归纳总结吗?
操作探究
平行公理:经过直线外一点,有且只有一条直线
与已知直线平行.
三、平行公理
·
A
·
B
·
·
C
D
a
b
新知讲解
几何语言表达:
c
b
a
如果两条直线都与第三条直线平行,那么这两条直线互相平行.
∵a//c,c//b(已知)
∴a//b.
新知讲解
四、平行公理的推论
例1.下列说法正确的是( )
A.在同一平面内,不相交的两条射线是平行线;
B.在同一平面内,不相交的两条线段是平行线;
C.在同一平面内,两条不重合的直线的位置关系不是
相交就是平行;
D.不相交的两条直线是平行线
C
新知应用
点名
例2.下列说法正确的是( )
A.一条直线的平行线有且只有一条
B.经过一点有且只有一条直线与已知直线平行
C.经过一点有两条直线与某一直线平行
D.过直线外一点有且只有一条直线与已知直线平行
D
新知应用
点名
例3.下列推理正确的是( )
A.因为a // d,b // c,所以c // d
B.因为a // c,b // d,所以c // d
C.因为a // b,a // c,所以b // c
D.因为a // b,c // d,所以a // c
C
新知应用
抢答
例4.完成下列推理,并在括号内注明理由.
①如图,因为AB//DE,BC//DE(已知),所以A,B,C三点 .
( )
·
·
·
A
D
E
B
C
在同一直线上
经过直线外一点有且只有一条直线与这条直线平行
新知应用
②如图,因为AB//CD,CD//EF(已知),
所以________ //_________.
(
)
C
A
B
D
E
F
AB
EF
如果两条直线都和第三条直线平行,那么这两条直线也互相平行
新知应用
变式1.一条直线与另两条平行线的关系是( )
新知演练
A.一定与另两条直线平行
B.与其中一条平行,另一条相交
C.一定都相交
D.与两条平行线都平行或都相交
D
抢答
②a与b有且只有一个公共点,则a与b ;
新知演练
变式2.在同一平面内,直线a与b满足下列条件,把它们的位置关系填在后面的横线上.
①a与b没有公共点,则a与b ;
平行
相交
重合
③a与b有两个公共点,则a与b .
点名
巩固练习
1.如图,在长方体中,与棱AD平行的棱共有 条.
解析
∵AD∥A1D1∥B1C1∥BC,
∴与棱AD平行的棱有3条.
3
检测
①过A点作AE∥BC,交 于点E ;
④过D点作DH∥BC,交 于点H ;
③过C点作CG∥AD,交AB的 于点G ;
新知演练
2.如图,根据要求填空.
DC
延长线
BA的延长线
②过B点作BF∥AD,交 于点F ;
A
B
C
D
E
F
G
H
DC
拍照
巩固练习
3.如图,在同一平面内,若AB∥CD,EF与AB相交于点P,EF能与CD平行吗?为什么?
答:假设EF∥CD,
又因为AB∥CD,
根据平行于同一条直线的两条直线平行,
有AB∥EF.
这与AB和EF相交于P点矛盾,
所以EF与CD不平行.
巩固练习
4.将一张长方形的硬纸片ABCD对折后打开,折痕为EF,把长方形ABEF平摊在桌面上,另一面CDFE无论怎样改变位置,总有CD∥AB存在,为什么?
A
E
B
C
D
F
答:因为CD∥EF,EF∥AB
所以CD∥AB
即如果两条直线都和第三条直线平行,
那么这两条直线也互相平行.
拓展提升
在同一平面内,任意三条直线有哪几种不同的位置关系?你能画图说明吗?
答:如上图所示,共有四种位置关系.
C
A
B
D
E
F
①
C
A
B
D
E
F
②
C
A
B
D
E
F
③
C
A
B
D
E
F
④
1.在同一平面内,不相交的两条直线叫做平行线.
3.如果两条直线都与第三条直线平行,那么这两条直线互相平行.
2.经过直线外一点,有且只有一条直线与已知直线平行.
课堂总结
