人教版数学七年级下册第五章5.2.1平行线课件(共57张PPT)
文档属性
| 名称 | 人教版数学七年级下册第五章5.2.1平行线课件(共57张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-31 15:13:11 | ||
图片预览










文档简介
(共57张PPT)
第五章
5.2.1 平行线
人教版数学七年级下册
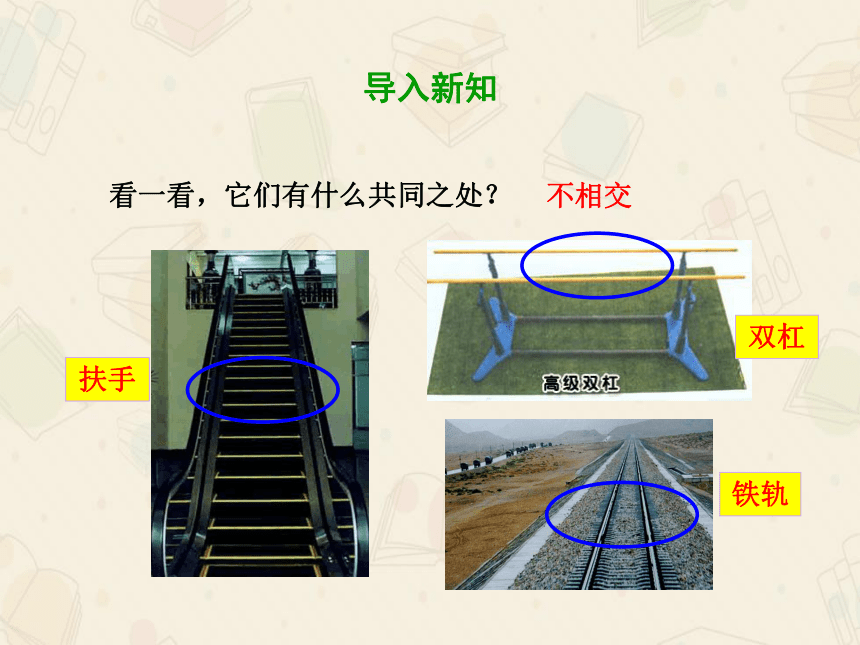
看一看,它们有什么共同之处?
扶手
双杠
铁轨
不相交
导入新知
1.理解平行线的意义,了解同一平面内两条直线的位置关系.
2.理解并掌握平行公理及其推论的内容.
3.会根据几何语句画图,会用直尺和三角板画平行线.
4.了解平行线在实际生活中的应用,能举例加以说明.
学习目标
1
知识点
平行线
什么是平行线?
在同一平面内不相交的两条直线叫做平行线.
在同一平面内、
注意
平行线体现三点:
不相交、
两条直线.
在同一平面内
不相交
两条直线
合作探究
平行在生活中的 应用
如果两根铁轨之间的宽度不相等,又会有什么现象发生?
请你想象,手扶电梯左右扶手之间的宽度如果不相等,会出现什么情况?
教室里能找到平行线吗?
我们通常用“//”表示平行.
平行线的表示:
C
D
B
A
m
n
AB ∥ CD
记作:
m ∥ n
记作:
·
·
·
·
例1 判断下列说法是否正确,并说明理由.
(1)不相交的两条直线是平行线;
(2)在同一平面内,两条不相交的线段是平行线.
导引:(1)没有强调两条直线在同一平面内;
(2)两条线段平行应该是这两条线段所在的直线
平行.
解:(1)不正确;
理由:根据定义,它缺少了“在同一平面内”
这一条件.
(2)不正确;
理由:定义中指出的是两条不相交的“直线”,
而不是“线段”.
平行线的定义有三个特征:
一是在同一平面内;
二是不相交;
三是都是直线;三者缺一不可.
新知小结
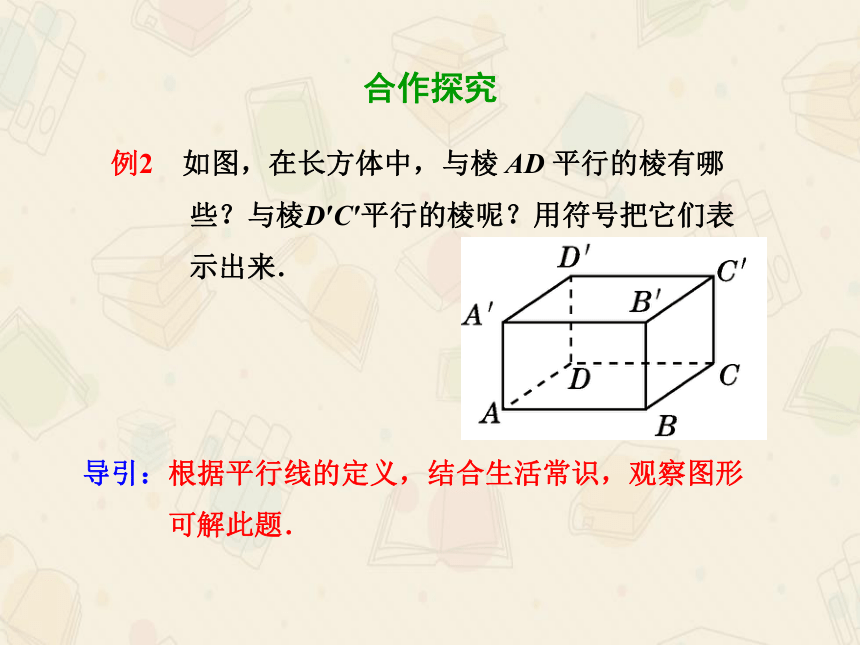
例2 如图,在长方体中,与棱 AD 平行的棱有哪
些?与棱D′C′平行的棱呢?用符号把它们表
示出来.
导引:根据平行线的定义,结合生活常识,观察图形
可解此题.
合作探究
解:与棱AD平行的棱有A′D′,B′C′,BC,
记作AD∥A′D′,AD∥B′C′,AD∥BC.
与棱D′C′平行的棱有DC,AB,A′B′,
记作D′C′∥DC, D′C′∥AB, D′C′∥A′B′.
找平行线要注意两点:
(1)在同一平面内;
(2)不相交(无限延伸).
新知小结
1
下列生活实例中,属于平行线的有( )
①交通路口的斑马线;②黑板的上下边;
③百米直跑道的两边.
A.3个 B.2个
C.1个 D.0个
A
巩固新知
2
下列说法中,正确的有( )
①在同一平面内不相交的两条线段必平行;
②在同一平面内不相交的两条直线必平行;
③在同一平面内不平行的两条线段必相交;
④在同一平面内不平行的两条直线必相交.
A.1个 B.2个 C.3个 D.4个
B
a,b,c是平面内任意三条直线,交点可以有
( )
A.1个或2个或3个
B.0个或1个或2个或3个
C.1个或2个
D.以上都不对
3
B
如图,在长方体的各条棱中,与AB平行的有____________________,与AB相交的有__________________,与AB既不平行又不相交的有________________________.
4
CD、A1B1、C1D1
A1A、B1B、AD、BC
A1D1、B1C1、D1D、C1C
2
知识点
画平行线
你会画平行线吗?
你能在方格纸中画出平行线吗?
b
a
d
c
n
m
t
合作探究
一放
二靠
三移
四画
画出这条直线的平行线
过直线外一点画已知直线的平行线的步骤:
一落:把三角尺的一边落在已知直线上;
二靠:紧靠三角尺的另一边放一直尺;
三移:把这个三角尺沿着直尺移动使其经过已知点;
四画:沿三角尺的一边画直线.此直线即为已知直
线的平行线.
例3 如图,过P点作PQ∥AB交BC于Q,作PM∥
AC交AB于M.
导引:过直线外一点画已知
直线的平行线,要按一
“落”,二“靠”,三“移”,
四“画”的步骤进行.
解:如图.
A
B
C
P
注意“移”时经过点的边是三角尺落在已知直
线上的那一边,而不是任意一边,利用直尺和三角
尺画过直线外一点的已知直线的平行线是几何画图
的基本技能之一.
新知小结
例4 如图,在下面的网格中经过点C画与线段AB
平行的直线 l1,再经过点B画一条与线段AB
垂直的直线 l2.
解:如图.
合作探究
网格中作直线的平行线或垂线时,不需要借
助尺规,直接根据网格的特点作图即可.
新知小结
1
读下列语句,并画出图形:
(1)点P是直线AB外一点,直线CD经过点P,且与
直线AB平行;
(2)直线AB,CD是相交直线,点P是直线AB,CD
外的一点,直线EF经过点 P且与直线AB平行,
与直线CD相交于点E.
巩固新知
解:(1)如图(1)所示.
(2)如图(2)所示.
(1)
(2)
在如图所示的各图形中,过点M画PQ∥AB.
2
解:略.
3
知识点
平行线的基本事实1:确定性
经过点C可以画几条直
线与直线AB平行?
A
B
a
b
(2) 过点D画一条直线与
AB平行.
(3) 通过画图,你发
现了什么?
经过直线外一点,有且只有一条直线与这条直线平行;
C
D
合作探究
例5 下列说法:①过一点有且只有一条直线与已
知直线平行;②一条直线的平行线只有一条;
③过直线外一点,有且只有一条直线与这条
直线平行.其中正确的有( )
A.3个 B.2个 C.1个 D.0个
导引:过直线外一点可以画一条直线与已知直线平行,
而过直线上一点画不出与该直线平行的直线;
一条直线的平行线有无数条,故只有③正确.
C
对于此类辨析题,要正确解答,必须要抓住
相关的内容,特别是关键字词及其重要特征,要
在比较中理解,再在理解的基础上进行记忆.
新知小结
如图,当风车的一片叶子AB旋转到与地面MN平
行时,叶子CD所在的直线与地面MN________,
理由是___________________________________
_____________.
1
相交
经过直线外一点,有且只有一条直线与这条直线平行
巩固新知
已知直线AB和一点P,过点P画直线AB的平行线,可画( )
A.1条 B.0条
C.1条或0条 D.无数条
2
C
在同一平面内,直线m,n相交于点O,且l∥n,则直线l和m的关系是( )
A.平行 B.相交
C.重合 D.以上都有可能
3
B
4
知识点
平行线的基本事实2:传递性
平行公理的推论:如果两条直线都与第三条直线平
行,那么这两条直线也互相平行.简称:同平行于
第三条直线的两直线平行.
表达方式:如果a∥c,b∥c,那么a∥b.
平行公理的推论:可用来判定两直线平行.
合作探究
例6 如图,P是三角形ABC内部的任意一点.
(1)过P点向左画射线PM∥BC交AB于点M,过
P点向右画射线PN∥BC交AC于点N;
(2)在(1)中画出的图形中,∠MPN的度数一定等
于180°,你能说明其中的道理吗?
导引:在(1)中,按照过直线外一点画已知直线的平行线
的方法画图即可.在(2)中,要说明∠MPN=180°,
可转化为说明点M, P, N在同一条直线上.
解:(1)画出的射线PM,PN,如上页图.
(2)因为射线PM∥BC,射线PN∥BC,
所以直线PM∥BC,直线PN∥BC.
所以直线PM与直线PN是同一条直线(过直线外一
点有且只有一条直线与这条直线平行),
即点M, P, N在同一条直线上.所以∠MPN=180°.
本题运用转化思想,把说明∠MPN=180°转
化为说明点M,P,N在同一条直线上,进而把问题
转化为利用有关平行线的基本事实说明直线PM与直
线PN是同一条直线.
新知小结
三条直线l1,l2,l3,若l1∥l3,l2∥l3,则l1与l2的位置关系是( )
A.l1与l2相交
B.l1与l2平行
C.l1与l2相交或l1与l2平行
D.无法确定
1
B
巩固新知
下列说法中,错误的有( )
①若a与c相交,b与c相交,则a与b相交;
②若a∥b,b∥c,则a∥c;
③过直线外一点有且只有一条直线与已知直线平行;④在同一平面内,两条直线的位置关系有平行、相交、垂直三种.
A.3个 B.2个 C.1个 D.0个
2
B
1. 平行线的定义及平面内两直线的位置关系
平行线的定义包含缺一不可的三个条件:
①在同一平面内;②不相交;③都是直线.
2. 平行线的画法
一落、二靠、三移、四画
1
知识小结
归纳新知
3. 平行线的基本事实及其推论
(1)“有且只有”强调直线的存在性和唯一性;
(2)前提条件“经过直线外一点”,若点在直线上,
不可能有平行线.
4. 平行线具有传递性.
下列说法正确的是( )
A.两条不相交的直线叫做平行线
B.过一点有且只有一条直线与已知直线平行
C.在同一平面内不相交的两条线段互相平行
D.在同一平面内不相交的两条直线叫做平行线
2
易错小结
D
对平行线定义的理解要抓住三个关键要素:“同一平面内”“不相交”“直线”,本题易错之处在于理解平行线定义时,容易只关注其中一个或两个条件而导致判断错误.
易错点:对平行线的定义理解不透彻而出错.
在同一平面内
不相交
都是直线
课后练习
相交和平行
【答案】A
C
直线l
靠
移
画
互相垂直
D
平行
平行
b∥c
A
【答案】C
∥
如果两条直线都与第
三条直线平行,那么这两条直线也互相平行
经过直线外一点,有且只有
一条直线与这条直线平行
∥
如果两条直线都与第三条直线平行,那么这两条直线也互
相平行
再见
第五章
5.2.1 平行线
人教版数学七年级下册
看一看,它们有什么共同之处?
扶手
双杠
铁轨
不相交
导入新知
1.理解平行线的意义,了解同一平面内两条直线的位置关系.
2.理解并掌握平行公理及其推论的内容.
3.会根据几何语句画图,会用直尺和三角板画平行线.
4.了解平行线在实际生活中的应用,能举例加以说明.
学习目标
1
知识点
平行线
什么是平行线?
在同一平面内不相交的两条直线叫做平行线.
在同一平面内、
注意
平行线体现三点:
不相交、
两条直线.
在同一平面内
不相交
两条直线
合作探究
平行在生活中的 应用
如果两根铁轨之间的宽度不相等,又会有什么现象发生?
请你想象,手扶电梯左右扶手之间的宽度如果不相等,会出现什么情况?
教室里能找到平行线吗?
我们通常用“//”表示平行.
平行线的表示:
C
D
B
A
m
n
AB ∥ CD
记作:
m ∥ n
记作:
·
·
·
·
例1 判断下列说法是否正确,并说明理由.
(1)不相交的两条直线是平行线;
(2)在同一平面内,两条不相交的线段是平行线.
导引:(1)没有强调两条直线在同一平面内;
(2)两条线段平行应该是这两条线段所在的直线
平行.
解:(1)不正确;
理由:根据定义,它缺少了“在同一平面内”
这一条件.
(2)不正确;
理由:定义中指出的是两条不相交的“直线”,
而不是“线段”.
平行线的定义有三个特征:
一是在同一平面内;
二是不相交;
三是都是直线;三者缺一不可.
新知小结
例2 如图,在长方体中,与棱 AD 平行的棱有哪
些?与棱D′C′平行的棱呢?用符号把它们表
示出来.
导引:根据平行线的定义,结合生活常识,观察图形
可解此题.
合作探究
解:与棱AD平行的棱有A′D′,B′C′,BC,
记作AD∥A′D′,AD∥B′C′,AD∥BC.
与棱D′C′平行的棱有DC,AB,A′B′,
记作D′C′∥DC, D′C′∥AB, D′C′∥A′B′.
找平行线要注意两点:
(1)在同一平面内;
(2)不相交(无限延伸).
新知小结
1
下列生活实例中,属于平行线的有( )
①交通路口的斑马线;②黑板的上下边;
③百米直跑道的两边.
A.3个 B.2个
C.1个 D.0个
A
巩固新知
2
下列说法中,正确的有( )
①在同一平面内不相交的两条线段必平行;
②在同一平面内不相交的两条直线必平行;
③在同一平面内不平行的两条线段必相交;
④在同一平面内不平行的两条直线必相交.
A.1个 B.2个 C.3个 D.4个
B
a,b,c是平面内任意三条直线,交点可以有
( )
A.1个或2个或3个
B.0个或1个或2个或3个
C.1个或2个
D.以上都不对
3
B
如图,在长方体的各条棱中,与AB平行的有____________________,与AB相交的有__________________,与AB既不平行又不相交的有________________________.
4
CD、A1B1、C1D1
A1A、B1B、AD、BC
A1D1、B1C1、D1D、C1C
2
知识点
画平行线
你会画平行线吗?
你能在方格纸中画出平行线吗?
b
a
d
c
n
m
t
合作探究
一放
二靠
三移
四画
画出这条直线的平行线
过直线外一点画已知直线的平行线的步骤:
一落:把三角尺的一边落在已知直线上;
二靠:紧靠三角尺的另一边放一直尺;
三移:把这个三角尺沿着直尺移动使其经过已知点;
四画:沿三角尺的一边画直线.此直线即为已知直
线的平行线.
例3 如图,过P点作PQ∥AB交BC于Q,作PM∥
AC交AB于M.
导引:过直线外一点画已知
直线的平行线,要按一
“落”,二“靠”,三“移”,
四“画”的步骤进行.
解:如图.
A
B
C
P
注意“移”时经过点的边是三角尺落在已知直
线上的那一边,而不是任意一边,利用直尺和三角
尺画过直线外一点的已知直线的平行线是几何画图
的基本技能之一.
新知小结
例4 如图,在下面的网格中经过点C画与线段AB
平行的直线 l1,再经过点B画一条与线段AB
垂直的直线 l2.
解:如图.
合作探究
网格中作直线的平行线或垂线时,不需要借
助尺规,直接根据网格的特点作图即可.
新知小结
1
读下列语句,并画出图形:
(1)点P是直线AB外一点,直线CD经过点P,且与
直线AB平行;
(2)直线AB,CD是相交直线,点P是直线AB,CD
外的一点,直线EF经过点 P且与直线AB平行,
与直线CD相交于点E.
巩固新知
解:(1)如图(1)所示.
(2)如图(2)所示.
(1)
(2)
在如图所示的各图形中,过点M画PQ∥AB.
2
解:略.
3
知识点
平行线的基本事实1:确定性
经过点C可以画几条直
线与直线AB平行?
A
B
a
b
(2) 过点D画一条直线与
AB平行.
(3) 通过画图,你发
现了什么?
经过直线外一点,有且只有一条直线与这条直线平行;
C
D
合作探究
例5 下列说法:①过一点有且只有一条直线与已
知直线平行;②一条直线的平行线只有一条;
③过直线外一点,有且只有一条直线与这条
直线平行.其中正确的有( )
A.3个 B.2个 C.1个 D.0个
导引:过直线外一点可以画一条直线与已知直线平行,
而过直线上一点画不出与该直线平行的直线;
一条直线的平行线有无数条,故只有③正确.
C
对于此类辨析题,要正确解答,必须要抓住
相关的内容,特别是关键字词及其重要特征,要
在比较中理解,再在理解的基础上进行记忆.
新知小结
如图,当风车的一片叶子AB旋转到与地面MN平
行时,叶子CD所在的直线与地面MN________,
理由是___________________________________
_____________.
1
相交
经过直线外一点,有且只有一条直线与这条直线平行
巩固新知
已知直线AB和一点P,过点P画直线AB的平行线,可画( )
A.1条 B.0条
C.1条或0条 D.无数条
2
C
在同一平面内,直线m,n相交于点O,且l∥n,则直线l和m的关系是( )
A.平行 B.相交
C.重合 D.以上都有可能
3
B
4
知识点
平行线的基本事实2:传递性
平行公理的推论:如果两条直线都与第三条直线平
行,那么这两条直线也互相平行.简称:同平行于
第三条直线的两直线平行.
表达方式:如果a∥c,b∥c,那么a∥b.
平行公理的推论:可用来判定两直线平行.
合作探究
例6 如图,P是三角形ABC内部的任意一点.
(1)过P点向左画射线PM∥BC交AB于点M,过
P点向右画射线PN∥BC交AC于点N;
(2)在(1)中画出的图形中,∠MPN的度数一定等
于180°,你能说明其中的道理吗?
导引:在(1)中,按照过直线外一点画已知直线的平行线
的方法画图即可.在(2)中,要说明∠MPN=180°,
可转化为说明点M, P, N在同一条直线上.
解:(1)画出的射线PM,PN,如上页图.
(2)因为射线PM∥BC,射线PN∥BC,
所以直线PM∥BC,直线PN∥BC.
所以直线PM与直线PN是同一条直线(过直线外一
点有且只有一条直线与这条直线平行),
即点M, P, N在同一条直线上.所以∠MPN=180°.
本题运用转化思想,把说明∠MPN=180°转
化为说明点M,P,N在同一条直线上,进而把问题
转化为利用有关平行线的基本事实说明直线PM与直
线PN是同一条直线.
新知小结
三条直线l1,l2,l3,若l1∥l3,l2∥l3,则l1与l2的位置关系是( )
A.l1与l2相交
B.l1与l2平行
C.l1与l2相交或l1与l2平行
D.无法确定
1
B
巩固新知
下列说法中,错误的有( )
①若a与c相交,b与c相交,则a与b相交;
②若a∥b,b∥c,则a∥c;
③过直线外一点有且只有一条直线与已知直线平行;④在同一平面内,两条直线的位置关系有平行、相交、垂直三种.
A.3个 B.2个 C.1个 D.0个
2
B
1. 平行线的定义及平面内两直线的位置关系
平行线的定义包含缺一不可的三个条件:
①在同一平面内;②不相交;③都是直线.
2. 平行线的画法
一落、二靠、三移、四画
1
知识小结
归纳新知
3. 平行线的基本事实及其推论
(1)“有且只有”强调直线的存在性和唯一性;
(2)前提条件“经过直线外一点”,若点在直线上,
不可能有平行线.
4. 平行线具有传递性.
下列说法正确的是( )
A.两条不相交的直线叫做平行线
B.过一点有且只有一条直线与已知直线平行
C.在同一平面内不相交的两条线段互相平行
D.在同一平面内不相交的两条直线叫做平行线
2
易错小结
D
对平行线定义的理解要抓住三个关键要素:“同一平面内”“不相交”“直线”,本题易错之处在于理解平行线定义时,容易只关注其中一个或两个条件而导致判断错误.
易错点:对平行线的定义理解不透彻而出错.
在同一平面内
不相交
都是直线
课后练习
相交和平行
【答案】A
C
直线l
靠
移
画
互相垂直
D
平行
平行
b∥c
A
【答案】C
∥
如果两条直线都与第
三条直线平行,那么这两条直线也互相平行
经过直线外一点,有且只有
一条直线与这条直线平行
∥
如果两条直线都与第三条直线平行,那么这两条直线也互
相平行
再见
