江西省抚州市七校2020-2021学年高二下学期期末联考物理试卷(Word版含答案)
文档属性
| 名称 | 江西省抚州市七校2020-2021学年高二下学期期末联考物理试卷(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 417.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-12-30 17:53:13 | ||
图片预览




文档简介
2020-2021学年江西省抚州市七校联考高二(下)期末物理试卷
一、选择题(本大题共10小题,每小题4分,共40分)
1.(4分)第一位提出“光本身也是一种电磁波”的科学家是( )
A.赫兹 B.法拉第 C.麦克斯韦 D.爱因斯坦
2.(4分)在光电效应实验中,用单色光照射光电管阴极,发生了光电效应.要使光电管中的电流增大,下列做法正确的是( )
A.保持入射光的频率不变,增加照射时间
B.保持入射光的频率不变,增大光的强度
C.保持入射光的强度不变,增加照射时间
D.保持入射光的强度不变,增大光的频率
3.(4分)一束光由空气射向一块平行平面玻璃砖,折射后分为两束单色光a、b.下列判断正确的是( )
A.在玻璃砖中a光的速度大于b光的速度,射出玻璃砖后单色光a、b平行
B.在玻璃砖中a光的速度大于b光的速度,射出玻璃砖后单色光a、b不平行
C.在玻璃砖中a光的速度小于b光的速度,射出玻璃砖后单色光a、b平行
D.在玻璃砖中a光的速度小于b光的速度,射出玻璃砖后单色光a、b不平行
4.(4分)如图所示是双缝干涉的实验装置,使用波长为600nm的橙色光照射单缝S,在光屏中央P处观察到亮条纹,在位于P的上方的P1处出现第一条亮纹中心,现换用波长为400nm的紫色光照射单缝S,则( )
A.P和P1处都为亮条纹
B.P和P1处都为暗条纹
C.P处是亮条纹,P1处是暗条纹
D.P处是暗条纹,P1处是亮条纹
5.(4分)实验观察到,静止在匀强磁场中A点的原子核发生β衰变,衰变产生的新核与β粒子恰在纸面内做匀速圆周运动,粒子的轨迹如图所示,其中粒子在轨迹1是按顺时针方向运动.则( )
A.轨迹1是新核的,粒子在轨迹2是按顺时针方向活动
B.轨迹2是新核的,粒子在轨迹2是按顺时针方向运动
C.轨迹1是新核的,粒子在轨迹2是按逆时针方向运动
D.轨迹2是新核的,粒子在轨迹2是按逆时针方向运动
6.(4分)如图所示,斜面体固定在水平地面上,斜面表面是光滑的且足够长.斜面顶端与自然长度为L的轻质弹簧相连,弹簧的另一端连接着物块m,当物块静止时,弹簧的伸长量为△l.压缩弹簧使弹簧长度为L时将物块由静止释放,则物块运动过程中,弹簧的最大伸长量为(运动过程中弹簧未超过弹性限度)
A.+2△l B.+△l C.L+2△l D.L+△l
7.(4分)运动的原子核X放出α粒子后变成静止的原子核Y.已知原子核X、α粒子的质量分别是M、m,α粒子的动能为E,真空中的光速为c,α粒子的速度远小于光速.则在上述核反应中的质量亏损是( )
A. B.E C.E D.E
8.(4分)氢原子基态的能量为E1=﹣13.6eV.大量氢原子处于某一激发态.由这些氢原子可能发出的所有光子中,频率最大的光子能量为﹣0.96E1,则( )
A.频率最小的光子能量为0.31eV
B.频率最小的光子能量为0.54eV
C.发出的光子具有4种不同的频率
D.发出的光子具有10种不同的频率
9.(4分)一列简谐横波在均匀介质中沿直线传播,P、Q是传播方向上相距10m的两个质点。波先传到P,当波传到Q开始计时,P、Q两质点的振动图象如图所示,则( )
A.质点Q开始振动的方向沿y轴正方向
B.该波从P点传到Q的最短时间为2s
C.该波波长的最大值为15m
D.该波的传播速度可能为m/s
10.(4分)如图所示,光滑水平面上A、B两小球沿同一方向运动,A球的动量4kg m/s,B球的质量1kg,速度为6m/s,已知两球相碰后,A球的动量减为原来的一半,方向与原方向一致.则( )
A.A球的质量可能为0.4kg
B.A球的质量可能为0.5kg
C.A球碰撞后的速度不可能为4m/s
D.A球碰撞后的速度不可能为10m/s
二、非选择题(本大题共6小题,共60分)
11.(8分)利用单摆测量当地的重力加速度,如图甲所示,将长约为1m的细线上端固定在铁架台上,下端系一小钢球,就做成了单摆.
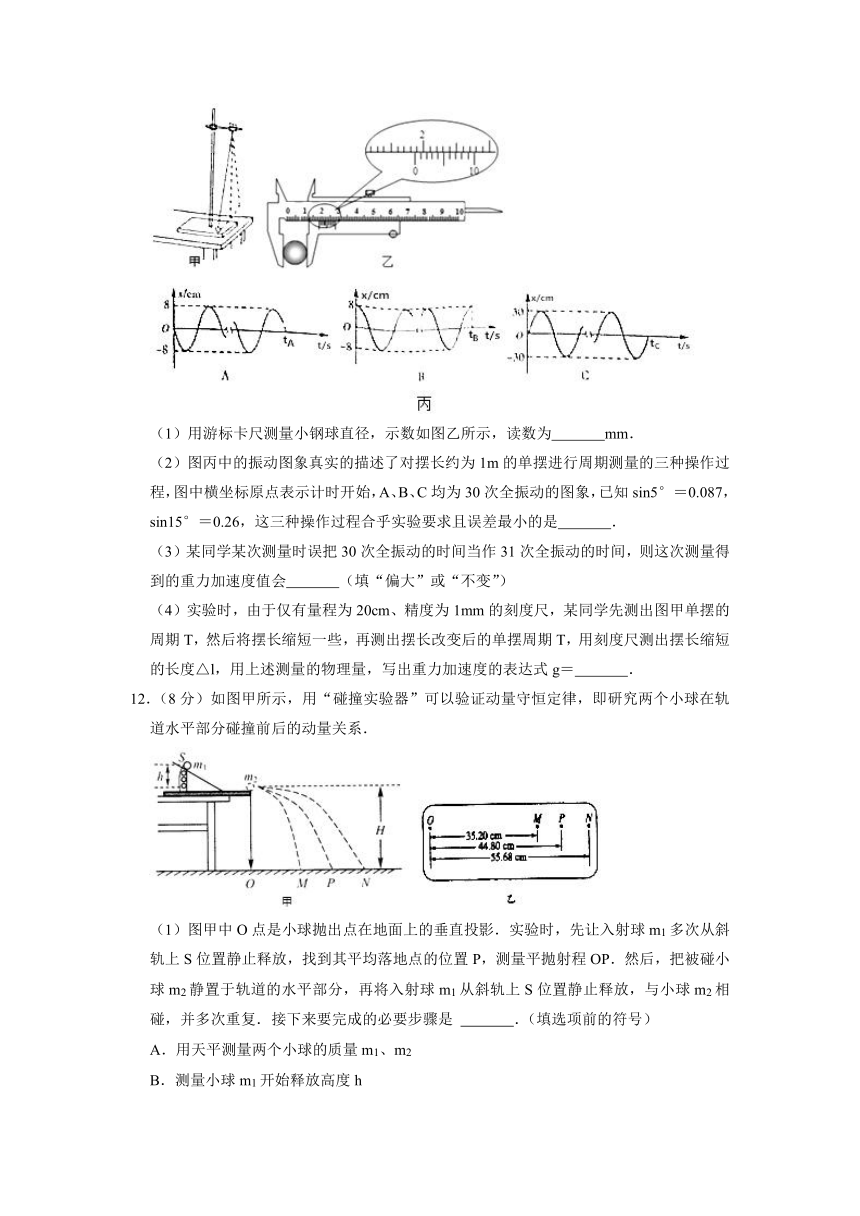
(1)用游标卡尺测量小钢球直径,示数如图乙所示,读数为 mm.
(2)图丙中的振动图象真实的描述了对摆长约为1m的单摆进行周期测量的三种操作过程,图中横坐标原点表示计时开始,A、B、C均为30次全振动的图象,已知sin5°=0.087,sin15°=0.26,这三种操作过程合乎实验要求且误差最小的是 .
(3)某同学某次测量时误把30次全振动的时间当作31次全振动的时间,则这次测量得到的重力加速度值会 (填“偏大”或“不变”)
(4)实验时,由于仅有量程为20cm、精度为1mm的刻度尺,某同学先测出图甲单摆的周期T,然后将摆长缩短一些,再测出摆长改变后的单摆周期T,用刻度尺测出摆长缩短的长度△l,用上述测量的物理量,写出重力加速度的表达式g= .
12.(8分)如图甲所示,用“碰撞实验器”可以验证动量守恒定律,即研究两个小球在轨道水平部分碰撞前后的动量关系.
(1)图甲中O点是小球抛出点在地面上的垂直投影.实验时,先让入射球m1多次从斜轨上S位置静止释放,找到其平均落地点的位置P,测量平抛射程OP.然后,把被碰小球m2静置于轨道的水平部分,再将入射球m1从斜轨上S位置静止释放,与小球m2相碰,并多次重复.接下来要完成的必要步骤是 .(填选项前的符号)
A.用天平测量两个小球的质量m1、m2
B.测量小球m1开始释放高度h
C.测量抛出点距离地面的高度H
D.分别找到m1、m2相碰后平均落地点的位置M、N
E.测量平抛射程OM、ON
(2)经测定,m1=45.0g,m2=7.5g,小球落地点的平均位置距O点的距离如图乙所示.实验结果说明,碰撞前、后总动量的比值为 (用(1)中测量的量表示),代入数值求得这个比值为 .
(3)在上述实验中仅更换两个小球的材质,其他条件不变,可以使被碰小球做平抛运动的射程增大,请用(2)中已知的数据,计算出被碰小球m2平抛运动射程ON的最大值为 cm.
13.(8分)如图所示,一列简谐横波沿x轴传播,实线是这列波在t1=0时刻的波形,虚线是这列波在t2=0.5s时刻的波形,问:
(1)若这列波的波速大小为74m/s,求波传播的方向?
(2)若这列波的周期为T,且3T<t2﹣t1<4T,求这列波的波速是多大?
14.(10分)如图所示,横截面为四分之一圆的柱形玻璃砖放在水平面MN上,O点是圆心.一列与OA面等高的平行光束沿水平方向垂直射向玻璃砖的OA面,平行光束通过玻璃砖后在水平面MN上留下照亮的区域.已知玻璃砖的折射率为n(n<2),不考虑光在OA、OB面的反射.求:
(1)若在玻璃砖左侧竖直放置一遮光板,使水平面BN不被照亮,遮光板的最小高度是多少?
(2)撤去遮光板,从OA的中点射入的光,在MN上的P处留下一个光点,P点到O点的距离是多少?
15.(12分)如图所示,木板的质量为2m,长为L,静止在光滑的水平地面上,木板上下面均与地面平行.点A、B是木板的两个端点,点C是中点,AC段是光滑的,CB段是粗糙的,木板的A端放有一个质量为m的物块(可视为质点),现给木板一个瞬间冲量,使木板获得一个水平向右、大小为v0的速度,最终物块恰好滑到木板的B端与木板一起运动.求:
(1)物块滑到木板B点时木板的速度v;
(3)物块在AB段上滑行的时间t.
16.(14分)如图所示,A、B、C三个小物块放置在光滑水平面上,A紧靠在墙壁,A、B之间用轻弹簧连接,它们的质量分别为mA=m,mB=2m,mC=m.现使物块C获得水平向左的初速度v0,物块C与物块B发生碰撞并粘在一起不再分离.试求:
(1)物块A离开墙前,弹簧的最大弹性势能Em;
(2)物块A离开墙后,物块C的最小速度vmin.
参考答案与试题解析
一、选择题(本大题共10小题,每小题4分,共40分)
1.(4分)第一位提出“光本身也是一种电磁波”的科学家是( )
A.赫兹 B.法拉第 C.麦克斯韦 D.爱因斯坦
【解答】解:建立完整电磁场理论并首先预言电磁波存在的科学家是麦克斯韦,而赫兹证实了电磁波的存在,对于法拉第首次提出场的概念,并发现电磁感应现象,爱因斯坦的相对论。故C正确,ABD错误。
故选:C。
2.(4分)在光电效应实验中,用单色光照射光电管阴极,发生了光电效应.要使光电管中的电流增大,下列做法正确的是( )
A.保持入射光的频率不变,增加照射时间
B.保持入射光的频率不变,增大光的强度
C.保持入射光的强度不变,增加照射时间
D.保持入射光的强度不变,增大光的频率
【解答】解:A、保持入射光的频率不变,增加照射时间只能增加产生光电效应的时间,与饱和光电流无关。故A错误;
B、保持入射光的频率不变,光照强度增大,单位时间内照射到金属表面的光子数目增大,因此单位时间内产生的光电子数目增大,即饱和电流增大,故B正确;
C、结合B的方向可知,保持入射光的强度不变,不能判断出是否增大饱和光电流。故C错误;
D、保持入射光的强度不变,增大光的频率,则单个的光子的能量增大,所以单位时间内入射的光子的数目减少,所以单位时间内产生的光电子减少,所以饱和光电流减小。故D错误。
故选:B。
3.(4分)一束光由空气射向一块平行平面玻璃砖,折射后分为两束单色光a、b.下列判断正确的是( )
A.在玻璃砖中a光的速度大于b光的速度,射出玻璃砖后单色光a、b平行
B.在玻璃砖中a光的速度大于b光的速度,射出玻璃砖后单色光a、b不平行
C.在玻璃砖中a光的速度小于b光的速度,射出玻璃砖后单色光a、b平行
D.在玻璃砖中a光的速度小于b光的速度,射出玻璃砖后单色光a、b不平行
【解答】解:由光路图可知,b光的偏折程度较大,则b光的折射率大,根据v=知,b光在玻璃砖中传播的速度较小,光线在玻璃砖的上表面的折射角和下表面的入射角相等,根据光的可逆原理知,光线在下表面的折射角与上表面的入射角相等,可知射出玻璃砖后单色光a、b平行。故A正确,B、C、D错误。
故选:A。
4.(4分)如图所示是双缝干涉的实验装置,使用波长为600nm的橙色光照射单缝S,在光屏中央P处观察到亮条纹,在位于P的上方的P1处出现第一条亮纹中心,现换用波长为400nm的紫色光照射单缝S,则( )
A.P和P1处都为亮条纹
B.P和P1处都为暗条纹
C.P处是亮条纹,P1处是暗条纹
D.P处是暗条纹,P1处是亮条纹
【解答】解:缝S1、S2到光屏中央P点的距离相等,无论什么色光,其相干光的路程差均为0,故P处都是亮条纹。对于波长为600nm的橙色光,S1、S2到P1点的路程差恰好为橙色光的1个波长,则换用波长为400nm的紫色光时,S1、S2到P1点的路程差恰好为橙色光的1.5个波长,因此紫色光照射时在P1处是暗条纹。故C正确,A、B、D错误。
故选:C。
5.(4分)实验观察到,静止在匀强磁场中A点的原子核发生β衰变,衰变产生的新核与β粒子恰在纸面内做匀速圆周运动,粒子的轨迹如图所示,其中粒子在轨迹1是按顺时针方向运动.则( )
A.轨迹1是新核的,粒子在轨迹2是按顺时针方向活动
B.轨迹2是新核的,粒子在轨迹2是按顺时针方向运动
C.轨迹1是新核的,粒子在轨迹2是按逆时针方向运动
D.轨迹2是新核的,粒子在轨迹2是按逆时针方向运动
【解答】解:原子核发生β衰变时,根据动量守恒可知两粒子的速度方向相反,动量的方向相反,大小相等;
由半径公式r==(P是动量),分析得知,r与电荷量成反比,β粒子与新核的电量大小分别为e和ne(n为新核的电荷数),则β粒子与新核的半径之比为:ne:e=n:1。
所以半径比较大的轨迹1是衰变后β粒子的轨迹,轨迹2是新核的。
新核沿逆时针方向运动,在A点受到的洛伦兹力向左,由左手定则可知,磁场的方向向里。
由以上的分析可知,选项D正确,ABC错误。
故选:D。
6.(4分)如图所示,斜面体固定在水平地面上,斜面表面是光滑的且足够长.斜面顶端与自然长度为L的轻质弹簧相连,弹簧的另一端连接着物块m,当物块静止时,弹簧的伸长量为△l.压缩弹簧使弹簧长度为L时将物块由静止释放,则物块运动过程中,弹簧的最大伸长量为(运动过程中弹簧未超过弹性限度)
A.+2△l B.+△l C.L+2△l D.L+△l
【解答】解:由题,当物块静止时,弹簧的伸长量为△l;根据简谐运动的对称性,压缩弹簧使其长度为L时将物块由静止开始释放,故其振幅为:
A=L+△l
故其最大伸长量为:A+△l=L+2△l
故A正确,BCD错误
故选:A。
7.(4分)运动的原子核X放出α粒子后变成静止的原子核Y.已知原子核X、α粒子的质量分别是M、m,α粒子的动能为E,真空中的光速为c,α粒子的速度远小于光速.则在上述核反应中的质量亏损是( )
A. B.E C.E D.E
【解答】解:核反应中动量守恒,有:mvα=Mvx,
α粒子的动能为E=,
根据能量守恒得,,
由爱因斯坦质能方程得,△E=△mc2,
联立解得,故B正确,A、C、D错误。
故选:B。
8.(4分)氢原子基态的能量为E1=﹣13.6eV.大量氢原子处于某一激发态.由这些氢原子可能发出的所有光子中,频率最大的光子能量为﹣0.96E1,则( )
A.频率最小的光子能量为0.31eV
B.频率最小的光子能量为0.54eV
C.发出的光子具有4种不同的频率
D.发出的光子具有10种不同的频率
【解答】解:AB、氢原子基态的能量为E1=﹣13.6eV.大量氢原子处于某一激发态。
由这些氢原子可能发出的所有光子中,频率最大的光子能量为﹣0.96E1,即跃迁到最高能级能量E=0.04E1=﹣0.544eV,即处在n=5能级;
频率最小的光子的能量为△E′=﹣0.544eV﹣(﹣0.85eV)=0.31eV,故A正确,B错误;
CD、根据数学组合公式,=10,所以这些光子可具有10种不同的频率,故C错误,D正确。
故选:AD。
9.(4分)一列简谐横波在均匀介质中沿直线传播,P、Q是传播方向上相距10m的两个质点。波先传到P,当波传到Q开始计时,P、Q两质点的振动图象如图所示,则( )
A.质点Q开始振动的方向沿y轴正方向
B.该波从P点传到Q的最短时间为2s
C.该波波长的最大值为15m
D.该波的传播速度可能为m/s
【解答】解:A、根据y﹣t图象的斜率表示速度,知质点Q的起振方向沿y轴正方向,故A正确。
B、由题可知,简谐横波的传播方向从P到Q,由图可知,周期T=6s,质点Q的振动图象向左平移4s后与P点的振动图象重合,意味着Q点比P点振动最少滞后了4s,即P传到Q的时间△t至少为4s,由周期性可知,从P传到Q的时间△t=(4+nT)s,n=0、1、2、3…,即△t=4s,10s,16s…,不可能为2s,故B错误。
CD、由v==m/s,可知,当△t=4s,10s,16s…时,速度v可能为2.5m/s,1m/s,0.625m/s…,不可能为m/s。
由λ=vT,代入最大波速为2.5m/s时,求得波长的最大值为15m,故C正确,D错误。
故选:AC。
10.(4分)如图所示,光滑水平面上A、B两小球沿同一方向运动,A球的动量4kg m/s,B球的质量1kg,速度为6m/s,已知两球相碰后,A球的动量减为原来的一半,方向与原方向一致.则( )
A.A球的质量可能为0.4kg
B.A球的质量可能为0.5kg
C.A球碰撞后的速度不可能为4m/s
D.A球碰撞后的速度不可能为10m/s
【解答】解:AB、由题知,碰撞后A的动量为 p'A=2kg m/s,根据动量守恒定律有:pA+mBvB=p'A+mBv'B,解得 v'B=8.0m/s。
设A球质量为mA,A球能追上B球并与之碰撞,应满足 vA=>vB;碰撞后A球不可能运动到B球前方,故v′A=≤v′B;
碰撞过程系统的总动能不可能增加,故+mBvB2≤+mBvB′2
解得:kg≤mA≤kg(或0.25kg≤mA≤0.43kg),所以A球的质量可能为0.4kg,不可能为0.5kg,故A正确,B错误。
CD、碰撞后,B球的速度为v'B=8.0m/s,则A球碰撞后的速度不可能大于8.0m/s,所以A球碰撞后的速度不可能为10m/s。
若A球的质量为0.5kg,则碰撞前A球的速度为8m/s,碰撞后的速度为4m/s,碰撞前后A球动能的减少△EkA=﹣=﹣=12J
B球动能的增加量△EkB=mBvB′2﹣mBvB2=14J>△EkA,不可能,故CD正确。
故选:ACD。
二、非选择题(本大题共6小题,共60分)
11.(8分)利用单摆测量当地的重力加速度,如图甲所示,将长约为1m的细线上端固定在铁架台上,下端系一小钢球,就做成了单摆.
(1)用游标卡尺测量小钢球直径,示数如图乙所示,读数为 18.6 mm.
(2)图丙中的振动图象真实的描述了对摆长约为1m的单摆进行周期测量的三种操作过程,图中横坐标原点表示计时开始,A、B、C均为30次全振动的图象,已知sin5°=0.087,sin15°=0.26,这三种操作过程合乎实验要求且误差最小的是 A .
(3)某同学某次测量时误把30次全振动的时间当作31次全振动的时间,则这次测量得到的重力加速度值会 偏大 (填“偏大”或“不变”)
(4)实验时,由于仅有量程为20cm、精度为1mm的刻度尺,某同学先测出图甲单摆的周期T,然后将摆长缩短一些,再测出摆长改变后的单摆周期T,用刻度尺测出摆长缩短的长度△l,用上述测量的物理量,写出重力加速度的表达式g= .
【解答】解:(1)由图示游标卡尺可知,其示数为18mm+6×0.1mm=18.6mm.
(2)单摆的振动在摆角小于5°才能看作简谐振动,在测量周期时计时起点应该选择在平衡位置(速度大误差小).根据摆角估算振幅 A1=lsin5°=1×0.087m=0.087m=8.7cm≈8cm,AB振幅合理; A2=lsin15°=1×0.26m=0.26m=26cm,C振幅不合理,A中振动图象的计时起点在平衡位置是合理的,B中振动图象的计时起点在正的最大位置是不合理的,
故选:A;
(3)由单摆周期公式:T=2π可知重力加速度为:g=;误把30次全振动的时间当作31次全振动的时间,所测周期T偏小,则所测得的重力加速度值会偏大.
(4)由单摆周期公式得:T1=2π,T2=2π
解得:g=;
故答案为:(1)18.6;(2)A;(3)偏大;(4).
12.(8分)如图甲所示,用“碰撞实验器”可以验证动量守恒定律,即研究两个小球在轨道水平部分碰撞前后的动量关系.
(1)图甲中O点是小球抛出点在地面上的垂直投影.实验时,先让入射球m1多次从斜轨上S位置静止释放,找到其平均落地点的位置P,测量平抛射程OP.然后,把被碰小球m2静置于轨道的水平部分,再将入射球m1从斜轨上S位置静止释放,与小球m2相碰,并多次重复.接下来要完成的必要步骤是 ADE .(填选项前的符号)
A.用天平测量两个小球的质量m1、m2
B.测量小球m1开始释放高度h
C.测量抛出点距离地面的高度H
D.分别找到m1、m2相碰后平均落地点的位置M、N
E.测量平抛射程OM、ON
(2)经测定,m1=45.0g,m2=7.5g,小球落地点的平均位置距O点的距离如图乙所示.实验结果说明,碰撞前、后总动量的比值为 (用(1)中测量的量表示),代入数值求得这个比值为 1 .
(3)在上述实验中仅更换两个小球的材质,其他条件不变,可以使被碰小球做平抛运动的射程增大,请用(2)中已知的数据,计算出被碰小球m2平抛运动射程ON的最大值为 76.8 cm.
【解答】解:(1)A、小球的动量P=mv,实验需要用天平测量两个小球的质量m1、m2,故A正确;
B、只要每次从斜槽的同一位置由静止释放小球即可,不需要测量小球m1开始释放高度h,故B错误;
C、两球离开轨道后都做平抛运动,它们抛出点的高度相同,运动时间t相等,在表达式中t可以约去,实验不需要测量抛出点距离地面的高度H,故C错误;
D、小球离开轨道后做平抛运动,它们抛出点的高度相等,在空中的运动时间相等,可以用它们的水平位移代替初速度,实验需要分别找到m1、m2相碰后平均落地点的位置M、N,需要测量平抛射程OM、ON,故DE正确;
故选:ADE.
(2)由图示可知,P点是碰撞前入射球的落点,M、N分别是碰撞后入射球与被碰球的落点,
要验证动量守恒定律定律,即验证:m1v1=m1v2+m2v3,小球离开轨道后做平抛运动,
它们抛出点的高度相等,在空中的运动时间t相等,上式两边同时乘以t得:
m1v1t=m1v2t+m2v3t,得:m1OP=m1OM+m2ON,碰撞前后总动量的比值:
===1;
(3)两球发生弹性碰撞时,被碰小球获得速度最大,其水平射程最大,
以向右为正方向,由动量守恒定律得:m1v0=m1v1+m2v2,
由机械能守恒定律得:m1v02=m1v12+m2v22,
得动能守恒的表达式是:m1 OM2+m2 ON2=m1 OP2,
解得:v2=v0,
因此最大射程为:sm= OP=×44.80cm=76.8cm;
故答案为:(1)ADE;(2);1;(3)76.8.
13.(8分)如图所示,一列简谐横波沿x轴传播,实线是这列波在t1=0时刻的波形,虚线是这列波在t2=0.5s时刻的波形,问:
(1)若这列波的波速大小为74m/s,求波传播的方向?
(2)若这列波的周期为T,且3T<t2﹣t1<4T,求这列波的波速是多大?
【解答】解:(1)由图象可知:该波的波长 λ=8m。
若波速大小为74m/s,在△t=t2﹣t1=0.5s内波传播的距离为△x=v △t=74×0.5m=37m
因为=4
所以波沿x轴负方向传播;
(2)波在一个周期内传播的距离是一个波长,由3T<t2﹣t1<4T知,波传播距离为3λ<△x<4λ。
当波向x轴正方向传播时,波传播距离为:x=(3λ+3)m=(3×8+3)m=27m
波速为:v==m/s=54m/s;
当波向x轴负方向传播时,波传播距离为 x=(3λ+5)m=(3×8+5)m=29m
波速为:v═=m/s=58m/s。
答:(1)若这列波的波速大小为74m/s,波沿x轴负方向传播;
(2)当波向x轴正方向传播时,波速为54m/s;
当波向x轴负方向传播时,波速为58m/s。
14.(10分)如图所示,横截面为四分之一圆的柱形玻璃砖放在水平面MN上,O点是圆心.一列与OA面等高的平行光束沿水平方向垂直射向玻璃砖的OA面,平行光束通过玻璃砖后在水平面MN上留下照亮的区域.已知玻璃砖的折射率为n(n<2),不考虑光在OA、OB面的反射.求:
(1)若在玻璃砖左侧竖直放置一遮光板,使水平面BN不被照亮,遮光板的最小高度是多少?
(2)撤去遮光板,从OA的中点射入的光,在MN上的P处留下一个光点,P点到O点的距离是多少?
【解答】解:(1)如图1,当光线在AB面入射角大于临界角C时,将没有光线出射后射向BN平面,设遮光板高度为h,则
由折射定律有:sinC=,
由几何知识得h=RsinC
求得h=.
(2)如图2,当光在AB面中点入射时,入射角为30°,设P点到O点的距离为S,
由折射定律,
解得sinθ=,cosθ=,
在直角△OEP中,θ=30+γ
根据正弦定律有:,
因此S=R==,
代入θ的正弦值和余弦值,求得P点到O点的距离S=.
答:(1)遮光板的最小高度是;
(2)P点到O点的距离是.
15.(12分)如图所示,木板的质量为2m,长为L,静止在光滑的水平地面上,木板上下面均与地面平行.点A、B是木板的两个端点,点C是中点,AC段是光滑的,CB段是粗糙的,木板的A端放有一个质量为m的物块(可视为质点),现给木板一个瞬间冲量,使木板获得一个水平向右、大小为v0的速度,最终物块恰好滑到木板的B端与木板一起运动.求:
(1)物块滑到木板B点时木板的速度v;
(3)物块在AB段上滑行的时间t.
【解答】解:(1)在运动过程中,木板和物块组成的系统动量守恒,取向右为正方向,由动量守恒定律得:
2mv0=(2m+m)v
解得:v=
(2)设物块在AC段滑行时间为t1,在CB段滑行时间为t2,则有:
=v0t1.
=﹣.
解得:t=t1+t2=
答:(1)物块滑到木板B点时木板的速度v是;
(2)物块在AB段上滑行的时间t是.
16.(14分)如图所示,A、B、C三个小物块放置在光滑水平面上,A紧靠在墙壁,A、B之间用轻弹簧连接,它们的质量分别为mA=m,mB=2m,mC=m.现使物块C获得水平向左的初速度v0,物块C与物块B发生碰撞并粘在一起不再分离.试求:
(1)物块A离开墙前,弹簧的最大弹性势能Em;
(2)物块A离开墙后,物块C的最小速度vmin.
【解答】解:(1)设物块C与B发生碰撞粘在一起时的速度为v.C、B碰撞过程,选取向左为正方向,根据动量守恒定律得:
mcv0=(mc+mB)v
得:v=v0.
当C与B一起压缩弹簧至速度为零时弹簧的弹性势能最大.以B、C和弹簧组成的系统为研究对象,根据机械能守恒定律有:
Em=(mc+mB)2.
联立以上两式解得:Em=.
(2)在A离开墙壁时,弹簧第一次恢复原长,B、C以速度v向右运动;
在A离开墙壁后,由于弹簧的作用,A的速度逐渐增大,B、C的速度逐渐减小,当弹簧再次恢复原长时,B与C的速度最小.设B与C的速度最小时A的速度为vA.
选取向右为正方向,由A、B、C三物体组成系统动量守恒得:
(mB+mC)v=mAvA+(mB+mC)vmin
又由能量守恒定律有:(mB+mC)v2=mAvA2+(mB+mC)vmin2
联立解得:vmin=
答:(1)A离开墙前,弹簧的最大弹性势能Em为.
(2)物块A离开墙后,物块C的最小速度vmin为.
一、选择题(本大题共10小题,每小题4分,共40分)
1.(4分)第一位提出“光本身也是一种电磁波”的科学家是( )
A.赫兹 B.法拉第 C.麦克斯韦 D.爱因斯坦
2.(4分)在光电效应实验中,用单色光照射光电管阴极,发生了光电效应.要使光电管中的电流增大,下列做法正确的是( )
A.保持入射光的频率不变,增加照射时间
B.保持入射光的频率不变,增大光的强度
C.保持入射光的强度不变,增加照射时间
D.保持入射光的强度不变,增大光的频率
3.(4分)一束光由空气射向一块平行平面玻璃砖,折射后分为两束单色光a、b.下列判断正确的是( )
A.在玻璃砖中a光的速度大于b光的速度,射出玻璃砖后单色光a、b平行
B.在玻璃砖中a光的速度大于b光的速度,射出玻璃砖后单色光a、b不平行
C.在玻璃砖中a光的速度小于b光的速度,射出玻璃砖后单色光a、b平行
D.在玻璃砖中a光的速度小于b光的速度,射出玻璃砖后单色光a、b不平行
4.(4分)如图所示是双缝干涉的实验装置,使用波长为600nm的橙色光照射单缝S,在光屏中央P处观察到亮条纹,在位于P的上方的P1处出现第一条亮纹中心,现换用波长为400nm的紫色光照射单缝S,则( )
A.P和P1处都为亮条纹
B.P和P1处都为暗条纹
C.P处是亮条纹,P1处是暗条纹
D.P处是暗条纹,P1处是亮条纹
5.(4分)实验观察到,静止在匀强磁场中A点的原子核发生β衰变,衰变产生的新核与β粒子恰在纸面内做匀速圆周运动,粒子的轨迹如图所示,其中粒子在轨迹1是按顺时针方向运动.则( )
A.轨迹1是新核的,粒子在轨迹2是按顺时针方向活动
B.轨迹2是新核的,粒子在轨迹2是按顺时针方向运动
C.轨迹1是新核的,粒子在轨迹2是按逆时针方向运动
D.轨迹2是新核的,粒子在轨迹2是按逆时针方向运动
6.(4分)如图所示,斜面体固定在水平地面上,斜面表面是光滑的且足够长.斜面顶端与自然长度为L的轻质弹簧相连,弹簧的另一端连接着物块m,当物块静止时,弹簧的伸长量为△l.压缩弹簧使弹簧长度为L时将物块由静止释放,则物块运动过程中,弹簧的最大伸长量为(运动过程中弹簧未超过弹性限度)
A.+2△l B.+△l C.L+2△l D.L+△l
7.(4分)运动的原子核X放出α粒子后变成静止的原子核Y.已知原子核X、α粒子的质量分别是M、m,α粒子的动能为E,真空中的光速为c,α粒子的速度远小于光速.则在上述核反应中的质量亏损是( )
A. B.E C.E D.E
8.(4分)氢原子基态的能量为E1=﹣13.6eV.大量氢原子处于某一激发态.由这些氢原子可能发出的所有光子中,频率最大的光子能量为﹣0.96E1,则( )
A.频率最小的光子能量为0.31eV
B.频率最小的光子能量为0.54eV
C.发出的光子具有4种不同的频率
D.发出的光子具有10种不同的频率
9.(4分)一列简谐横波在均匀介质中沿直线传播,P、Q是传播方向上相距10m的两个质点。波先传到P,当波传到Q开始计时,P、Q两质点的振动图象如图所示,则( )
A.质点Q开始振动的方向沿y轴正方向
B.该波从P点传到Q的最短时间为2s
C.该波波长的最大值为15m
D.该波的传播速度可能为m/s
10.(4分)如图所示,光滑水平面上A、B两小球沿同一方向运动,A球的动量4kg m/s,B球的质量1kg,速度为6m/s,已知两球相碰后,A球的动量减为原来的一半,方向与原方向一致.则( )
A.A球的质量可能为0.4kg
B.A球的质量可能为0.5kg
C.A球碰撞后的速度不可能为4m/s
D.A球碰撞后的速度不可能为10m/s
二、非选择题(本大题共6小题,共60分)
11.(8分)利用单摆测量当地的重力加速度,如图甲所示,将长约为1m的细线上端固定在铁架台上,下端系一小钢球,就做成了单摆.
(1)用游标卡尺测量小钢球直径,示数如图乙所示,读数为 mm.
(2)图丙中的振动图象真实的描述了对摆长约为1m的单摆进行周期测量的三种操作过程,图中横坐标原点表示计时开始,A、B、C均为30次全振动的图象,已知sin5°=0.087,sin15°=0.26,这三种操作过程合乎实验要求且误差最小的是 .
(3)某同学某次测量时误把30次全振动的时间当作31次全振动的时间,则这次测量得到的重力加速度值会 (填“偏大”或“不变”)
(4)实验时,由于仅有量程为20cm、精度为1mm的刻度尺,某同学先测出图甲单摆的周期T,然后将摆长缩短一些,再测出摆长改变后的单摆周期T,用刻度尺测出摆长缩短的长度△l,用上述测量的物理量,写出重力加速度的表达式g= .
12.(8分)如图甲所示,用“碰撞实验器”可以验证动量守恒定律,即研究两个小球在轨道水平部分碰撞前后的动量关系.
(1)图甲中O点是小球抛出点在地面上的垂直投影.实验时,先让入射球m1多次从斜轨上S位置静止释放,找到其平均落地点的位置P,测量平抛射程OP.然后,把被碰小球m2静置于轨道的水平部分,再将入射球m1从斜轨上S位置静止释放,与小球m2相碰,并多次重复.接下来要完成的必要步骤是 .(填选项前的符号)
A.用天平测量两个小球的质量m1、m2
B.测量小球m1开始释放高度h
C.测量抛出点距离地面的高度H
D.分别找到m1、m2相碰后平均落地点的位置M、N
E.测量平抛射程OM、ON
(2)经测定,m1=45.0g,m2=7.5g,小球落地点的平均位置距O点的距离如图乙所示.实验结果说明,碰撞前、后总动量的比值为 (用(1)中测量的量表示),代入数值求得这个比值为 .
(3)在上述实验中仅更换两个小球的材质,其他条件不变,可以使被碰小球做平抛运动的射程增大,请用(2)中已知的数据,计算出被碰小球m2平抛运动射程ON的最大值为 cm.
13.(8分)如图所示,一列简谐横波沿x轴传播,实线是这列波在t1=0时刻的波形,虚线是这列波在t2=0.5s时刻的波形,问:
(1)若这列波的波速大小为74m/s,求波传播的方向?
(2)若这列波的周期为T,且3T<t2﹣t1<4T,求这列波的波速是多大?
14.(10分)如图所示,横截面为四分之一圆的柱形玻璃砖放在水平面MN上,O点是圆心.一列与OA面等高的平行光束沿水平方向垂直射向玻璃砖的OA面,平行光束通过玻璃砖后在水平面MN上留下照亮的区域.已知玻璃砖的折射率为n(n<2),不考虑光在OA、OB面的反射.求:
(1)若在玻璃砖左侧竖直放置一遮光板,使水平面BN不被照亮,遮光板的最小高度是多少?
(2)撤去遮光板,从OA的中点射入的光,在MN上的P处留下一个光点,P点到O点的距离是多少?
15.(12分)如图所示,木板的质量为2m,长为L,静止在光滑的水平地面上,木板上下面均与地面平行.点A、B是木板的两个端点,点C是中点,AC段是光滑的,CB段是粗糙的,木板的A端放有一个质量为m的物块(可视为质点),现给木板一个瞬间冲量,使木板获得一个水平向右、大小为v0的速度,最终物块恰好滑到木板的B端与木板一起运动.求:
(1)物块滑到木板B点时木板的速度v;
(3)物块在AB段上滑行的时间t.
16.(14分)如图所示,A、B、C三个小物块放置在光滑水平面上,A紧靠在墙壁,A、B之间用轻弹簧连接,它们的质量分别为mA=m,mB=2m,mC=m.现使物块C获得水平向左的初速度v0,物块C与物块B发生碰撞并粘在一起不再分离.试求:
(1)物块A离开墙前,弹簧的最大弹性势能Em;
(2)物块A离开墙后,物块C的最小速度vmin.
参考答案与试题解析
一、选择题(本大题共10小题,每小题4分,共40分)
1.(4分)第一位提出“光本身也是一种电磁波”的科学家是( )
A.赫兹 B.法拉第 C.麦克斯韦 D.爱因斯坦
【解答】解:建立完整电磁场理论并首先预言电磁波存在的科学家是麦克斯韦,而赫兹证实了电磁波的存在,对于法拉第首次提出场的概念,并发现电磁感应现象,爱因斯坦的相对论。故C正确,ABD错误。
故选:C。
2.(4分)在光电效应实验中,用单色光照射光电管阴极,发生了光电效应.要使光电管中的电流增大,下列做法正确的是( )
A.保持入射光的频率不变,增加照射时间
B.保持入射光的频率不变,增大光的强度
C.保持入射光的强度不变,增加照射时间
D.保持入射光的强度不变,增大光的频率
【解答】解:A、保持入射光的频率不变,增加照射时间只能增加产生光电效应的时间,与饱和光电流无关。故A错误;
B、保持入射光的频率不变,光照强度增大,单位时间内照射到金属表面的光子数目增大,因此单位时间内产生的光电子数目增大,即饱和电流增大,故B正确;
C、结合B的方向可知,保持入射光的强度不变,不能判断出是否增大饱和光电流。故C错误;
D、保持入射光的强度不变,增大光的频率,则单个的光子的能量增大,所以单位时间内入射的光子的数目减少,所以单位时间内产生的光电子减少,所以饱和光电流减小。故D错误。
故选:B。
3.(4分)一束光由空气射向一块平行平面玻璃砖,折射后分为两束单色光a、b.下列判断正确的是( )
A.在玻璃砖中a光的速度大于b光的速度,射出玻璃砖后单色光a、b平行
B.在玻璃砖中a光的速度大于b光的速度,射出玻璃砖后单色光a、b不平行
C.在玻璃砖中a光的速度小于b光的速度,射出玻璃砖后单色光a、b平行
D.在玻璃砖中a光的速度小于b光的速度,射出玻璃砖后单色光a、b不平行
【解答】解:由光路图可知,b光的偏折程度较大,则b光的折射率大,根据v=知,b光在玻璃砖中传播的速度较小,光线在玻璃砖的上表面的折射角和下表面的入射角相等,根据光的可逆原理知,光线在下表面的折射角与上表面的入射角相等,可知射出玻璃砖后单色光a、b平行。故A正确,B、C、D错误。
故选:A。
4.(4分)如图所示是双缝干涉的实验装置,使用波长为600nm的橙色光照射单缝S,在光屏中央P处观察到亮条纹,在位于P的上方的P1处出现第一条亮纹中心,现换用波长为400nm的紫色光照射单缝S,则( )
A.P和P1处都为亮条纹
B.P和P1处都为暗条纹
C.P处是亮条纹,P1处是暗条纹
D.P处是暗条纹,P1处是亮条纹
【解答】解:缝S1、S2到光屏中央P点的距离相等,无论什么色光,其相干光的路程差均为0,故P处都是亮条纹。对于波长为600nm的橙色光,S1、S2到P1点的路程差恰好为橙色光的1个波长,则换用波长为400nm的紫色光时,S1、S2到P1点的路程差恰好为橙色光的1.5个波长,因此紫色光照射时在P1处是暗条纹。故C正确,A、B、D错误。
故选:C。
5.(4分)实验观察到,静止在匀强磁场中A点的原子核发生β衰变,衰变产生的新核与β粒子恰在纸面内做匀速圆周运动,粒子的轨迹如图所示,其中粒子在轨迹1是按顺时针方向运动.则( )
A.轨迹1是新核的,粒子在轨迹2是按顺时针方向活动
B.轨迹2是新核的,粒子在轨迹2是按顺时针方向运动
C.轨迹1是新核的,粒子在轨迹2是按逆时针方向运动
D.轨迹2是新核的,粒子在轨迹2是按逆时针方向运动
【解答】解:原子核发生β衰变时,根据动量守恒可知两粒子的速度方向相反,动量的方向相反,大小相等;
由半径公式r==(P是动量),分析得知,r与电荷量成反比,β粒子与新核的电量大小分别为e和ne(n为新核的电荷数),则β粒子与新核的半径之比为:ne:e=n:1。
所以半径比较大的轨迹1是衰变后β粒子的轨迹,轨迹2是新核的。
新核沿逆时针方向运动,在A点受到的洛伦兹力向左,由左手定则可知,磁场的方向向里。
由以上的分析可知,选项D正确,ABC错误。
故选:D。
6.(4分)如图所示,斜面体固定在水平地面上,斜面表面是光滑的且足够长.斜面顶端与自然长度为L的轻质弹簧相连,弹簧的另一端连接着物块m,当物块静止时,弹簧的伸长量为△l.压缩弹簧使弹簧长度为L时将物块由静止释放,则物块运动过程中,弹簧的最大伸长量为(运动过程中弹簧未超过弹性限度)
A.+2△l B.+△l C.L+2△l D.L+△l
【解答】解:由题,当物块静止时,弹簧的伸长量为△l;根据简谐运动的对称性,压缩弹簧使其长度为L时将物块由静止开始释放,故其振幅为:
A=L+△l
故其最大伸长量为:A+△l=L+2△l
故A正确,BCD错误
故选:A。
7.(4分)运动的原子核X放出α粒子后变成静止的原子核Y.已知原子核X、α粒子的质量分别是M、m,α粒子的动能为E,真空中的光速为c,α粒子的速度远小于光速.则在上述核反应中的质量亏损是( )
A. B.E C.E D.E
【解答】解:核反应中动量守恒,有:mvα=Mvx,
α粒子的动能为E=,
根据能量守恒得,,
由爱因斯坦质能方程得,△E=△mc2,
联立解得,故B正确,A、C、D错误。
故选:B。
8.(4分)氢原子基态的能量为E1=﹣13.6eV.大量氢原子处于某一激发态.由这些氢原子可能发出的所有光子中,频率最大的光子能量为﹣0.96E1,则( )
A.频率最小的光子能量为0.31eV
B.频率最小的光子能量为0.54eV
C.发出的光子具有4种不同的频率
D.发出的光子具有10种不同的频率
【解答】解:AB、氢原子基态的能量为E1=﹣13.6eV.大量氢原子处于某一激发态。
由这些氢原子可能发出的所有光子中,频率最大的光子能量为﹣0.96E1,即跃迁到最高能级能量E=0.04E1=﹣0.544eV,即处在n=5能级;
频率最小的光子的能量为△E′=﹣0.544eV﹣(﹣0.85eV)=0.31eV,故A正确,B错误;
CD、根据数学组合公式,=10,所以这些光子可具有10种不同的频率,故C错误,D正确。
故选:AD。
9.(4分)一列简谐横波在均匀介质中沿直线传播,P、Q是传播方向上相距10m的两个质点。波先传到P,当波传到Q开始计时,P、Q两质点的振动图象如图所示,则( )
A.质点Q开始振动的方向沿y轴正方向
B.该波从P点传到Q的最短时间为2s
C.该波波长的最大值为15m
D.该波的传播速度可能为m/s
【解答】解:A、根据y﹣t图象的斜率表示速度,知质点Q的起振方向沿y轴正方向,故A正确。
B、由题可知,简谐横波的传播方向从P到Q,由图可知,周期T=6s,质点Q的振动图象向左平移4s后与P点的振动图象重合,意味着Q点比P点振动最少滞后了4s,即P传到Q的时间△t至少为4s,由周期性可知,从P传到Q的时间△t=(4+nT)s,n=0、1、2、3…,即△t=4s,10s,16s…,不可能为2s,故B错误。
CD、由v==m/s,可知,当△t=4s,10s,16s…时,速度v可能为2.5m/s,1m/s,0.625m/s…,不可能为m/s。
由λ=vT,代入最大波速为2.5m/s时,求得波长的最大值为15m,故C正确,D错误。
故选:AC。
10.(4分)如图所示,光滑水平面上A、B两小球沿同一方向运动,A球的动量4kg m/s,B球的质量1kg,速度为6m/s,已知两球相碰后,A球的动量减为原来的一半,方向与原方向一致.则( )
A.A球的质量可能为0.4kg
B.A球的质量可能为0.5kg
C.A球碰撞后的速度不可能为4m/s
D.A球碰撞后的速度不可能为10m/s
【解答】解:AB、由题知,碰撞后A的动量为 p'A=2kg m/s,根据动量守恒定律有:pA+mBvB=p'A+mBv'B,解得 v'B=8.0m/s。
设A球质量为mA,A球能追上B球并与之碰撞,应满足 vA=>vB;碰撞后A球不可能运动到B球前方,故v′A=≤v′B;
碰撞过程系统的总动能不可能增加,故+mBvB2≤+mBvB′2
解得:kg≤mA≤kg(或0.25kg≤mA≤0.43kg),所以A球的质量可能为0.4kg,不可能为0.5kg,故A正确,B错误。
CD、碰撞后,B球的速度为v'B=8.0m/s,则A球碰撞后的速度不可能大于8.0m/s,所以A球碰撞后的速度不可能为10m/s。
若A球的质量为0.5kg,则碰撞前A球的速度为8m/s,碰撞后的速度为4m/s,碰撞前后A球动能的减少△EkA=﹣=﹣=12J
B球动能的增加量△EkB=mBvB′2﹣mBvB2=14J>△EkA,不可能,故CD正确。
故选:ACD。
二、非选择题(本大题共6小题,共60分)
11.(8分)利用单摆测量当地的重力加速度,如图甲所示,将长约为1m的细线上端固定在铁架台上,下端系一小钢球,就做成了单摆.
(1)用游标卡尺测量小钢球直径,示数如图乙所示,读数为 18.6 mm.
(2)图丙中的振动图象真实的描述了对摆长约为1m的单摆进行周期测量的三种操作过程,图中横坐标原点表示计时开始,A、B、C均为30次全振动的图象,已知sin5°=0.087,sin15°=0.26,这三种操作过程合乎实验要求且误差最小的是 A .
(3)某同学某次测量时误把30次全振动的时间当作31次全振动的时间,则这次测量得到的重力加速度值会 偏大 (填“偏大”或“不变”)
(4)实验时,由于仅有量程为20cm、精度为1mm的刻度尺,某同学先测出图甲单摆的周期T,然后将摆长缩短一些,再测出摆长改变后的单摆周期T,用刻度尺测出摆长缩短的长度△l,用上述测量的物理量,写出重力加速度的表达式g= .
【解答】解:(1)由图示游标卡尺可知,其示数为18mm+6×0.1mm=18.6mm.
(2)单摆的振动在摆角小于5°才能看作简谐振动,在测量周期时计时起点应该选择在平衡位置(速度大误差小).根据摆角估算振幅 A1=lsin5°=1×0.087m=0.087m=8.7cm≈8cm,AB振幅合理; A2=lsin15°=1×0.26m=0.26m=26cm,C振幅不合理,A中振动图象的计时起点在平衡位置是合理的,B中振动图象的计时起点在正的最大位置是不合理的,
故选:A;
(3)由单摆周期公式:T=2π可知重力加速度为:g=;误把30次全振动的时间当作31次全振动的时间,所测周期T偏小,则所测得的重力加速度值会偏大.
(4)由单摆周期公式得:T1=2π,T2=2π
解得:g=;
故答案为:(1)18.6;(2)A;(3)偏大;(4).
12.(8分)如图甲所示,用“碰撞实验器”可以验证动量守恒定律,即研究两个小球在轨道水平部分碰撞前后的动量关系.
(1)图甲中O点是小球抛出点在地面上的垂直投影.实验时,先让入射球m1多次从斜轨上S位置静止释放,找到其平均落地点的位置P,测量平抛射程OP.然后,把被碰小球m2静置于轨道的水平部分,再将入射球m1从斜轨上S位置静止释放,与小球m2相碰,并多次重复.接下来要完成的必要步骤是 ADE .(填选项前的符号)
A.用天平测量两个小球的质量m1、m2
B.测量小球m1开始释放高度h
C.测量抛出点距离地面的高度H
D.分别找到m1、m2相碰后平均落地点的位置M、N
E.测量平抛射程OM、ON
(2)经测定,m1=45.0g,m2=7.5g,小球落地点的平均位置距O点的距离如图乙所示.实验结果说明,碰撞前、后总动量的比值为 (用(1)中测量的量表示),代入数值求得这个比值为 1 .
(3)在上述实验中仅更换两个小球的材质,其他条件不变,可以使被碰小球做平抛运动的射程增大,请用(2)中已知的数据,计算出被碰小球m2平抛运动射程ON的最大值为 76.8 cm.
【解答】解:(1)A、小球的动量P=mv,实验需要用天平测量两个小球的质量m1、m2,故A正确;
B、只要每次从斜槽的同一位置由静止释放小球即可,不需要测量小球m1开始释放高度h,故B错误;
C、两球离开轨道后都做平抛运动,它们抛出点的高度相同,运动时间t相等,在表达式中t可以约去,实验不需要测量抛出点距离地面的高度H,故C错误;
D、小球离开轨道后做平抛运动,它们抛出点的高度相等,在空中的运动时间相等,可以用它们的水平位移代替初速度,实验需要分别找到m1、m2相碰后平均落地点的位置M、N,需要测量平抛射程OM、ON,故DE正确;
故选:ADE.
(2)由图示可知,P点是碰撞前入射球的落点,M、N分别是碰撞后入射球与被碰球的落点,
要验证动量守恒定律定律,即验证:m1v1=m1v2+m2v3,小球离开轨道后做平抛运动,
它们抛出点的高度相等,在空中的运动时间t相等,上式两边同时乘以t得:
m1v1t=m1v2t+m2v3t,得:m1OP=m1OM+m2ON,碰撞前后总动量的比值:
===1;
(3)两球发生弹性碰撞时,被碰小球获得速度最大,其水平射程最大,
以向右为正方向,由动量守恒定律得:m1v0=m1v1+m2v2,
由机械能守恒定律得:m1v02=m1v12+m2v22,
得动能守恒的表达式是:m1 OM2+m2 ON2=m1 OP2,
解得:v2=v0,
因此最大射程为:sm= OP=×44.80cm=76.8cm;
故答案为:(1)ADE;(2);1;(3)76.8.
13.(8分)如图所示,一列简谐横波沿x轴传播,实线是这列波在t1=0时刻的波形,虚线是这列波在t2=0.5s时刻的波形,问:
(1)若这列波的波速大小为74m/s,求波传播的方向?
(2)若这列波的周期为T,且3T<t2﹣t1<4T,求这列波的波速是多大?
【解答】解:(1)由图象可知:该波的波长 λ=8m。
若波速大小为74m/s,在△t=t2﹣t1=0.5s内波传播的距离为△x=v △t=74×0.5m=37m
因为=4
所以波沿x轴负方向传播;
(2)波在一个周期内传播的距离是一个波长,由3T<t2﹣t1<4T知,波传播距离为3λ<△x<4λ。
当波向x轴正方向传播时,波传播距离为:x=(3λ+3)m=(3×8+3)m=27m
波速为:v==m/s=54m/s;
当波向x轴负方向传播时,波传播距离为 x=(3λ+5)m=(3×8+5)m=29m
波速为:v═=m/s=58m/s。
答:(1)若这列波的波速大小为74m/s,波沿x轴负方向传播;
(2)当波向x轴正方向传播时,波速为54m/s;
当波向x轴负方向传播时,波速为58m/s。
14.(10分)如图所示,横截面为四分之一圆的柱形玻璃砖放在水平面MN上,O点是圆心.一列与OA面等高的平行光束沿水平方向垂直射向玻璃砖的OA面,平行光束通过玻璃砖后在水平面MN上留下照亮的区域.已知玻璃砖的折射率为n(n<2),不考虑光在OA、OB面的反射.求:
(1)若在玻璃砖左侧竖直放置一遮光板,使水平面BN不被照亮,遮光板的最小高度是多少?
(2)撤去遮光板,从OA的中点射入的光,在MN上的P处留下一个光点,P点到O点的距离是多少?
【解答】解:(1)如图1,当光线在AB面入射角大于临界角C时,将没有光线出射后射向BN平面,设遮光板高度为h,则
由折射定律有:sinC=,
由几何知识得h=RsinC
求得h=.
(2)如图2,当光在AB面中点入射时,入射角为30°,设P点到O点的距离为S,
由折射定律,
解得sinθ=,cosθ=,
在直角△OEP中,θ=30+γ
根据正弦定律有:,
因此S=R==,
代入θ的正弦值和余弦值,求得P点到O点的距离S=.
答:(1)遮光板的最小高度是;
(2)P点到O点的距离是.
15.(12分)如图所示,木板的质量为2m,长为L,静止在光滑的水平地面上,木板上下面均与地面平行.点A、B是木板的两个端点,点C是中点,AC段是光滑的,CB段是粗糙的,木板的A端放有一个质量为m的物块(可视为质点),现给木板一个瞬间冲量,使木板获得一个水平向右、大小为v0的速度,最终物块恰好滑到木板的B端与木板一起运动.求:
(1)物块滑到木板B点时木板的速度v;
(3)物块在AB段上滑行的时间t.
【解答】解:(1)在运动过程中,木板和物块组成的系统动量守恒,取向右为正方向,由动量守恒定律得:
2mv0=(2m+m)v
解得:v=
(2)设物块在AC段滑行时间为t1,在CB段滑行时间为t2,则有:
=v0t1.
=﹣.
解得:t=t1+t2=
答:(1)物块滑到木板B点时木板的速度v是;
(2)物块在AB段上滑行的时间t是.
16.(14分)如图所示,A、B、C三个小物块放置在光滑水平面上,A紧靠在墙壁,A、B之间用轻弹簧连接,它们的质量分别为mA=m,mB=2m,mC=m.现使物块C获得水平向左的初速度v0,物块C与物块B发生碰撞并粘在一起不再分离.试求:
(1)物块A离开墙前,弹簧的最大弹性势能Em;
(2)物块A离开墙后,物块C的最小速度vmin.
【解答】解:(1)设物块C与B发生碰撞粘在一起时的速度为v.C、B碰撞过程,选取向左为正方向,根据动量守恒定律得:
mcv0=(mc+mB)v
得:v=v0.
当C与B一起压缩弹簧至速度为零时弹簧的弹性势能最大.以B、C和弹簧组成的系统为研究对象,根据机械能守恒定律有:
Em=(mc+mB)2.
联立以上两式解得:Em=.
(2)在A离开墙壁时,弹簧第一次恢复原长,B、C以速度v向右运动;
在A离开墙壁后,由于弹簧的作用,A的速度逐渐增大,B、C的速度逐渐减小,当弹簧再次恢复原长时,B与C的速度最小.设B与C的速度最小时A的速度为vA.
选取向右为正方向,由A、B、C三物体组成系统动量守恒得:
(mB+mC)v=mAvA+(mB+mC)vmin
又由能量守恒定律有:(mB+mC)v2=mAvA2+(mB+mC)vmin2
联立解得:vmin=
答:(1)A离开墙前,弹簧的最大弹性势能Em为.
(2)物块A离开墙后,物块C的最小速度vmin为.
同课章节目录
