沪科版数学八年级上册 11.2 图形在坐标系中的平移(2) 课件(共18张PPT)
文档属性
| 名称 | 沪科版数学八年级上册 11.2 图形在坐标系中的平移(2) 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 334.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-31 12:57:26 | ||
图片预览




文档简介
(共18张PPT)
11.2 图形在坐标系中的平移
1
2
3
-1
-2
-3
y
x
1
2
3
-1
-2
-3
-4
O
在平面内有公共原点而且互相垂直的两条数轴,构成了平面直角坐标系.
x
O
1
2
3
-1
-2
-3
1
2
-1
-2
-3
y
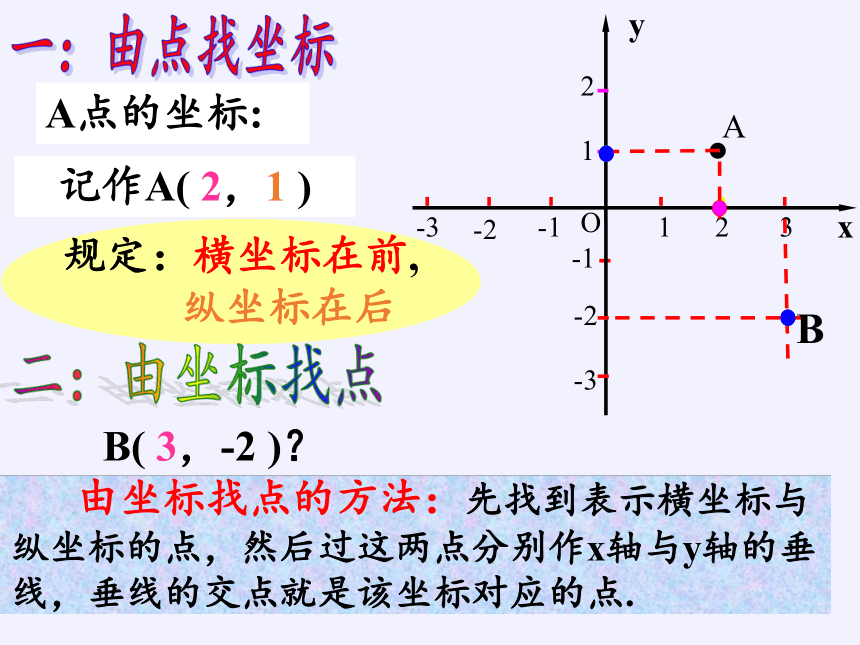
A
A点的坐标:
记作A( 2,1 )
一:由点找坐标
规定:横坐标在前,
纵坐标在后
二:由坐标找点
B( 3,-2 )?
由坐标找点的方法:先找到表示横坐标与
纵坐标的点,然后过这两点分别作x轴与y轴的垂
线,垂线的交点就是该坐标对应的点.
B
第四象限
1
2
3
-1
-2
-3
y
x
1
2
3
-1
-2
-3
-4
O
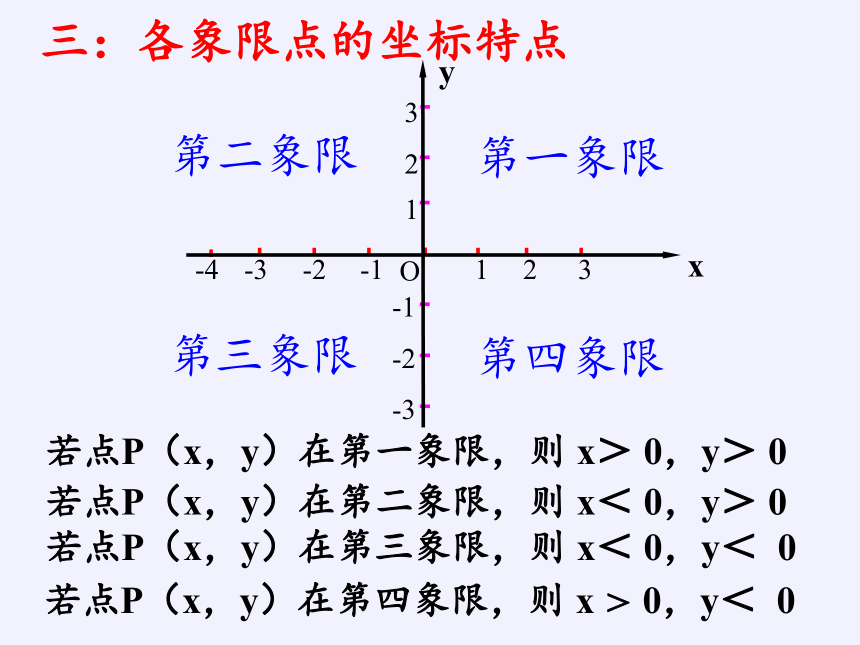
若点P(x,y)在第一象限,则 x> 0,y> 0
若点P(x,y)在第二象限,则 x< 0,y> 0
若点P(x,y)在第三象限,则 x< 0,y< 0
若点P(x,y)在第四象限,则 x > 0,y< 0
三:各象限点的坐标特点
第一象限
第三象限
第二象限
第四象限
1
2
3
-1
-2
-3
y
x
1
2
3
-1
-2
-3
-4
O
第一象限
第三象限
第二象限
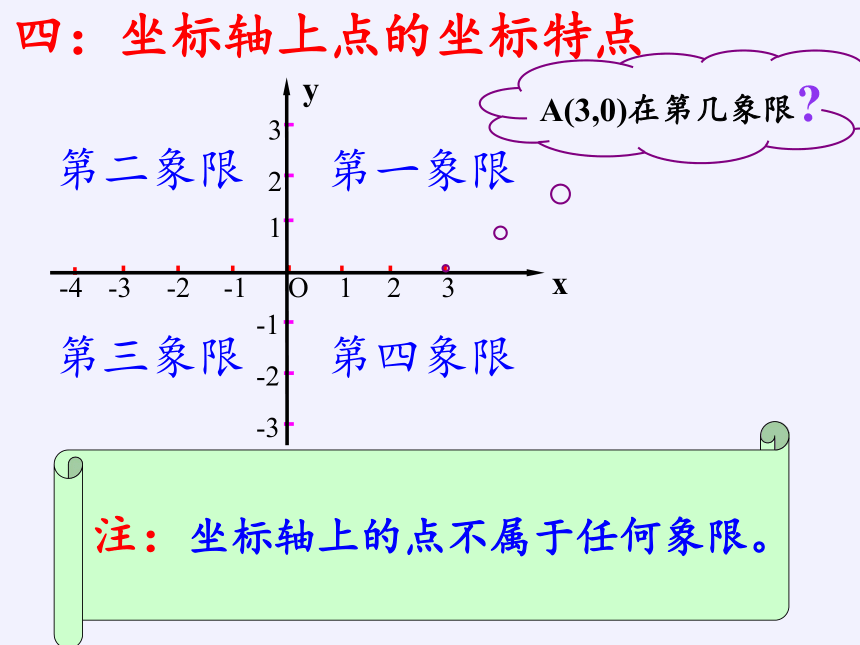
A(3,0)在第几象限
注:坐标轴上的点不属于任何象限。
四:坐标轴上点的坐标特点
四:坐标轴上点的坐标特点
1.点P(m+2,m-1)在x轴上,则点P的坐标是 .
( 3, 0 )
2.点P(m+2,m-1)在y轴上,则点P的坐标是 .
( 0, -3 )
3. 点P(x,y)满足 xy=0, 则点P在 .
x 轴上 或 y 轴上
4.若 ,则点p(x,y)位于 __
y轴(除(0,0))上
注意:1. x轴上的点的纵坐标为0,表示为(x,0),
2. y轴上的点的横坐标为0, 表示为(0,y)。
原点(0,0)既在x轴上,又在y轴上。
(2). 若AB∥ y 轴,
则A( m, y1 ), B( m, y2 )
(1). 若AB∥ x 轴,
则A( x1, n ), B( x2, n )
五:两点连线与坐标轴平行
1. 已知点A(m,-2),点B(3,m-1),且直线AB∥x轴,则m的值为 。
-1
2. 已知点A(m,-2),点B(3,m-1),且直线AB∥y轴,则m的值为 。
3
已知点A(10,5),B(50,5),则直线AB的位置特点是( )
A.与x轴平行 B.与y轴平行
C.与x轴相交,但不垂直 D.与y轴相交,但不垂直
A
1. 点( x, y )到 x 轴的距离是
2. 点( x, y )到 y 轴的距离是
1.若点A的坐标是(- 3, 5),则它到x轴的距离是 ,到y轴的距离是 .
5
3
2.若点B在x轴上方,y轴右侧,并且到 x 轴、y 轴距离分别是2、4个单位长度,则点B的坐标是 .
(4,2)
3.点P到x轴、y轴的距离分别是2,1,则点P的坐标可能为 .
(1,2)、(1,-2)、(-1,2)、(-1,-2)
六:点到坐标轴的距离
(1)点(a, b )关于X轴的对称点是( )
a, -b
- a, b
-a, -b
(2)点(a, b )关于Y 轴的对称点是( )
(3)点(a, b )关于原点的对称点是( )
七:关于坐标轴、原点的对称点
1.已知A、B关于x轴对称,A点的坐标为(3,2),则B
的坐标为 .
(3,-2)
2.若点A(m, -2), B(1, n)关于y轴对称, m= ,n= .
-1
-2
3.已知点A(3a -1,1+ a)在第一象限的角平分线上,试求A关于原点的对称点的坐标.
解析:由3a -1 = 1+ a得a =1,则A(1,1)所以B(-1 ,-1)
向左平移
a个单位
向下平移
个单位
b
向上平移
个单位
b
向右平移
a个单位
八:平 移
P(x, y)
P(x, y-b)
P(x, y+b)
P(x-a, y)
P(x+a, y)
九:平面直角坐标系的应用
1. 确定点的位置
2. 求平面图形的面积
3. 用坐标表示平移
用直角坐标来表述物体位置
1、图是某乡镇的示意图.试建立直角坐标系,用坐标表示各地的位置:
(1,3)
(3,3)
(-1,1)
(-3,-1)
(2,-2)
(-3,-4)
(3,-3)
已知点A(6,2),B(2,-4),求△AOB的面积(O为坐标原点).
2、
C
D
x
y
O
2
4
2
4
-2
-4
-2
-4
A
B
6
解析:S△AOB = S梯形ABCD - S△AOD - S△COB = 14
补
形
3.如图,四边形ABCD各个顶点的坐标分别为(– 2,8),(– 11,6),(– 14,0),(0,0).
(1)确定这个四边形的面积,你是怎么做的
(2)如果把原来ABCD各个顶点纵坐标保持不变,横坐标 增加2,所得的四边形面积又是多少?
F
E
S=80平 方单位
S=80平方单位
分
割
4、在平面直角坐标系中,点M(1,2)可由点N(2,0)怎样平移得到,写出简要过程.
5、三角形ABC中BC边上的中点为M,在把三角形ABC向左平移2个单位,再向上平移3个单位后,得到三角形A1B1C1的B1C1边上中点M1此时的坐标为(-1,0),则M点坐标为 .
解析:由点N(2,0)向左平移1个单位再向上平移2个单位得到点M(1,2).
(1,-3)
课后思考
完成下列各题,你能得到什么结论
3.已知点M(a+1,3a-5)在两坐标轴夹角的平分线上,试求M的坐标。
2.已知点A(2a+1,2+a)在第二象限的角平分线上,试求A的坐标。
1.已知点A(2,y ),点B(x ,5 ),点A、B在一、三象限的角平分线上, 则x =____,y =____;
(1). 若点P在第一、三象限角的平分线上,则P( m, m ).
(2). 若点P在第二、四象限角的平分线上则P( m, -m ).
思考
3.已知点M(a+1,3a-5)在两坐标轴夹角的平分线上,试求M的坐标。
2.已知点A(2a+1,2+a)在第二象限的平分线上,试求A的坐标。
1.已知点A(2,y ),点B(x ,5 ),点A、B在一、三象限的角平分线上, 则x =____,y =____;
解析:由(2a+1)+(2+a)=0得a=-1,则A(-1,1)
谢 谢
11.2 图形在坐标系中的平移
1
2
3
-1
-2
-3
y
x
1
2
3
-1
-2
-3
-4
O
在平面内有公共原点而且互相垂直的两条数轴,构成了平面直角坐标系.
x
O
1
2
3
-1
-2
-3
1
2
-1
-2
-3
y
A
A点的坐标:
记作A( 2,1 )
一:由点找坐标
规定:横坐标在前,
纵坐标在后
二:由坐标找点
B( 3,-2 )?
由坐标找点的方法:先找到表示横坐标与
纵坐标的点,然后过这两点分别作x轴与y轴的垂
线,垂线的交点就是该坐标对应的点.
B
第四象限
1
2
3
-1
-2
-3
y
x
1
2
3
-1
-2
-3
-4
O
若点P(x,y)在第一象限,则 x> 0,y> 0
若点P(x,y)在第二象限,则 x< 0,y> 0
若点P(x,y)在第三象限,则 x< 0,y< 0
若点P(x,y)在第四象限,则 x > 0,y< 0
三:各象限点的坐标特点
第一象限
第三象限
第二象限
第四象限
1
2
3
-1
-2
-3
y
x
1
2
3
-1
-2
-3
-4
O
第一象限
第三象限
第二象限
A(3,0)在第几象限
注:坐标轴上的点不属于任何象限。
四:坐标轴上点的坐标特点
四:坐标轴上点的坐标特点
1.点P(m+2,m-1)在x轴上,则点P的坐标是 .
( 3, 0 )
2.点P(m+2,m-1)在y轴上,则点P的坐标是 .
( 0, -3 )
3. 点P(x,y)满足 xy=0, 则点P在 .
x 轴上 或 y 轴上
4.若 ,则点p(x,y)位于 __
y轴(除(0,0))上
注意:1. x轴上的点的纵坐标为0,表示为(x,0),
2. y轴上的点的横坐标为0, 表示为(0,y)。
原点(0,0)既在x轴上,又在y轴上。
(2). 若AB∥ y 轴,
则A( m, y1 ), B( m, y2 )
(1). 若AB∥ x 轴,
则A( x1, n ), B( x2, n )
五:两点连线与坐标轴平行
1. 已知点A(m,-2),点B(3,m-1),且直线AB∥x轴,则m的值为 。
-1
2. 已知点A(m,-2),点B(3,m-1),且直线AB∥y轴,则m的值为 。
3
已知点A(10,5),B(50,5),则直线AB的位置特点是( )
A.与x轴平行 B.与y轴平行
C.与x轴相交,但不垂直 D.与y轴相交,但不垂直
A
1. 点( x, y )到 x 轴的距离是
2. 点( x, y )到 y 轴的距离是
1.若点A的坐标是(- 3, 5),则它到x轴的距离是 ,到y轴的距离是 .
5
3
2.若点B在x轴上方,y轴右侧,并且到 x 轴、y 轴距离分别是2、4个单位长度,则点B的坐标是 .
(4,2)
3.点P到x轴、y轴的距离分别是2,1,则点P的坐标可能为 .
(1,2)、(1,-2)、(-1,2)、(-1,-2)
六:点到坐标轴的距离
(1)点(a, b )关于X轴的对称点是( )
a, -b
- a, b
-a, -b
(2)点(a, b )关于Y 轴的对称点是( )
(3)点(a, b )关于原点的对称点是( )
七:关于坐标轴、原点的对称点
1.已知A、B关于x轴对称,A点的坐标为(3,2),则B
的坐标为 .
(3,-2)
2.若点A(m, -2), B(1, n)关于y轴对称, m= ,n= .
-1
-2
3.已知点A(3a -1,1+ a)在第一象限的角平分线上,试求A关于原点的对称点的坐标.
解析:由3a -1 = 1+ a得a =1,则A(1,1)所以B(-1 ,-1)
向左平移
a个单位
向下平移
个单位
b
向上平移
个单位
b
向右平移
a个单位
八:平 移
P(x, y)
P(x, y-b)
P(x, y+b)
P(x-a, y)
P(x+a, y)
九:平面直角坐标系的应用
1. 确定点的位置
2. 求平面图形的面积
3. 用坐标表示平移
用直角坐标来表述物体位置
1、图是某乡镇的示意图.试建立直角坐标系,用坐标表示各地的位置:
(1,3)
(3,3)
(-1,1)
(-3,-1)
(2,-2)
(-3,-4)
(3,-3)
已知点A(6,2),B(2,-4),求△AOB的面积(O为坐标原点).
2、
C
D
x
y
O
2
4
2
4
-2
-4
-2
-4
A
B
6
解析:S△AOB = S梯形ABCD - S△AOD - S△COB = 14
补
形
3.如图,四边形ABCD各个顶点的坐标分别为(– 2,8),(– 11,6),(– 14,0),(0,0).
(1)确定这个四边形的面积,你是怎么做的
(2)如果把原来ABCD各个顶点纵坐标保持不变,横坐标 增加2,所得的四边形面积又是多少?
F
E
S=80平 方单位
S=80平方单位
分
割
4、在平面直角坐标系中,点M(1,2)可由点N(2,0)怎样平移得到,写出简要过程.
5、三角形ABC中BC边上的中点为M,在把三角形ABC向左平移2个单位,再向上平移3个单位后,得到三角形A1B1C1的B1C1边上中点M1此时的坐标为(-1,0),则M点坐标为 .
解析:由点N(2,0)向左平移1个单位再向上平移2个单位得到点M(1,2).
(1,-3)
课后思考
完成下列各题,你能得到什么结论
3.已知点M(a+1,3a-5)在两坐标轴夹角的平分线上,试求M的坐标。
2.已知点A(2a+1,2+a)在第二象限的角平分线上,试求A的坐标。
1.已知点A(2,y ),点B(x ,5 ),点A、B在一、三象限的角平分线上, 则x =____,y =____;
(1). 若点P在第一、三象限角的平分线上,则P( m, m ).
(2). 若点P在第二、四象限角的平分线上则P( m, -m ).
思考
3.已知点M(a+1,3a-5)在两坐标轴夹角的平分线上,试求M的坐标。
2.已知点A(2a+1,2+a)在第二象限的平分线上,试求A的坐标。
1.已知点A(2,y ),点B(x ,5 ),点A、B在一、三象限的角平分线上, 则x =____,y =____;
解析:由(2a+1)+(2+a)=0得a=-1,则A(-1,1)
谢 谢
