沪科版数学八年级上册 14.2 全等三角形判定复习 课件(共17张PPT)
文档属性
| 名称 | 沪科版数学八年级上册 14.2 全等三角形判定复习 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 203.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-31 13:03:15 | ||
图片预览






文档简介
(共17张PPT)
全等三角形判定复习
一般三角形 全等的条件:
1.定义(重合)法;
2.SSS;
3.SAS;
4.ASA;
5.AAS.
直角三角形 全等特有的条件:
HL.
包括直角三角形
不包括其它形状的三角形
解题中常用的4种方法
三角形全等的证题思路:
①
②
③
1.证明两个三角形全等,要结合题目的条件和结论,选择恰当的判定方法
2.全等三角形,是证明两条线段或两个角相等的重要方法之一,证明时
①要观察待证的线段或角,在哪两个可能全等的三角形中。
②分析要证两个三角形全等,已有什么条件,还缺什么条件。
③有公共边的,公共边一定是对应边, 有公共角的,公共角一定是对应角,有对顶角,对顶角也是对应角
总之,证明过程中能用简单方法的就不要绕弯路。
例题讲解
例1:如图,D在AB上,E在AC上,且∠B =∠C,那么补充下列一具条件后,仍无法判定△ABE≌△ACD的是( )
A.AD=AEB. ∠AEB=∠ADC
C.BE=CD D.AB=AC
例题讲解
例2:已知:如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于O点,∠1=∠2,图中全等的三角形共有( )
A.1对 B.2对 C.3对 D.4对
例题讲解
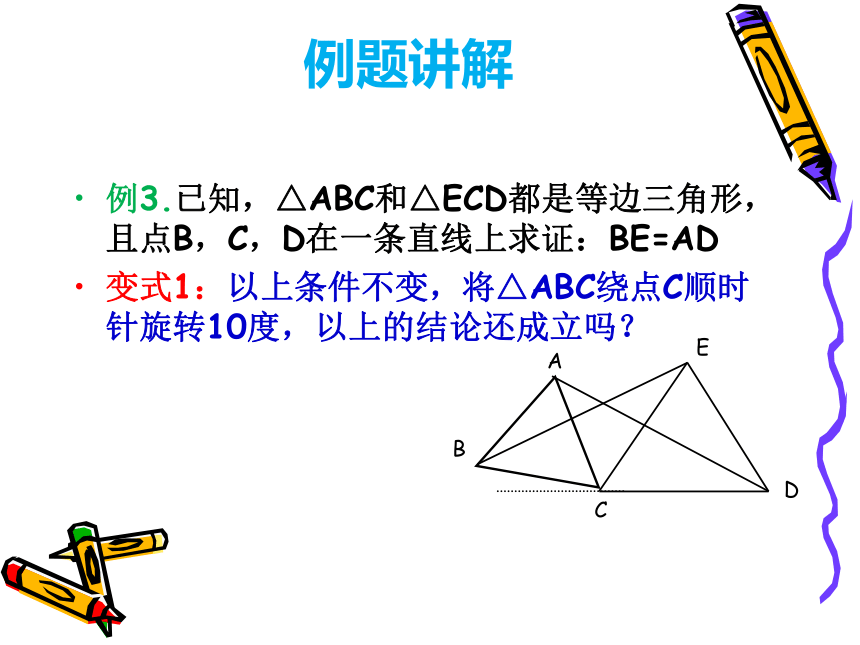
例3.已知,△ABC和△ECD都是等边三角形,且点B,C,D在一条直线上求证:BE=AD
变式1:以上条件不变,将△ABC绕点C顺时针旋转10度,以上的结论还成立吗?
E
D
C
A
B
例3变式2
例4.已知,△ABC和△ECD都是等边三角形,且点B,C,D在一条直线上求证:BE=AD
变式:以上条件不变,将△ABC绕点C顺时针旋转60度,以上的结论还成立吗?
E
D
C
A
B
例3变式3
例5.已知,△ABC和△ECD都是等边三角形,当△ABC绕点C顺时针旋转ɑ时,连接BE,DA;结论BE=AD还成立吗?若成立请加以证明。
E
D
C
A
B
E
D
C
A
B
例3变式4
引申:例6.已知,△ABC和△ECD都是等边三角形,且点B,C,D在一条直线上,AC与BE相交于M,CE与AD相交于N,试判定△CMN的形状
E
D
C
A
B
M
N
解:△CMN是等边三角形
证明:
(1)先证∠ACE=60°
(2)证明△BCE≌△ACD→∠BEC=∠ADC
(3)在证△MCE≌△NCD→CM=CN
课堂练习
1.已知BD=CD,∠ABD=∠ACD,DE、DF分别垂直于AB及AC交延长线于E、F,求证:DE=DF
┏
┏
课堂练习
2.点A、F、E、C在同一直线上,AF=CE,BE = DF,BE∥DF,求证:AB∥CD。
课堂练习
3.已知点A,E,F,C在同一条直线上,且AE=CF,过E F两点分别作DE⊥AC,BF⊥AC,且AB=CD,(1)求证:BD平分 EF(2)若将△DEC的边EC沿AC方向移动,变化为2时,其余条件不变,上述结论是否成立,说明理由
A
D
B
C
E
F
G
图1
A
D
B
C
E
F
G
图2
课堂练习
4.如图在三角形ABC中,BC上的高为AD,且∠B=2∠C
求证:CD=AB+BD
A
C
D
B
课堂练习
5.如图:在四边形ABCD中,点E在边CD上,连接AE、BE并延长AE交BC的延长线于点F,给出下列5个关系式::①AD∥BC,②,DE=EC③∠1=∠2,④∠3=∠4,⑤AD+BC=AB。将其中三个关系式作为已知,另外两个作为结论,构成正确的命题。请用序号写出两个正确的命题:(书写形式:如果……那么……)(1) ;(2) ;
知识小结
1、全等三角形的概念——
2、全等三角形的性质——
3、全等三角形的判定方法
(SSS)
(SAS)
(ASA)
(AAS)
(HL)
能够重合的三角形
对应边相等、对应角相等
三角形全等判定方法的思路:
已知条件 可选择的判定方法
SAS
ASA
AAS
SAS
AAS
ASA
SSS
一边一角对应相等
两组角对应相等
两组边对应相等
判定思路小结
HL
全等三角形判定复习
一般三角形 全等的条件:
1.定义(重合)法;
2.SSS;
3.SAS;
4.ASA;
5.AAS.
直角三角形 全等特有的条件:
HL.
包括直角三角形
不包括其它形状的三角形
解题中常用的4种方法
三角形全等的证题思路:
①
②
③
1.证明两个三角形全等,要结合题目的条件和结论,选择恰当的判定方法
2.全等三角形,是证明两条线段或两个角相等的重要方法之一,证明时
①要观察待证的线段或角,在哪两个可能全等的三角形中。
②分析要证两个三角形全等,已有什么条件,还缺什么条件。
③有公共边的,公共边一定是对应边, 有公共角的,公共角一定是对应角,有对顶角,对顶角也是对应角
总之,证明过程中能用简单方法的就不要绕弯路。
例题讲解
例1:如图,D在AB上,E在AC上,且∠B =∠C,那么补充下列一具条件后,仍无法判定△ABE≌△ACD的是( )
A.AD=AEB. ∠AEB=∠ADC
C.BE=CD D.AB=AC
例题讲解
例2:已知:如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于O点,∠1=∠2,图中全等的三角形共有( )
A.1对 B.2对 C.3对 D.4对
例题讲解
例3.已知,△ABC和△ECD都是等边三角形,且点B,C,D在一条直线上求证:BE=AD
变式1:以上条件不变,将△ABC绕点C顺时针旋转10度,以上的结论还成立吗?
E
D
C
A
B
例3变式2
例4.已知,△ABC和△ECD都是等边三角形,且点B,C,D在一条直线上求证:BE=AD
变式:以上条件不变,将△ABC绕点C顺时针旋转60度,以上的结论还成立吗?
E
D
C
A
B
例3变式3
例5.已知,△ABC和△ECD都是等边三角形,当△ABC绕点C顺时针旋转ɑ时,连接BE,DA;结论BE=AD还成立吗?若成立请加以证明。
E
D
C
A
B
E
D
C
A
B
例3变式4
引申:例6.已知,△ABC和△ECD都是等边三角形,且点B,C,D在一条直线上,AC与BE相交于M,CE与AD相交于N,试判定△CMN的形状
E
D
C
A
B
M
N
解:△CMN是等边三角形
证明:
(1)先证∠ACE=60°
(2)证明△BCE≌△ACD→∠BEC=∠ADC
(3)在证△MCE≌△NCD→CM=CN
课堂练习
1.已知BD=CD,∠ABD=∠ACD,DE、DF分别垂直于AB及AC交延长线于E、F,求证:DE=DF
┏
┏
课堂练习
2.点A、F、E、C在同一直线上,AF=CE,BE = DF,BE∥DF,求证:AB∥CD。
课堂练习
3.已知点A,E,F,C在同一条直线上,且AE=CF,过E F两点分别作DE⊥AC,BF⊥AC,且AB=CD,(1)求证:BD平分 EF(2)若将△DEC的边EC沿AC方向移动,变化为2时,其余条件不变,上述结论是否成立,说明理由
A
D
B
C
E
F
G
图1
A
D
B
C
E
F
G
图2
课堂练习
4.如图在三角形ABC中,BC上的高为AD,且∠B=2∠C
求证:CD=AB+BD
A
C
D
B
课堂练习
5.如图:在四边形ABCD中,点E在边CD上,连接AE、BE并延长AE交BC的延长线于点F,给出下列5个关系式::①AD∥BC,②,DE=EC③∠1=∠2,④∠3=∠4,⑤AD+BC=AB。将其中三个关系式作为已知,另外两个作为结论,构成正确的命题。请用序号写出两个正确的命题:(书写形式:如果……那么……)(1) ;(2) ;
知识小结
1、全等三角形的概念——
2、全等三角形的性质——
3、全等三角形的判定方法
(SSS)
(SAS)
(ASA)
(AAS)
(HL)
能够重合的三角形
对应边相等、对应角相等
三角形全等判定方法的思路:
已知条件 可选择的判定方法
SAS
ASA
AAS
SAS
AAS
ASA
SSS
一边一角对应相等
两组角对应相等
两组边对应相等
判定思路小结
HL
