沪科版数学九年级上册 22.3 相似三角形的性质 课件(共18张PPT)
文档属性
| 名称 | 沪科版数学九年级上册 22.3 相似三角形的性质 课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 242.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-31 17:47:17 | ||
图片预览




文档简介
(共18张PPT)
22.3 相似三角形的性质
1、相似三角形有哪些性质?
2、相似三角形有哪些判定方法?
对应线段成比例,对应角相等。
⑴ 定义 对应角相等,对应边成比例的两个三角形相似。
⑵ 判定定理1 两角对应相等的两个三角形相似。
⑶ 判定定理2 两边对应成比例且夹角相等的两个三角形相似。
⑷ 判定定理3 三边对应成比例的两个三角形相似。
?
?
温故知新
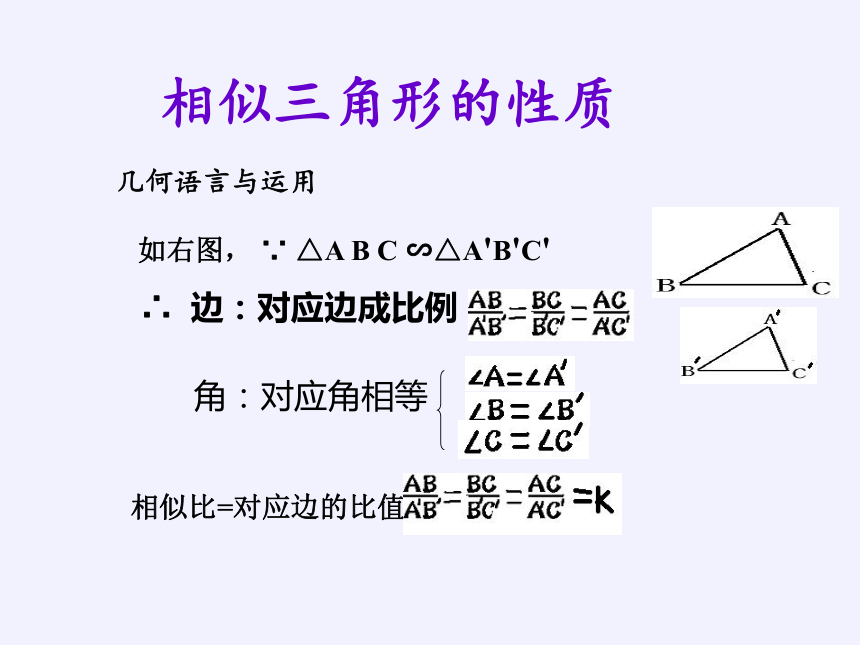
相似三角形的性质
几何语言与运用
角:对应角相等
∴ 边:对应边成比例
相似比=对应边的比值=
如右图, ∵ △A B C ∽△A'B'C'
全等三角形中对应边上的高、中线、对应角的平分线相等。
问:那么相似三角形中的这些对应线段又有哪些性质呢?
想一想:
如左下图,已知:△ ABC ∽ △ A'B'C',它们的相似比为k,AD、 A'D'是对应高。求证:
A
B D C
A'
B' D' C'
证明:
∵ △ ABC∽ △ A'B'C'
∴∠B= ∠B'
∵AD、 A'D'分别为BC 、B'C'边上的高
∴∠ADB= ∠A'D'B'=90°
∴ △ ABD∽ △ A'B'D'
∴AD:A'D'=AB:A'B'=k
结论1 相似三角形对应高的比等于相似比。
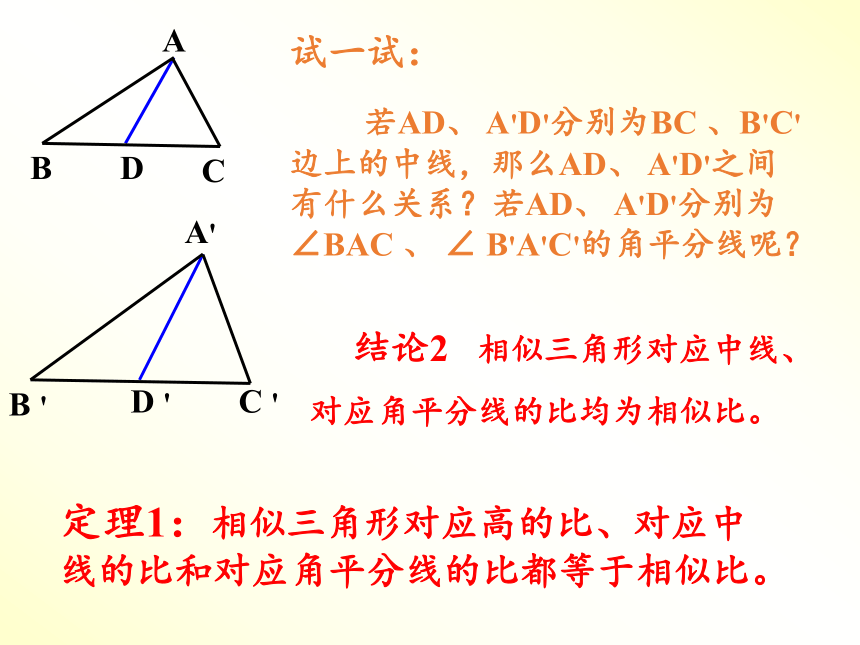
试一试:
若AD、 A'D'分别为BC 、B'C'边上的中线,那么AD、 A'D'之间有什么关系?若AD、 A'D'分别为∠BAC 、 ∠ B'A'C'的角平分线呢?
结论2 相似三角形对应中线、
对应角平分线的比均为相似比。
A
B
C
D
B '
C '
A'
D '
定理1:相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比。
A
B
C
B '
C '
A'
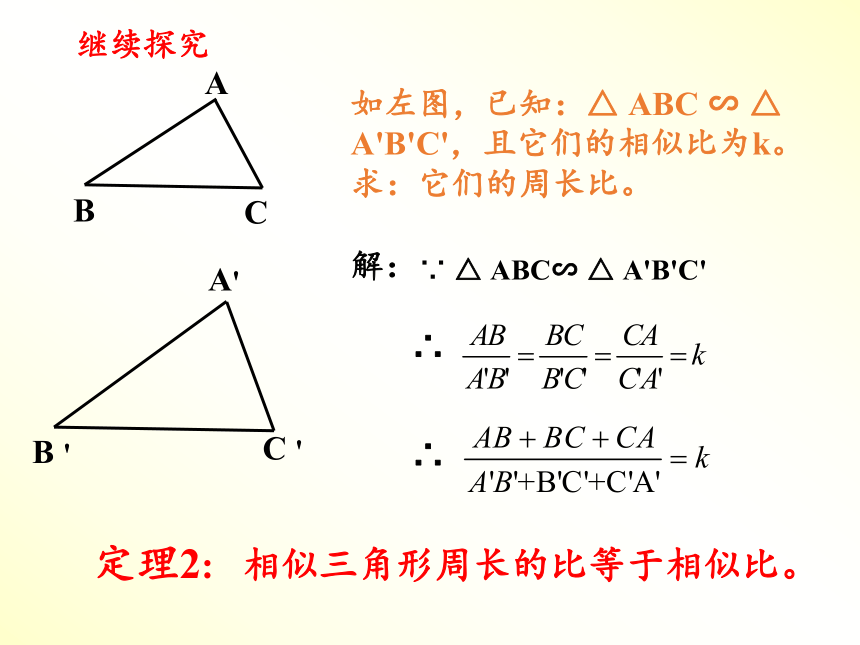
如左图,已知:△ ABC ∽ △ A'B'C',且它们的相似比为k。求:它们的周长比。
解:
∵ △ ABC∽ △ A'B'C'
∴
∴
定理2: 相似三角形周长的比等于相似比。
继续探究
做一做
如下图⑴、⑵、⑶分别是边长为1、2、3的等边三角形,它们都相似。
⑴
⑵
⑶
⑵与⑴的相似比=( )
⑵与⑴的面积比=( )
⑶与⑴的相似比=( )
⑶与⑴的面积比=( )
由此我们可以得到什么结论?
对等边三角形而言,面积比=相似比的平方。
2:1
4:1
3:1
9:1
动动你聪明的
脑子,想一想
上述结论是否适用于一般的相似三角形?
A
B
C
A′
B′
C′
D
D′
证明:
∽ △
△
分别过A、A′,
作AD⊥BC于D,
∵
∴
∴
∴
定理3 相似三角形面积的比等于相似比的平方。
例1:如图,一块铁皮呈锐角三角形,它的边BC=80cm,高AD=60cm。要把它加工成矩形零件,使矩形的长、宽之比为2:1,并且矩形长的一边位于边BC上,另两个顶点分别在边AB、AC上。求这个矩形零件的长与宽。
A
B
C
┐
D
解:如图,矩形PQRS为加工成的矩形零件,边SR在BC上,顶点P、Q分别在AB、AC上, △ ABC的高AD交PQ于点E。设PS为xcm,则PQ为2xcm。
∵
PQ//BC
∴
△ APQ∽ △ ABC
∴
即
解方程,得
因而,这个矩形零件的长是48cm,宽是24cm.
P
Q
S
R
E
请回答
1、若两个三角形的相似比为3:5,则这两个三角形对应高的比为( ),对应角平分线的比为( ),周长之比为( ),对应中线之比为( )。
2、把一个三角形改成和它相似的三角形,如果面积扩大为原来的100倍,那么边长扩大为原来的几倍?
3、已知两个等边三角形的边长之比为2:3,且它们的面积之和为26cm2,则较小的等边三角形的面积为多少?
3:5
3:5
3:5
10倍
8cm2
3:5
小试牛刀:
小试牛刀
4、顺次连接三角形三边中点所得的三角形与原三
角形周长比是_____,面积比是
1/2
1/4
再接再厉
5,如图DE∥BC,EF∥AB,S△ADE=25,S△CEF=36.
求△ABC的面积.
A
B
C
D
E
F
25
36
解:∵DE∥BC,EF∥AB
∴∠A=∠CEF,∠AED=∠C
∴△ADE∽△EFC
∴
∵DE∥BC
∴△ADE∽△ABC
∵ S△ADE=25
∴S △ABC=121
∴
∴
∴
E
A
B
C
.
6、如图, 在△ABC中,AB=5,AC=4,E是AB上一点,AE=2, 在AC上取一点F,使以A、E、F为顶点的三角形与 △ABC相似,那么AF=________
F2
F1
再接再厉
D
Q
A
B
C
P
如图, 边长为4的正方形ABCD中, P是边BC上的一点, QP⊥AP
交 DC于Q, 设
BP= x, △ADQ的面积为y.
(1) 求y与x之间的函数关系式,并求自变量x的取值范围;
(2) 问P点在何位置时,△ADQ的面积最小 最小面积是多少
相似与函数的相关习题
对于例1,要使得内接矩形PQRS的面积最大,此时该矩形的长与宽各是多少?
拓展练习
P
Q
S
R
E
A
B
C
┐
D
1、相似三角形对应边成____,对应角______.
2、相似三角形对应边上的高、对应边上的中线、
对应角平分线的比都等于________.
3、相似三角形周长的比等于________,
相似三角形面积的比等于______________.
课堂小结
相似比的平方
相似三角形的性质
比例
相等
相似比
相似比
谢 谢
22.3 相似三角形的性质
1、相似三角形有哪些性质?
2、相似三角形有哪些判定方法?
对应线段成比例,对应角相等。
⑴ 定义 对应角相等,对应边成比例的两个三角形相似。
⑵ 判定定理1 两角对应相等的两个三角形相似。
⑶ 判定定理2 两边对应成比例且夹角相等的两个三角形相似。
⑷ 判定定理3 三边对应成比例的两个三角形相似。
?
?
温故知新
相似三角形的性质
几何语言与运用
角:对应角相等
∴ 边:对应边成比例
相似比=对应边的比值=
如右图, ∵ △A B C ∽△A'B'C'
全等三角形中对应边上的高、中线、对应角的平分线相等。
问:那么相似三角形中的这些对应线段又有哪些性质呢?
想一想:
如左下图,已知:△ ABC ∽ △ A'B'C',它们的相似比为k,AD、 A'D'是对应高。求证:
A
B D C
A'
B' D' C'
证明:
∵ △ ABC∽ △ A'B'C'
∴∠B= ∠B'
∵AD、 A'D'分别为BC 、B'C'边上的高
∴∠ADB= ∠A'D'B'=90°
∴ △ ABD∽ △ A'B'D'
∴AD:A'D'=AB:A'B'=k
结论1 相似三角形对应高的比等于相似比。
试一试:
若AD、 A'D'分别为BC 、B'C'边上的中线,那么AD、 A'D'之间有什么关系?若AD、 A'D'分别为∠BAC 、 ∠ B'A'C'的角平分线呢?
结论2 相似三角形对应中线、
对应角平分线的比均为相似比。
A
B
C
D
B '
C '
A'
D '
定理1:相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比。
A
B
C
B '
C '
A'
如左图,已知:△ ABC ∽ △ A'B'C',且它们的相似比为k。求:它们的周长比。
解:
∵ △ ABC∽ △ A'B'C'
∴
∴
定理2: 相似三角形周长的比等于相似比。
继续探究
做一做
如下图⑴、⑵、⑶分别是边长为1、2、3的等边三角形,它们都相似。
⑴
⑵
⑶
⑵与⑴的相似比=( )
⑵与⑴的面积比=( )
⑶与⑴的相似比=( )
⑶与⑴的面积比=( )
由此我们可以得到什么结论?
对等边三角形而言,面积比=相似比的平方。
2:1
4:1
3:1
9:1
动动你聪明的
脑子,想一想
上述结论是否适用于一般的相似三角形?
A
B
C
A′
B′
C′
D
D′
证明:
∽ △
△
分别过A、A′,
作AD⊥BC于D,
∵
∴
∴
∴
定理3 相似三角形面积的比等于相似比的平方。
例1:如图,一块铁皮呈锐角三角形,它的边BC=80cm,高AD=60cm。要把它加工成矩形零件,使矩形的长、宽之比为2:1,并且矩形长的一边位于边BC上,另两个顶点分别在边AB、AC上。求这个矩形零件的长与宽。
A
B
C
┐
D
解:如图,矩形PQRS为加工成的矩形零件,边SR在BC上,顶点P、Q分别在AB、AC上, △ ABC的高AD交PQ于点E。设PS为xcm,则PQ为2xcm。
∵
PQ//BC
∴
△ APQ∽ △ ABC
∴
即
解方程,得
因而,这个矩形零件的长是48cm,宽是24cm.
P
Q
S
R
E
请回答
1、若两个三角形的相似比为3:5,则这两个三角形对应高的比为( ),对应角平分线的比为( ),周长之比为( ),对应中线之比为( )。
2、把一个三角形改成和它相似的三角形,如果面积扩大为原来的100倍,那么边长扩大为原来的几倍?
3、已知两个等边三角形的边长之比为2:3,且它们的面积之和为26cm2,则较小的等边三角形的面积为多少?
3:5
3:5
3:5
10倍
8cm2
3:5
小试牛刀:
小试牛刀
4、顺次连接三角形三边中点所得的三角形与原三
角形周长比是_____,面积比是
1/2
1/4
再接再厉
5,如图DE∥BC,EF∥AB,S△ADE=25,S△CEF=36.
求△ABC的面积.
A
B
C
D
E
F
25
36
解:∵DE∥BC,EF∥AB
∴∠A=∠CEF,∠AED=∠C
∴△ADE∽△EFC
∴
∵DE∥BC
∴△ADE∽△ABC
∵ S△ADE=25
∴S △ABC=121
∴
∴
∴
E
A
B
C
.
6、如图, 在△ABC中,AB=5,AC=4,E是AB上一点,AE=2, 在AC上取一点F,使以A、E、F为顶点的三角形与 △ABC相似,那么AF=________
F2
F1
再接再厉
D
Q
A
B
C
P
如图, 边长为4的正方形ABCD中, P是边BC上的一点, QP⊥AP
交 DC于Q, 设
BP= x, △ADQ的面积为y.
(1) 求y与x之间的函数关系式,并求自变量x的取值范围;
(2) 问P点在何位置时,△ADQ的面积最小 最小面积是多少
相似与函数的相关习题
对于例1,要使得内接矩形PQRS的面积最大,此时该矩形的长与宽各是多少?
拓展练习
P
Q
S
R
E
A
B
C
┐
D
1、相似三角形对应边成____,对应角______.
2、相似三角形对应边上的高、对应边上的中线、
对应角平分线的比都等于________.
3、相似三角形周长的比等于________,
相似三角形面积的比等于______________.
课堂小结
相似比的平方
相似三角形的性质
比例
相等
相似比
相似比
谢 谢
