2021--2022学年七年级数学下册 5.2.2平行线的判定 课件(共17张)
文档属性
| 名称 | 2021--2022学年七年级数学下册 5.2.2平行线的判定 课件(共17张) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-31 22:52:55 | ||
图片预览





文档简介
(共17张PPT)
5.2.2平行线的判定(一)
目录
一、情景导入.
二、两直线平行的判定
三、课堂练习
四、课堂小结
PART.01
一、情景导入.
装修工人正在向墙上钉木条,如果木条b与墙壁边缘垂直,那么木条a与墙壁边缘所夹角为多少度时,才能使木条a与木条b平行?要解决这个问题,就要弄清楚平行的判定。
a
b
二、两直线平行的判定
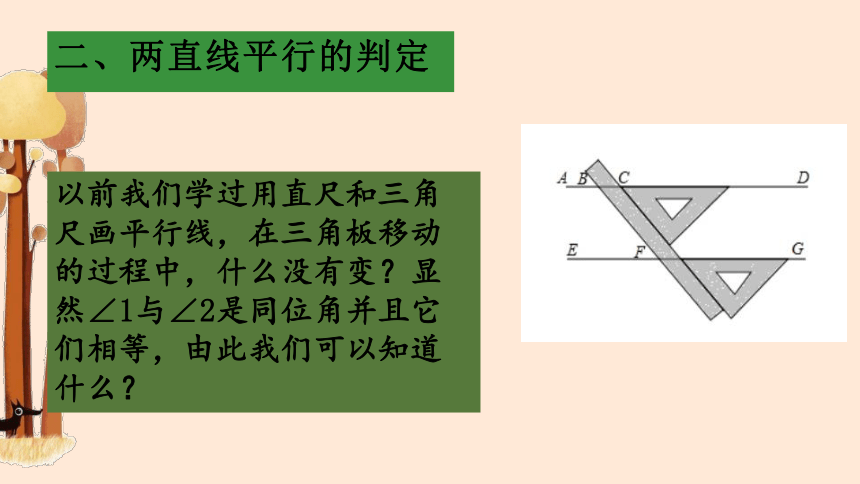
以前我们学过用直尺和三角尺画平行线,在三角板移动的过程中,什么没有变?显然∠1与∠2是同位角并且它们相等,由此我们可以知道什么?
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
判定一:
2
b
a
c
1
简单地说:同位角相等,两直线平行.
符号语言:
∵∠1=∠2
∴a∥b(同位角相等,两直线平行)
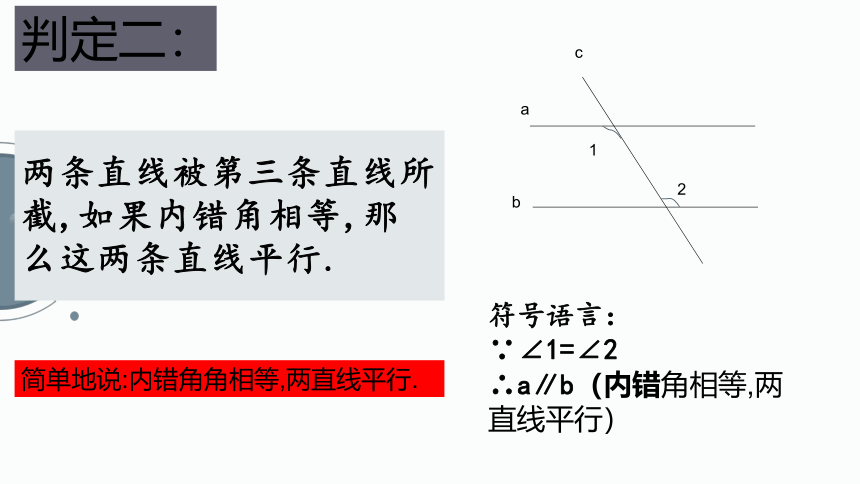
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
判定二:
2
b
a
c
1
简单地说:内错角角相等,两直线平行.
符号语言:
∵∠1=∠2
∴a∥b(内错角相等,两直线平行)
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
判定三:
2
b
a
c
1
简单地说:同旁内角互补,两直线平行.
符号语言:
∵∠1+∠2=180°
∴a∥b(同旁内角互补,两直线平行)
三,课堂练习:
1.如图,在下列所给条件中,不能判断AB∥DF的是:( )
A.∠1=∠4
B.∠1=∠2
C.∠2+∠A=180°
D.∠3=∠A
B
2.如图,已知∠1=∠2,则下列结论一定成立的是( )
A.AB//CD
B.AD//BC
C.∠B=∠D
D.∠3=∠4
答案:B.
解析 :∵∠1=∠2,
∴AD//BC.
故选B. 考点:平行线的判定
3. 下列图形中,能由∠1=∠2得到AB//CD的是( )
A. B. C. D.
答案: D.
解析 :根据同位角相等两直线平行可得答案 : 由∠1=∠2得到AB∥CD的是D选项, ∵∠1=∠2,∠3=∠2, ∴∠1=∠3, ∴AB∥CD. 故选 D.
4. 对于图中标记的各角,下列条件能推理得到a∥b的是( )
A.∠1=∠2 B.∠2=∠4
C.∠3=∠4 D.∠1+∠4=180
答案: D.
解析 ; A、∠1=∠2,因为它们不是a、b被截得的同位角或内错角,不符合题意;
B、∠2=∠4,因为它们不是a、b被截得的同位角或内错角,不符合题意;
C、∠3=∠4,因为它们不是a、b被截得的同位角或内错角,不符合题意;
D、∠1+∠4=180°,∠1的对顶角与∠4是a、b被截得的同旁内角,符合题意. 故选 D.
5. 如图,已知∠1=70°,要使AB∥CD,则须具备另一个条件( )
A.∠2=70° B.∠2=100°
C.∠2=110° D.∠3=110°
答案: C.
解析 :∠1=70°,要使AB∥CD, 则只要∠2=180°-70°=110°(同旁内角互补两直线平行). 故选 C. 考点:平行线的判定.
四、课堂小结
5.2.1平行线的判定
1、同位角相等,两直线平行.2、内错角相等,两直线平行.3、同旁内角互补,两直线平行.
拔高训练:
7. 如图,已知:∠B=∠D+∠E,试说明:AB∥CD.
答案:说明见解析.
解析 :根据三角形的外角的性质可得∠BFD=∠D+∠E,
则∠B=∠BFD,根据内错角相等,两直线平行,即可证得.
试题解析:
∵∠BFD=∠D+∠E,
又∵∠B=∠D+∠E,
∴∠B=∠BFD,
∴AB∥CD.
考点:平行线的判定
谢谢聆听
5.2.2平行线的判定(一)
目录
一、情景导入.
二、两直线平行的判定
三、课堂练习
四、课堂小结
PART.01
一、情景导入.
装修工人正在向墙上钉木条,如果木条b与墙壁边缘垂直,那么木条a与墙壁边缘所夹角为多少度时,才能使木条a与木条b平行?要解决这个问题,就要弄清楚平行的判定。
a
b
二、两直线平行的判定
以前我们学过用直尺和三角尺画平行线,在三角板移动的过程中,什么没有变?显然∠1与∠2是同位角并且它们相等,由此我们可以知道什么?
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
判定一:
2
b
a
c
1
简单地说:同位角相等,两直线平行.
符号语言:
∵∠1=∠2
∴a∥b(同位角相等,两直线平行)
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
判定二:
2
b
a
c
1
简单地说:内错角角相等,两直线平行.
符号语言:
∵∠1=∠2
∴a∥b(内错角相等,两直线平行)
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
判定三:
2
b
a
c
1
简单地说:同旁内角互补,两直线平行.
符号语言:
∵∠1+∠2=180°
∴a∥b(同旁内角互补,两直线平行)
三,课堂练习:
1.如图,在下列所给条件中,不能判断AB∥DF的是:( )
A.∠1=∠4
B.∠1=∠2
C.∠2+∠A=180°
D.∠3=∠A
B
2.如图,已知∠1=∠2,则下列结论一定成立的是( )
A.AB//CD
B.AD//BC
C.∠B=∠D
D.∠3=∠4
答案:B.
解析 :∵∠1=∠2,
∴AD//BC.
故选B. 考点:平行线的判定
3. 下列图形中,能由∠1=∠2得到AB//CD的是( )
A. B. C. D.
答案: D.
解析 :根据同位角相等两直线平行可得答案 : 由∠1=∠2得到AB∥CD的是D选项, ∵∠1=∠2,∠3=∠2, ∴∠1=∠3, ∴AB∥CD. 故选 D.
4. 对于图中标记的各角,下列条件能推理得到a∥b的是( )
A.∠1=∠2 B.∠2=∠4
C.∠3=∠4 D.∠1+∠4=180
答案: D.
解析 ; A、∠1=∠2,因为它们不是a、b被截得的同位角或内错角,不符合题意;
B、∠2=∠4,因为它们不是a、b被截得的同位角或内错角,不符合题意;
C、∠3=∠4,因为它们不是a、b被截得的同位角或内错角,不符合题意;
D、∠1+∠4=180°,∠1的对顶角与∠4是a、b被截得的同旁内角,符合题意. 故选 D.
5. 如图,已知∠1=70°,要使AB∥CD,则须具备另一个条件( )
A.∠2=70° B.∠2=100°
C.∠2=110° D.∠3=110°
答案: C.
解析 :∠1=70°,要使AB∥CD, 则只要∠2=180°-70°=110°(同旁内角互补两直线平行). 故选 C. 考点:平行线的判定.
四、课堂小结
5.2.1平行线的判定
1、同位角相等,两直线平行.2、内错角相等,两直线平行.3、同旁内角互补,两直线平行.
拔高训练:
7. 如图,已知:∠B=∠D+∠E,试说明:AB∥CD.
答案:说明见解析.
解析 :根据三角形的外角的性质可得∠BFD=∠D+∠E,
则∠B=∠BFD,根据内错角相等,两直线平行,即可证得.
试题解析:
∵∠BFD=∠D+∠E,
又∵∠B=∠D+∠E,
∴∠B=∠BFD,
∴AB∥CD.
考点:平行线的判定
谢谢聆听
