青岛版初中数学七年级上册 第3章有理数的运算复习课件(共19张PPT)
文档属性
| 名称 | 青岛版初中数学七年级上册 第3章有理数的运算复习课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 383.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-01 10:44:33 | ||
图片预览






文档简介
(共19张PPT)
第3章 有理数的运算
复习课件
学习目标
1.进一步掌握有理数的运算法则和运算律。
2.使学生能够熟练地按有理数运算顺序进行混合运 算,注意培养学生的运算能力。
3.掌握科学记数法,会按要求取一个数的近似数。
学习重点、难点
重点:有理数的加法和乘法法则及运算律。
难点:有理数异号两数相加法则及两个负数相乘的法则。加减混合运算写成省略加号和的形式,并能应用运算律简化运算。
有
理
数
的
运
算
除法
运算
加法
减法
乘法
乘方
混合运算
乘法结合律
加法交换律
加法结合律
乘法分配律
乘法交换律
简便运算
运算律
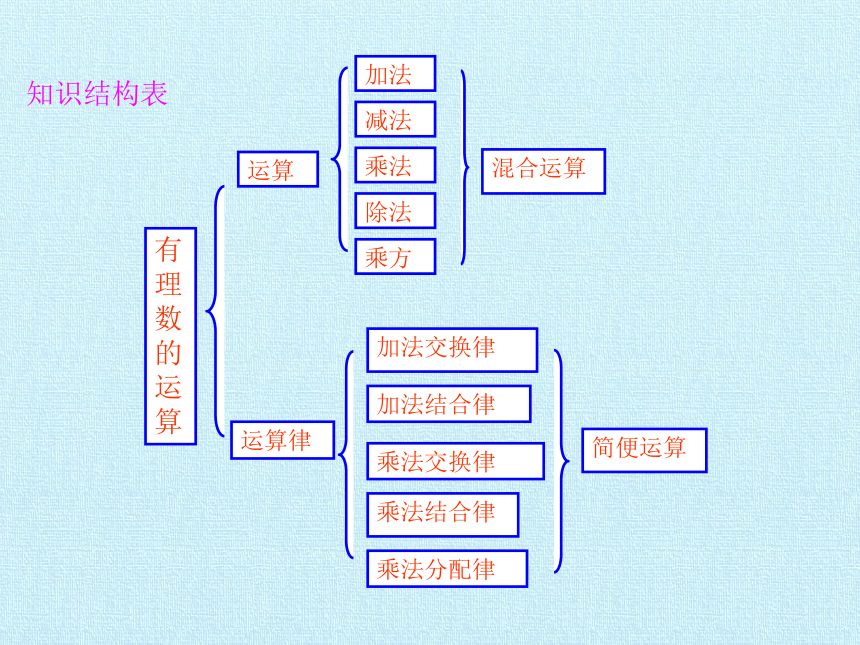
知识结构表
课前复习 1、有理数的加法、减法、乘法、除法及乘方法则
2、加法、乘法运算律
3、科学记数法,会按要求取一个数的近似数。
1.加法
(1)法则:
同号两数相加,取相同的符号,并把绝对值相加;绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值;一个数与0相加,仍得这个数;互为相反数的两个数相加得0。
(2)运算律:
a+b=b+a (a+b)+c=a+(b+c)
一.复习巩固
2.减法法则
减去一个数,等于加上
这个数的相反数。
3.乘法
(1)法则:两数相乘,同号得正,异号得负,并把绝对值相乘;任何数与零相乘积仍得零。
(2)运算律 axb=bxa (axb)xc=ax(bxc)
(a+b)xc=axc+bxc
(3)几个不等于0的数相乘,积的符号由负因数的个数决定。当负因数为奇数个时,积为负;当负因数为偶数个时,积为正。几个有理数相乘,如果其中有一个因数为0,积就为0.
4.除法法则
(1)两数相除,同号得正,异号得负并把绝对值相除;
(2)0除以任何一个不等于0的数,都得0。
0不能做除数。
(3)除以一个不为0的数,等于乘这个数的倒数。
5.有理数的乘方
6.科学记数法
正数的任何次幂都是正数;负数的偶次幂是正数,
负数的奇次幂是负数;0的任何正整数次幂都等于0。
把一个绝对值大于10的数记作ax10n形式,其中a是整数位数只有一位的数,n是正整数,比原数的整数位数少1。
7.有理数混合运算的法则
先算乘方,再算乘除,最后算加减;同级运算,按从左到右的顺序进行;如果有括号,先算括号里面的,并按小括号、中括号、大括号的顺序进行。
典型例题
解:原式
解:原式
典型例题
1.计算:
(1)-43×22-(-4)3×(-2)2 ;
(2)- 5×32 -(-5×3)2 ;
(3)(- —)÷(— - — - —);
12
4
8
8
7
7
7
7
-3
-270
0
达标反馈
达标反馈
2.填空
(1)-70900 000用科学记数法表示为__________。用科学记数法表示的数5.96x104 ,原数是__________。
(2)由四舍五入得到的近似数7.061x107,精确到
_________位。
-7.09x107
59600
万
牛刀小试
(1)1.5-2×(-3)
(2)
(3)
(4)
-18
-3
0
-7
1.计算
2.计算
2
-22
28
原式=74 -4 ÷2= 74 -2= 72
原式=9/4 -8= -23/4
原式=8-2×1/3=8-2/3=22/3
原式=-9-(-8)=-9+8=-1
(1)74-4÷2=70÷2=35
(1)74-4÷2=70÷2=35
3.下列计算错在哪里?应该如何改正?
(2)
(3)
(4)
这节课,我的收获是---
回顾小结,
突出重点
谢 谢
第3章 有理数的运算
复习课件
学习目标
1.进一步掌握有理数的运算法则和运算律。
2.使学生能够熟练地按有理数运算顺序进行混合运 算,注意培养学生的运算能力。
3.掌握科学记数法,会按要求取一个数的近似数。
学习重点、难点
重点:有理数的加法和乘法法则及运算律。
难点:有理数异号两数相加法则及两个负数相乘的法则。加减混合运算写成省略加号和的形式,并能应用运算律简化运算。
有
理
数
的
运
算
除法
运算
加法
减法
乘法
乘方
混合运算
乘法结合律
加法交换律
加法结合律
乘法分配律
乘法交换律
简便运算
运算律
知识结构表
课前复习 1、有理数的加法、减法、乘法、除法及乘方法则
2、加法、乘法运算律
3、科学记数法,会按要求取一个数的近似数。
1.加法
(1)法则:
同号两数相加,取相同的符号,并把绝对值相加;绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值;一个数与0相加,仍得这个数;互为相反数的两个数相加得0。
(2)运算律:
a+b=b+a (a+b)+c=a+(b+c)
一.复习巩固
2.减法法则
减去一个数,等于加上
这个数的相反数。
3.乘法
(1)法则:两数相乘,同号得正,异号得负,并把绝对值相乘;任何数与零相乘积仍得零。
(2)运算律 axb=bxa (axb)xc=ax(bxc)
(a+b)xc=axc+bxc
(3)几个不等于0的数相乘,积的符号由负因数的个数决定。当负因数为奇数个时,积为负;当负因数为偶数个时,积为正。几个有理数相乘,如果其中有一个因数为0,积就为0.
4.除法法则
(1)两数相除,同号得正,异号得负并把绝对值相除;
(2)0除以任何一个不等于0的数,都得0。
0不能做除数。
(3)除以一个不为0的数,等于乘这个数的倒数。
5.有理数的乘方
6.科学记数法
正数的任何次幂都是正数;负数的偶次幂是正数,
负数的奇次幂是负数;0的任何正整数次幂都等于0。
把一个绝对值大于10的数记作ax10n形式,其中a是整数位数只有一位的数,n是正整数,比原数的整数位数少1。
7.有理数混合运算的法则
先算乘方,再算乘除,最后算加减;同级运算,按从左到右的顺序进行;如果有括号,先算括号里面的,并按小括号、中括号、大括号的顺序进行。
典型例题
解:原式
解:原式
典型例题
1.计算:
(1)-43×22-(-4)3×(-2)2 ;
(2)- 5×32 -(-5×3)2 ;
(3)(- —)÷(— - — - —);
12
4
8
8
7
7
7
7
-3
-270
0
达标反馈
达标反馈
2.填空
(1)-70900 000用科学记数法表示为__________。用科学记数法表示的数5.96x104 ,原数是__________。
(2)由四舍五入得到的近似数7.061x107,精确到
_________位。
-7.09x107
59600
万
牛刀小试
(1)1.5-2×(-3)
(2)
(3)
(4)
-18
-3
0
-7
1.计算
2.计算
2
-22
28
原式=74 -4 ÷2= 74 -2= 72
原式=9/4 -8= -23/4
原式=8-2×1/3=8-2/3=22/3
原式=-9-(-8)=-9+8=-1
(1)74-4÷2=70÷2=35
(1)74-4÷2=70÷2=35
3.下列计算错在哪里?应该如何改正?
(2)
(3)
(4)
这节课,我的收获是---
回顾小结,
突出重点
谢 谢
同课章节目录
- 第1章 基本的几何图形
- 1.1 我们身边的图形世界
- 1.2 几何图形
- 1.3 线段、射线和直线
- 1.4 线段的比较与作法
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数与绝对值
- 第3章 有理数的运算
- 3.1 有理数的加法与减法
- 3.2 有理数的乘法与除法
- 3.3 有理数的乘方
- 3.4 有理数的混合运算
- 3.5 利用计算器进行有理数的计算
- 第4章 数据的收集整理与描述
- 4.1 普查和抽样调查
- 4.2 简单随机抽样
- 4.3 数据的整理
- 4.4 扇形统计图
- 第5章 代数式与函数的初步认识
- 5.1 用字母表示数
- 5.2 代数式
- 5.3 代数式的值
- 5.4 生活中的常量与变量
- 5.5 函数的初步认识
- 第6章 整式的加减
- 6.1 单项式与多项式
- 6.2 同类项
- 6.3 去括号
- 6.4 整式的加减
- 第7章 一元一次方程
- 7.1 等式的基本性质
- 7.2 一元一次方程
- 7.3 一元一次方程的解法
- 7.4 一元一次方程的应用
