沪科版数学九年级上册 23.2 解直角三角形(教案)
文档属性
| 名称 | 沪科版数学九年级上册 23.2 解直角三角形(教案) |

|
|
| 格式 | docx | ||
| 文件大小 | 97.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-01 00:00:00 | ||
图片预览

文档简介
课题:23.2解直角三角形教学设计
课 题 23.2 解直角三角形
年 级 九年级(上) 教材版本 沪科版
教 学 目 标 理解直角三角形中五个元素的关系,会运用勾股定理,直角三角形的两个锐角互余及锐角三角函数解直角三角形,并能解决简单的应用. 2、逐步培养学生分析问题、解决问题的能力. 3、渗透数形结合、转化等数学思想方法,培养学生良好的学习习惯.
学 情 分 析 学生在次之前已经学习了直角三角形的一些知识,如:勾股定理、正弦、余弦、正切等。在此基础上学习综合运用勾股定理、锐角三角函数的知识解直角三角形,为运用直角三角形的知识解决实际问题打下良好的基础,进而展示数学的应用价值,增强学生应用数学知识的意识。
重点难点 重点:解直角三角形。 难点:灵活运用锐角三角函数解直角三角形。
【教学过程】
教学环节 教师活动 学生活动 设计意图
知识回顾 教师活动:在图形的研究中,直角三角形是常见的三角形之一,因而人们经常会遇到求直角三角形的边长或角度等问题。对于这类问题,我们一般利用锐角三角函数的有关知识来解决。这节课我们学习解直角三角形。 (板书:解直角三角形) (课件展示) (1)在直角三角形中,除直角外共有几个元素? (2)如图,在Rt△ABC 中∠C=90°,a、b、c、∠A、∠B这五个元素间有哪些等量关系呢? 引导学生复习回顾. 回忆并说出除直角外的5个元素。 独立思考并回答直角三角形的三边,两锐角,边与角之间的关系。 师生共识:解直角三角形的定义。 通过结构式的知识回顾让学生感受数学知识是环环相扣的,能让学生为接下来的学习作很好的铺垫和自然的过渡。带着他们的疑问来学习解直角三角形,去探索解直角三角形的条件,激发了他们研究的兴趣和探究的激情。
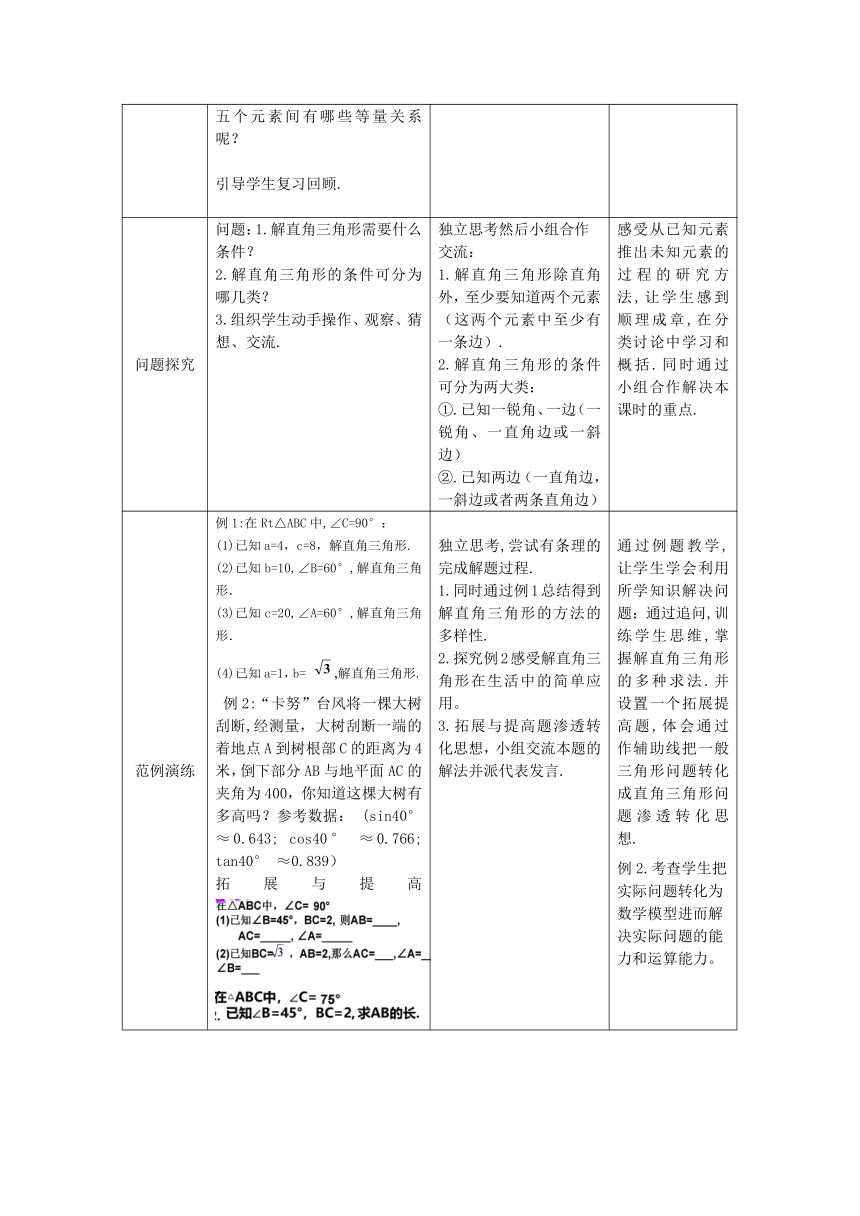
问题探究 问题:1.解直角三角形需要什么条件? 2.解直角三角形的条件可分为哪几类? 3.组织学生动手操作、观察、猜想、交流. 独立思考然后小组合作交流: 1.解直角三角形除直角外,至少要知道两个元素(这两个元素中至少有一条边). 2.解直角三角形的条件可分为两大类: ①.已知一锐角、一边(一锐角、一直角边或一斜边) ②.已知两边(一直角边,一斜边或者两条直角边) 感受从已知元素推出未知元素的过程的研究方法,让学生感到顺理成章,在分类讨论中学习和概括.同时通过小组合作解决本课时的重点.
范例演练 例1:在Rt△ABC中,∠C=90°: (1)已知a=4,c=8,解直角三角形. (2)已知b=10,∠B=60°,解直角三角形. (3)已知c=20,∠A=60°,解直角三角形. (4)已知a=1,b= ,解直角三角形. 例2:“卡努”台风将一棵大树刮断,经测量,大树刮断一端的着地点A到树根部C的距离为4米,倒下部分AB与地平面AC的夹角为400,你知道这棵大树有多高吗?参考数据: (sin40°≈0.643; cos40° ≈0.766; tan40° ≈0.839) 拓展与提高 独立思考,尝试有条理的完成解题过程. 1.同时通过例1总结得到解直角三角形的方法的多样性. 2.探究例2感受解直角三角形在生活中的简单应用。 3.拓展与提高题渗透转化思想,小组交流本题的解法并派代表发言. 通过例题教学,让学生学会利用所学知识解决问题;通过追问,训练学生思维,掌握解直角三角形的多种求法.并设置一个拓展提高题,体会通过作辅助线把一般三角形问题转化成直角三角形问题渗透转化思想. 例2.考查学生把实际问题转化为数学模型进而解决实际问题的能力和运算能力。
合作探究 拿出你事先准备的特殊直角三角形,拼一拼,你能给出其中的一些元素,求出某些元素的值吗?请试一试,然后派代表发言。 展示近几年安徽中考真题初步感受解直角三角形的考查方式。 发散思维: 如图,在四边形ABCD中, AB=2,CD=1, ∠A= 60°, ∠D= ∠B= 90°,求此四边形ABCD的面积。 通过小组合作初步感受双直角三角形模型,并尝试给出相关元素求另外一个元素。 初步感受中考真题对于解直角三角形的常见考查方式和题目类型以及本质。 通过一题多解体会构造直角三角形的多样性。 使学生巩固利用直角三角形的有关知识解决实际问题,考察建立数学模型的能力,转化的数学思想在学习中的应用,提高学生分析问题、解决问题的能力。 培养学生构建知识,形成知识体系,同时让学生体会化归思想. 同时通过一题多解渗透解法的多样性发散学生的思维。
自我总结 引导学生总结并得出知识框架图: 通过这节课的学习 在知识上你收获了...... 在思想方法上...... 系统梳理、归纳本节课自己的收获并且有条理的表达出来: 在知识上... 在思想方法上... 我的疑惑... 对于他人的发言认真倾听和质疑反思. 培养学生的反思能力,追寻数学思想,总结数学方法,启迪学生的思维,培养学生总结反思的能力.框架图式总结,更容易形成知识网络.
当堂检测 发放当堂检测卷 反馈测试情况,对于错误多的集中讲授。个别错误单独辅导。 1.学生独立完成并交卷. 2.个别错误找同伴或老师解决。同时吸取他人错误的经验教训。 (
第3题
) (
第3题
) 当堂检测,及时反馈,考查学生目标的达成度,进而改进教学,实现教学相长.
布置作业 必做题:P125第1.2题 全品两面。 选做题:一艘船向东航行,上午8时到达B处,看到有一灯塔在它的北偏东60°,距离为72海里的A处;上午10时到达C处,看到灯塔在它的正北方向.求这艘船航行的速度。(用根号表示) 独立完成作业, 学困生组内帮扶. 关注学生的个体差异,设置必做题和选做题,使每一个学生都有成功的体验,得到相应的提高与发展,体现课标的“使不同的学生得到不同的发展”这一宗旨.
课 题 23.2 解直角三角形
年 级 九年级(上) 教材版本 沪科版
教 学 目 标 理解直角三角形中五个元素的关系,会运用勾股定理,直角三角形的两个锐角互余及锐角三角函数解直角三角形,并能解决简单的应用. 2、逐步培养学生分析问题、解决问题的能力. 3、渗透数形结合、转化等数学思想方法,培养学生良好的学习习惯.
学 情 分 析 学生在次之前已经学习了直角三角形的一些知识,如:勾股定理、正弦、余弦、正切等。在此基础上学习综合运用勾股定理、锐角三角函数的知识解直角三角形,为运用直角三角形的知识解决实际问题打下良好的基础,进而展示数学的应用价值,增强学生应用数学知识的意识。
重点难点 重点:解直角三角形。 难点:灵活运用锐角三角函数解直角三角形。
【教学过程】
教学环节 教师活动 学生活动 设计意图
知识回顾 教师活动:在图形的研究中,直角三角形是常见的三角形之一,因而人们经常会遇到求直角三角形的边长或角度等问题。对于这类问题,我们一般利用锐角三角函数的有关知识来解决。这节课我们学习解直角三角形。 (板书:解直角三角形) (课件展示) (1)在直角三角形中,除直角外共有几个元素? (2)如图,在Rt△ABC 中∠C=90°,a、b、c、∠A、∠B这五个元素间有哪些等量关系呢? 引导学生复习回顾. 回忆并说出除直角外的5个元素。 独立思考并回答直角三角形的三边,两锐角,边与角之间的关系。 师生共识:解直角三角形的定义。 通过结构式的知识回顾让学生感受数学知识是环环相扣的,能让学生为接下来的学习作很好的铺垫和自然的过渡。带着他们的疑问来学习解直角三角形,去探索解直角三角形的条件,激发了他们研究的兴趣和探究的激情。
问题探究 问题:1.解直角三角形需要什么条件? 2.解直角三角形的条件可分为哪几类? 3.组织学生动手操作、观察、猜想、交流. 独立思考然后小组合作交流: 1.解直角三角形除直角外,至少要知道两个元素(这两个元素中至少有一条边). 2.解直角三角形的条件可分为两大类: ①.已知一锐角、一边(一锐角、一直角边或一斜边) ②.已知两边(一直角边,一斜边或者两条直角边) 感受从已知元素推出未知元素的过程的研究方法,让学生感到顺理成章,在分类讨论中学习和概括.同时通过小组合作解决本课时的重点.
范例演练 例1:在Rt△ABC中,∠C=90°: (1)已知a=4,c=8,解直角三角形. (2)已知b=10,∠B=60°,解直角三角形. (3)已知c=20,∠A=60°,解直角三角形. (4)已知a=1,b= ,解直角三角形. 例2:“卡努”台风将一棵大树刮断,经测量,大树刮断一端的着地点A到树根部C的距离为4米,倒下部分AB与地平面AC的夹角为400,你知道这棵大树有多高吗?参考数据: (sin40°≈0.643; cos40° ≈0.766; tan40° ≈0.839) 拓展与提高 独立思考,尝试有条理的完成解题过程. 1.同时通过例1总结得到解直角三角形的方法的多样性. 2.探究例2感受解直角三角形在生活中的简单应用。 3.拓展与提高题渗透转化思想,小组交流本题的解法并派代表发言. 通过例题教学,让学生学会利用所学知识解决问题;通过追问,训练学生思维,掌握解直角三角形的多种求法.并设置一个拓展提高题,体会通过作辅助线把一般三角形问题转化成直角三角形问题渗透转化思想. 例2.考查学生把实际问题转化为数学模型进而解决实际问题的能力和运算能力。
合作探究 拿出你事先准备的特殊直角三角形,拼一拼,你能给出其中的一些元素,求出某些元素的值吗?请试一试,然后派代表发言。 展示近几年安徽中考真题初步感受解直角三角形的考查方式。 发散思维: 如图,在四边形ABCD中, AB=2,CD=1, ∠A= 60°, ∠D= ∠B= 90°,求此四边形ABCD的面积。 通过小组合作初步感受双直角三角形模型,并尝试给出相关元素求另外一个元素。 初步感受中考真题对于解直角三角形的常见考查方式和题目类型以及本质。 通过一题多解体会构造直角三角形的多样性。 使学生巩固利用直角三角形的有关知识解决实际问题,考察建立数学模型的能力,转化的数学思想在学习中的应用,提高学生分析问题、解决问题的能力。 培养学生构建知识,形成知识体系,同时让学生体会化归思想. 同时通过一题多解渗透解法的多样性发散学生的思维。
自我总结 引导学生总结并得出知识框架图: 通过这节课的学习 在知识上你收获了...... 在思想方法上...... 系统梳理、归纳本节课自己的收获并且有条理的表达出来: 在知识上... 在思想方法上... 我的疑惑... 对于他人的发言认真倾听和质疑反思. 培养学生的反思能力,追寻数学思想,总结数学方法,启迪学生的思维,培养学生总结反思的能力.框架图式总结,更容易形成知识网络.
当堂检测 发放当堂检测卷 反馈测试情况,对于错误多的集中讲授。个别错误单独辅导。 1.学生独立完成并交卷. 2.个别错误找同伴或老师解决。同时吸取他人错误的经验教训。 (
第3题
) (
第3题
) 当堂检测,及时反馈,考查学生目标的达成度,进而改进教学,实现教学相长.
布置作业 必做题:P125第1.2题 全品两面。 选做题:一艘船向东航行,上午8时到达B处,看到有一灯塔在它的北偏东60°,距离为72海里的A处;上午10时到达C处,看到灯塔在它的正北方向.求这艘船航行的速度。(用根号表示) 独立完成作业, 学困生组内帮扶. 关注学生的个体差异,设置必做题和选做题,使每一个学生都有成功的体验,得到相应的提高与发展,体现课标的“使不同的学生得到不同的发展”这一宗旨.
