人教版七年级数学下册 5.2.1 平行线 教案(表格式)
文档属性
| 名称 | 人教版七年级数学下册 5.2.1 平行线 教案(表格式) |  | |
| 格式 | docx | ||
| 文件大小 | 173.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-01 17:01:43 | ||
图片预览



文档简介
5.2.1 平行线
课题 5.2.1 平行线 授课人
教 学 目 标 知识技能 1.理解平行线的意义,了解同一平面内两条直线的位置关系; 2.理解并掌握平行公理及其推论的内容; 3.会根据几何语句画图,会用直尺和三角尺画平行线.
数学思考 能从模型的操作及实际生活中抽象出平行线的概念
问题解决 能过直线外一点画出已知直线的平行线.
情感态度 通过对几何模型的操作,培养学生的直觉思维和创造性思维,使学生获得成就感.
教学 重点 探索和掌握平行公理及其推论.
教学 难点 对平行公理的理解.
授课 类型 新授课 课时
教具 三线相交模型
教学活动
教学 步骤 师生活动 设计意图
活动 一: 创设 情境 导入 新课 【课堂引入】 (多媒体展示) 如图5-2-5,观察生活中的图片. 图5-2-5 思考:图中的游泳池中的分道线、铁轨、操场上跑道中的分道线会不会出现交点 在位置上给人怎样的感觉 通过生活中常见的情景引入新课,激发学生的学习兴趣.
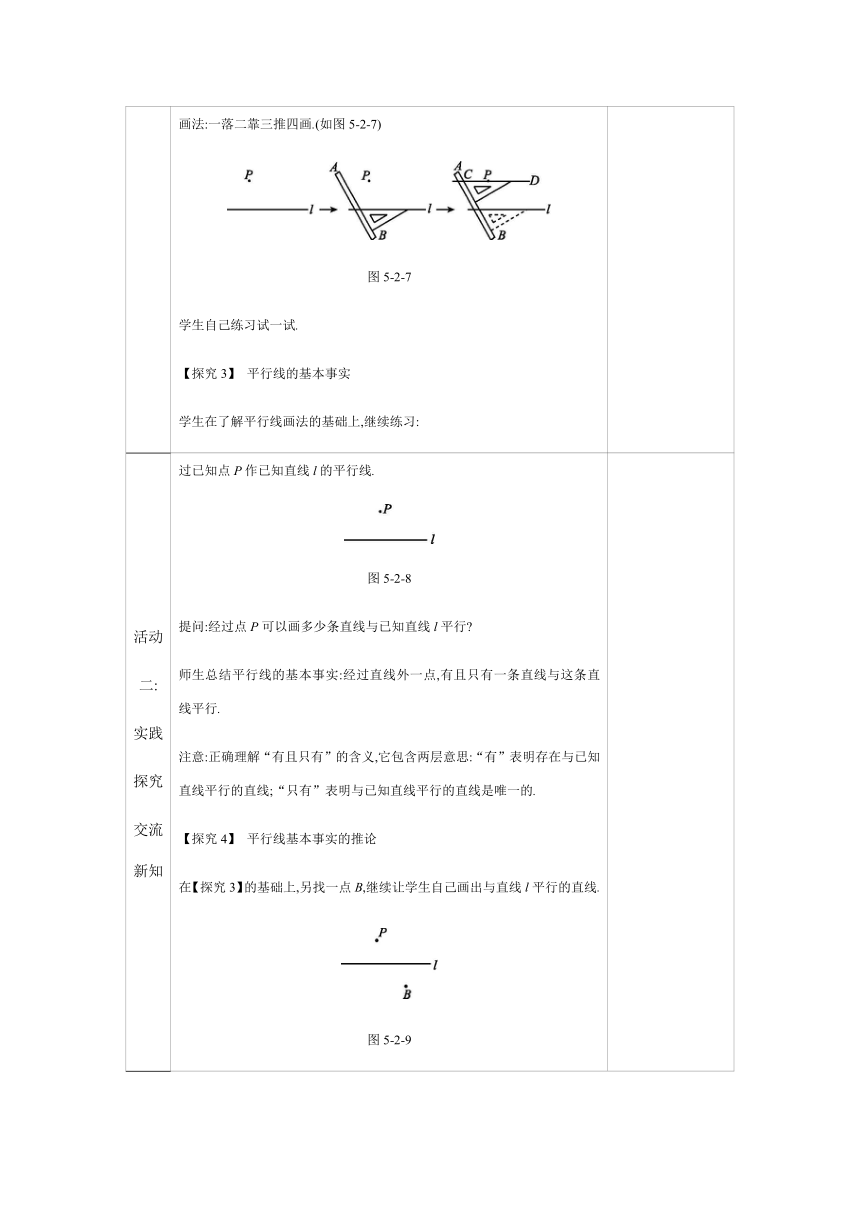
活动 二: 实践 探究 交流 新知 【探究1】 探究平行线的特点 平行线的特点:(1)在同一平面且不相交;(2)直线. 定义:在同一平面内不相交的两条直线叫平行线. 表示方法:如图5-2-6所示的两条直线a,b互相平行,记作“a∥b”,读作a平行于b. 图5-2-6 问题: (1)平行线应该满足哪些条件 [同一平面内、不相交(即无交点)] (2)同一平面内不重合的两条直线有哪些位置关系 (平行与相交) 【探究2】 平行线的画法 先由学生思考,然后教师归纳并示范平行线的画法. 画法:一落二靠三推四画.(如图5-2-7) 图5-2-7 学生自己练习试一试. 【探究3】 平行线的基本事实 学生在了解平行线画法的基础上,继续练习: 1.通过对平行线画法的讲解,培养学生分析问题、动手动脑的能力,在独立练习中体会手脑结合的乐趣. 2.以画平行线为线索,循序渐进,一步一步让学生自己归纳出平行线的基本事实及其推论.
活动 二: 实践 探究 交流 新知 过已知点P作已知直线l的平行线. 图5-2-8 提问:经过点P可以画多少条直线与已知直线l平行 师生总结平行线的基本事实:经过直线外一点,有且只有一条直线与这条直线平行. 注意:正确理解“有且只有”的含义,它包含两层意思:“有”表明存在与已知直线平行的直线;“只有”表明与已知直线平行的直线是唯一的. 【探究4】 平行线基本事实的推论 在【探究3】的基础上,另找一点B,继续让学生自己画出与直线l平行的直线. 图5-2-9 提问:在这三条直线中,任意两条直线的关系是什么样的 师生共同得出一个结论: 如果两条直线都与第三条直线平行,那么这两条直线也互相平行.
活动 三: 开放 训练 体现 应用 【应用举例】 例1 如图5-2-10,已知直线a和点B,C. (1)过点B画直线a的平行线,能画几条 (2)过点C画直线a的平行线,它与(1)中所作的直线平行吗 图5-2-10 图5-2-11 解:(1)如图5-2-11,过直线a外的一点B画直线a的平行线,有且只有一条直线与直线a平行. (2)如图5-2-11,过点C画直线a的平行线,它与(1)中所作的直线平行.理由如下: 因为b∥a,c∥a, 所以c∥b. 利用新知解决问题,根据相关性质进行推理.
活动 三: 开放 训练 体现 应用 【拓展提升】 例2 在同一平面内三条直线会有怎样的位置关系和交点个数 解:(1)如图5-2-12①,三条直线互相平行,此时交点个数为0; (2)如图②,三条直线相交于一点,此时交点个数为1; (3)如图③,三条直线两两相交且不交于一点,此时交点的个数是3; (4)如图④,其中两条直线平行,都与第三条直线相交,此时交点个数是2. 图5-2-12 知识的综合与拓展,提高应考能力,培养学生大胆尝试、勇于探索的精神,提高学生的思维能力.
活动 四: 课堂 总结 反思 【当堂训练】 一、填空题 1.在同一平面内,两条不重合的直线的位置关系有 相交和平行 两种. 2.两条直线相交,交点的个数是 1 ,两条直线平行,交点的个数是 0 . 二、判断题 1.如果一条直线与两条平行线其中的一条平行,那么它与另一条直线也互相平行. (√) 2.过一点有且只有一条直线平行于已知直线. (×) 课后作业: 课本第15页习题5.2第3,8,9,11题. 通过练习进一步巩固所学平行线的概念及性质
【知识网络】 框架图式总结,更容易形成知识网络.
【教学反思】 ①[授课流程反思] 本节从学生熟悉的、常见的身边事物出发引入平行线的概念,亲切自然、能充分调动学生学习的积极性. ②[讲授效果反思] 通过本节教学,学生理解了平面中两直线的位置关系,基本掌握平行公理及其推论,为后继学习打下基础.
活动 四: 课堂 总结 反思 ③[师生互动反思] 学生是学习的主体,教师在学生学习过程中起引导作用.本节课教师引导学生发现身边的平行现象,然后让学生归纳两直线平行的概念.归纳平行公理的推论时对学生的学习过程进行了进一步的深入指导. ④[习题反思] 好题题号 错题题号 回顾反思,找出差距与不足,形成知识及数学体系,更进一步提升教师教学能力.
一、自学范围(12页练习)
二、自学目标:
1、了解平行线的概念、平面内两条直线相交和平行的两种位置关系, 知道平行公理以及平行公理的推论.
2.会用符号语言表示平行公理推论, 会用三角尺和直尺过已知直线外一点画这条直线的平行线.
三、自学重点:
平行公理也及平行公理的推论
四、自学过程:
1、自学12页思考,体会在平面内两条直线能存在几种位置关系?
2、根据课本填空:在同一平面内,如果存在一条直线a与直线b不相交的位置,这时直线a与直线b互相 ,记作:
3、举出生活中平行的例子。
4、在同一平面内,不重合的两条直线有几种位置关系?动手画一画。
5、自学13页上方的思考:(该怎样经过一点画已知直线的平行线呢)(提示:参考一下13页下面的思考)
用三角尺和直尺分别过B点和C点作直线a的平行线b和c。
(1)过点B能作 条 (2)过点C能作 条
6、平行公理:经过直线外一点,有且只有 条直线与这条直线平行。
7、在上面的作图中,b∥a c∥a,那b与c平行吗?
推论:如果两条直线都与第三直线平行,那么这两条直线也互相平行。(想一想为什么)
五、学效测试:
8、12页练习
9、在同一平面内,两条不重合直线的位置关系可能是( )毛
A.平行或相交 B.垂直或相交;C.垂直或平行 D.平行、垂直或相交
10、下列说法正确的是( )
A.经过一点有一条直线与已知直线平行
B.经过一点有无数条直线与已知直线平行
C.经过一点有且只有一条直线与已知直线平行
D.经过直线外一点有且只有一条直线与已知直线平行
11、在同一平面内有三条直线,若其中有两条且只有两条直线平行,则它们交点的个数为( )
A.0个 B.1个 C.2个 D.3个
12.下列说法正确的有( )
①不相交的两条直线是平行线;②在同一平面内,两条直线的位置关系有两种;
③若线段AB与CD没有交点,则AB∥CD;④若a∥b,b∥c,则a与c不相交.
A.1个 B.2个 C.3个 D.4个
课题 5.2.1 平行线 授课人
教 学 目 标 知识技能 1.理解平行线的意义,了解同一平面内两条直线的位置关系; 2.理解并掌握平行公理及其推论的内容; 3.会根据几何语句画图,会用直尺和三角尺画平行线.
数学思考 能从模型的操作及实际生活中抽象出平行线的概念
问题解决 能过直线外一点画出已知直线的平行线.
情感态度 通过对几何模型的操作,培养学生的直觉思维和创造性思维,使学生获得成就感.
教学 重点 探索和掌握平行公理及其推论.
教学 难点 对平行公理的理解.
授课 类型 新授课 课时
教具 三线相交模型
教学活动
教学 步骤 师生活动 设计意图
活动 一: 创设 情境 导入 新课 【课堂引入】 (多媒体展示) 如图5-2-5,观察生活中的图片. 图5-2-5 思考:图中的游泳池中的分道线、铁轨、操场上跑道中的分道线会不会出现交点 在位置上给人怎样的感觉 通过生活中常见的情景引入新课,激发学生的学习兴趣.
活动 二: 实践 探究 交流 新知 【探究1】 探究平行线的特点 平行线的特点:(1)在同一平面且不相交;(2)直线. 定义:在同一平面内不相交的两条直线叫平行线. 表示方法:如图5-2-6所示的两条直线a,b互相平行,记作“a∥b”,读作a平行于b. 图5-2-6 问题: (1)平行线应该满足哪些条件 [同一平面内、不相交(即无交点)] (2)同一平面内不重合的两条直线有哪些位置关系 (平行与相交) 【探究2】 平行线的画法 先由学生思考,然后教师归纳并示范平行线的画法. 画法:一落二靠三推四画.(如图5-2-7) 图5-2-7 学生自己练习试一试. 【探究3】 平行线的基本事实 学生在了解平行线画法的基础上,继续练习: 1.通过对平行线画法的讲解,培养学生分析问题、动手动脑的能力,在独立练习中体会手脑结合的乐趣. 2.以画平行线为线索,循序渐进,一步一步让学生自己归纳出平行线的基本事实及其推论.
活动 二: 实践 探究 交流 新知 过已知点P作已知直线l的平行线. 图5-2-8 提问:经过点P可以画多少条直线与已知直线l平行 师生总结平行线的基本事实:经过直线外一点,有且只有一条直线与这条直线平行. 注意:正确理解“有且只有”的含义,它包含两层意思:“有”表明存在与已知直线平行的直线;“只有”表明与已知直线平行的直线是唯一的. 【探究4】 平行线基本事实的推论 在【探究3】的基础上,另找一点B,继续让学生自己画出与直线l平行的直线. 图5-2-9 提问:在这三条直线中,任意两条直线的关系是什么样的 师生共同得出一个结论: 如果两条直线都与第三条直线平行,那么这两条直线也互相平行.
活动 三: 开放 训练 体现 应用 【应用举例】 例1 如图5-2-10,已知直线a和点B,C. (1)过点B画直线a的平行线,能画几条 (2)过点C画直线a的平行线,它与(1)中所作的直线平行吗 图5-2-10 图5-2-11 解:(1)如图5-2-11,过直线a外的一点B画直线a的平行线,有且只有一条直线与直线a平行. (2)如图5-2-11,过点C画直线a的平行线,它与(1)中所作的直线平行.理由如下: 因为b∥a,c∥a, 所以c∥b. 利用新知解决问题,根据相关性质进行推理.
活动 三: 开放 训练 体现 应用 【拓展提升】 例2 在同一平面内三条直线会有怎样的位置关系和交点个数 解:(1)如图5-2-12①,三条直线互相平行,此时交点个数为0; (2)如图②,三条直线相交于一点,此时交点个数为1; (3)如图③,三条直线两两相交且不交于一点,此时交点的个数是3; (4)如图④,其中两条直线平行,都与第三条直线相交,此时交点个数是2. 图5-2-12 知识的综合与拓展,提高应考能力,培养学生大胆尝试、勇于探索的精神,提高学生的思维能力.
活动 四: 课堂 总结 反思 【当堂训练】 一、填空题 1.在同一平面内,两条不重合的直线的位置关系有 相交和平行 两种. 2.两条直线相交,交点的个数是 1 ,两条直线平行,交点的个数是 0 . 二、判断题 1.如果一条直线与两条平行线其中的一条平行,那么它与另一条直线也互相平行. (√) 2.过一点有且只有一条直线平行于已知直线. (×) 课后作业: 课本第15页习题5.2第3,8,9,11题. 通过练习进一步巩固所学平行线的概念及性质
【知识网络】 框架图式总结,更容易形成知识网络.
【教学反思】 ①[授课流程反思] 本节从学生熟悉的、常见的身边事物出发引入平行线的概念,亲切自然、能充分调动学生学习的积极性. ②[讲授效果反思] 通过本节教学,学生理解了平面中两直线的位置关系,基本掌握平行公理及其推论,为后继学习打下基础.
活动 四: 课堂 总结 反思 ③[师生互动反思] 学生是学习的主体,教师在学生学习过程中起引导作用.本节课教师引导学生发现身边的平行现象,然后让学生归纳两直线平行的概念.归纳平行公理的推论时对学生的学习过程进行了进一步的深入指导. ④[习题反思] 好题题号 错题题号 回顾反思,找出差距与不足,形成知识及数学体系,更进一步提升教师教学能力.
一、自学范围(12页练习)
二、自学目标:
1、了解平行线的概念、平面内两条直线相交和平行的两种位置关系, 知道平行公理以及平行公理的推论.
2.会用符号语言表示平行公理推论, 会用三角尺和直尺过已知直线外一点画这条直线的平行线.
三、自学重点:
平行公理也及平行公理的推论
四、自学过程:
1、自学12页思考,体会在平面内两条直线能存在几种位置关系?
2、根据课本填空:在同一平面内,如果存在一条直线a与直线b不相交的位置,这时直线a与直线b互相 ,记作:
3、举出生活中平行的例子。
4、在同一平面内,不重合的两条直线有几种位置关系?动手画一画。
5、自学13页上方的思考:(该怎样经过一点画已知直线的平行线呢)(提示:参考一下13页下面的思考)
用三角尺和直尺分别过B点和C点作直线a的平行线b和c。
(1)过点B能作 条 (2)过点C能作 条
6、平行公理:经过直线外一点,有且只有 条直线与这条直线平行。
7、在上面的作图中,b∥a c∥a,那b与c平行吗?
推论:如果两条直线都与第三直线平行,那么这两条直线也互相平行。(想一想为什么)
五、学效测试:
8、12页练习
9、在同一平面内,两条不重合直线的位置关系可能是( )毛
A.平行或相交 B.垂直或相交;C.垂直或平行 D.平行、垂直或相交
10、下列说法正确的是( )
A.经过一点有一条直线与已知直线平行
B.经过一点有无数条直线与已知直线平行
C.经过一点有且只有一条直线与已知直线平行
D.经过直线外一点有且只有一条直线与已知直线平行
11、在同一平面内有三条直线,若其中有两条且只有两条直线平行,则它们交点的个数为( )
A.0个 B.1个 C.2个 D.3个
12.下列说法正确的有( )
①不相交的两条直线是平行线;②在同一平面内,两条直线的位置关系有两种;
③若线段AB与CD没有交点,则AB∥CD;④若a∥b,b∥c,则a与c不相交.
A.1个 B.2个 C.3个 D.4个
