2021-2022学年北师大版八年级数学上册1.3勾股定理的应用 期末综合复习训练 (Word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版八年级数学上册1.3勾股定理的应用 期末综合复习训练 (Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 297.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-30 22:33:02 | ||
图片预览



文档简介
2021-2022学年北师大版八年级数学上册《勾股定理的应用》期末综合复习训练(附答案)
1.如图,一棵大树在离地面6米高的B处断裂,树顶A落在离树底部C的8米处,则大树断裂之前的高度为( )
A.10米 B.16米 C.15米 D.14米
2.在平静的湖面上,有一支红莲,高出水面1米,阵风吹来,红莲被吹到一边,花朵齐及水面,已知红莲移动的水平距离为2米,问这里水深是( )
A.1米 B.1.5米 C.2米 D.2.5米
3.如图所示:有一个长、宽都是2米,高为3米的长方体纸盒,一只小蚂蚁从A点爬到B点,那么这只蚂蚁爬行的最短路径为( )
A.3米 B.4米 C.5米 D.6米
4.如图是一个三级台阶,它的每一级的长,宽,高分别为100cm,15cm和10cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁想到B点去吃可口的食物,则它所走的最短路线长度为( )
A.115cm B.125cm C.135cm D.145cm
5.如图,一只蚂蚁从长宽都是3,高是8的长方体纸箱的A点沿纸箱爬到B点,那么它所行的最短路线的长是( )
A.3+8 B.10 C.14 D.无法确定
6.我国古代著名的“赵爽弦图”的示意图如图所示,它是由四个全等的直角三角形围成的.若AC=2,BC=3,将四个直角三角形中边长为3的直角边分别向外延长一倍,得到一个如图所示“数学风车”,则这个风车的外围周长是( )
A. B.8 C. D.
7.一根长18cm的牙刷置于底面半径为5cm、高为12cm的圆柱形水杯中,牙刷露在杯子外面的长度为hcm,则h的值不可能是( )
A.3cm B.πcm C.6cm D.8cm
8.如图,有两棵树,一棵高19米,另一棵高10米,两树相距12米.若一只小鸟从一棵树的树梢飞到另一棵树的树梢,则小鸟至少飞行( )
A.10米 B.15米 C.16米 D.20米
9.如图,牧童在A处放牛,牧童家在B处,A、B处距河岸DC的距离AC、BD的长分别为500m和700m,且C,D两点的距离为500m,天黑前牧童从A处将牛牵到河边饮水再回家,那么牧童最少要走的距离为( )
A.1000m B.1200m C.1300m D.1700m
10.如图,公园里有一块草坪,已知AB=3米,BC=4米,CD=12米,DA=13米,且AB⊥BC,这块草坪的面积是( )
A.24平方米 B.36平方米 C.48平方米 D.72平方米
11.如图为某楼梯,测得楼梯的长为5米,高3米,计划在楼梯表面铺地毯,地毯的长度至少需要 米.
12.小明想知道学校旗杆有多高,他发现旗杆上的绳子垂到地面还余1m,当他把绳子下端拉开5m后,发现下端刚好接触地面,则旗杆高度为 米.
13.如图,一只蚂蚁从点A沿圆柱表面爬到点B,圆柱高为8cm,底面半径为cm,那么最短的路线长是 .
14.如图,一圆柱体的底面周长为10cm,高BD为12cm,BC是直径,一只蚂蚁从点D出发沿着圆柱的表面爬行到点C的最短路程为 cm.
15.一个底面周长为10cm,高为12cm的圆柱,有一只小虫从底部点A处爬到上底B处,则小虫所爬的最短路径长是 cm.
16.如图,要从A点(圆柱底面一点)环绕圆柱形侧面,建梯子到A点正上方的B点,若圆柱底面周长为12m,高AB为5m,则所建梯子最短需 m.
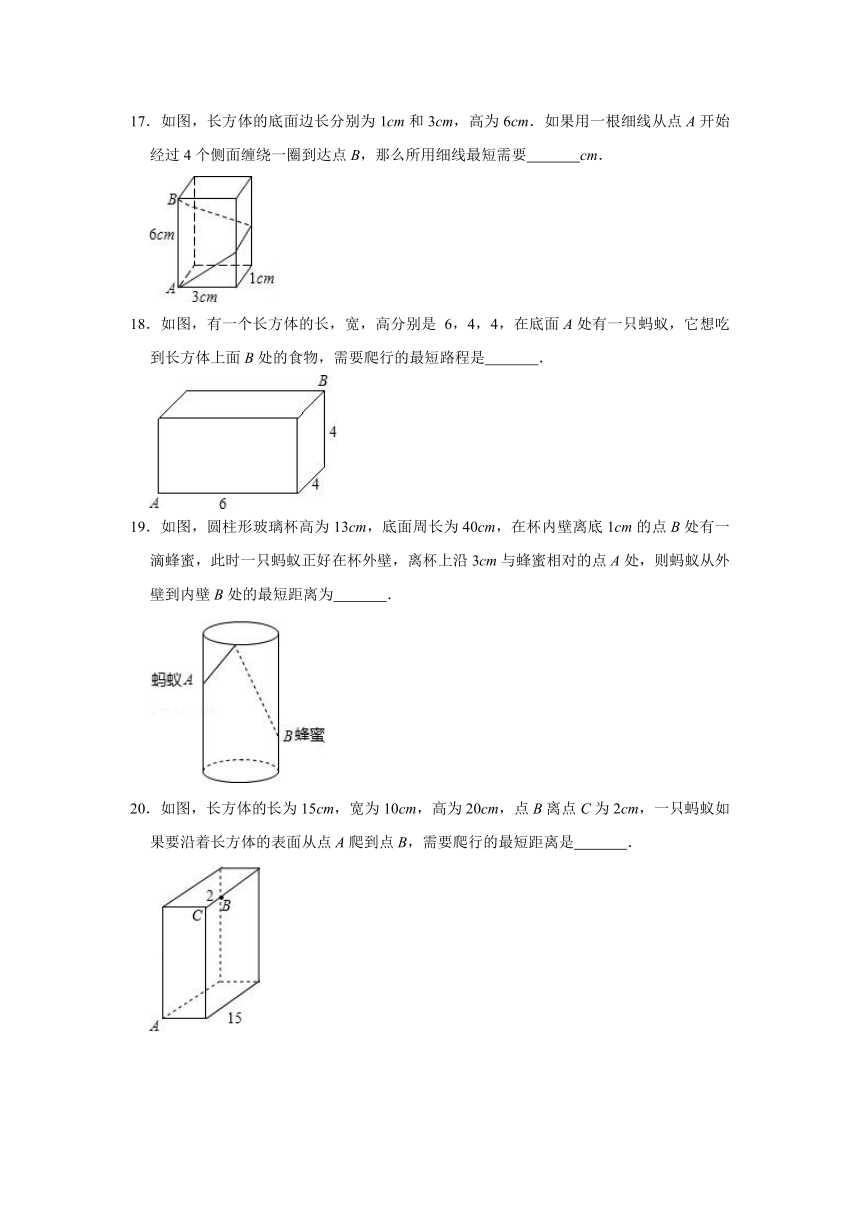
17.如图,长方体的底面边长分别为1cm和3cm,高为6cm.如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需要 cm.
18.如图,有一个长方体的长,宽,高分别是 6,4,4,在底面A处有一只蚂蚁,它想吃到长方体上面B处的食物,需要爬行的最短路程是 .
19.如图,圆柱形玻璃杯高为13cm,底面周长为40cm,在杯内壁离底1cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3cm与蜂蜜相对的点A处,则蚂蚁从外壁到内壁B处的最短距离为 .
20.如图,长方体的长为15cm,宽为10cm,高为20cm,点B离点C为2cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是 .
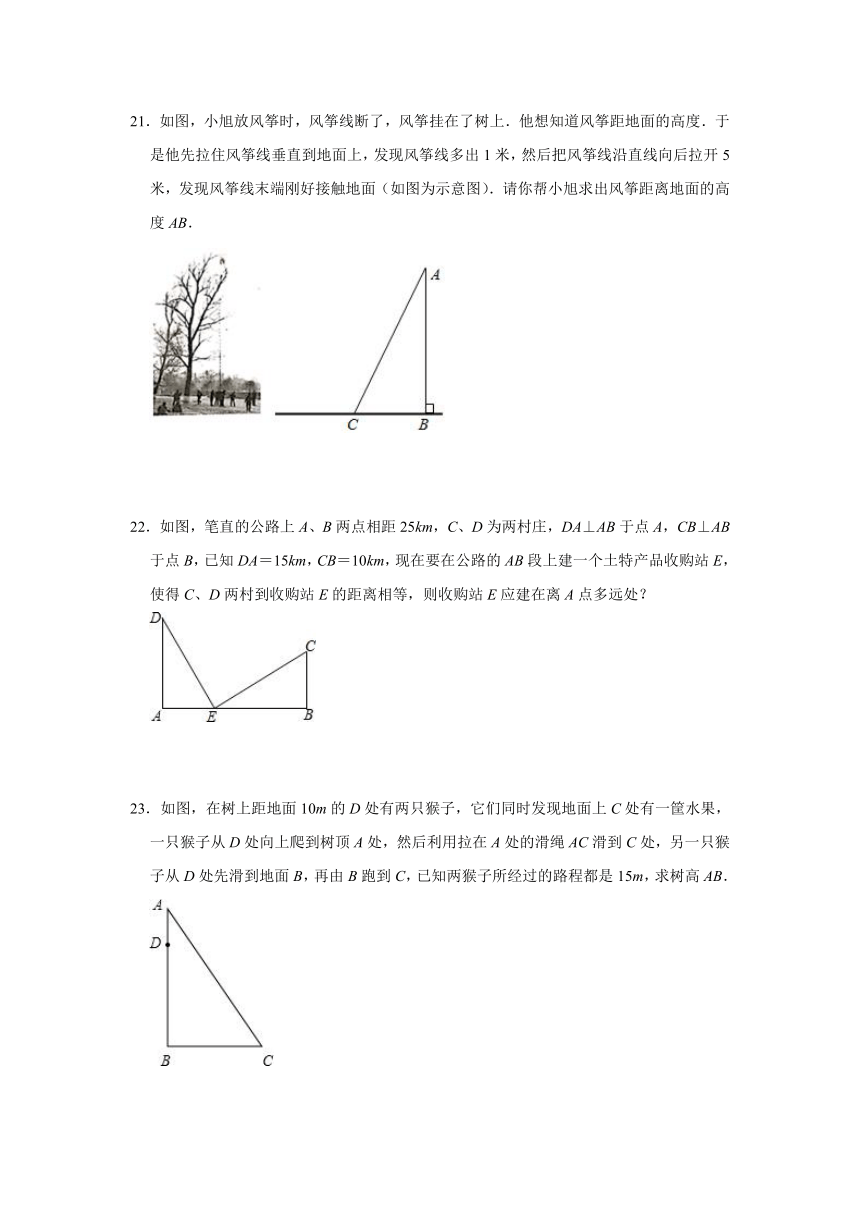
21.如图,小旭放风筝时,风筝线断了,风筝挂在了树上.他想知道风筝距地面的高度.于是他先拉住风筝线垂直到地面上,发现风筝线多出1米,然后把风筝线沿直线向后拉开5米,发现风筝线末端刚好接触地面(如图为示意图).请你帮小旭求出风筝距离地面的高度AB.
22.如图,笔直的公路上A、B两点相距25km,C、D为两村庄,DA⊥AB于点A,CB⊥AB于点B,已知DA=15km,CB=10km,现在要在公路的AB段上建一个土特产品收购站E,使得C、D两村到收购站E的距离相等,则收购站E应建在离A点多远处?
23.如图,在树上距地面10m的D处有两只猴子,它们同时发现地面上C处有一筐水果,一只猴子从D处向上爬到树顶A处,然后利用拉在A处的滑绳AC滑到C处,另一只猴子从D处先滑到地面B,再由B跑到C,已知两猴子所经过的路程都是15m,求树高AB.
24.如图所示的一块地,∠ADC=90°,AD=12m,CD=9m,AB=39m,BC=36m,求这块地的面积.
25.一架方梯长25米,如图,斜靠在一面墙上,梯子底端离墙7米,
(1)这个梯子的顶端距地面有多高?
(2)如果梯子的顶端下滑了4米,那么梯子的底端在水平方向滑动了几米?
参考答案
1.解:由题意得BC=6,在直角三角形ABC中,根据勾股定理得:AB===10米.
所以大树的高度是10+6=16米.
故选:B.
2.解:设水深为h,则红莲的高h+1,且水平距离为2m,
则(h+1)2=22+h2,解得h=1.5.
故选:B.
3.解:由题意得,
路径一:AB==;
路径二:AB==5;
路径三:AB==;
∵>5,
∴5为最短路径.
故选:C.
4.解:展开图为:
则AC=100cm,BC=15×3+10×3=75cm,
在Rt△ABC中,AB==125cm.
所以蚂蚁所走的最短路线长度为125cm.
故选:B.
5.解:将点A和点B所在的两个面展开,
则矩形的长和宽分别为6和8,
故矩形对角线长AB==10,
即蚂蚁所行的最短路线长是10.
故选:B.
6.解:依题意,设“数学风车”中的四个直角三角形的斜边长为x,
则x2=62+22=40,
所以x=2,
所以风车的外围周长为4(BD+AC)=4×(2+3)=8+12.
故选:D.
7.解:∵将一根长为18cm的牙刷,置于底面半径为5cm,高为12cm的圆柱形水杯中,
∴在杯子中牙刷最短是等于杯子的高,最长是等于杯子斜边长度,
∴当杯子中牙刷最短是等于杯子的高时,12cm,
最长时等于牙刷斜边长度是:=2cm,
∴h的取值范围是:(18﹣2)≤h≤(18﹣12),
即2<(18﹣2)≤h≤6.
故选:D.
8.解:如图,
建立数学模型,两棵树的高度差AC=19﹣10=9米,间距AB=DE=12米,
根据勾股定理可得:小鸟至少飞行的距离BC==15米.
故选:B.
9.解:作A点关于河岸的对称点A′,连接BA′交河岸与P,连接A′B′,连接PA,过A'作A'B'⊥BD于B',
则PB+PA=PB+PA′=BA′最短,故牧童应将马赶到河边的P地点.
∴B'D=A'C=CA=500m,
∴BB′=BD+BD′=700+500=1200(m),
∵A'B'=CD=500m,
∴BA'===1300(m).
即牧童至少要走的距离为1300m,
故选:C.
10.解:则由勾股定理得AC=5米,因为AC2+DC2=AD2,所以∠ACD=90°.
这块草坪的面积=SRt△ABC+SRt△ACD=AB BC+AC DC=(3×4+5×12)=36米2.
故选:B.
11.解:由勾股定理得:
楼梯的水平宽度==4,
∵地毯铺满楼梯时其长度的和应该是楼梯的水平宽度与垂直高度的和,
地毯的长度至少是3+4=7米.
故答案为7.
12.解:设旗杆高xm,则绳子长为(x+1)m,∵旗杆垂直于地面,
∴旗杆,绳子与地面构成直角三角形,由题意列式为x2+52=(x+1)2,解得x=12m.
13.解:连接AB,
∵圆柱的底面半径为cm,
∴AC=×2 π =6(cm),
在Rt△ACB中,AB2=AC2+CB2=36+64=100,
∴AB=10cm,即最短的路线长是10cm;
故答案为:10cm.
14.解:如图所示:
由于圆柱体的底面周长为10cm,
则AD=10×=5(cm).
又因为BD=AC=12cm,
所以DC===13(cm).
故蚂蚁从点D出发沿着圆柱的表面爬行到点C的最短路程为13cm.
故答案为:13.
15.解:展开圆柱的侧面如图,根据两点之间线段最短就可以得知AB最短.
由题意,得AC=10÷2=5,BC=12,
在Rt△ABC中,由勾股定理,得
AB==13cm.
故答案为:13.
16.解:把圆柱的侧面展开得到矩形ABCD,
则AC=12m,BC=5m,
由勾股定理得,AB==13m,
故答案为:13.
17.解:将长方体展开,连接A、B′,
∵AA′=1+3+1+3=8(cm),A′B′=6cm,
根据两点之间线段最短,AB′==10cm.
故答案为:10.
18.解:第一种情况:把我们所看到的前面和上面组成一个平面,
则这个长方形的长和宽分别是8和6,
则所走的最短线段是=10;
第二种情况:把我们看到的左面与上面组成一个长方形,
则这个长方形的长和宽分别是10和4,
所以走的最短线段是=2;
第三种情况:把我们所看到的前面和右面组成一个长方形,
则这个长方形的长和宽分别是10和4,
所以走的最短线段是 =2;
三种情况比较而言,第一种情况最短.
故答案为:10.
19.解:如图:
将杯子侧面展开,作A关于EF的对称点A′,
连接A′B,则A′B即为最短距离,A′B===25(cm).
故答案为25cm.
20.解:把右侧面展开到水平面上,连接AB,如图1,AB===2(cm);
把右侧面展开到正面上,连接AB,如图2,AB===4(cm);
把向上的面展开到正面上,连接AB,如图3,AB===2(cm).
所以一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离为4cm.
故答案为4cm.
21.解:设AB=x,则AC=x+1,
由图可得,∠ABC=90°,BC=5,
∴Rt△ABC中,AB2+BC2=AC2,
即x2+52=(x+1)2,
解得x=12,
答:风筝距离地面的高度AB为12米.
22.解:∵使得C,D两村到E站的距离相等.
∴DE=CE,
∵DA⊥AB于A,CB⊥AB于B,
∴∠A=∠B=90°,
∴AE2+AD2=DE2,BE2+BC2=EC2,
∴AE2+AD2=BE2+BC2,
设设AE=xkm,则BE=AB﹣AE=(25﹣x)km.
∵DA=15km,CB=10km,
∴x2+152=(25﹣x)2+102,
解得:x=10,
∴AE=10km,
∴收购站E应建在离A点10km处.
23.解:Rt△ABC中,∠B=90°,
设BC=a(m),AC=b(m),AD=x(m)
则10+a=x+b=15(m).
∴a=5(m),b=15﹣x(m)
又在Rt△ABC中,由勾股定理得:(10+x)2+a2=b2,
∴(10+x)2+52=(15﹣x)2,
解得,x=2,即AD=2(米)
∴AB=AD+DB=2+10=12(米)
答:树高AB为12米.
24.解:连接AC,
已知,在直角△ACD中,CD=9m,AD=12m,
根据AD2+CD2=AC2,可以求得AC=15m,
在△ABC中,AB=39m,BC=36m,AC=15m,
∴存在AC2+CB2=AB2,
∴△ABC为直角三角形,
要求这块地的面积,求△ABC和△ACD的面积之差即可,
S=S△ABC﹣S△ACD=AC BC﹣CD AD,
=×15×36﹣×9×12,
=270﹣54,
=216m2,
答:这块地的面积为216m2.
25.解:(1)根据勾股定理:
梯子距离地面的高度为:=24米;
(2)梯子下滑了4米,
即梯子距离地面的高度为A'B=AB﹣AA′=24﹣4=20,
根据勾股定理得:25=,
解得CC′=8.
即梯子的底端在水平方向滑动了8米.
1.如图,一棵大树在离地面6米高的B处断裂,树顶A落在离树底部C的8米处,则大树断裂之前的高度为( )
A.10米 B.16米 C.15米 D.14米
2.在平静的湖面上,有一支红莲,高出水面1米,阵风吹来,红莲被吹到一边,花朵齐及水面,已知红莲移动的水平距离为2米,问这里水深是( )
A.1米 B.1.5米 C.2米 D.2.5米
3.如图所示:有一个长、宽都是2米,高为3米的长方体纸盒,一只小蚂蚁从A点爬到B点,那么这只蚂蚁爬行的最短路径为( )
A.3米 B.4米 C.5米 D.6米
4.如图是一个三级台阶,它的每一级的长,宽,高分别为100cm,15cm和10cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁想到B点去吃可口的食物,则它所走的最短路线长度为( )
A.115cm B.125cm C.135cm D.145cm
5.如图,一只蚂蚁从长宽都是3,高是8的长方体纸箱的A点沿纸箱爬到B点,那么它所行的最短路线的长是( )
A.3+8 B.10 C.14 D.无法确定
6.我国古代著名的“赵爽弦图”的示意图如图所示,它是由四个全等的直角三角形围成的.若AC=2,BC=3,将四个直角三角形中边长为3的直角边分别向外延长一倍,得到一个如图所示“数学风车”,则这个风车的外围周长是( )
A. B.8 C. D.
7.一根长18cm的牙刷置于底面半径为5cm、高为12cm的圆柱形水杯中,牙刷露在杯子外面的长度为hcm,则h的值不可能是( )
A.3cm B.πcm C.6cm D.8cm
8.如图,有两棵树,一棵高19米,另一棵高10米,两树相距12米.若一只小鸟从一棵树的树梢飞到另一棵树的树梢,则小鸟至少飞行( )
A.10米 B.15米 C.16米 D.20米
9.如图,牧童在A处放牛,牧童家在B处,A、B处距河岸DC的距离AC、BD的长分别为500m和700m,且C,D两点的距离为500m,天黑前牧童从A处将牛牵到河边饮水再回家,那么牧童最少要走的距离为( )
A.1000m B.1200m C.1300m D.1700m
10.如图,公园里有一块草坪,已知AB=3米,BC=4米,CD=12米,DA=13米,且AB⊥BC,这块草坪的面积是( )
A.24平方米 B.36平方米 C.48平方米 D.72平方米
11.如图为某楼梯,测得楼梯的长为5米,高3米,计划在楼梯表面铺地毯,地毯的长度至少需要 米.
12.小明想知道学校旗杆有多高,他发现旗杆上的绳子垂到地面还余1m,当他把绳子下端拉开5m后,发现下端刚好接触地面,则旗杆高度为 米.
13.如图,一只蚂蚁从点A沿圆柱表面爬到点B,圆柱高为8cm,底面半径为cm,那么最短的路线长是 .
14.如图,一圆柱体的底面周长为10cm,高BD为12cm,BC是直径,一只蚂蚁从点D出发沿着圆柱的表面爬行到点C的最短路程为 cm.
15.一个底面周长为10cm,高为12cm的圆柱,有一只小虫从底部点A处爬到上底B处,则小虫所爬的最短路径长是 cm.
16.如图,要从A点(圆柱底面一点)环绕圆柱形侧面,建梯子到A点正上方的B点,若圆柱底面周长为12m,高AB为5m,则所建梯子最短需 m.
17.如图,长方体的底面边长分别为1cm和3cm,高为6cm.如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需要 cm.
18.如图,有一个长方体的长,宽,高分别是 6,4,4,在底面A处有一只蚂蚁,它想吃到长方体上面B处的食物,需要爬行的最短路程是 .
19.如图,圆柱形玻璃杯高为13cm,底面周长为40cm,在杯内壁离底1cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3cm与蜂蜜相对的点A处,则蚂蚁从外壁到内壁B处的最短距离为 .
20.如图,长方体的长为15cm,宽为10cm,高为20cm,点B离点C为2cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是 .
21.如图,小旭放风筝时,风筝线断了,风筝挂在了树上.他想知道风筝距地面的高度.于是他先拉住风筝线垂直到地面上,发现风筝线多出1米,然后把风筝线沿直线向后拉开5米,发现风筝线末端刚好接触地面(如图为示意图).请你帮小旭求出风筝距离地面的高度AB.
22.如图,笔直的公路上A、B两点相距25km,C、D为两村庄,DA⊥AB于点A,CB⊥AB于点B,已知DA=15km,CB=10km,现在要在公路的AB段上建一个土特产品收购站E,使得C、D两村到收购站E的距离相等,则收购站E应建在离A点多远处?
23.如图,在树上距地面10m的D处有两只猴子,它们同时发现地面上C处有一筐水果,一只猴子从D处向上爬到树顶A处,然后利用拉在A处的滑绳AC滑到C处,另一只猴子从D处先滑到地面B,再由B跑到C,已知两猴子所经过的路程都是15m,求树高AB.
24.如图所示的一块地,∠ADC=90°,AD=12m,CD=9m,AB=39m,BC=36m,求这块地的面积.
25.一架方梯长25米,如图,斜靠在一面墙上,梯子底端离墙7米,
(1)这个梯子的顶端距地面有多高?
(2)如果梯子的顶端下滑了4米,那么梯子的底端在水平方向滑动了几米?
参考答案
1.解:由题意得BC=6,在直角三角形ABC中,根据勾股定理得:AB===10米.
所以大树的高度是10+6=16米.
故选:B.
2.解:设水深为h,则红莲的高h+1,且水平距离为2m,
则(h+1)2=22+h2,解得h=1.5.
故选:B.
3.解:由题意得,
路径一:AB==;
路径二:AB==5;
路径三:AB==;
∵>5,
∴5为最短路径.
故选:C.
4.解:展开图为:
则AC=100cm,BC=15×3+10×3=75cm,
在Rt△ABC中,AB==125cm.
所以蚂蚁所走的最短路线长度为125cm.
故选:B.
5.解:将点A和点B所在的两个面展开,
则矩形的长和宽分别为6和8,
故矩形对角线长AB==10,
即蚂蚁所行的最短路线长是10.
故选:B.
6.解:依题意,设“数学风车”中的四个直角三角形的斜边长为x,
则x2=62+22=40,
所以x=2,
所以风车的外围周长为4(BD+AC)=4×(2+3)=8+12.
故选:D.
7.解:∵将一根长为18cm的牙刷,置于底面半径为5cm,高为12cm的圆柱形水杯中,
∴在杯子中牙刷最短是等于杯子的高,最长是等于杯子斜边长度,
∴当杯子中牙刷最短是等于杯子的高时,12cm,
最长时等于牙刷斜边长度是:=2cm,
∴h的取值范围是:(18﹣2)≤h≤(18﹣12),
即2<(18﹣2)≤h≤6.
故选:D.
8.解:如图,
建立数学模型,两棵树的高度差AC=19﹣10=9米,间距AB=DE=12米,
根据勾股定理可得:小鸟至少飞行的距离BC==15米.
故选:B.
9.解:作A点关于河岸的对称点A′,连接BA′交河岸与P,连接A′B′,连接PA,过A'作A'B'⊥BD于B',
则PB+PA=PB+PA′=BA′最短,故牧童应将马赶到河边的P地点.
∴B'D=A'C=CA=500m,
∴BB′=BD+BD′=700+500=1200(m),
∵A'B'=CD=500m,
∴BA'===1300(m).
即牧童至少要走的距离为1300m,
故选:C.
10.解:则由勾股定理得AC=5米,因为AC2+DC2=AD2,所以∠ACD=90°.
这块草坪的面积=SRt△ABC+SRt△ACD=AB BC+AC DC=(3×4+5×12)=36米2.
故选:B.
11.解:由勾股定理得:
楼梯的水平宽度==4,
∵地毯铺满楼梯时其长度的和应该是楼梯的水平宽度与垂直高度的和,
地毯的长度至少是3+4=7米.
故答案为7.
12.解:设旗杆高xm,则绳子长为(x+1)m,∵旗杆垂直于地面,
∴旗杆,绳子与地面构成直角三角形,由题意列式为x2+52=(x+1)2,解得x=12m.
13.解:连接AB,
∵圆柱的底面半径为cm,
∴AC=×2 π =6(cm),
在Rt△ACB中,AB2=AC2+CB2=36+64=100,
∴AB=10cm,即最短的路线长是10cm;
故答案为:10cm.
14.解:如图所示:
由于圆柱体的底面周长为10cm,
则AD=10×=5(cm).
又因为BD=AC=12cm,
所以DC===13(cm).
故蚂蚁从点D出发沿着圆柱的表面爬行到点C的最短路程为13cm.
故答案为:13.
15.解:展开圆柱的侧面如图,根据两点之间线段最短就可以得知AB最短.
由题意,得AC=10÷2=5,BC=12,
在Rt△ABC中,由勾股定理,得
AB==13cm.
故答案为:13.
16.解:把圆柱的侧面展开得到矩形ABCD,
则AC=12m,BC=5m,
由勾股定理得,AB==13m,
故答案为:13.
17.解:将长方体展开,连接A、B′,
∵AA′=1+3+1+3=8(cm),A′B′=6cm,
根据两点之间线段最短,AB′==10cm.
故答案为:10.
18.解:第一种情况:把我们所看到的前面和上面组成一个平面,
则这个长方形的长和宽分别是8和6,
则所走的最短线段是=10;
第二种情况:把我们看到的左面与上面组成一个长方形,
则这个长方形的长和宽分别是10和4,
所以走的最短线段是=2;
第三种情况:把我们所看到的前面和右面组成一个长方形,
则这个长方形的长和宽分别是10和4,
所以走的最短线段是 =2;
三种情况比较而言,第一种情况最短.
故答案为:10.
19.解:如图:
将杯子侧面展开,作A关于EF的对称点A′,
连接A′B,则A′B即为最短距离,A′B===25(cm).
故答案为25cm.
20.解:把右侧面展开到水平面上,连接AB,如图1,AB===2(cm);
把右侧面展开到正面上,连接AB,如图2,AB===4(cm);
把向上的面展开到正面上,连接AB,如图3,AB===2(cm).
所以一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离为4cm.
故答案为4cm.
21.解:设AB=x,则AC=x+1,
由图可得,∠ABC=90°,BC=5,
∴Rt△ABC中,AB2+BC2=AC2,
即x2+52=(x+1)2,
解得x=12,
答:风筝距离地面的高度AB为12米.
22.解:∵使得C,D两村到E站的距离相等.
∴DE=CE,
∵DA⊥AB于A,CB⊥AB于B,
∴∠A=∠B=90°,
∴AE2+AD2=DE2,BE2+BC2=EC2,
∴AE2+AD2=BE2+BC2,
设设AE=xkm,则BE=AB﹣AE=(25﹣x)km.
∵DA=15km,CB=10km,
∴x2+152=(25﹣x)2+102,
解得:x=10,
∴AE=10km,
∴收购站E应建在离A点10km处.
23.解:Rt△ABC中,∠B=90°,
设BC=a(m),AC=b(m),AD=x(m)
则10+a=x+b=15(m).
∴a=5(m),b=15﹣x(m)
又在Rt△ABC中,由勾股定理得:(10+x)2+a2=b2,
∴(10+x)2+52=(15﹣x)2,
解得,x=2,即AD=2(米)
∴AB=AD+DB=2+10=12(米)
答:树高AB为12米.
24.解:连接AC,
已知,在直角△ACD中,CD=9m,AD=12m,
根据AD2+CD2=AC2,可以求得AC=15m,
在△ABC中,AB=39m,BC=36m,AC=15m,
∴存在AC2+CB2=AB2,
∴△ABC为直角三角形,
要求这块地的面积,求△ABC和△ACD的面积之差即可,
S=S△ABC﹣S△ACD=AC BC﹣CD AD,
=×15×36﹣×9×12,
=270﹣54,
=216m2,
答:这块地的面积为216m2.
25.解:(1)根据勾股定理:
梯子距离地面的高度为:=24米;
(2)梯子下滑了4米,
即梯子距离地面的高度为A'B=AB﹣AA′=24﹣4=20,
根据勾股定理得:25=,
解得CC′=8.
即梯子的底端在水平方向滑动了8米.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
