2021-2022学年北师大版八年级数学上册4.4一次函数的应用 期末综合复习训练 (Word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版八年级数学上册4.4一次函数的应用 期末综合复习训练 (Word版含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 676.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-30 00:00:00 | ||
图片预览

文档简介
2021-2022学年北师大版八年级数学上册《一次函数的应用》期末综合复习训练(附答案)
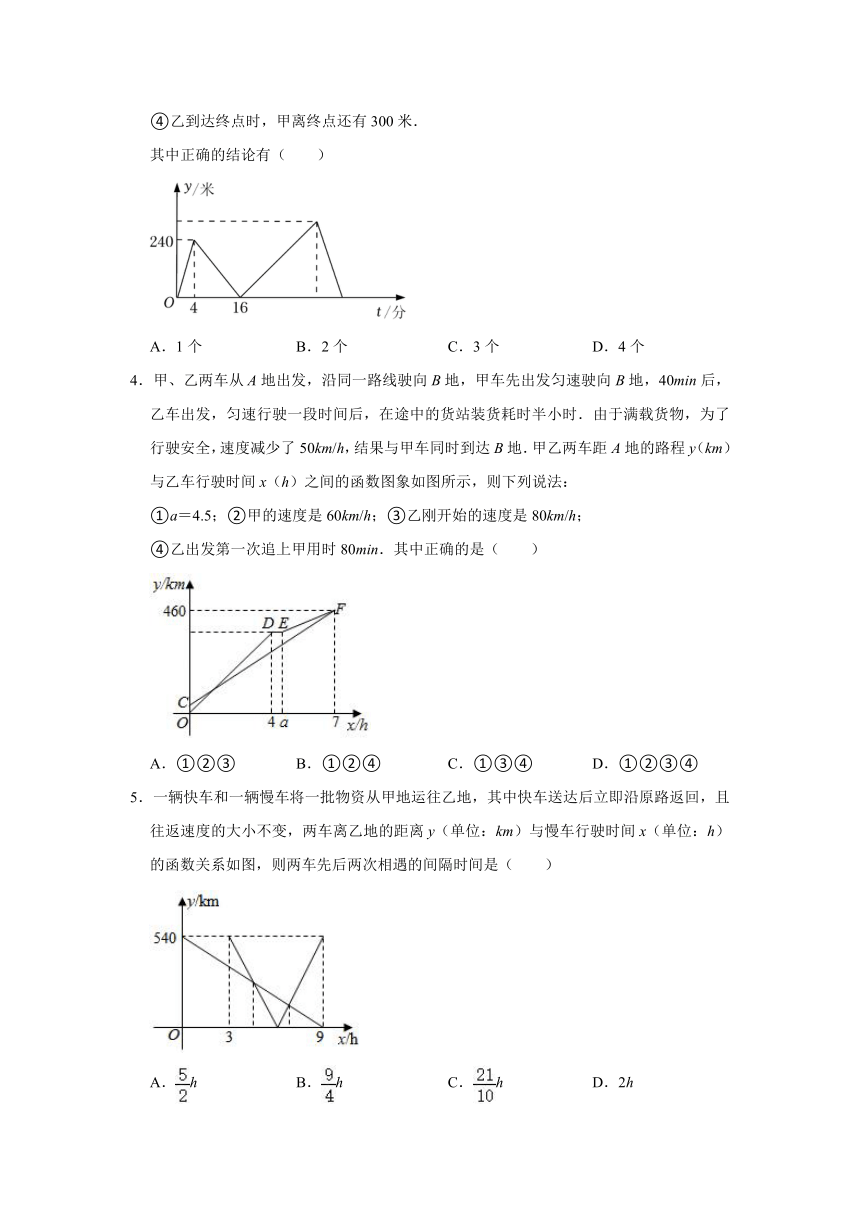
1.速度分别为100km/h和akm/h(0<a<100)的两车分别从相距s千米的两地同时出发,沿同一方向匀速前行.行驶一段时间后,其中一车按原速度原路返回,直到与另一车相遇时两车停止.在此过程中,两车之间的距离y(km)与行驶时间t(h)之间的函数关系如图所示.下列说法:
①a=60;②b=2;③c=b+;④若s=40,则b=.其中说法正确的是( )
A.①②③ B.①④ C.①② D.①③
2.小明和小李住在同一个小区,暑假期间,他们相约去缙云山某地露营;小明先出发5分钟后,小李以65米/分的速度从小区出发,小明到达相约地点后放下装备,休息了10分钟,立即按原路以另一速度返回,途中与小李相遇,随后他们一起步行到达目的地.小李与小明之间的距离y(米)与小明出发的时间x(分)之间的关系如图,则下列说法正确的是( )
A.小明首次到达目的地之前的速度是75米/分
B.小明首次到达目的地时,小李距离目的地还有200米
C.从小区到目的地路程为2800米
D.小明返回时的速度是33米/分
3.甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分)之间的关系如图所示,下列结论:
①甲步行的速度为60米/分;
②乙走完全程用了36分钟;
③乙用16分钟追上甲;
④乙到达终点时,甲离终点还有300米.
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
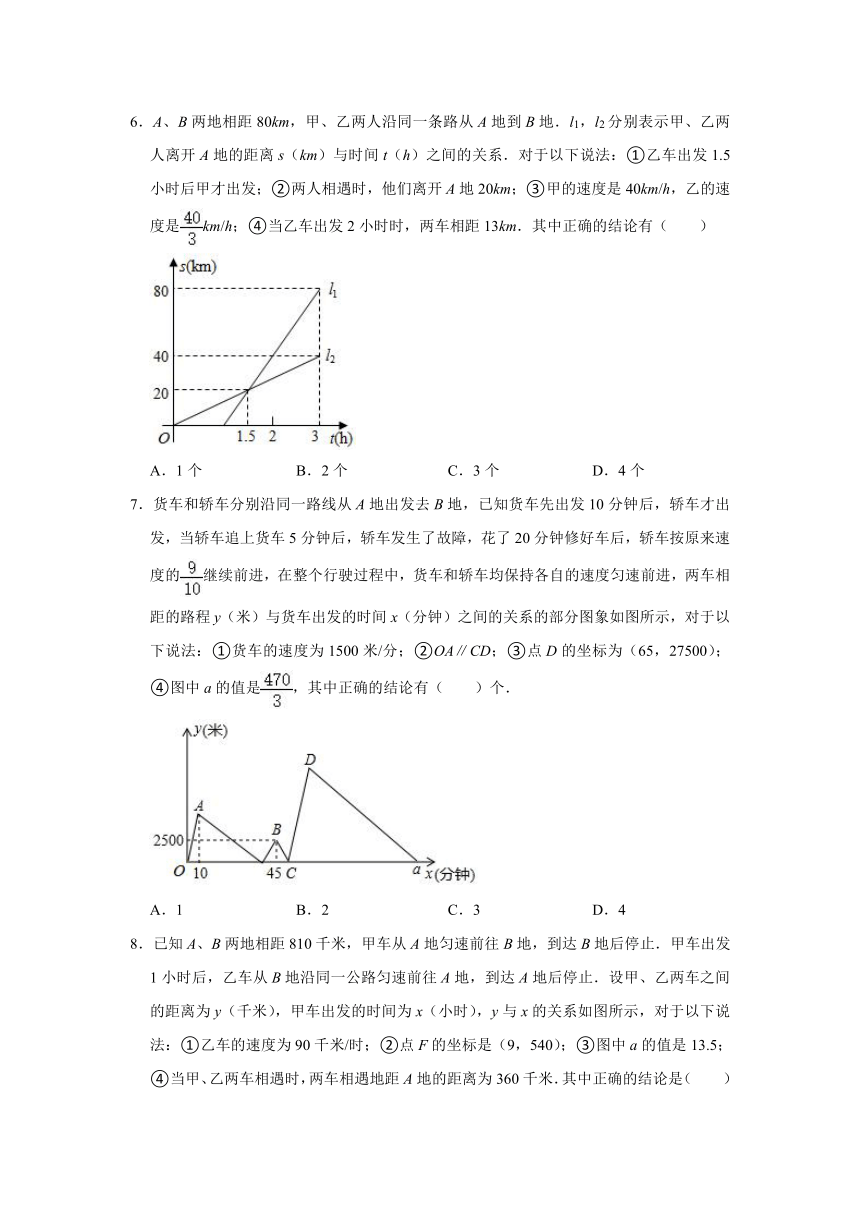
4.甲、乙两车从A地出发,沿同一路线驶向B地,甲车先出发匀速驶向B地,40min后,乙车出发,匀速行驶一段时间后,在途中的货站装货耗时半小时.由于满载货物,为了行驶安全,速度减少了50km/h,结果与甲车同时到达B地.甲乙两车距A地的路程y(km)与乙车行驶时间x(h)之间的函数图象如图所示,则下列说法:
①a=4.5;②甲的速度是60km/h;③乙刚开始的速度是80km/h;
④乙出发第一次追上甲用时80min.其中正确的是( )
A.①②③ B.①②④ C.①③④ D.①②③④
5.一辆快车和一辆慢车将一批物资从甲地运往乙地,其中快车送达后立即沿原路返回,且往返速度的大小不变,两车离乙地的距离y(单位:km)与慢车行驶时间x(单位:h)的函数关系如图,则两车先后两次相遇的间隔时间是( )
A.h B.h C.h D.2h
6.A、B两地相距80km,甲、乙两人沿同一条路从A地到B地.l1,l2分别表示甲、乙两人离开A地的距离s(km)与时间t(h)之间的关系.对于以下说法:①乙车出发1.5小时后甲才出发;②两人相遇时,他们离开A地20km;③甲的速度是40km/h,乙的速度是km/h;④当乙车出发2小时时,两车相距13km.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
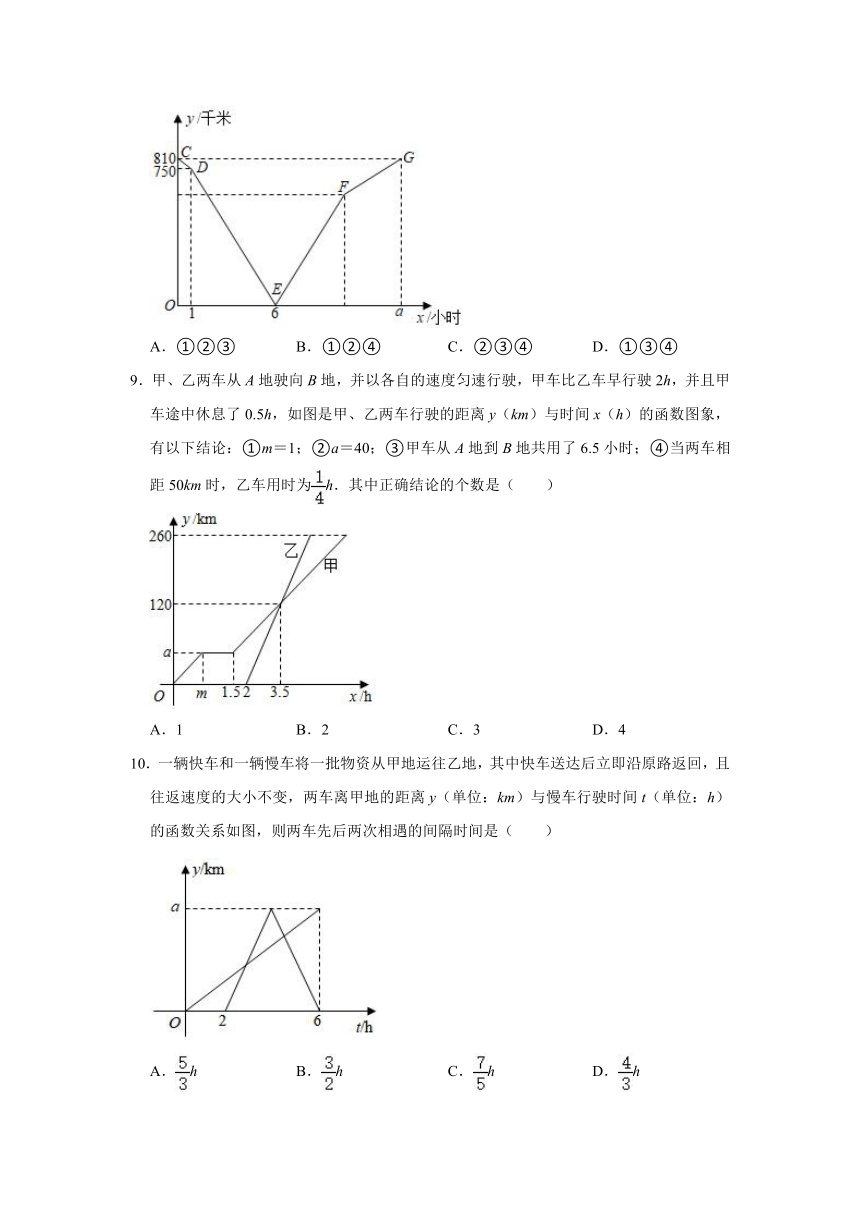
7.货车和轿车分别沿同一路线从A地出发去B地,已知货车先出发10分钟后,轿车才出发,当轿车追上货车5分钟后,轿车发生了故障,花了20分钟修好车后,轿车按原来速度的继续前进,在整个行驶过程中,货车和轿车均保持各自的速度匀速前进,两车相距的路程y(米)与货车出发的时间x(分钟)之间的关系的部分图象如图所示,对于以下说法:①货车的速度为1500米/分;②OA∥CD;③点D的坐标为(65,27500);④图中a的值是,其中正确的结论有( )个.
A.1 B.2 C.3 D.4
8.已知A、B两地相距810千米,甲车从A地匀速前往B地,到达B地后停止.甲车出发1小时后,乙车从B地沿同一公路匀速前往A地,到达A地后停止.设甲、乙两车之间的距离为y(千米),甲车出发的时间为x(小时),y与x的关系如图所示,对于以下说法:①乙车的速度为90千米/时;②点F的坐标是(9,540);③图中a的值是13.5;④当甲、乙两车相遇时,两车相遇地距A地的距离为360千米.其中正确的结论是( )
A.①②③ B.①②④ C.②③④ D.①③④
9.甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h,如图是甲、乙两车行驶的距离y(km)与时间x(h)的函数图象,有以下结论:①m=1;②a=40;③甲车从A地到B地共用了6.5小时;④当两车相距50km时,乙车用时为h.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
10.一辆快车和一辆慢车将一批物资从甲地运往乙地,其中快车送达后立即沿原路返回,且往返速度的大小不变,两车离甲地的距离y(单位:km)与慢车行驶时间t(单位:h)的函数关系如图,则两车先后两次相遇的间隔时间是( )
A.h B.h C.h D.h
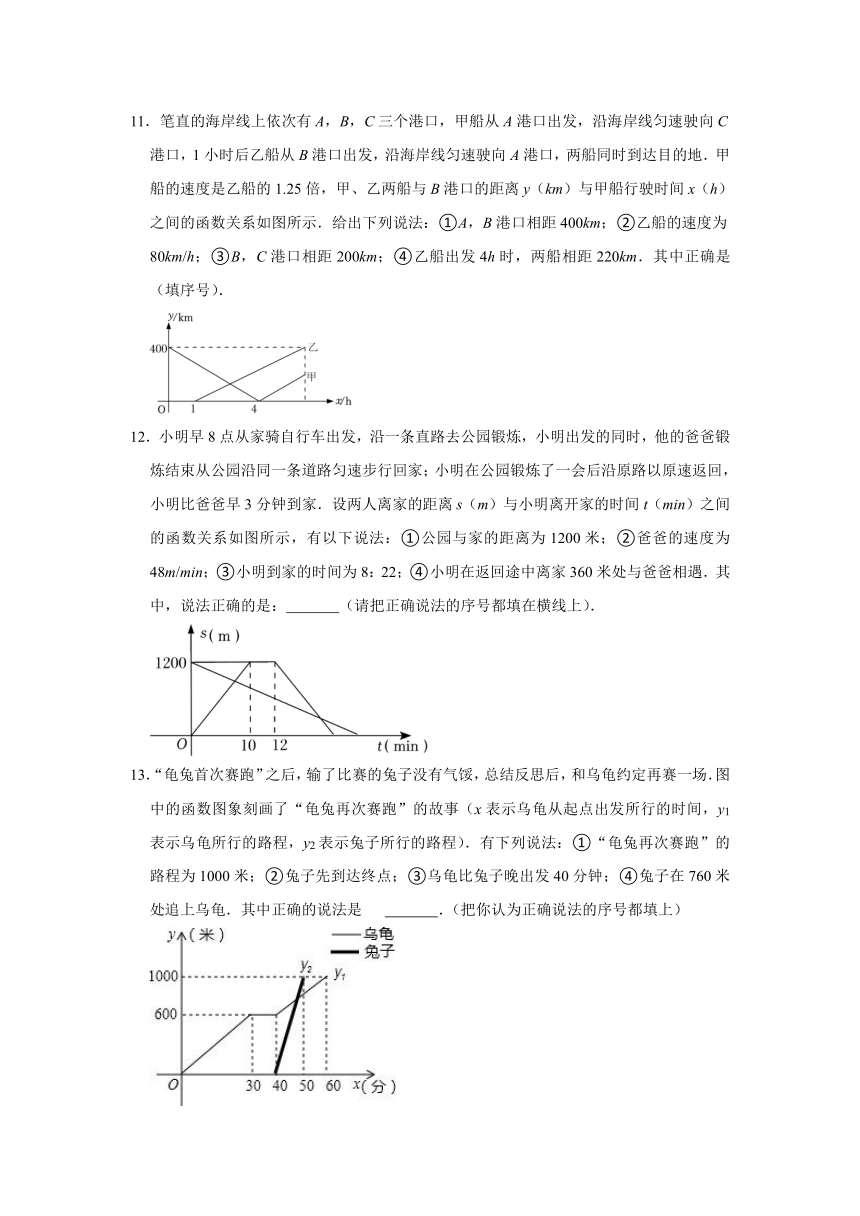
11.笔直的海岸线上依次有A,B,C三个港口,甲船从A港口出发,沿海岸线匀速驶向C港口,1小时后乙船从B港口出发,沿海岸线匀速驶向A港口,两船同时到达目的地.甲船的速度是乙船的1.25倍,甲、乙两船与B港口的距离y(km)与甲船行驶时间x(h)之间的函数关系如图所示.给出下列说法:①A,B港口相距400km;②乙船的速度为80km/h;③B,C港口相距200km;④乙船出发4h时,两船相距220km.其中正确是 (填序号).
12.小明早8点从家骑自行车出发,沿一条直路去公园锻炼,小明出发的同时,他的爸爸锻炼结束从公园沿同一条道路匀速步行回家;小明在公园锻炼了一会后沿原路以原速返回,小明比爸爸早3分钟到家.设两人离家的距离s(m)与小明离开家的时间t(min)之间的函数关系如图所示,有以下说法:①公园与家的距离为1200米;②爸爸的速度为48m/min;③小明到家的时间为8:22;④小明在返回途中离家360米处与爸爸相遇.其中,说法正确的是: (请把正确说法的序号都填在横线上).
13.“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程).有下列说法:①“龟兔再次赛跑”的路程为1000米;②兔子先到达终点;③乌龟比兔子晚出发40分钟;④兔子在760米处追上乌龟.其中正确的说法是 .(把你认为正确说法的序号都填上)
14.小明和小杰在同一直道的A,B两点间作匀速往返走锻炼(忽略掉头等时间).小明从A地出发,同时小杰从B地出发,两人第一次相遇时小明曾停下接电话数分钟.图中的折线表示从开始到小杰第一次到达A地止,两人之间的距离y(米)与行走时间x(分)的函数关系图象.则图中的b= 米,d= 分.
15.甲、乙两车分别从A、B两地同时出发,沿同一条公路相向而行,相遇时甲、乙所走路程的比为2:3,甲、乙两车离AB中点C的路程y(千米)与甲车出发时间t(时)的关系图象如图所示,则下列说法
①乙车的速度为90千米/时;
②a的值为;
③b的值为150;
④当甲、乙车相距30千米时,甲行走了h或h.
正确的是 .
16.甲、乙两车从A地驶向B地,甲车比乙车早行驶2h,并且在途中休息了0.5h,休息前后速度相同,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.则下列结论正确的是 .
①a的值为40;
②当1.5<x≤7时,甲车行驶路程y与时间x的函数表达式为y=40x﹣20;
③乙车比甲车早1.5h到达B地;
④乙车行驶0.5h或2.5h时,两车恰好相距40km.
17.甲、乙两人相约周末沿同一条路线登山,甲、乙两人距地面的高度y(米)与登山时间x(分钟)之间的函数图象如图所示,根据图象所提供的信息解答下列问题.
(1)甲登山的速度是多少?
(2)乙到达A地后决定提速,提速后乙的速度是甲登山速度的3倍,求乙登山全过程中,登山时距地面的高度y(米)与登山时间x(分钟)之间的函数解析式;
(3)在(2)的条件下,当x为多少时,甲、乙两人距地面的高度差为80米?
18.如图,在平面直角坐标系中,一次函数y=﹣x+b的图象与x轴,y轴分别交于B,C两点,与正比例函数y=x的图象交于点A,点A的横坐标为4.
(1)求A,B,C三点的坐标;
(2)若动点M在线段OA上运动,当三角形OMC的面积是三角形OAC的面积的时,求点M的坐标;
(3)若点P(m,1)在三角形AOB的内部(不包括边界),求m的取值范围.
19.已知A、B两地间有C地,客车由A地驶向C地,货车由B地经过C地去A地(客货车在A、C两地间沿同一条路行驶),两车同时出发,匀速行驶.货车的速度是客车速度的.如图是客车、货车离C站的路程y(km)与行驶时间x(h)的函数关系图象.
(1)求货车的速度并求A、B两地间的路程.
(2)求客车y与x的函数关系式并直接写出货车y与x的函数关系式.
(3)求点P的坐标并说出点P的实际意义.
(4)出发后经过多长时间两车间路程是70km?
20.如图,在平面直角坐标系中,O为坐标原点,已知直线y=﹣x+8与x轴、y轴分别交于B、A两点.直线OD⊥直线AB于点D.现有一点P从点D出发,沿线段DO向点O运动,另一点Q从点O出发,沿线段OA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到O时,两点都停止.设运动时间为t秒.
(1)点A的坐标为 .
(2)设△OPQ的面积为S,问当t为何值时S的值最大?最大值是多少?
(3)是否存在某一时刻t,使得△OPQ为等腰三角形?若存在,直接写出所有满足条件的t的值;若不存在,则说明理由.
21.甲、乙两车分别从B,A两地同时出发,甲车匀速前往A地;乙车匀速前往B地,到达B地立即以另一速度按原路匀速返回到A地;设甲、乙两车距A地的路程为y(千米),乙车行驶的时间为x(时),y与x之间的函数图象如图所示.
(1)求乙车从B地到达A地的速度;
(2)求乙车到达B地时甲车距A地的路程;
(3)求乙车返回前甲、乙两车相距40千米时,乙车行驶的时间.
22.如图,在平面直角坐标系中,直线AB:y=﹣x+3,与x轴,y轴交于点A、B,直线x=﹣1与直线AB交于点D,直线l过点A,与y轴交于点C,点C的纵坐标是﹣.
(1)求直线AC的解析式;
(2)在直线l上是否存在点P,点P在直线x=﹣1的左侧,使得S△ABC=S△PDB,若存在,请求出点P的坐标,若不存在,请说明理由.
(3)在第(2)问的条件下,点Q是线段PD的动点,过点Q做QM∥x轴,交直线AB与点M,在x轴上是否存在点N,使得△QMN为等腰直角三角形,若存在,请直接写出点N的坐标,若不存在,请说明理由.
23.如图,在平面直角坐标系中,O为坐标原点,一次函数y=x+4与x轴,y轴分别交于点B,点A,点C的坐标为C(5,0),点P是射线BO上一动点.
(1)点A的坐标是 ;点B的坐标是 ;
(2)连接AP,若△ABP的面积为10,求点P的坐标;
(3)当点P在射线BO上运动时,若△APC是等腰三角形,请直接写出点P的坐标.
24.在一条笔直的公路旁依次有A、B、C三个村庄,甲、乙两人同时分别从A、B两村出发,甲骑摩托车,乙骑电动车沿公路匀速驶向C村,最终到达C村.设甲、乙两人到C村的距离y1,y2(km)与行驶时间x(h)之间的函数关系如图所示,请回答下列问题.
(1)A,C两村间的距离为 km,a= .
(2)求出图中点P的坐标,并解释该点坐标所表示的实际意义.
(3)乙在行驶过程中,何时距甲20km.
25.某剧院举行新年专场音乐会,成人票每张40元,学生票每张10元,剧院制定了两种优惠方案,且每个团体购票时只能选择其中一种优惠方案,方案1:购买一张成人票赠送一张学生票;方案2:按总价的90%付款.某校有4名老师与x(x≥4)名学生去观赏这次音乐会,设用方案1和方案2付款的总金额分别为y1(元)和y2(元).
(1)分别求出y1、y2与x之间的函数关系式;
(2)当学生人数为20名时,请通过计算说明哪种方案更优惠;
(3)请通过计算说明:当学生人数为多少时,选择两种方案一样优惠?
26.为全面打造“艺美郓城”美育品牌,逐步形成具有郓城特色的美育体系.某校学生展示花鼓表演,在笔直的跑道两端有A、B两地相距240米,甲队从A地跑到B地,乙队从B地跑到A地.已知乙队的速度是甲队的2倍,两队同时出发,乙队到达A地后12分钟甲队到达B地.
(1)求甲队每分钟跑 米;
(2)如图表示的是甲、乙两队离B地的距离S(米)与时间t(分钟)之间的函数图象,请分别求出甲、乙两队的函数关系式,并求出甲、乙两队相遇时t的值;
(3)求甲、乙两队相距30米时t的值.
27.小明家、新华书店、学校在一条笔直的公路旁,某天小明骑车上学,当他骑了一段后,想起要买某本书,于是又返回到刚经过的新华书店,买到书后继续骑车去学校,他本次骑车上学的过程中离家距离与所用的时间的关系如图所示,请根据图象提供的信息回答下列问题:
(1)小明家到学校的距离是 米;小明在书店停留了 分钟;
(2)如果骑车的速度超过了300米/分就超越了安全限度,小明买到书后继续骑车到学校的这段时间的骑车速度在安全限度内吗?请说明理由;
(3)请直接写出小明出发后多长时间离家的距离为900米?
28.A、B两地相距60km,甲、乙两人从两地出发相向而行,甲先出发,图中l1,l2表示两人离A地的距离s(km)与时间t(h)的关系,请结合图象解答下列问题:
(1)表示乙离A地的距离与时间关系的图象是 (填“l1”或“l2”);甲的速度是 km/h,乙的速度是 km/h.
(2)甲出发多长时间两人相遇?
(3)甲出发多长时间后两人恰好相距5km?
参考答案
1.解:①两车的速度之差为80÷(b+2﹣b)=40(km/h),
∴a=100﹣40=60,结论①正确;
②两车第一次相遇所需时间=(h),
∵s的值不确定,
∴b值不确定,结论②不正确;
③两车第二次相遇时间为b+2+=b+(h),
∴c=b+,结论③正确;
④∵b=,s=40,
∴b=1,结论④不正确.
故选:D.
2.解:小明首次到达目的地之前的速度是=80(米/分),
故A不正确;
两地间的距离为:80×35=2800(米),
小李在小明到达目的地时行走的路程为:65×(35﹣5)=65×30=1950(米),
∴2800﹣1950=850(米),
此时,小李距目的地还有850米,
故B不正确;C正确;
D、850﹣65×10=200(米),200÷(47﹣45)=100(米/分),100﹣65=35(米/分),
故D不正确;
故选:C.
3.解:由题意可得:甲步行速度==60(米/分);
故①结论正确;
设乙的速度为:x米/分,
由题意可得:16×60=(16﹣4)x,
解得x=80,
∴乙的速度为80米/分;
∴乙走完全程的时间==30(分),
故②结论错误;
由图可得,乙追上甲的时间为:16﹣4=12(分);
故③结论错误;
乙到达终点时,甲离终点距离是:2400﹣(4+30)×60=360(米),
故④结论错误;
故正确的结论有①共1个.
故选:A.
4.解:由图象可得,
a=4+0.5=4.5,故①正确;
甲的速度是460÷(7+)=60(km/h),故②正确;
设乙刚开始的速度是vkm/h,则后来的速度为(v﹣50)km/h,
4v+(7﹣4.5)×(v﹣50)=460,
解得v=90,故③错误;
设乙出发第一次追上甲用时th,
90t=60(t+),
解得t=,
h=80min,故④正确;
故选:B.
5.解:根据图象可知,慢车的速度为=60(km/h).
对于快车,由于往返速度大小不变,总共行驶时间是(9﹣3)h,
故其速度为=180(km/h).
所以对于慢车,y与t的函数表达式为y=540﹣60x (0≤x≤9)①.
对于快车,设当3≤x≤6时,y与x的函数表达式为y=kx+b,
由题意得:,
解得:,
∴对于快车,当3≤x≤6时,y与x的函数表达式为y=﹣180x+1080②,
对于快车,设当6<x≤9时,y与x的函数表达式为y=kx+b,
由题意得:,
解得:,
∴对于快车,当3≤x≤6时,y与x的函数表达式为y=180x﹣1080③,
联立①②,可解得交点横坐标为x=,
联立①③,可解得交点横坐标为x=,
因此,两车先后两次相遇的间隔时间是﹣=(h),
故选:B.
6.解:由图象可得,
乙车出发1.5小时后甲乙相遇,故①错误;
两人相遇时,他们离开A地20km,故②正确;
甲的速度是(80﹣20)÷(3﹣1.5)=40(km/h),乙的速度是km/h,故③正确;
当乙车出发2小时时,两车相距:20+(2﹣1.5)×40﹣×2=km,故④错误;
故选:B.
7.解:①由图象可知,当x=10时,轿车开始出发;当x=45时,轿车开始发生故障,则x=45﹣5=40(分钟),即货车出发40分钟时,轿车追上了货车,
设货车,轿车的速度分别为m米/分,n米/分,
根据题意,得,
解得,
所以货车的速度为1500米/分,故①正确;
②由题意可知,OA段货车在行驶,轿车停止;CD段货车在行驶,轿车发生故障停止,
则OA与x轴夹角和CD与x轴夹角相等,所以OA∥CD,故②正确;
③轿车故障花了20分钟修好,由题意图象可知,B点时x=45,此时轿车开始分钟故障,D点时轿车刚修好,即此时x=45+20=65,
∴D点纵坐标为:(20﹣)×1500=30000﹣2500=27500,
∴D点坐标为:(65,27500),故③正确;
④在D点时,轿车的速度变为原来的,
即此时轿车的速度为:2000×=1800(米/分),
D点坐标为:(65,27500),到x=a时轿车开始追赶货车直到两车相遇,
∴(a﹣65)×(1800﹣1500)=27500,
解得a=65+=,
即图中a的值是,故④正确.
综上所述,正确的结论①②③④.
故选:D.
8.解:由图象可知,
甲车行驶的速度为(810﹣750)÷1=60(千米/时),
设乙车的速度为x千米/时,根据题意得:
6×60+(6﹣1)x=810,
解得x=90.
即乙车的速度为90千米/时,故①正确;
乙车从B地到达A地的时间为810÷90=9(小时),
∵甲车出发1小时后,乙车从B地沿同一公路匀速前往A地,
∴甲车行驶的时间为9+1=10(小时),
∴甲车10小时行驶的路程为60×10=600(千米),
∴点F的坐标为(10,600),故②错误;
甲车从A地匀速前往B地的时间为810÷60=13.5(小时),
∴a=13.5,故③正确;
当甲、乙两车相遇时,甲车行驶了6小时,
行驶的路程为60×6=360(千米),故④正确,
综上,正确的结论是①③④,
故选:D.
9.解:由题意,得m=1.5﹣0.5=1,故①结论正确;
120÷(3.5﹣0.5)=40(km/h),则a=40,故②结论正确;
设甲车休息之后行驶路程y(km)与时间x(h)的函数关系式为y=kx+b,由题意,得:
,
解得,
∴y=40x﹣20(1.5<x≤7),
当y=260时,260=40x﹣20,
解得:x=7,
∴甲车从A地到B地共用了7小时,故③结论错误;
当1.5<x≤7时,y=40x﹣20.
设乙车行驶的路程y与时间x之间的解析式为y=k'x+b',由题意得:
,
解得,
∴y=80x﹣160.
当40x﹣20﹣50=80x﹣160时,
解得:x=,
当40x﹣20+50=80x﹣160时,
解得:x=,
∴﹣2=,﹣2=,
所以乙车行驶小时或小时,两车恰好相距50km,故④结论错误.
∴正确结论的个数是2个.
故选:B.
10.解:根据图象可知,慢车的速度为.
对于快车,由于往返速度大小不变,总共行驶时间是4 h,
因此单程所花时间为2 h,故其速度为.
所以对于慢车,y与t的函数表达式为①.
对于快车,y与t的函数表达式为y=,
联立①②,可解得交点横坐标为t=3,
联立①③,可解得交点横坐标为t=4.5,
因此,两车先后两次相遇的间隔时间是1.5,
故选:B.
11.解:由题意和图象可知,
A、B港口相距400km,故①正确;
∵甲船4个小时行驶了400km,
∴甲船的速度为:400÷4=100(km/h),
∵甲船的速度是乙船的1.25倍,
∴乙船的速度为:100÷1.25=80(km/h),
故②正确;
∵乙船的速度为80km/h,
∴400÷80=(400+sBC)÷100﹣1,
解得:sBC=200km,
故③正确;
乙出发4h时两船相距的距离是:4×80+(4+1﹣4)×100=420(km),
故④错误.
故答案为:①②③.
12.解:由图象可得,
公园与家的距离为1200米,故①正确;
爸爸的速度为:1200÷(12+10+3)=48(m/min),故②正确;
∵10+12+10=22(min),
∴小明到家的时间为8:22,故③正确;
小明的速度为:1200÷10=120(m/min),
设小明在返回途中离家a米处与爸爸相遇,
=12+,
解得,a=240,
即小明在返回途中离家240米处与爸爸相遇,故④不正确;
故答案为:①②③.
13.解:由函数图象可得,
“龟兔再次赛跑”的路程为1000米,故①说法正确;
兔子先到达终点,故②说法正确;
兔子比乌龟晚出发40分钟,故③说法错误;
当40≤x≤60时,设y1与x的函数关系式为y1=kx+b,
∵点(40,600),(60,1000)在该函数图象上,
∴,
解得,
∴当40≤x≤60时,y1与x的函数关系式为y1=20x﹣200;
当40≤x≤50时,设y2与x的函数关系式为y2=mx+n,
∵点(40,0),(50,1000)在该函数图象上,
∴,
解得,
即当40≤x≤50时,y2与x的函数关系式为y2=100x﹣4000;
令20x﹣200=100x﹣4000,
解得x=47.5,
∴当x=47.5时,此时y1=y2=750,
即兔子在750米处追上乌龟,故④错误;
故答案为:①②.
14.解:由折线可知小杰的速度为:4200÷70=60米/分,
且=60,
解得c=30,
则两人速度和为4200÷30=140米/分,故小明速度为:140﹣60=80米/分,
d点表示小明到达B地开始返向,
4200=30×80+(d﹣40)×80,
得d=62.5,
则a=62.5×60=3750,
b=3750﹣(80﹣60)×7.5=3600.
故答案为:3600,62.5.
15.解:①A、B两地之间的距离为30×2÷(﹣)=300(千米),
∴出发时,甲、乙两车离AB中点C的路程是300÷2=150(千米),即b=150,③正确;
②乙车的速度为(150+30)÷2=90(千米/小时),①正确;
③甲车的速度为(150﹣30)÷2=60(千米/小时),
∴a的值为150÷60=,③正确;
④设出发xh甲、乙车相距30千米,
则(90+60)x=300﹣30或(90+60)x=300+30,
解得:x=或x=,故④错误.
综上所述:正确的结论有①②③.
故答案为:①②③.
16.解:a=120÷(3.5﹣0.5)×1=40,故①正确;
当1.5<x≤7时,设甲车行驶路程y与时间x的函数表达式为y=kx+b,
,得,
即当1.5<x≤7时,甲车行驶路程y与时间x的函数表达式为y=40x﹣20,故②正确;
乙车的速度为:120÷(3.5﹣2)=80(km/h),
乙车从A地到B地用的时间为:260÷80=3.25(h),
乙车比甲车早[3.5+(260﹣120)÷40]﹣(2+3.25)=1.75h到达B地,故③错误;
当乙车行驶0.5h时,两车相距[40+(2+0.5﹣1.5)×40]﹣80×0.5=40(km),
当乙车行驶2.5h时,两车相距80×2.5﹣[40+(2﹣1.5+2.5)×40]=40(km),
故④正确;
故答案为:①②④.
17.解:(1)甲登山的速度为:(300﹣100)÷20=10(米/分),
答:甲登山的速度是10米/分;
(2)V乙=3V甲=30米/分,
t=2+(300﹣30)÷30=11(分钟),
设2到11分钟,乙的函数解析式为y=kx+b,
∵直线经过A(2,30),(11,300),
∴,
解得,
∴当2<x≤11时,y=30x﹣30,
设当0≤x≤2时,乙的函数关系式为y=ax,
∵直线经过A(2,30),
∴30=2a解得a=15,
∴当0≤x≤2时,y=15x,
综上,y=;
(3)设甲的函数解析式为:y=mx+100,将(20,300)代入得:300=20m+100,
∴m=10,
∴y=10x+100.
∴当0≤x≤2时,由(10x+100)﹣15x=80,解得x=4>2矛盾,故此时没有符合题意的解;
当2<x≤11时,由|(10x+100)﹣(30x﹣30)|=80得,
|130﹣20x|=80,
∴x=2.5或x=10.5;
当11<x≤20时,由300﹣(10x+100)=80得x=12,
∴x=2.5或10.5或12.
∴当x为2.5或10.5或12时,甲、乙两人距地面的高度差为80米.
18.解:(1)∵点A在正比例函数y=x的图象上,且点A的横坐标为4.
∴点A(4,2),
∵一次函数y=﹣x+b的图象与正比例函数y=x的图象交于点A,
∴2=﹣4+b,
∴b=6,
∴一次函数解析式为y=﹣x+6,
∵一次函数y=﹣x+6的图象与x轴,y轴分别交于B,C两点,
∴点B(6,0),点C(0,6);
(2)由(1)可知:OC=6,xA=4,
∴S△OAC=×OC×xA=×6×4=12,
∵S△OMC=S△OAC=4,
∴S△OMC=×OC×|xM|=4,
∴|xM|=,
∴xM=±,
当动点M在线段OA上时,x>0,则当x=时,y=×=,
∴此时M点的坐标为(,);
(3)∵点P(m,1)在△AOB的内部(不包括边界),
∴当y=1时,代入正比例函数中得:1=x,
解得:x=2,
当y=1时,代入一次函数中得:1=﹣x+6,
解得:x=5,
∴2<m<5.
故答案为:2<m<5.
19.解:(1)由图象可得,
客车的速度:720÷9=80(km/h),
则货车速度:(km/h).
A与B两地间路程为:60×2+720=840(km),
即货车的速度是60km/h,A、B两地间的路程是840km;
(2)设客车y与x的函数关系式是y=kx+b,
,
解得,
即客车y与x的函数关系式是y=﹣80x+720;
当0≤x≤2时,设货车y与x的函数关系式是y=ax+c,
∵货车的速度为60km/h,60×2=120,
∴该函数过点(0,120),(2,0),
∴,
解得,
即当0≤x≤2时,货车y与x的函数关系式是y=﹣60x+120;
720÷60=12,
当2<x≤14时,设货车y与x的函数关系式是y=mx+n,
∵点(2,0),(14,720)在该函数图象上,
∴,
解得,
即当2<x≤14时,货车y与x的函数关系式是y=60x﹣120;
由上可得,货车y与x的函数关系式是y=;
(3)令﹣80x+720=60x﹣120,
解得x=6,
则x=6时,y=60×6﹣120=360﹣120=240,
∴点P的坐标为(6,240),
点P的实际意义是:两车出发6小时,两车相遇.与C地相距240km;
(4)当两车相遇前相距70千米时,
(﹣80x+720)﹣(60x﹣120)=70,
解得x=5.5,
当两车相遇后相距70千米时,
(60x﹣120)﹣(80x+720)=70,
解得x=6.5,
综上所述,出发后经过5.5小时或6.5小时,两车相距70千米.
20.解:(1)y=﹣x+8与x轴、y轴分别交于B、A两点,
令x=0,则y=8,
∴A(0,8),
故答案为:(0,8);
(2)∵A(0,8),
∴OA=8,
令y=0,则﹣x+8=0,
∴x=6,
∴B(6,0),
∴OB=6,
∴AB=10,
∵OD⊥AB,
∴S△AOB=OA×OB=AB×OD,
∴OD==,
如图,过点P作PH⊥OA于H,
在Rt△AOD中,OA=8,OD=,
根据勾股定理得,AD=,
由运动知,DP=t,OQ=t,
∴OP=OD﹣DP=﹣t,
∴PH=(﹣t)×,
∴t=时,S最大,最大值为;
(3)∵△OPQ为等腰三角形,
∴①当OQ=OP时,
∴t=﹣t,
∴t=,
②当OQ=PQ时,在Rt△AOD中
如图,过点Q作QM⊥OD于M,
∴OM=OP=(﹣t),
在Rt△OMQ中,OM=t,
∴(﹣t)=t,
∴t=,
③当PO=PQ时,如图,
过点P作PH⊥OA于H,
∴OH=OQ=t,
在Rt△POH中,OH=(﹣t),
∴t=(﹣t),
∴t=,
∴△OPQ为等腰三角形时,t的值为秒或秒或秒.
21.解:(1)由图象可得,
乙车从A地到B地的速度为:180÷1.5=120(千米/时),
∴120m=300,
解得m=2.5,
∴乙车从B地到达A地的速度为:300÷(5.5﹣2.5)=300÷3=100(千米/时),
即乙车从B地到达A地的速度是100千米/时;
(2)由图象可得,
甲车的速度为:(300﹣180)÷1.5=120÷1.5=80(千米/时),
则乙车到达B地时甲车距A地的路程是:300﹣2.5×80=300﹣200=100(千米),
即乙车到达B地时甲车距A地的路程是100千米;
(3)乙车返回前甲、乙两车相距40千米时,设乙车行驶的时间为t小时,
甲乙相遇之前:80t+120t+40=300,
解得t=1.3;
甲乙相遇之后:80t+120t﹣40=300,
解得t=1.7;
答:乙车返回前甲、乙两车相距40千米时,乙车行驶的时间是1.3小时或1.7小时.
22.解:(1)在y=﹣x+3中,令x=0得y=3,令y=0得x=3,
∴A(3,0),B(0,3),
∵点C的纵坐标是﹣,
∴C(0,﹣),
设直线AC的解析式为y=kx﹣,把A(3,0)代入得:
0=3k﹣,解得k=,
∴直线AC的解析式为y=x﹣;
(2)在直线l上存在点P,使得S△ABC=S△PDB,
设PB交直线x=﹣1于E,如图:
∵A(3,0),B(0,3),C(0,﹣),
∴S△ABC=BC OA=×(3+)×3=,
在y=﹣x+3中,令x=﹣1得y=4,
∴D(﹣1,4),
设P(m,m﹣),直线PB为y=k'x+3,
则m﹣=k'm+3,解得k'=,
∴直线PB为y=x+3,
令x=﹣1得y=,
∴E(﹣1,),
∴DE=4﹣=,
∵S△ABC=S△PDB,
∴DE |xB﹣xP|=,即××(﹣m)=,
解得m=﹣6,
∴P(﹣6,﹣);
(3)在x轴上存在点N,使得△QMN为等腰直角三角形,
由P(﹣6,﹣),D(﹣1,4)得直线PD解析式为y=x+,
设Q(t,t+),
∵QM∥x轴,M在AB上,
∴在y=﹣x+3中令y=t+,得x=﹣t﹣,
∴M(﹣t﹣,t+),
∴QM=﹣t﹣﹣t=﹣,
①当Q为直角顶点时,如图:
∵QM=QN,
∴﹣=t+,
解得t=﹣,
∴N(﹣,0);
②当M为直角顶点时,如图:
∵QM=MN,
∴﹣=t+,
解得t=﹣,
∴N(,0);
③当N为直角顶点时,过N作NH⊥QM,如图:
∵QM=2NH,
∴﹣=2×(t+),
解得t=﹣,
∴Q(﹣,),
∴QH=NH=,
∴ON=﹣=,
∴N(﹣,0);
综上所述,N的坐标为:(﹣,0)或(,0)或(﹣,0).
23.解:(1)在y=x+4中,令y=0,
得x+4=0,
解得:x=﹣8,
∴B(﹣8,0),
令x=0,得y=4,
∴A(0,4),
故答案为:(0,4),(﹣8,0);
(2)∵S△ABP=BP OA=10,
∴×BP×4=10,
∴BP=5,
∴PO=3,
∵点P是射线BO上一动点,
∴P(﹣3,0);
(3)设P(x,0),
①若AP=AC,
∴x2+42=42+52,
∴x=﹣5,x=5(舍去),
∴P(﹣5,0);
②若AC=PC,
∴(5﹣x)2=42+52,
∴x=5+或x=5﹣,
∴P(5+,0)或P(5﹣,0);
③若AP=PC,
∴x2+42=(x﹣5)2,
∴x=,
∴P(,0).
综合以上可得,点P的坐标为(﹣5,0)或(5+,0)或P(5﹣,0)或(,0).
24.解:(1)A、C两村间的距离120km,
a=120÷[(120﹣90)÷0.5]=2;
故答案为120,2;
(2)设y2=k2x+90,
代入(3,0),得0=3k2+90,
解得k2=﹣30,
所以y2=﹣30x+90.
当y1=y2时,
﹣60t+120=﹣30t+90,
解得:t=1,
所以甲乙二人行驶1小时后两人相遇,
此时距离C村60km,
故P点坐标为P(1,60).
(3)当y1﹣y2=20,
即﹣60x+120﹣(﹣30x+90)=20
解得x=,
当y2﹣y1=20,
即﹣30x+90﹣(﹣60x+120)=20
解得x=,
当甲走到C地,而乙距离C地20km时,
﹣30x+90=20
解得x=;
综上所知当x=h,或x=h,或x=h乙距甲20km.
25.解:(1)由题意可得,
y1=4×40+10(x﹣4)=10x+120,
y2=(4×40+10x)×90%=9x+144;
(2)当x=20时,y1=10×20+120=320,
y2=9×20+144=324;
∵320元<324元,
∴当x=20时,方案一更优惠;
(3)令10x+120=9x+144,得x=24,
答:当学生为24人时,两种方案一样优惠.
26.解:(1)由图象可得,
甲队每分钟跑:240÷24=10(米),
故答案为:10;
(2)设甲队离B地的距离S(米)与时间t(分钟)之间的函数关系式为S=kt+b,
∵点(0,240),(24,0)在该函数图象上,
∴,
解得,
即甲队离B地的距离S(米)与时间t(分钟)之间的函数关系式为S=﹣10t+240(0≤t≤24);
设乙队离B地的距离S(米)与时间t(分钟)之间的函数关系式为S=at,
∵点(12,240)在该函数图象上,
∴240=12a,
解得a=20,
即乙队离B地的距离S(米)与时间t(分钟)之间的函数关系式为S=20t(0≤t≤12);
当甲和乙相遇时,﹣10t+240=20t,
解得t=8,
即甲、乙两队相遇时t的值是8;
(3)当甲和乙相遇前相距30米,
﹣10t+240﹣20t=30,
解得t=7;
当甲和乙相遇后相距30米,
∴20t﹣(﹣10t+240)=30,
解得t=9,
即甲、乙两队相距30米时t的值是7或9.
27.解:(1)根据图象,学校的纵坐标为1500,小明家的纵坐标为0,
故小明家到学校的路程是1500米;
根据题意,小明在书店停留的时间为从8分到12分,
故小明在书店停留了4分钟.
故答案为:1500;4;
(2)由图象可知:
12~14分钟时,平均速度==450米/分,
∵450>300,
∴小明买到书后继续骑车到学校,这段时间速度不在安全限度内;
(3)从图象上看,小明出发后离家距离为900米时,一共有三个时间,
①在0~6分钟时,平均速度为:=200米/分,
距家900米的时间为:t1=900÷200=4.5(分);
②在6~8分钟内,平均速度==300米/分,
距家900米时时间为t2,则:1200﹣300(t2﹣6)=900,
解得:t2=7,
③在12~14分钟内,平均速度450米/分,
距家900米时时间为t3,则600+450(t3﹣12)=900,
解得:t3=12,
综上,小明出发4.5分钟或7分钟或12分钟时距家900米.
28.解:(1)∵甲先出发,由图象可知l1,l2分别表示甲、乙的函数图象,
∴甲的速度为60÷2=30(km/h),乙的速度为60÷(3.5﹣0.5)=20(km/h),
故答案为l2,30,20;
(2)设甲出发xh后两人相遇,根据题意得:
30x+20(x﹣0.5)=60,
解得x=1.4,
∴甲出发1.4h后两人相遇;
(3)设甲出发th时后两人恰好相距5km,
①两人相遇前:
30t+20(t﹣0.5)+5=60,
解得t=1.3,
②两人相遇后:
30t+20(t﹣0.5)﹣5=60,
解得:t=1.5,
∴甲出发1.3h或1.5h时后两人恰好相距5km.
1.速度分别为100km/h和akm/h(0<a<100)的两车分别从相距s千米的两地同时出发,沿同一方向匀速前行.行驶一段时间后,其中一车按原速度原路返回,直到与另一车相遇时两车停止.在此过程中,两车之间的距离y(km)与行驶时间t(h)之间的函数关系如图所示.下列说法:
①a=60;②b=2;③c=b+;④若s=40,则b=.其中说法正确的是( )
A.①②③ B.①④ C.①② D.①③
2.小明和小李住在同一个小区,暑假期间,他们相约去缙云山某地露营;小明先出发5分钟后,小李以65米/分的速度从小区出发,小明到达相约地点后放下装备,休息了10分钟,立即按原路以另一速度返回,途中与小李相遇,随后他们一起步行到达目的地.小李与小明之间的距离y(米)与小明出发的时间x(分)之间的关系如图,则下列说法正确的是( )
A.小明首次到达目的地之前的速度是75米/分
B.小明首次到达目的地时,小李距离目的地还有200米
C.从小区到目的地路程为2800米
D.小明返回时的速度是33米/分
3.甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分)之间的关系如图所示,下列结论:
①甲步行的速度为60米/分;
②乙走完全程用了36分钟;
③乙用16分钟追上甲;
④乙到达终点时,甲离终点还有300米.
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
4.甲、乙两车从A地出发,沿同一路线驶向B地,甲车先出发匀速驶向B地,40min后,乙车出发,匀速行驶一段时间后,在途中的货站装货耗时半小时.由于满载货物,为了行驶安全,速度减少了50km/h,结果与甲车同时到达B地.甲乙两车距A地的路程y(km)与乙车行驶时间x(h)之间的函数图象如图所示,则下列说法:
①a=4.5;②甲的速度是60km/h;③乙刚开始的速度是80km/h;
④乙出发第一次追上甲用时80min.其中正确的是( )
A.①②③ B.①②④ C.①③④ D.①②③④
5.一辆快车和一辆慢车将一批物资从甲地运往乙地,其中快车送达后立即沿原路返回,且往返速度的大小不变,两车离乙地的距离y(单位:km)与慢车行驶时间x(单位:h)的函数关系如图,则两车先后两次相遇的间隔时间是( )
A.h B.h C.h D.2h
6.A、B两地相距80km,甲、乙两人沿同一条路从A地到B地.l1,l2分别表示甲、乙两人离开A地的距离s(km)与时间t(h)之间的关系.对于以下说法:①乙车出发1.5小时后甲才出发;②两人相遇时,他们离开A地20km;③甲的速度是40km/h,乙的速度是km/h;④当乙车出发2小时时,两车相距13km.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
7.货车和轿车分别沿同一路线从A地出发去B地,已知货车先出发10分钟后,轿车才出发,当轿车追上货车5分钟后,轿车发生了故障,花了20分钟修好车后,轿车按原来速度的继续前进,在整个行驶过程中,货车和轿车均保持各自的速度匀速前进,两车相距的路程y(米)与货车出发的时间x(分钟)之间的关系的部分图象如图所示,对于以下说法:①货车的速度为1500米/分;②OA∥CD;③点D的坐标为(65,27500);④图中a的值是,其中正确的结论有( )个.
A.1 B.2 C.3 D.4
8.已知A、B两地相距810千米,甲车从A地匀速前往B地,到达B地后停止.甲车出发1小时后,乙车从B地沿同一公路匀速前往A地,到达A地后停止.设甲、乙两车之间的距离为y(千米),甲车出发的时间为x(小时),y与x的关系如图所示,对于以下说法:①乙车的速度为90千米/时;②点F的坐标是(9,540);③图中a的值是13.5;④当甲、乙两车相遇时,两车相遇地距A地的距离为360千米.其中正确的结论是( )
A.①②③ B.①②④ C.②③④ D.①③④
9.甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h,如图是甲、乙两车行驶的距离y(km)与时间x(h)的函数图象,有以下结论:①m=1;②a=40;③甲车从A地到B地共用了6.5小时;④当两车相距50km时,乙车用时为h.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
10.一辆快车和一辆慢车将一批物资从甲地运往乙地,其中快车送达后立即沿原路返回,且往返速度的大小不变,两车离甲地的距离y(单位:km)与慢车行驶时间t(单位:h)的函数关系如图,则两车先后两次相遇的间隔时间是( )
A.h B.h C.h D.h
11.笔直的海岸线上依次有A,B,C三个港口,甲船从A港口出发,沿海岸线匀速驶向C港口,1小时后乙船从B港口出发,沿海岸线匀速驶向A港口,两船同时到达目的地.甲船的速度是乙船的1.25倍,甲、乙两船与B港口的距离y(km)与甲船行驶时间x(h)之间的函数关系如图所示.给出下列说法:①A,B港口相距400km;②乙船的速度为80km/h;③B,C港口相距200km;④乙船出发4h时,两船相距220km.其中正确是 (填序号).
12.小明早8点从家骑自行车出发,沿一条直路去公园锻炼,小明出发的同时,他的爸爸锻炼结束从公园沿同一条道路匀速步行回家;小明在公园锻炼了一会后沿原路以原速返回,小明比爸爸早3分钟到家.设两人离家的距离s(m)与小明离开家的时间t(min)之间的函数关系如图所示,有以下说法:①公园与家的距离为1200米;②爸爸的速度为48m/min;③小明到家的时间为8:22;④小明在返回途中离家360米处与爸爸相遇.其中,说法正确的是: (请把正确说法的序号都填在横线上).
13.“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程).有下列说法:①“龟兔再次赛跑”的路程为1000米;②兔子先到达终点;③乌龟比兔子晚出发40分钟;④兔子在760米处追上乌龟.其中正确的说法是 .(把你认为正确说法的序号都填上)
14.小明和小杰在同一直道的A,B两点间作匀速往返走锻炼(忽略掉头等时间).小明从A地出发,同时小杰从B地出发,两人第一次相遇时小明曾停下接电话数分钟.图中的折线表示从开始到小杰第一次到达A地止,两人之间的距离y(米)与行走时间x(分)的函数关系图象.则图中的b= 米,d= 分.
15.甲、乙两车分别从A、B两地同时出发,沿同一条公路相向而行,相遇时甲、乙所走路程的比为2:3,甲、乙两车离AB中点C的路程y(千米)与甲车出发时间t(时)的关系图象如图所示,则下列说法
①乙车的速度为90千米/时;
②a的值为;
③b的值为150;
④当甲、乙车相距30千米时,甲行走了h或h.
正确的是 .
16.甲、乙两车从A地驶向B地,甲车比乙车早行驶2h,并且在途中休息了0.5h,休息前后速度相同,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.则下列结论正确的是 .
①a的值为40;
②当1.5<x≤7时,甲车行驶路程y与时间x的函数表达式为y=40x﹣20;
③乙车比甲车早1.5h到达B地;
④乙车行驶0.5h或2.5h时,两车恰好相距40km.
17.甲、乙两人相约周末沿同一条路线登山,甲、乙两人距地面的高度y(米)与登山时间x(分钟)之间的函数图象如图所示,根据图象所提供的信息解答下列问题.
(1)甲登山的速度是多少?
(2)乙到达A地后决定提速,提速后乙的速度是甲登山速度的3倍,求乙登山全过程中,登山时距地面的高度y(米)与登山时间x(分钟)之间的函数解析式;
(3)在(2)的条件下,当x为多少时,甲、乙两人距地面的高度差为80米?
18.如图,在平面直角坐标系中,一次函数y=﹣x+b的图象与x轴,y轴分别交于B,C两点,与正比例函数y=x的图象交于点A,点A的横坐标为4.
(1)求A,B,C三点的坐标;
(2)若动点M在线段OA上运动,当三角形OMC的面积是三角形OAC的面积的时,求点M的坐标;
(3)若点P(m,1)在三角形AOB的内部(不包括边界),求m的取值范围.
19.已知A、B两地间有C地,客车由A地驶向C地,货车由B地经过C地去A地(客货车在A、C两地间沿同一条路行驶),两车同时出发,匀速行驶.货车的速度是客车速度的.如图是客车、货车离C站的路程y(km)与行驶时间x(h)的函数关系图象.
(1)求货车的速度并求A、B两地间的路程.
(2)求客车y与x的函数关系式并直接写出货车y与x的函数关系式.
(3)求点P的坐标并说出点P的实际意义.
(4)出发后经过多长时间两车间路程是70km?
20.如图,在平面直角坐标系中,O为坐标原点,已知直线y=﹣x+8与x轴、y轴分别交于B、A两点.直线OD⊥直线AB于点D.现有一点P从点D出发,沿线段DO向点O运动,另一点Q从点O出发,沿线段OA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到O时,两点都停止.设运动时间为t秒.
(1)点A的坐标为 .
(2)设△OPQ的面积为S,问当t为何值时S的值最大?最大值是多少?
(3)是否存在某一时刻t,使得△OPQ为等腰三角形?若存在,直接写出所有满足条件的t的值;若不存在,则说明理由.
21.甲、乙两车分别从B,A两地同时出发,甲车匀速前往A地;乙车匀速前往B地,到达B地立即以另一速度按原路匀速返回到A地;设甲、乙两车距A地的路程为y(千米),乙车行驶的时间为x(时),y与x之间的函数图象如图所示.
(1)求乙车从B地到达A地的速度;
(2)求乙车到达B地时甲车距A地的路程;
(3)求乙车返回前甲、乙两车相距40千米时,乙车行驶的时间.
22.如图,在平面直角坐标系中,直线AB:y=﹣x+3,与x轴,y轴交于点A、B,直线x=﹣1与直线AB交于点D,直线l过点A,与y轴交于点C,点C的纵坐标是﹣.
(1)求直线AC的解析式;
(2)在直线l上是否存在点P,点P在直线x=﹣1的左侧,使得S△ABC=S△PDB,若存在,请求出点P的坐标,若不存在,请说明理由.
(3)在第(2)问的条件下,点Q是线段PD的动点,过点Q做QM∥x轴,交直线AB与点M,在x轴上是否存在点N,使得△QMN为等腰直角三角形,若存在,请直接写出点N的坐标,若不存在,请说明理由.
23.如图,在平面直角坐标系中,O为坐标原点,一次函数y=x+4与x轴,y轴分别交于点B,点A,点C的坐标为C(5,0),点P是射线BO上一动点.
(1)点A的坐标是 ;点B的坐标是 ;
(2)连接AP,若△ABP的面积为10,求点P的坐标;
(3)当点P在射线BO上运动时,若△APC是等腰三角形,请直接写出点P的坐标.
24.在一条笔直的公路旁依次有A、B、C三个村庄,甲、乙两人同时分别从A、B两村出发,甲骑摩托车,乙骑电动车沿公路匀速驶向C村,最终到达C村.设甲、乙两人到C村的距离y1,y2(km)与行驶时间x(h)之间的函数关系如图所示,请回答下列问题.
(1)A,C两村间的距离为 km,a= .
(2)求出图中点P的坐标,并解释该点坐标所表示的实际意义.
(3)乙在行驶过程中,何时距甲20km.
25.某剧院举行新年专场音乐会,成人票每张40元,学生票每张10元,剧院制定了两种优惠方案,且每个团体购票时只能选择其中一种优惠方案,方案1:购买一张成人票赠送一张学生票;方案2:按总价的90%付款.某校有4名老师与x(x≥4)名学生去观赏这次音乐会,设用方案1和方案2付款的总金额分别为y1(元)和y2(元).
(1)分别求出y1、y2与x之间的函数关系式;
(2)当学生人数为20名时,请通过计算说明哪种方案更优惠;
(3)请通过计算说明:当学生人数为多少时,选择两种方案一样优惠?
26.为全面打造“艺美郓城”美育品牌,逐步形成具有郓城特色的美育体系.某校学生展示花鼓表演,在笔直的跑道两端有A、B两地相距240米,甲队从A地跑到B地,乙队从B地跑到A地.已知乙队的速度是甲队的2倍,两队同时出发,乙队到达A地后12分钟甲队到达B地.
(1)求甲队每分钟跑 米;
(2)如图表示的是甲、乙两队离B地的距离S(米)与时间t(分钟)之间的函数图象,请分别求出甲、乙两队的函数关系式,并求出甲、乙两队相遇时t的值;
(3)求甲、乙两队相距30米时t的值.
27.小明家、新华书店、学校在一条笔直的公路旁,某天小明骑车上学,当他骑了一段后,想起要买某本书,于是又返回到刚经过的新华书店,买到书后继续骑车去学校,他本次骑车上学的过程中离家距离与所用的时间的关系如图所示,请根据图象提供的信息回答下列问题:
(1)小明家到学校的距离是 米;小明在书店停留了 分钟;
(2)如果骑车的速度超过了300米/分就超越了安全限度,小明买到书后继续骑车到学校的这段时间的骑车速度在安全限度内吗?请说明理由;
(3)请直接写出小明出发后多长时间离家的距离为900米?
28.A、B两地相距60km,甲、乙两人从两地出发相向而行,甲先出发,图中l1,l2表示两人离A地的距离s(km)与时间t(h)的关系,请结合图象解答下列问题:
(1)表示乙离A地的距离与时间关系的图象是 (填“l1”或“l2”);甲的速度是 km/h,乙的速度是 km/h.
(2)甲出发多长时间两人相遇?
(3)甲出发多长时间后两人恰好相距5km?
参考答案
1.解:①两车的速度之差为80÷(b+2﹣b)=40(km/h),
∴a=100﹣40=60,结论①正确;
②两车第一次相遇所需时间=(h),
∵s的值不确定,
∴b值不确定,结论②不正确;
③两车第二次相遇时间为b+2+=b+(h),
∴c=b+,结论③正确;
④∵b=,s=40,
∴b=1,结论④不正确.
故选:D.
2.解:小明首次到达目的地之前的速度是=80(米/分),
故A不正确;
两地间的距离为:80×35=2800(米),
小李在小明到达目的地时行走的路程为:65×(35﹣5)=65×30=1950(米),
∴2800﹣1950=850(米),
此时,小李距目的地还有850米,
故B不正确;C正确;
D、850﹣65×10=200(米),200÷(47﹣45)=100(米/分),100﹣65=35(米/分),
故D不正确;
故选:C.
3.解:由题意可得:甲步行速度==60(米/分);
故①结论正确;
设乙的速度为:x米/分,
由题意可得:16×60=(16﹣4)x,
解得x=80,
∴乙的速度为80米/分;
∴乙走完全程的时间==30(分),
故②结论错误;
由图可得,乙追上甲的时间为:16﹣4=12(分);
故③结论错误;
乙到达终点时,甲离终点距离是:2400﹣(4+30)×60=360(米),
故④结论错误;
故正确的结论有①共1个.
故选:A.
4.解:由图象可得,
a=4+0.5=4.5,故①正确;
甲的速度是460÷(7+)=60(km/h),故②正确;
设乙刚开始的速度是vkm/h,则后来的速度为(v﹣50)km/h,
4v+(7﹣4.5)×(v﹣50)=460,
解得v=90,故③错误;
设乙出发第一次追上甲用时th,
90t=60(t+),
解得t=,
h=80min,故④正确;
故选:B.
5.解:根据图象可知,慢车的速度为=60(km/h).
对于快车,由于往返速度大小不变,总共行驶时间是(9﹣3)h,
故其速度为=180(km/h).
所以对于慢车,y与t的函数表达式为y=540﹣60x (0≤x≤9)①.
对于快车,设当3≤x≤6时,y与x的函数表达式为y=kx+b,
由题意得:,
解得:,
∴对于快车,当3≤x≤6时,y与x的函数表达式为y=﹣180x+1080②,
对于快车,设当6<x≤9时,y与x的函数表达式为y=kx+b,
由题意得:,
解得:,
∴对于快车,当3≤x≤6时,y与x的函数表达式为y=180x﹣1080③,
联立①②,可解得交点横坐标为x=,
联立①③,可解得交点横坐标为x=,
因此,两车先后两次相遇的间隔时间是﹣=(h),
故选:B.
6.解:由图象可得,
乙车出发1.5小时后甲乙相遇,故①错误;
两人相遇时,他们离开A地20km,故②正确;
甲的速度是(80﹣20)÷(3﹣1.5)=40(km/h),乙的速度是km/h,故③正确;
当乙车出发2小时时,两车相距:20+(2﹣1.5)×40﹣×2=km,故④错误;
故选:B.
7.解:①由图象可知,当x=10时,轿车开始出发;当x=45时,轿车开始发生故障,则x=45﹣5=40(分钟),即货车出发40分钟时,轿车追上了货车,
设货车,轿车的速度分别为m米/分,n米/分,
根据题意,得,
解得,
所以货车的速度为1500米/分,故①正确;
②由题意可知,OA段货车在行驶,轿车停止;CD段货车在行驶,轿车发生故障停止,
则OA与x轴夹角和CD与x轴夹角相等,所以OA∥CD,故②正确;
③轿车故障花了20分钟修好,由题意图象可知,B点时x=45,此时轿车开始分钟故障,D点时轿车刚修好,即此时x=45+20=65,
∴D点纵坐标为:(20﹣)×1500=30000﹣2500=27500,
∴D点坐标为:(65,27500),故③正确;
④在D点时,轿车的速度变为原来的,
即此时轿车的速度为:2000×=1800(米/分),
D点坐标为:(65,27500),到x=a时轿车开始追赶货车直到两车相遇,
∴(a﹣65)×(1800﹣1500)=27500,
解得a=65+=,
即图中a的值是,故④正确.
综上所述,正确的结论①②③④.
故选:D.
8.解:由图象可知,
甲车行驶的速度为(810﹣750)÷1=60(千米/时),
设乙车的速度为x千米/时,根据题意得:
6×60+(6﹣1)x=810,
解得x=90.
即乙车的速度为90千米/时,故①正确;
乙车从B地到达A地的时间为810÷90=9(小时),
∵甲车出发1小时后,乙车从B地沿同一公路匀速前往A地,
∴甲车行驶的时间为9+1=10(小时),
∴甲车10小时行驶的路程为60×10=600(千米),
∴点F的坐标为(10,600),故②错误;
甲车从A地匀速前往B地的时间为810÷60=13.5(小时),
∴a=13.5,故③正确;
当甲、乙两车相遇时,甲车行驶了6小时,
行驶的路程为60×6=360(千米),故④正确,
综上,正确的结论是①③④,
故选:D.
9.解:由题意,得m=1.5﹣0.5=1,故①结论正确;
120÷(3.5﹣0.5)=40(km/h),则a=40,故②结论正确;
设甲车休息之后行驶路程y(km)与时间x(h)的函数关系式为y=kx+b,由题意,得:
,
解得,
∴y=40x﹣20(1.5<x≤7),
当y=260时,260=40x﹣20,
解得:x=7,
∴甲车从A地到B地共用了7小时,故③结论错误;
当1.5<x≤7时,y=40x﹣20.
设乙车行驶的路程y与时间x之间的解析式为y=k'x+b',由题意得:
,
解得,
∴y=80x﹣160.
当40x﹣20﹣50=80x﹣160时,
解得:x=,
当40x﹣20+50=80x﹣160时,
解得:x=,
∴﹣2=,﹣2=,
所以乙车行驶小时或小时,两车恰好相距50km,故④结论错误.
∴正确结论的个数是2个.
故选:B.
10.解:根据图象可知,慢车的速度为.
对于快车,由于往返速度大小不变,总共行驶时间是4 h,
因此单程所花时间为2 h,故其速度为.
所以对于慢车,y与t的函数表达式为①.
对于快车,y与t的函数表达式为y=,
联立①②,可解得交点横坐标为t=3,
联立①③,可解得交点横坐标为t=4.5,
因此,两车先后两次相遇的间隔时间是1.5,
故选:B.
11.解:由题意和图象可知,
A、B港口相距400km,故①正确;
∵甲船4个小时行驶了400km,
∴甲船的速度为:400÷4=100(km/h),
∵甲船的速度是乙船的1.25倍,
∴乙船的速度为:100÷1.25=80(km/h),
故②正确;
∵乙船的速度为80km/h,
∴400÷80=(400+sBC)÷100﹣1,
解得:sBC=200km,
故③正确;
乙出发4h时两船相距的距离是:4×80+(4+1﹣4)×100=420(km),
故④错误.
故答案为:①②③.
12.解:由图象可得,
公园与家的距离为1200米,故①正确;
爸爸的速度为:1200÷(12+10+3)=48(m/min),故②正确;
∵10+12+10=22(min),
∴小明到家的时间为8:22,故③正确;
小明的速度为:1200÷10=120(m/min),
设小明在返回途中离家a米处与爸爸相遇,
=12+,
解得,a=240,
即小明在返回途中离家240米处与爸爸相遇,故④不正确;
故答案为:①②③.
13.解:由函数图象可得,
“龟兔再次赛跑”的路程为1000米,故①说法正确;
兔子先到达终点,故②说法正确;
兔子比乌龟晚出发40分钟,故③说法错误;
当40≤x≤60时,设y1与x的函数关系式为y1=kx+b,
∵点(40,600),(60,1000)在该函数图象上,
∴,
解得,
∴当40≤x≤60时,y1与x的函数关系式为y1=20x﹣200;
当40≤x≤50时,设y2与x的函数关系式为y2=mx+n,
∵点(40,0),(50,1000)在该函数图象上,
∴,
解得,
即当40≤x≤50时,y2与x的函数关系式为y2=100x﹣4000;
令20x﹣200=100x﹣4000,
解得x=47.5,
∴当x=47.5时,此时y1=y2=750,
即兔子在750米处追上乌龟,故④错误;
故答案为:①②.
14.解:由折线可知小杰的速度为:4200÷70=60米/分,
且=60,
解得c=30,
则两人速度和为4200÷30=140米/分,故小明速度为:140﹣60=80米/分,
d点表示小明到达B地开始返向,
4200=30×80+(d﹣40)×80,
得d=62.5,
则a=62.5×60=3750,
b=3750﹣(80﹣60)×7.5=3600.
故答案为:3600,62.5.
15.解:①A、B两地之间的距离为30×2÷(﹣)=300(千米),
∴出发时,甲、乙两车离AB中点C的路程是300÷2=150(千米),即b=150,③正确;
②乙车的速度为(150+30)÷2=90(千米/小时),①正确;
③甲车的速度为(150﹣30)÷2=60(千米/小时),
∴a的值为150÷60=,③正确;
④设出发xh甲、乙车相距30千米,
则(90+60)x=300﹣30或(90+60)x=300+30,
解得:x=或x=,故④错误.
综上所述:正确的结论有①②③.
故答案为:①②③.
16.解:a=120÷(3.5﹣0.5)×1=40,故①正确;
当1.5<x≤7时,设甲车行驶路程y与时间x的函数表达式为y=kx+b,
,得,
即当1.5<x≤7时,甲车行驶路程y与时间x的函数表达式为y=40x﹣20,故②正确;
乙车的速度为:120÷(3.5﹣2)=80(km/h),
乙车从A地到B地用的时间为:260÷80=3.25(h),
乙车比甲车早[3.5+(260﹣120)÷40]﹣(2+3.25)=1.75h到达B地,故③错误;
当乙车行驶0.5h时,两车相距[40+(2+0.5﹣1.5)×40]﹣80×0.5=40(km),
当乙车行驶2.5h时,两车相距80×2.5﹣[40+(2﹣1.5+2.5)×40]=40(km),
故④正确;
故答案为:①②④.
17.解:(1)甲登山的速度为:(300﹣100)÷20=10(米/分),
答:甲登山的速度是10米/分;
(2)V乙=3V甲=30米/分,
t=2+(300﹣30)÷30=11(分钟),
设2到11分钟,乙的函数解析式为y=kx+b,
∵直线经过A(2,30),(11,300),
∴,
解得,
∴当2<x≤11时,y=30x﹣30,
设当0≤x≤2时,乙的函数关系式为y=ax,
∵直线经过A(2,30),
∴30=2a解得a=15,
∴当0≤x≤2时,y=15x,
综上,y=;
(3)设甲的函数解析式为:y=mx+100,将(20,300)代入得:300=20m+100,
∴m=10,
∴y=10x+100.
∴当0≤x≤2时,由(10x+100)﹣15x=80,解得x=4>2矛盾,故此时没有符合题意的解;
当2<x≤11时,由|(10x+100)﹣(30x﹣30)|=80得,
|130﹣20x|=80,
∴x=2.5或x=10.5;
当11<x≤20时,由300﹣(10x+100)=80得x=12,
∴x=2.5或10.5或12.
∴当x为2.5或10.5或12时,甲、乙两人距地面的高度差为80米.
18.解:(1)∵点A在正比例函数y=x的图象上,且点A的横坐标为4.
∴点A(4,2),
∵一次函数y=﹣x+b的图象与正比例函数y=x的图象交于点A,
∴2=﹣4+b,
∴b=6,
∴一次函数解析式为y=﹣x+6,
∵一次函数y=﹣x+6的图象与x轴,y轴分别交于B,C两点,
∴点B(6,0),点C(0,6);
(2)由(1)可知:OC=6,xA=4,
∴S△OAC=×OC×xA=×6×4=12,
∵S△OMC=S△OAC=4,
∴S△OMC=×OC×|xM|=4,
∴|xM|=,
∴xM=±,
当动点M在线段OA上时,x>0,则当x=时,y=×=,
∴此时M点的坐标为(,);
(3)∵点P(m,1)在△AOB的内部(不包括边界),
∴当y=1时,代入正比例函数中得:1=x,
解得:x=2,
当y=1时,代入一次函数中得:1=﹣x+6,
解得:x=5,
∴2<m<5.
故答案为:2<m<5.
19.解:(1)由图象可得,
客车的速度:720÷9=80(km/h),
则货车速度:(km/h).
A与B两地间路程为:60×2+720=840(km),
即货车的速度是60km/h,A、B两地间的路程是840km;
(2)设客车y与x的函数关系式是y=kx+b,
,
解得,
即客车y与x的函数关系式是y=﹣80x+720;
当0≤x≤2时,设货车y与x的函数关系式是y=ax+c,
∵货车的速度为60km/h,60×2=120,
∴该函数过点(0,120),(2,0),
∴,
解得,
即当0≤x≤2时,货车y与x的函数关系式是y=﹣60x+120;
720÷60=12,
当2<x≤14时,设货车y与x的函数关系式是y=mx+n,
∵点(2,0),(14,720)在该函数图象上,
∴,
解得,
即当2<x≤14时,货车y与x的函数关系式是y=60x﹣120;
由上可得,货车y与x的函数关系式是y=;
(3)令﹣80x+720=60x﹣120,
解得x=6,
则x=6时,y=60×6﹣120=360﹣120=240,
∴点P的坐标为(6,240),
点P的实际意义是:两车出发6小时,两车相遇.与C地相距240km;
(4)当两车相遇前相距70千米时,
(﹣80x+720)﹣(60x﹣120)=70,
解得x=5.5,
当两车相遇后相距70千米时,
(60x﹣120)﹣(80x+720)=70,
解得x=6.5,
综上所述,出发后经过5.5小时或6.5小时,两车相距70千米.
20.解:(1)y=﹣x+8与x轴、y轴分别交于B、A两点,
令x=0,则y=8,
∴A(0,8),
故答案为:(0,8);
(2)∵A(0,8),
∴OA=8,
令y=0,则﹣x+8=0,
∴x=6,
∴B(6,0),
∴OB=6,
∴AB=10,
∵OD⊥AB,
∴S△AOB=OA×OB=AB×OD,
∴OD==,
如图,过点P作PH⊥OA于H,
在Rt△AOD中,OA=8,OD=,
根据勾股定理得,AD=,
由运动知,DP=t,OQ=t,
∴OP=OD﹣DP=﹣t,
∴PH=(﹣t)×,
∴t=时,S最大,最大值为;
(3)∵△OPQ为等腰三角形,
∴①当OQ=OP时,
∴t=﹣t,
∴t=,
②当OQ=PQ时,在Rt△AOD中
如图,过点Q作QM⊥OD于M,
∴OM=OP=(﹣t),
在Rt△OMQ中,OM=t,
∴(﹣t)=t,
∴t=,
③当PO=PQ时,如图,
过点P作PH⊥OA于H,
∴OH=OQ=t,
在Rt△POH中,OH=(﹣t),
∴t=(﹣t),
∴t=,
∴△OPQ为等腰三角形时,t的值为秒或秒或秒.
21.解:(1)由图象可得,
乙车从A地到B地的速度为:180÷1.5=120(千米/时),
∴120m=300,
解得m=2.5,
∴乙车从B地到达A地的速度为:300÷(5.5﹣2.5)=300÷3=100(千米/时),
即乙车从B地到达A地的速度是100千米/时;
(2)由图象可得,
甲车的速度为:(300﹣180)÷1.5=120÷1.5=80(千米/时),
则乙车到达B地时甲车距A地的路程是:300﹣2.5×80=300﹣200=100(千米),
即乙车到达B地时甲车距A地的路程是100千米;
(3)乙车返回前甲、乙两车相距40千米时,设乙车行驶的时间为t小时,
甲乙相遇之前:80t+120t+40=300,
解得t=1.3;
甲乙相遇之后:80t+120t﹣40=300,
解得t=1.7;
答:乙车返回前甲、乙两车相距40千米时,乙车行驶的时间是1.3小时或1.7小时.
22.解:(1)在y=﹣x+3中,令x=0得y=3,令y=0得x=3,
∴A(3,0),B(0,3),
∵点C的纵坐标是﹣,
∴C(0,﹣),
设直线AC的解析式为y=kx﹣,把A(3,0)代入得:
0=3k﹣,解得k=,
∴直线AC的解析式为y=x﹣;
(2)在直线l上存在点P,使得S△ABC=S△PDB,
设PB交直线x=﹣1于E,如图:
∵A(3,0),B(0,3),C(0,﹣),
∴S△ABC=BC OA=×(3+)×3=,
在y=﹣x+3中,令x=﹣1得y=4,
∴D(﹣1,4),
设P(m,m﹣),直线PB为y=k'x+3,
则m﹣=k'm+3,解得k'=,
∴直线PB为y=x+3,
令x=﹣1得y=,
∴E(﹣1,),
∴DE=4﹣=,
∵S△ABC=S△PDB,
∴DE |xB﹣xP|=,即××(﹣m)=,
解得m=﹣6,
∴P(﹣6,﹣);
(3)在x轴上存在点N,使得△QMN为等腰直角三角形,
由P(﹣6,﹣),D(﹣1,4)得直线PD解析式为y=x+,
设Q(t,t+),
∵QM∥x轴,M在AB上,
∴在y=﹣x+3中令y=t+,得x=﹣t﹣,
∴M(﹣t﹣,t+),
∴QM=﹣t﹣﹣t=﹣,
①当Q为直角顶点时,如图:
∵QM=QN,
∴﹣=t+,
解得t=﹣,
∴N(﹣,0);
②当M为直角顶点时,如图:
∵QM=MN,
∴﹣=t+,
解得t=﹣,
∴N(,0);
③当N为直角顶点时,过N作NH⊥QM,如图:
∵QM=2NH,
∴﹣=2×(t+),
解得t=﹣,
∴Q(﹣,),
∴QH=NH=,
∴ON=﹣=,
∴N(﹣,0);
综上所述,N的坐标为:(﹣,0)或(,0)或(﹣,0).
23.解:(1)在y=x+4中,令y=0,
得x+4=0,
解得:x=﹣8,
∴B(﹣8,0),
令x=0,得y=4,
∴A(0,4),
故答案为:(0,4),(﹣8,0);
(2)∵S△ABP=BP OA=10,
∴×BP×4=10,
∴BP=5,
∴PO=3,
∵点P是射线BO上一动点,
∴P(﹣3,0);
(3)设P(x,0),
①若AP=AC,
∴x2+42=42+52,
∴x=﹣5,x=5(舍去),
∴P(﹣5,0);
②若AC=PC,
∴(5﹣x)2=42+52,
∴x=5+或x=5﹣,
∴P(5+,0)或P(5﹣,0);
③若AP=PC,
∴x2+42=(x﹣5)2,
∴x=,
∴P(,0).
综合以上可得,点P的坐标为(﹣5,0)或(5+,0)或P(5﹣,0)或(,0).
24.解:(1)A、C两村间的距离120km,
a=120÷[(120﹣90)÷0.5]=2;
故答案为120,2;
(2)设y2=k2x+90,
代入(3,0),得0=3k2+90,
解得k2=﹣30,
所以y2=﹣30x+90.
当y1=y2时,
﹣60t+120=﹣30t+90,
解得:t=1,
所以甲乙二人行驶1小时后两人相遇,
此时距离C村60km,
故P点坐标为P(1,60).
(3)当y1﹣y2=20,
即﹣60x+120﹣(﹣30x+90)=20
解得x=,
当y2﹣y1=20,
即﹣30x+90﹣(﹣60x+120)=20
解得x=,
当甲走到C地,而乙距离C地20km时,
﹣30x+90=20
解得x=;
综上所知当x=h,或x=h,或x=h乙距甲20km.
25.解:(1)由题意可得,
y1=4×40+10(x﹣4)=10x+120,
y2=(4×40+10x)×90%=9x+144;
(2)当x=20时,y1=10×20+120=320,
y2=9×20+144=324;
∵320元<324元,
∴当x=20时,方案一更优惠;
(3)令10x+120=9x+144,得x=24,
答:当学生为24人时,两种方案一样优惠.
26.解:(1)由图象可得,
甲队每分钟跑:240÷24=10(米),
故答案为:10;
(2)设甲队离B地的距离S(米)与时间t(分钟)之间的函数关系式为S=kt+b,
∵点(0,240),(24,0)在该函数图象上,
∴,
解得,
即甲队离B地的距离S(米)与时间t(分钟)之间的函数关系式为S=﹣10t+240(0≤t≤24);
设乙队离B地的距离S(米)与时间t(分钟)之间的函数关系式为S=at,
∵点(12,240)在该函数图象上,
∴240=12a,
解得a=20,
即乙队离B地的距离S(米)与时间t(分钟)之间的函数关系式为S=20t(0≤t≤12);
当甲和乙相遇时,﹣10t+240=20t,
解得t=8,
即甲、乙两队相遇时t的值是8;
(3)当甲和乙相遇前相距30米,
﹣10t+240﹣20t=30,
解得t=7;
当甲和乙相遇后相距30米,
∴20t﹣(﹣10t+240)=30,
解得t=9,
即甲、乙两队相距30米时t的值是7或9.
27.解:(1)根据图象,学校的纵坐标为1500,小明家的纵坐标为0,
故小明家到学校的路程是1500米;
根据题意,小明在书店停留的时间为从8分到12分,
故小明在书店停留了4分钟.
故答案为:1500;4;
(2)由图象可知:
12~14分钟时,平均速度==450米/分,
∵450>300,
∴小明买到书后继续骑车到学校,这段时间速度不在安全限度内;
(3)从图象上看,小明出发后离家距离为900米时,一共有三个时间,
①在0~6分钟时,平均速度为:=200米/分,
距家900米的时间为:t1=900÷200=4.5(分);
②在6~8分钟内,平均速度==300米/分,
距家900米时时间为t2,则:1200﹣300(t2﹣6)=900,
解得:t2=7,
③在12~14分钟内,平均速度450米/分,
距家900米时时间为t3,则600+450(t3﹣12)=900,
解得:t3=12,
综上,小明出发4.5分钟或7分钟或12分钟时距家900米.
28.解:(1)∵甲先出发,由图象可知l1,l2分别表示甲、乙的函数图象,
∴甲的速度为60÷2=30(km/h),乙的速度为60÷(3.5﹣0.5)=20(km/h),
故答案为l2,30,20;
(2)设甲出发xh后两人相遇,根据题意得:
30x+20(x﹣0.5)=60,
解得x=1.4,
∴甲出发1.4h后两人相遇;
(3)设甲出发th时后两人恰好相距5km,
①两人相遇前:
30t+20(t﹣0.5)+5=60,
解得t=1.3,
②两人相遇后:
30t+20(t﹣0.5)﹣5=60,
解得:t=1.5,
∴甲出发1.3h或1.5h时后两人恰好相距5km.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
