2021-2022学年沪科版数学九年级下册24.6正多边形和圆的练习题 (Word版含答案)
文档属性
| 名称 | 2021-2022学年沪科版数学九年级下册24.6正多边形和圆的练习题 (Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 152.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-30 00:00:00 | ||
图片预览


文档简介
正多边形和圆的练习题
半径为的圆内接正三角形、正方形、正六边形的边心距分别为,,,则,,的大小关系是
A. B. C. D.
如图,等边三角形和正方形都内接于,则:
: B. : C. : D. :
已知正六边形的边长为,则它的内切圆的半径为
B. C. D.
如图,正方形内接于,线段在对角线上运动,若的面积为,,则周长的最小值是
B. C. D.
如图,、、、为一个正多边形的顶点,为正多边形的中心,若,则这个正多边形的边数为______.
如图,五边形是的内接正五边形,是的直径,则的度数是______
如图,在正六边形中,连接对角线,,,,,与交于点,与交于点为,与交于点,分别延长,于点,设有以下结论:
的重心、内心及外心均是点
四边形绕点逆时针旋转与四边形重合
则所有正确结论的序号是______ .
如图,外接于正方形,为弧上一点,且,,求正方形的边长和的长.
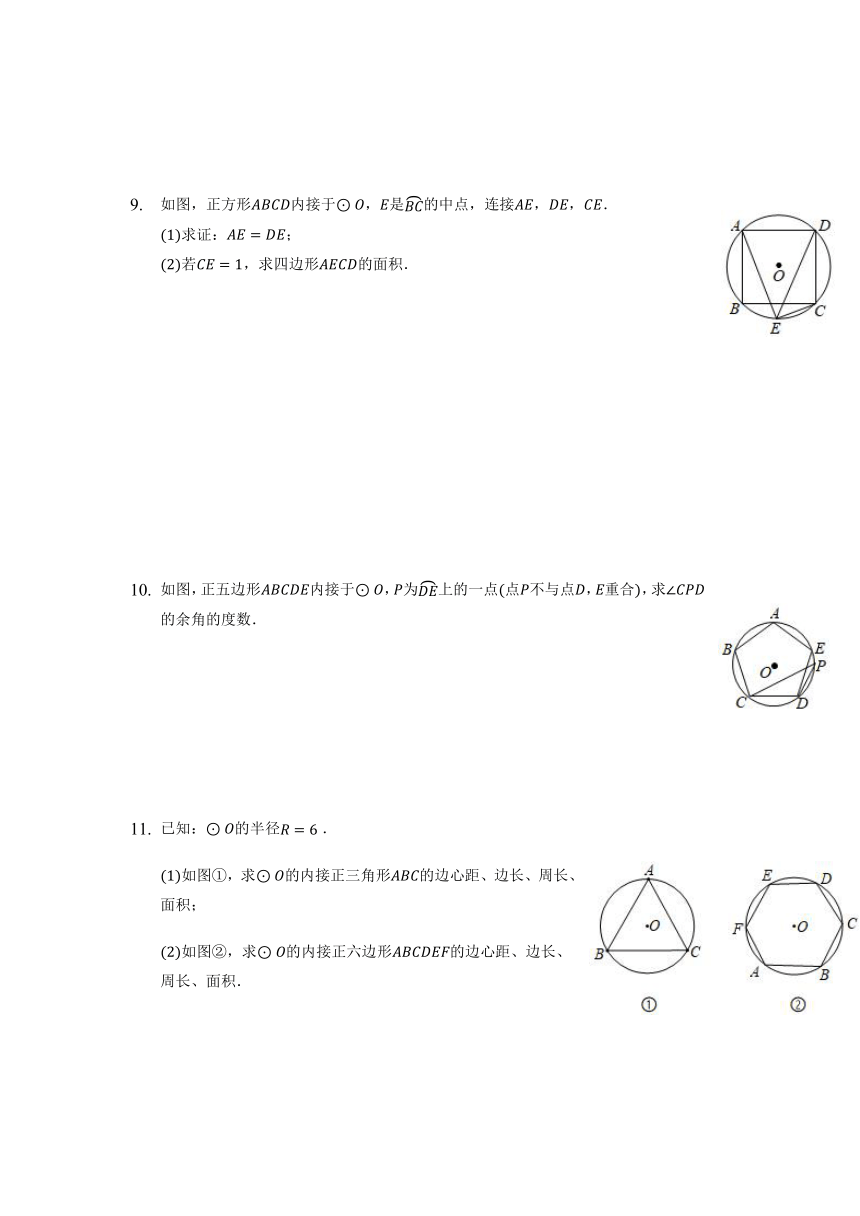
如图,正方形内接于,是的中点,连接,,.
求证:;
若,求四边形的面积.
如图,正五边形内接于,为上的一点点不与点,重合,求的余角的度数.
已知:的半径.
如图,求的内接正三角形的边心距、边长、周长、面积;
如图,求的内接正六边形的边心距、边长、周长、面积.
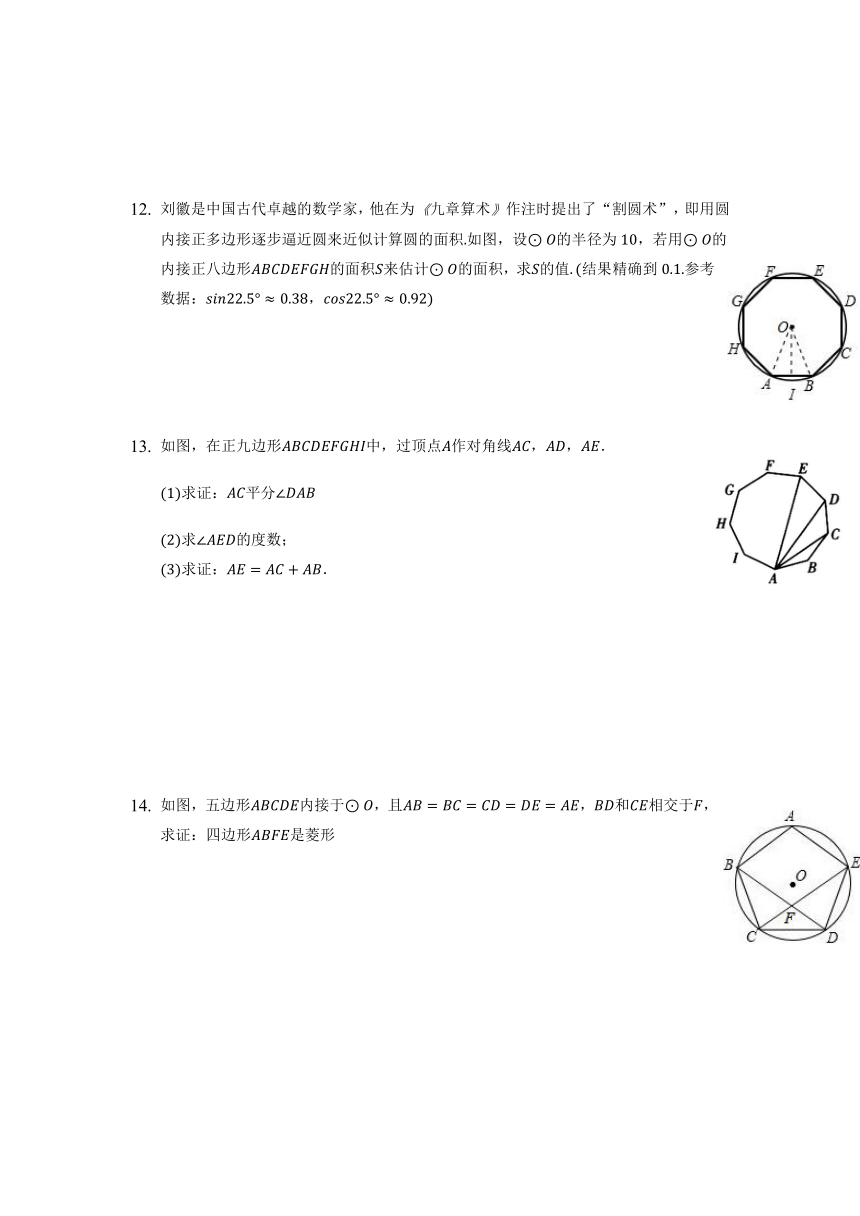
刘徽是中国古代卓越的数学家,他在为九章算术作注时提出了“割圆术”,即用圆内接正多边形逐步逼近圆来近似计算圆的面积如图,设的半径为,若用的内接正八边形的面积来估计的面积,求的值结果精确到参考数据:,
如图,在正九边形中,过顶点作对角线,,.
求证:平分
求的度数;
求证:.
如图,五边形内接于,且,和相交于,求证:四边形是菱形
答案
1.【答案】
解:设圆的半径为,
则正三角形的边心距为
正方形的边心距为,
正六边形的边心距为
,
,
故选:.
2.【答案】
解:连接、、,过作于,如图所示:
则,
正方形和等边三角形都内接于,
,,
,
是等腰直角三角形,,
,,
,
,
,
,
故选:.
3.【答案】
解:正六边形一条边的两个端点与其内切圆圆心的连线及这条边构成一个等边三角形,
正六边形的内切圆半径即为这个等边三角形的高,
所以内切圆半径,
故选B
4.【答案】
【解析】解:的面积为,则圆的半径为,则,
由正方形的性质,知点是点关于的对称点,
过点作,且使,
连接交于点,取,连接、,则点、为所求点,
理由:,且,则四边形为平行四边形,
则,
故的周长为最小,
则,
则的周长的最小值为,
故选:.
5.【答案】
【解析】解:连接,,
、、、为一个正多边形的顶点,为正多边形的中心,
点、、、在以点为圆心,为半径的同一个圆上,
,
,
这个正多边形的边数,
故答案为:.
6.【答案】
解:连接,
是的直径,
,
五边形是的内接正五边形,
,
,
,
,
,
,
,
,
故答案为:.
7.【答案】
【解析】解:如图,连接.
在和中,
,
≌,
,
同法可证,,
,
四边形是菱形,故正确,
,,
,
,
是等边三角形,
,故正确,
,
是等边三角形,
,,
点是的重心、内心及外心,故正确,
,
四边形绕点逆时针旋转与四边形重合,故错误,
故答案为:.
正确.证明四边形是菱形即可.
正确.证明是等边三角形,求出即可.
正确.证明是等边三角形即可.
错误.应该是四边形绕点逆时针旋转与四边形重合.
8.【答案】解:连接,作于,如图所示:
四边形是正方形,
,,,
是的直径,是等腰直角三角形,
,,
,
,
,,
是等腰直角三角形,
,
,
.
9.【答案】证明:四边形是正方形,
,
,
是的中点,
,
,
.
解:连接,过点作交的延长线于.
四边形是正方形,
,,
,
,
,
,
,
在和中,
,
≌,
,
,
,
,,
,
,
.
10.【答案】解:如图,连接,.
五边形是正五边形,
,
,
的余角的度数为.
11.【答案】解:如图,连接,过点作于点.
由题意,得,,
,
边心距,
.
由垂径定理得边长,
周长,面积.
如图,连接,过点作于点.
由题意,得,.
,
边心距.
由垂径定理得边长,
周长,面积
12.【答案】解:如图,连接,,则,.
过点作于点,则,
,,
.
13.【答案】证明:多边形是正九边形,
正九边形中各点共圆,
,
在同圆中相等的弦所对的圆周角相等,
平分;
解:正九边形的每个外角为,
每个内角为,
,
,
,
,
;
证明:如图,连接交于点,
由推知,
为等边三角形,
,,,
≌,
,
又,
.
14.【答案】证明:五边形内接于圆,且,
五边形是正五边形,
,
,
,
,
,
,同理 ,
四边形是平行四边形,
,
四边形是菱形.
半径为的圆内接正三角形、正方形、正六边形的边心距分别为,,,则,,的大小关系是
A. B. C. D.
如图,等边三角形和正方形都内接于,则:
: B. : C. : D. :
已知正六边形的边长为,则它的内切圆的半径为
B. C. D.
如图,正方形内接于,线段在对角线上运动,若的面积为,,则周长的最小值是
B. C. D.
如图,、、、为一个正多边形的顶点,为正多边形的中心,若,则这个正多边形的边数为______.
如图,五边形是的内接正五边形,是的直径,则的度数是______
如图,在正六边形中,连接对角线,,,,,与交于点,与交于点为,与交于点,分别延长,于点,设有以下结论:
的重心、内心及外心均是点
四边形绕点逆时针旋转与四边形重合
则所有正确结论的序号是______ .
如图,外接于正方形,为弧上一点,且,,求正方形的边长和的长.
如图,正方形内接于,是的中点,连接,,.
求证:;
若,求四边形的面积.
如图,正五边形内接于,为上的一点点不与点,重合,求的余角的度数.
已知:的半径.
如图,求的内接正三角形的边心距、边长、周长、面积;
如图,求的内接正六边形的边心距、边长、周长、面积.
刘徽是中国古代卓越的数学家,他在为九章算术作注时提出了“割圆术”,即用圆内接正多边形逐步逼近圆来近似计算圆的面积如图,设的半径为,若用的内接正八边形的面积来估计的面积,求的值结果精确到参考数据:,
如图,在正九边形中,过顶点作对角线,,.
求证:平分
求的度数;
求证:.
如图,五边形内接于,且,和相交于,求证:四边形是菱形
答案
1.【答案】
解:设圆的半径为,
则正三角形的边心距为
正方形的边心距为,
正六边形的边心距为
,
,
故选:.
2.【答案】
解:连接、、,过作于,如图所示:
则,
正方形和等边三角形都内接于,
,,
,
是等腰直角三角形,,
,,
,
,
,
,
故选:.
3.【答案】
解:正六边形一条边的两个端点与其内切圆圆心的连线及这条边构成一个等边三角形,
正六边形的内切圆半径即为这个等边三角形的高,
所以内切圆半径,
故选B
4.【答案】
【解析】解:的面积为,则圆的半径为,则,
由正方形的性质,知点是点关于的对称点,
过点作,且使,
连接交于点,取,连接、,则点、为所求点,
理由:,且,则四边形为平行四边形,
则,
故的周长为最小,
则,
则的周长的最小值为,
故选:.
5.【答案】
【解析】解:连接,,
、、、为一个正多边形的顶点,为正多边形的中心,
点、、、在以点为圆心,为半径的同一个圆上,
,
,
这个正多边形的边数,
故答案为:.
6.【答案】
解:连接,
是的直径,
,
五边形是的内接正五边形,
,
,
,
,
,
,
,
,
故答案为:.
7.【答案】
【解析】解:如图,连接.
在和中,
,
≌,
,
同法可证,,
,
四边形是菱形,故正确,
,,
,
,
是等边三角形,
,故正确,
,
是等边三角形,
,,
点是的重心、内心及外心,故正确,
,
四边形绕点逆时针旋转与四边形重合,故错误,
故答案为:.
正确.证明四边形是菱形即可.
正确.证明是等边三角形,求出即可.
正确.证明是等边三角形即可.
错误.应该是四边形绕点逆时针旋转与四边形重合.
8.【答案】解:连接,作于,如图所示:
四边形是正方形,
,,,
是的直径,是等腰直角三角形,
,,
,
,
,,
是等腰直角三角形,
,
,
.
9.【答案】证明:四边形是正方形,
,
,
是的中点,
,
,
.
解:连接,过点作交的延长线于.
四边形是正方形,
,,
,
,
,
,
,
在和中,
,
≌,
,
,
,
,,
,
,
.
10.【答案】解:如图,连接,.
五边形是正五边形,
,
,
的余角的度数为.
11.【答案】解:如图,连接,过点作于点.
由题意,得,,
,
边心距,
.
由垂径定理得边长,
周长,面积.
如图,连接,过点作于点.
由题意,得,.
,
边心距.
由垂径定理得边长,
周长,面积
12.【答案】解:如图,连接,,则,.
过点作于点,则,
,,
.
13.【答案】证明:多边形是正九边形,
正九边形中各点共圆,
,
在同圆中相等的弦所对的圆周角相等,
平分;
解:正九边形的每个外角为,
每个内角为,
,
,
,
,
;
证明:如图,连接交于点,
由推知,
为等边三角形,
,,,
≌,
,
又,
.
14.【答案】证明:五边形内接于圆,且,
五边形是正五边形,
,
,
,
,
,
,同理 ,
四边形是平行四边形,
,
四边形是菱形.
