2021-2022学年沪科版 八年级上册数学第15章 轴对称图形和等腰三角形 单元测试卷(word解析版)
文档属性
| 名称 | 2021-2022学年沪科版 八年级上册数学第15章 轴对称图形和等腰三角形 单元测试卷(word解析版) |

|
|
| 格式 | docx | ||
| 文件大小 | 196.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-31 00:00:00 | ||
图片预览



文档简介
第15章 轴对称图形和等腰三角形 单元测试卷1(沪科版 八年级上册)
考试时间:120分钟 满分:150分
姓名:__________ 班级:__________ 考号:__________ 得分:__________
一、单选题(共10题;共40分)
1.在平面直角坐标系中,点B的坐标是(4,-1),点A与点B关于x轴对称,则点A的坐标是( )
A. (4,1) B. (-1,4) C. (-4,-1) D. (-1,-4)
2.观察下列四个图案,可以发现它们具有一个共有的性质,
那么下面四个三位数形成的图案中,具有上述类似共有性质的一个三位数是( )
A. 228 B. 303 C. 808 D. 609
3.等腰三角形的一个角为40°,那么底角等于( )
A. 40° B. 100° C. 70 D. 40°或70°
4.如图所示,△ ABC中,AC=AD=BD , ∠DAC=80°,则∠B的度数为( )
A. 40° B. 35° C. 25° D. 20°
5.如图,已知等边 分别在 上,且 ,连接 交 点.则
A. 30° B. 45° C. 60° D. 80°
6.如图,∠C=90°,AD平分∠BAC交BC于D , 若BC=5 cm , BD=3 cm , 则点D到AB的距离为( )cm .
A. 3 B. 4 C. 2 D. 1
7.如图,△ ABC中,AB=AC,AD=DE, ∠BAD=18°,∠EDC=12°,则 ∠DAE的度数是 ( )
A. 52° B. 58° C. 60° D. 62°
8.如图,已知 ,以 两点为圆心,大于 的长为半径画圆弧,两弧相交于点 ,连接 与 相交于点 ,则 的周长为( )
A. 8 B. 9 C. 11 D. 13
9.如图,在等边△ ABC中,点E是AC边的中点,点P是△ ABC的中线AD上的动点,且AD=6,则PE+PC的最小值是 ( )
A. 12 B. 9 C. 6 D. 3
10.如图,在平面直角坐标系中,等腰直角三角形 OA1A2 的直角边 OA1 在 y轴的正半轴上,且 OA1=A1A2=1,以 OA2 为直角边作第二个等腰直角三角形 OA A3, 以 OA3为直角边作第三个等腰直角三角形OA3A4, …,依此规律,得到等腰直角三角形 OA2021A2022, 则点 A2021 的坐标为( )
A. (0,-21010) B. (-21010 , 0) C. (0,-21009) D. (-21009 , 0)
二、填空题(共4题;共20分)
11. AD,AE分别是等边三角形ABC的高和中线,则AD 与AE 的大小关系为 ________.
12. 如图,AD是等边三角形ABC的中线,AE=AD,则∠EDC= ________.
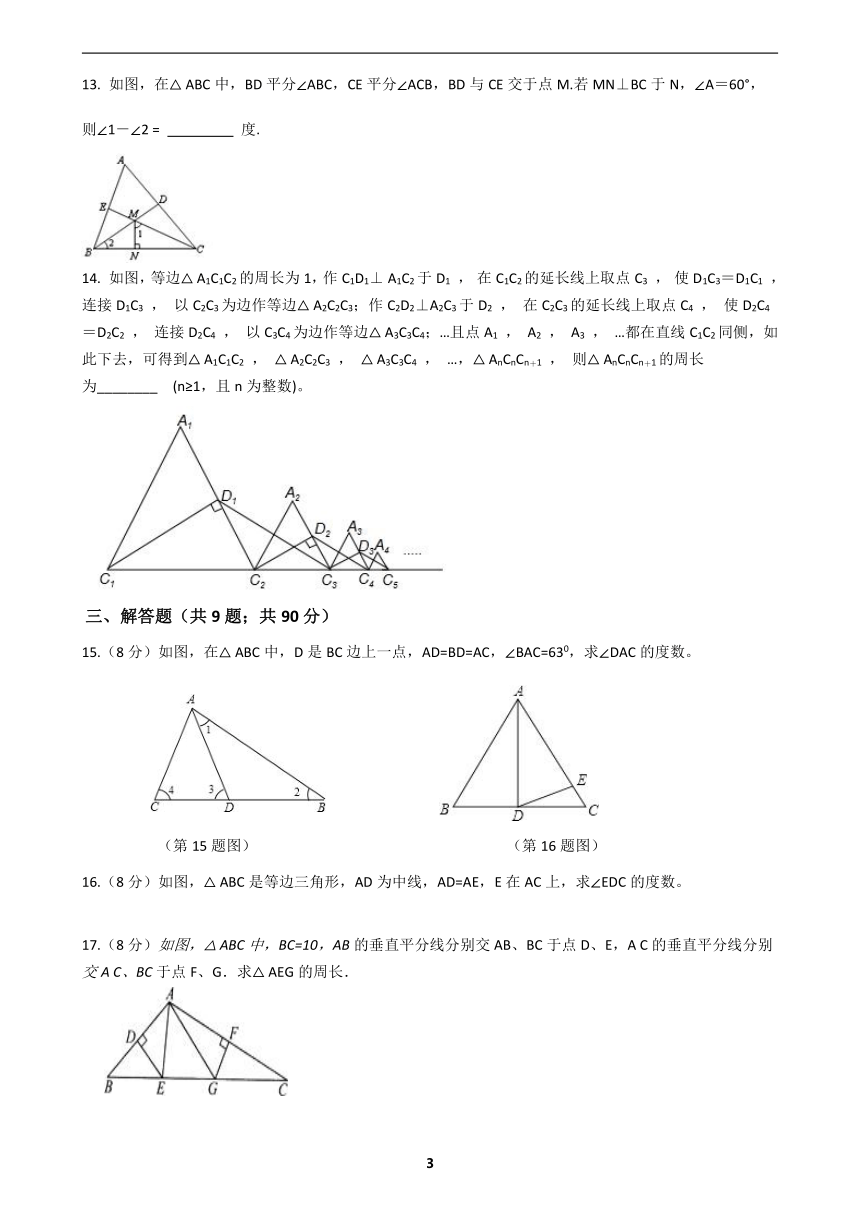
13. 如图,在△ ABC中,BD平分∠ABC,CE平分∠ACB,BD与CE交于点M.若MN⊥BC于N,∠A=60°,
则∠1-∠2 = 度.
14. 如图,等边△ A1C1C2的周长为1,作C1D1⊥ A1C2于D1 , 在C1C2的延长线上取点C3 , 使D1C3=D1C1 , 连接D1C3 , 以C2C3为边作等边△ A2C2C3;作C2D2⊥A2C3于D2 , 在C2C3的延长线上取点C4 , 使D2C4=D2C2 , 连接D2C4 , 以C3C4为边作等边△ A3C3C4;…且点A1 , A2 , A3 , …都在直线C1C2同侧,如此下去,可得到△ A1C1C2 , △ A2C2C3 , △ A3C3C4 , …,△ AnCnCn+1 , 则△ AnCnCn+1的周长
为________ (n≥1,且n为整数)。
三、解答题(共9题;共90分)
15.(8分)如图,在△ ABC中,D是BC边上一点,AD=BD=AC,∠BAC=630,求∠DAC的度数。
(第15题图) (第16题图)
16.(8分)如图,△ ABC是等边三角形,AD为中线,AD=AE,E在AC上,求∠EDC的度数。
17.(8分)如图,△ ABC中,BC=10,AB的垂直平分线分别交AB、BC于点D、E,A C的垂直平分线分别交A C、BC于点F、G.求△ AEG的周长.
18.(8分)如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
①请画出△ ABC关于y轴对称的△ A1B1C1;
②请画出△ ABC关于原点对称的△ A2B2C2;
③在x轴上求作一点P,使△ PAB的周长最小,请画出△ PAB,并直接写出点P的坐标。
19.(10分)如图,AC平分∠BAD,CE⊥ AB于E,CF⊥AD于F,且BC=DC。求证:BE=DF。
(第19题图) (第20题图)
20.(10分)如图,在△ ABC中,AB=AC,点E是AC上一点,ED⊥BC于点D,DE的延长线交BA的延长线于点F.求证:△ AEF是等腰三角形.
21.(12分)如图,已知AD为△ ABC的高,∠B = 2∠C,求证:CD = AB + BD .
(第21题图) (第22题图)
22.(12分)如图,点F是长方形ABCD的BC彼岸上一点,把这张长方形纸片ABCD沿直线AF折叠,已知∠ADB=20°,那么∠BAF应为多少度时,才能使AB′∥ BD ?
23.(14分)如图,△ABC中,AD⊥ BC于D,BD=AC+CD,若∠ BAC=100°,求∠ ACD的度数。
2021-2022学年度 初中数学 月考卷 答题卡
学校:___________姓名:___________班级:___________考号:___________
一、单选题(40分,每题5分)
1 2 3 4 5 6 7 8 9 10
二、填空题(20分,每题5分)
11题、
12题、
13题、
14题、
三、解答题(90分)
15题(8分)
16题(8分)
17题(8分)
18题(8分)
19题(10分)
20题(10分)
21题(12分)
22题(12分)
23题、
第15章 轴对称图形和等腰三角形 单元测试卷1(沪科版 八年级上册)
答案解析部分
一、单选题: ACDCC CDACA
1.【答案】 A
【解析】【解答】解:∵ 点B的坐标是(4,﹣1),点A与点B关于x轴对称,
∴ 点A的坐标是:(4,1).故答案为:A.
【分析】根据轴对称
2.【答案】 C
【解析】【解答】解:四个图形都是轴对称图形,只有三位数808组成的图案是轴对称图形.
故C符合题意. 故答案为:C.
【分析】根据轴对称图形的定义判断.如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形.
3.【答案】 D
【解析】【解答】首先要讨论40°的角是顶角还是底角,再利用等腰三角形的性质和三角形内角和定理求出底角.当等腰三角形的顶角为40°时,则底角等于70°;当等腰三角形的底角为40°时,则底角等于40°.故选D.
【分析】学会运用分类讨论的思想解决问题.熟练掌握等腰三角形的性质和三角形的内角和定理.
4.【答案】 C
【解析】【解答】解:∵ AC=AD , ∠DAC=80°, ∴ ∠ADC=∠C=50°,
∵ AD=BD , ∠ADC=∠B+∠BAD=50°,∴ ∠B=25°,故答案为:C.
【分析】先根据等腰三角形的性质及三角形的内角和定理求出∠ADC的度数,再根据等腰三角形的性质及三角形外角与内角的关系求出∠B的度数即可。
5.【答案】C ∵ 是等边三角形 ∴ ,
易知 ,∴
∴ .
【解析】【分析】利用SAS得出 , 是关键。
6.【答案】 C
【解析】【解答】解:作DE⊥ AB于E , 如下图,
∴ DE=CD=CD=2cm , 即点D到AB的距离为2cm , 故答案为:C .
【分析】过点D作DE⊥AB于E , 通过角平分线的性质进行求解即可得到点D到AB的距离.
7.【答案】 D
【解析】【解答】设∠ADE=x°,且∠BAD=18°,∠EDC=12°,
∴ ∠B+18°=x°+12°,∴ ∠B=x°-6°,
∵ AB=AC,∴ ∠C=∠B=x°-6°,∴ ∠DEA=∠C+∠EDC=x°-6°+12°=x°+6°,
∵ AD=DE,∴ ∠DEA=∠DAE=x°+6°,
在△ ADE中,由三角形内角和定理可得,x+x+6+x+6=180,解得x=56,即∠ADE=56°,∴ ∠DAE=62°
故答案为:D.
【分析】设∠ADE=x°,且∠BAD=18°,∠EDC=12°,根据三角形的外角可得∠B+18°=x°+12°,化简为∠B=x°-6°,再利用等边对等角的性质可得∠C=∠B=x°-6°,∠DEA=∠DAE=x°+6°,最后利用三角形的内角和
8.【答案】 A
【解析】【解答】解:由作法得 垂直平分 (线段垂直平分线的定义),
的周长 ,
故答案为:A.
【分析】利用线段垂直平分线的性质可证得DA=DB,再证明△ BDC的周长=AC+BC,然后代入计算.
9.【答案】 C 【解析】【解答】解:
连BP,则由△PBD与△ PCD 全等,可得 PC=PB,于是 PE+PC=PE+PB
两点直角选段最短,故当B、P、E共线时,PE+PC 最短,为 BE的长,而在同一等边三角形中,
三边上的高相等,故 BE=AD=6, 故答案为:C.
【分析】根据题意,求PE+PC的最小值,将其转化为PE+PCP的值是关键。
10.【答案】 A
【解析】【解答】解:∵ 等腰直角三角形 的直角边 在y轴的正半轴上,且 ,以 为直角边作第二个等腰直角三角形 ,以 为直角边作等腰直角三角形 …
∴ , , ,…, ,
∵ 、 、 …每8个一循环,再回到y轴的正半轴,
,
∴ 点 在y轴的负半轴上,
∵ ,
∴ .
故答案为:A.
【分析】先根据等腰直角三角形的性质发现 , , ,…, 的规律,再根据8个点一循环,确定 的位置,得到它的点坐标.
二、填空题
11.【答案】 相等
【解析】【解答】根据等边三角形三线合一的性质,可以求得等边三角形每个内角的角平分线和其对应边的中线、高线重合,所以AD 与AE相等
【分析】根据等腰三角形三线合一和等边三角形是特殊的等腰三角形可求解.
12.【答案】 15°
【解析】【解答】解:∵ AD是等边△ ABC的中线,
∴ AD⊥BC,∠BAD=∠CAD= ∠BAC= ×60°=30°,∴ ∠ADC=90°,
∵ AD=AE,∴ ∠ADE=∠AED= =75°,∴ ∠EDC=∠ADC-∠ADE=90°-75°=15°.
故答案为:15°.
【分析】根据等边三角形的性质得出AD⊥BC,∠CAD= 30°,进而根据等边对等角及三角形的内角和定理即可算出∠ADE的度数,最后根据∠EDC=∠ADC-∠ADE即可算出答案.
13.【答案】 30
【解析】【解答】解:∵ ∠BMC=180°- (∠ABC+∠ACB)=180°- (180°-∠A)=90°+ ∠A=120°,
∴ ∠1+∠BMN=120°①,
∵ MN⊥BC,∴ ∠2+∠BMN=90°②,
①-②得:∠1-∠2=30°.故答案为:30.
【分析】根据外角平分线的性质,可通过角的运算得出∠1-∠2的度数。
14.【答案】
【解析】【解答】解: 等边三角形 的周长为1,作 于点 ,
,,
,
的周长= 的周长= ,
的周长分别为
故答案为:
【分析】利用等边三角形的性质和特殊角去解题.
三、解答题
15.【答案】 ∵ AD=BD=CA,
由图可知,∠3=∠1+∠2,∠3=∠4,∠1=∠2,∠BAC=63°,∴ ∠4=∠1+∠2=2∠2,
∵ ∠BAC+∠2+∠4=180°,即3∠2+63°=180°,∴ ∠2=39°,∠DAC=∠BAC-∠1=63°-39°=24°.
【解析】【分析】 由等腰三角形的性质及三角形外角的性质可得∠3=∠1+∠2,∠3=∠4,∠1=∠2,在△ ACD中,利用三角形的内角和可得∠BAC+∠2+∠4=180°, 据此求出∠2的度数,即得∠1的度数,根据∠DAC=∠BAC-∠1即可求解.
16.【答案】 解:∵ △ ABC是等边三角形,AD为中线, ∴ AD⊥BC,∠CAD=30°,
∵ AD=AE,∴ ∠ADE=∠AED= = =75°,∴ ∠EDC=∠ADC﹣∠ADE=90°﹣75°=15°.
【解析】【分析】先根据△ ABC是等边三角形,AD为中线可得出AD⊥BC,∠CAD=30°,再由AD=AE可知∠ADE=∠AED,根据三角形内角和定理即可求出∠ADE的度数,故可得出∠EDC的度数.
17.【答案】 解:∵ DE垂直平分AB.∴ AE=BE.同理AG=CG.∴ △ AEG的周长=AE+AG+GE=BE+CG+GE=BC=10.
【解析】【分析】由于DE为AB的中垂线,则AE=BE,又由于FG是AC的中垂线,则AG=GC,△ AEG的周长等于AE+EG+GA也就是等于BE+EG+GC=BC从而可求出△ AEG的周长
18.【答案】 解:△ A1B1C1、△ A2B2C2、△ PAB如图所示,P(2,0)
【解析】【分析】(1)根据关于y轴对称的点的坐标的变化规律:横坐标变为原来的相反数,纵坐标不变,求出A、B、C的对应点的坐标,再在平面直角坐标系中画出图形即可;
(2)根据关于原点对称的点的坐标的变化规律:横坐标与纵坐标都变为原来的相反数,求出A、B、C的对应点的坐标,再在平面直角坐标系中画出图形即可;
(3)找出点A关于x轴的对称点,再将B连接起来与x轴的交点即为点P。
19.【答案】 解:∵ AC平分∠BAD,∴ ∠1=∠2
∵ CE⊥AB于E,CF⊥AD于F,∴ CE=CF
∵ 在Rt△ DCF与Rt△ ECB中,CE=CF, BC=DC,∴ Rt△ DCF≌Rt△ ECB(HL),∴ BE=DF
【解析】【分析】根据角平分线的性质得出CE=CF,然后根据HL证得Rt△ DCF与Rt△ ECB全等,即可证明BE=DF。
20.【答案】 解:DF⊥BC,∴ ∠B+∠F=90°,∠C+∠DEC=90°,∵ AB= AC,∴ ∠B=∠C,∴ ∠F=∠DEC,∵ ∠AEF =∠DEC,∴ ∠F=∠AEF,∴ AE = AF, ∴ AEF是等腰三角形.
【解析】【分析】根据题意,由三角形的内角和定理以及等量代换,证明三角形为等腰三角形即可。
21.【答案】 证明:在DC取点E,使DE=BD,连接AE,
∵ AD为△ ABC的高,∴ AD⊥BE,∴ AB=AE,∴ ∠AEB=∠B,
又∵ ∠B=2∠C,∴ ∠AEB=2∠C,
∵ ∠AEB=∠C+∠EAC,∴ ∠C=∠EAC,∴ AE=EC=AB,
∵ CD=DE+EC,BD=DE,∴ CD=AB+BD.
【解析】【分析】在DC取点E,使DE=BD,连接AE,根据线段垂直平分线求出AB=AE,推出∠B=∠AEB=2∠C=∠C+∠EAC,推出∠C=∠EAC,推出AE=EC=AB,代入即可求出答案.
22.【答案】 ∠BAF应为55度
理由是:∵ ∠ADB = 20°,四边形ABCD是长方形,∴ ∠ABD =70°.
∵ 要 使AB′∥ BD,需使∠BAB′= 110°,由折叠可知∠BAF = ∠B′AF,∴ ∠BAF应为55度
【解析】【分析】先根据直角三角形的性质求出∠ABD的度数,再由平行线的性质求出∠BAB′的度数,根据图形翻折变换的性质即可得出结论.
23.【答案】 解:如图,以A为圆心,AC长为半径画弧,交BC于点E,连接AE,
则AE=AC,CD=DE,∠ CAD=∠ EAD,又BD=AC+DC,BD=BE+DE,
∴ AE=AC=BE,∴ ∠ B=∠ BAE
设∠ ACD=x,则∠ CAD=90°-x,∠ B=∠ BAE=100°-2(90°-x)=100°-180°+2x=2x-80°,
故 ∠AED=2∠B=4x-160°,
在三角形AEC中,由三角形内角和定理得:x+2(90°-x)+(4x-160°)=180°,解得:x= .
【解析】【分析】 以A为圆心,AC长为半径画弧,交BC于点E,连接AE,由等腰三角形的性质可得 CD=DE , ∠CAD=∠EAD , 进而得出 AE=AC=BE ,根据等边对等角得出 ∠B=∠BAE ,并设∠C=x,然后用含x的式子表示出∠CAD及∠B与∠BAE,最后根据三角形的内角和定理列出方程,解方程可以得到∠C的度数.
【解法二】在DC延长线上,截取一段CF=CA。7
考试时间:120分钟 满分:150分
姓名:__________ 班级:__________ 考号:__________ 得分:__________
一、单选题(共10题;共40分)
1.在平面直角坐标系中,点B的坐标是(4,-1),点A与点B关于x轴对称,则点A的坐标是( )
A. (4,1) B. (-1,4) C. (-4,-1) D. (-1,-4)
2.观察下列四个图案,可以发现它们具有一个共有的性质,
那么下面四个三位数形成的图案中,具有上述类似共有性质的一个三位数是( )
A. 228 B. 303 C. 808 D. 609
3.等腰三角形的一个角为40°,那么底角等于( )
A. 40° B. 100° C. 70 D. 40°或70°
4.如图所示,△ ABC中,AC=AD=BD , ∠DAC=80°,则∠B的度数为( )
A. 40° B. 35° C. 25° D. 20°
5.如图,已知等边 分别在 上,且 ,连接 交 点.则
A. 30° B. 45° C. 60° D. 80°
6.如图,∠C=90°,AD平分∠BAC交BC于D , 若BC=5 cm , BD=3 cm , 则点D到AB的距离为( )cm .
A. 3 B. 4 C. 2 D. 1
7.如图,△ ABC中,AB=AC,AD=DE, ∠BAD=18°,∠EDC=12°,则 ∠DAE的度数是 ( )
A. 52° B. 58° C. 60° D. 62°
8.如图,已知 ,以 两点为圆心,大于 的长为半径画圆弧,两弧相交于点 ,连接 与 相交于点 ,则 的周长为( )
A. 8 B. 9 C. 11 D. 13
9.如图,在等边△ ABC中,点E是AC边的中点,点P是△ ABC的中线AD上的动点,且AD=6,则PE+PC的最小值是 ( )
A. 12 B. 9 C. 6 D. 3
10.如图,在平面直角坐标系中,等腰直角三角形 OA1A2 的直角边 OA1 在 y轴的正半轴上,且 OA1=A1A2=1,以 OA2 为直角边作第二个等腰直角三角形 OA A3, 以 OA3为直角边作第三个等腰直角三角形OA3A4, …,依此规律,得到等腰直角三角形 OA2021A2022, 则点 A2021 的坐标为( )
A. (0,-21010) B. (-21010 , 0) C. (0,-21009) D. (-21009 , 0)
二、填空题(共4题;共20分)
11. AD,AE分别是等边三角形ABC的高和中线,则AD 与AE 的大小关系为 ________.
12. 如图,AD是等边三角形ABC的中线,AE=AD,则∠EDC= ________.
13. 如图,在△ ABC中,BD平分∠ABC,CE平分∠ACB,BD与CE交于点M.若MN⊥BC于N,∠A=60°,
则∠1-∠2 = 度.
14. 如图,等边△ A1C1C2的周长为1,作C1D1⊥ A1C2于D1 , 在C1C2的延长线上取点C3 , 使D1C3=D1C1 , 连接D1C3 , 以C2C3为边作等边△ A2C2C3;作C2D2⊥A2C3于D2 , 在C2C3的延长线上取点C4 , 使D2C4=D2C2 , 连接D2C4 , 以C3C4为边作等边△ A3C3C4;…且点A1 , A2 , A3 , …都在直线C1C2同侧,如此下去,可得到△ A1C1C2 , △ A2C2C3 , △ A3C3C4 , …,△ AnCnCn+1 , 则△ AnCnCn+1的周长
为________ (n≥1,且n为整数)。
三、解答题(共9题;共90分)
15.(8分)如图,在△ ABC中,D是BC边上一点,AD=BD=AC,∠BAC=630,求∠DAC的度数。
(第15题图) (第16题图)
16.(8分)如图,△ ABC是等边三角形,AD为中线,AD=AE,E在AC上,求∠EDC的度数。
17.(8分)如图,△ ABC中,BC=10,AB的垂直平分线分别交AB、BC于点D、E,A C的垂直平分线分别交A C、BC于点F、G.求△ AEG的周长.
18.(8分)如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
①请画出△ ABC关于y轴对称的△ A1B1C1;
②请画出△ ABC关于原点对称的△ A2B2C2;
③在x轴上求作一点P,使△ PAB的周长最小,请画出△ PAB,并直接写出点P的坐标。
19.(10分)如图,AC平分∠BAD,CE⊥ AB于E,CF⊥AD于F,且BC=DC。求证:BE=DF。
(第19题图) (第20题图)
20.(10分)如图,在△ ABC中,AB=AC,点E是AC上一点,ED⊥BC于点D,DE的延长线交BA的延长线于点F.求证:△ AEF是等腰三角形.
21.(12分)如图,已知AD为△ ABC的高,∠B = 2∠C,求证:CD = AB + BD .
(第21题图) (第22题图)
22.(12分)如图,点F是长方形ABCD的BC彼岸上一点,把这张长方形纸片ABCD沿直线AF折叠,已知∠ADB=20°,那么∠BAF应为多少度时,才能使AB′∥ BD ?
23.(14分)如图,△ABC中,AD⊥ BC于D,BD=AC+CD,若∠ BAC=100°,求∠ ACD的度数。
2021-2022学年度 初中数学 月考卷 答题卡
学校:___________姓名:___________班级:___________考号:___________
一、单选题(40分,每题5分)
1 2 3 4 5 6 7 8 9 10
二、填空题(20分,每题5分)
11题、
12题、
13题、
14题、
三、解答题(90分)
15题(8分)
16题(8分)
17题(8分)
18题(8分)
19题(10分)
20题(10分)
21题(12分)
22题(12分)
23题、
第15章 轴对称图形和等腰三角形 单元测试卷1(沪科版 八年级上册)
答案解析部分
一、单选题: ACDCC CDACA
1.【答案】 A
【解析】【解答】解:∵ 点B的坐标是(4,﹣1),点A与点B关于x轴对称,
∴ 点A的坐标是:(4,1).故答案为:A.
【分析】根据轴对称
2.【答案】 C
【解析】【解答】解:四个图形都是轴对称图形,只有三位数808组成的图案是轴对称图形.
故C符合题意. 故答案为:C.
【分析】根据轴对称图形的定义判断.如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形.
3.【答案】 D
【解析】【解答】首先要讨论40°的角是顶角还是底角,再利用等腰三角形的性质和三角形内角和定理求出底角.当等腰三角形的顶角为40°时,则底角等于70°;当等腰三角形的底角为40°时,则底角等于40°.故选D.
【分析】学会运用分类讨论的思想解决问题.熟练掌握等腰三角形的性质和三角形的内角和定理.
4.【答案】 C
【解析】【解答】解:∵ AC=AD , ∠DAC=80°, ∴ ∠ADC=∠C=50°,
∵ AD=BD , ∠ADC=∠B+∠BAD=50°,∴ ∠B=25°,故答案为:C.
【分析】先根据等腰三角形的性质及三角形的内角和定理求出∠ADC的度数,再根据等腰三角形的性质及三角形外角与内角的关系求出∠B的度数即可。
5.【答案】C ∵ 是等边三角形 ∴ ,
易知 ,∴
∴ .
【解析】【分析】利用SAS得出 , 是关键。
6.【答案】 C
【解析】【解答】解:作DE⊥ AB于E , 如下图,
∴ DE=CD=CD=2cm , 即点D到AB的距离为2cm , 故答案为:C .
【分析】过点D作DE⊥AB于E , 通过角平分线的性质进行求解即可得到点D到AB的距离.
7.【答案】 D
【解析】【解答】设∠ADE=x°,且∠BAD=18°,∠EDC=12°,
∴ ∠B+18°=x°+12°,∴ ∠B=x°-6°,
∵ AB=AC,∴ ∠C=∠B=x°-6°,∴ ∠DEA=∠C+∠EDC=x°-6°+12°=x°+6°,
∵ AD=DE,∴ ∠DEA=∠DAE=x°+6°,
在△ ADE中,由三角形内角和定理可得,x+x+6+x+6=180,解得x=56,即∠ADE=56°,∴ ∠DAE=62°
故答案为:D.
【分析】设∠ADE=x°,且∠BAD=18°,∠EDC=12°,根据三角形的外角可得∠B+18°=x°+12°,化简为∠B=x°-6°,再利用等边对等角的性质可得∠C=∠B=x°-6°,∠DEA=∠DAE=x°+6°,最后利用三角形的内角和
8.【答案】 A
【解析】【解答】解:由作法得 垂直平分 (线段垂直平分线的定义),
的周长 ,
故答案为:A.
【分析】利用线段垂直平分线的性质可证得DA=DB,再证明△ BDC的周长=AC+BC,然后代入计算.
9.【答案】 C 【解析】【解答】解:
连BP,则由△PBD与△ PCD 全等,可得 PC=PB,于是 PE+PC=PE+PB
两点直角选段最短,故当B、P、E共线时,PE+PC 最短,为 BE的长,而在同一等边三角形中,
三边上的高相等,故 BE=AD=6, 故答案为:C.
【分析】根据题意,求PE+PC的最小值,将其转化为PE+PCP的值是关键。
10.【答案】 A
【解析】【解答】解:∵ 等腰直角三角形 的直角边 在y轴的正半轴上,且 ,以 为直角边作第二个等腰直角三角形 ,以 为直角边作等腰直角三角形 …
∴ , , ,…, ,
∵ 、 、 …每8个一循环,再回到y轴的正半轴,
,
∴ 点 在y轴的负半轴上,
∵ ,
∴ .
故答案为:A.
【分析】先根据等腰直角三角形的性质发现 , , ,…, 的规律,再根据8个点一循环,确定 的位置,得到它的点坐标.
二、填空题
11.【答案】 相等
【解析】【解答】根据等边三角形三线合一的性质,可以求得等边三角形每个内角的角平分线和其对应边的中线、高线重合,所以AD 与AE相等
【分析】根据等腰三角形三线合一和等边三角形是特殊的等腰三角形可求解.
12.【答案】 15°
【解析】【解答】解:∵ AD是等边△ ABC的中线,
∴ AD⊥BC,∠BAD=∠CAD= ∠BAC= ×60°=30°,∴ ∠ADC=90°,
∵ AD=AE,∴ ∠ADE=∠AED= =75°,∴ ∠EDC=∠ADC-∠ADE=90°-75°=15°.
故答案为:15°.
【分析】根据等边三角形的性质得出AD⊥BC,∠CAD= 30°,进而根据等边对等角及三角形的内角和定理即可算出∠ADE的度数,最后根据∠EDC=∠ADC-∠ADE即可算出答案.
13.【答案】 30
【解析】【解答】解:∵ ∠BMC=180°- (∠ABC+∠ACB)=180°- (180°-∠A)=90°+ ∠A=120°,
∴ ∠1+∠BMN=120°①,
∵ MN⊥BC,∴ ∠2+∠BMN=90°②,
①-②得:∠1-∠2=30°.故答案为:30.
【分析】根据外角平分线的性质,可通过角的运算得出∠1-∠2的度数。
14.【答案】
【解析】【解答】解: 等边三角形 的周长为1,作 于点 ,
,,
,
的周长= 的周长= ,
的周长分别为
故答案为:
【分析】利用等边三角形的性质和特殊角去解题.
三、解答题
15.【答案】 ∵ AD=BD=CA,
由图可知,∠3=∠1+∠2,∠3=∠4,∠1=∠2,∠BAC=63°,∴ ∠4=∠1+∠2=2∠2,
∵ ∠BAC+∠2+∠4=180°,即3∠2+63°=180°,∴ ∠2=39°,∠DAC=∠BAC-∠1=63°-39°=24°.
【解析】【分析】 由等腰三角形的性质及三角形外角的性质可得∠3=∠1+∠2,∠3=∠4,∠1=∠2,在△ ACD中,利用三角形的内角和可得∠BAC+∠2+∠4=180°, 据此求出∠2的度数,即得∠1的度数,根据∠DAC=∠BAC-∠1即可求解.
16.【答案】 解:∵ △ ABC是等边三角形,AD为中线, ∴ AD⊥BC,∠CAD=30°,
∵ AD=AE,∴ ∠ADE=∠AED= = =75°,∴ ∠EDC=∠ADC﹣∠ADE=90°﹣75°=15°.
【解析】【分析】先根据△ ABC是等边三角形,AD为中线可得出AD⊥BC,∠CAD=30°,再由AD=AE可知∠ADE=∠AED,根据三角形内角和定理即可求出∠ADE的度数,故可得出∠EDC的度数.
17.【答案】 解:∵ DE垂直平分AB.∴ AE=BE.同理AG=CG.∴ △ AEG的周长=AE+AG+GE=BE+CG+GE=BC=10.
【解析】【分析】由于DE为AB的中垂线,则AE=BE,又由于FG是AC的中垂线,则AG=GC,△ AEG的周长等于AE+EG+GA也就是等于BE+EG+GC=BC从而可求出△ AEG的周长
18.【答案】 解:△ A1B1C1、△ A2B2C2、△ PAB如图所示,P(2,0)
【解析】【分析】(1)根据关于y轴对称的点的坐标的变化规律:横坐标变为原来的相反数,纵坐标不变,求出A、B、C的对应点的坐标,再在平面直角坐标系中画出图形即可;
(2)根据关于原点对称的点的坐标的变化规律:横坐标与纵坐标都变为原来的相反数,求出A、B、C的对应点的坐标,再在平面直角坐标系中画出图形即可;
(3)找出点A关于x轴的对称点,再将B连接起来与x轴的交点即为点P。
19.【答案】 解:∵ AC平分∠BAD,∴ ∠1=∠2
∵ CE⊥AB于E,CF⊥AD于F,∴ CE=CF
∵ 在Rt△ DCF与Rt△ ECB中,CE=CF, BC=DC,∴ Rt△ DCF≌Rt△ ECB(HL),∴ BE=DF
【解析】【分析】根据角平分线的性质得出CE=CF,然后根据HL证得Rt△ DCF与Rt△ ECB全等,即可证明BE=DF。
20.【答案】 解:DF⊥BC,∴ ∠B+∠F=90°,∠C+∠DEC=90°,∵ AB= AC,∴ ∠B=∠C,∴ ∠F=∠DEC,∵ ∠AEF =∠DEC,∴ ∠F=∠AEF,∴ AE = AF, ∴ AEF是等腰三角形.
【解析】【分析】根据题意,由三角形的内角和定理以及等量代换,证明三角形为等腰三角形即可。
21.【答案】 证明:在DC取点E,使DE=BD,连接AE,
∵ AD为△ ABC的高,∴ AD⊥BE,∴ AB=AE,∴ ∠AEB=∠B,
又∵ ∠B=2∠C,∴ ∠AEB=2∠C,
∵ ∠AEB=∠C+∠EAC,∴ ∠C=∠EAC,∴ AE=EC=AB,
∵ CD=DE+EC,BD=DE,∴ CD=AB+BD.
【解析】【分析】在DC取点E,使DE=BD,连接AE,根据线段垂直平分线求出AB=AE,推出∠B=∠AEB=2∠C=∠C+∠EAC,推出∠C=∠EAC,推出AE=EC=AB,代入即可求出答案.
22.【答案】 ∠BAF应为55度
理由是:∵ ∠ADB = 20°,四边形ABCD是长方形,∴ ∠ABD =70°.
∵ 要 使AB′∥ BD,需使∠BAB′= 110°,由折叠可知∠BAF = ∠B′AF,∴ ∠BAF应为55度
【解析】【分析】先根据直角三角形的性质求出∠ABD的度数,再由平行线的性质求出∠BAB′的度数,根据图形翻折变换的性质即可得出结论.
23.【答案】 解:如图,以A为圆心,AC长为半径画弧,交BC于点E,连接AE,
则AE=AC,CD=DE,∠ CAD=∠ EAD,又BD=AC+DC,BD=BE+DE,
∴ AE=AC=BE,∴ ∠ B=∠ BAE
设∠ ACD=x,则∠ CAD=90°-x,∠ B=∠ BAE=100°-2(90°-x)=100°-180°+2x=2x-80°,
故 ∠AED=2∠B=4x-160°,
在三角形AEC中,由三角形内角和定理得:x+2(90°-x)+(4x-160°)=180°,解得:x= .
【解析】【分析】 以A为圆心,AC长为半径画弧,交BC于点E,连接AE,由等腰三角形的性质可得 CD=DE , ∠CAD=∠EAD , 进而得出 AE=AC=BE ,根据等边对等角得出 ∠B=∠BAE ,并设∠C=x,然后用含x的式子表示出∠CAD及∠B与∠BAE,最后根据三角形的内角和定理列出方程,解方程可以得到∠C的度数.
【解法二】在DC延长线上,截取一段CF=CA。7
