2021-2022学年七年级数学人教版上册期末复习 第四章几何图形初步过关习题(word版含答案)
文档属性
| 名称 | 2021-2022学年七年级数学人教版上册期末复习 第四章几何图形初步过关习题(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 253.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-31 19:51:16 | ||
图片预览

文档简介
七年级上册数学
期末复习——第四章过关A卷
一、选择题(下列各题的四个选项中,只有一项符合题目要求。每题3分,共30分)
1.下列几何体中,面的个数最少的为( )
A. B.
C. D.
2.与图中实物图相类似的立体图形按从左到右的顺序依次是( )
A.圆柱、圆锥、正方体、长方体 B.圆柱、球、正方体、长方体
C.棱柱、球、正方体、棱柱 D.棱柱、圆锥、棱柱、长方体
3.如图是一个正方体的表面展开图,则原正方体标有数字“”所在面的对面标有的数字是( )
A. B. C. D.
4.用一个平面去截下列立体图形,截面可以得到三角形的立体图形有( )
A.1个 B.2个 C.3个 D.4个
5.已知线段AB=8,在直线AB上画线段AC,使AC=3,则线段BC等于( )
A.11 B.5
C.11或5 D.8或11
6.如图,线段CD在线段AB上,且CD =1,若AB的长度是一个正整数,则图中以A,B,C,D这四点中任意两点为端点的所有线段长度之和可能是( )
A.12 B.13 C.14 D.15
7.下面四个图形中,能用∠1,∠AOB,∠O三种方法表示同一个角的图形是( )
A. B.
C. D.
8.如图,点O在直线AB上,∠COB=∠DOE=90°,那么图中相等的角的对数和互余两角的对数分别为( )
A.7;5 B.5;4 C.4;4 D.3;3
9.下列图形中的两个角互为补角的是( )
A.①和② B.①和③ C.①和④ D.②和④
10.如图,已知点A是射线BE上一点,过A作AC⊥BF,垂足为C,CD⊥BE,垂足为D.给出下列结论:①∠1是∠ACD的余角;②图中互余的角共有3对;③∠1的补角只有∠DCF;④与∠ADC互补的角共有3个.其中正确结论有( )
A.① B.①②③ C.①④ D.②③④
二、填空题(每题3分,共15分)
11.已知,点C在线段AB上,AB=10cm,AC=4cm.则线段BC的长度等于______cm.
12.已知图1的小正方形和图2中所有的小正方形边长都相等,将图1的小正方形安放在图2中的①、②、③、④的其中某一个位置,放置后所组成的图形是围成一个正方体的.那么安放的位置不是是__________.
13.若一个三棱锥的顶点个数为m、它的棱数为n,则(m+n-9)2021的值为______.
14.如图,将三个同样的正方形的一个顶点重合放置,如果,时,那么的度数是___________度;
15.若,,则______.
三、解答题(共55分)
16.(6分)画图.如图在平面内有四个点A,B,C,D按下面的娶求作图(要求,利用尺规,不写画法,保留作图痕迹.不写结论)
①作直线AB;
②作线段AC;
③作射线AD、DC、CB;
17.(6分)从正面、左面、上面观察如图所示的几何体,分别面出你所看到的几何体的形状图.
18.(6分)已知∠AOB=110°,OC平分∠AOD,OE平分∠BOD,求∠COE的度数.
19.(8分)如图,点C为线段AD上一点,点B为CD的中点,且AD=13cm,BC=3cm.
(1)图中共有 条线段;
(2)求AC的长;
(3)若点E在直线AD上,且EA=4cm,求BE的长.
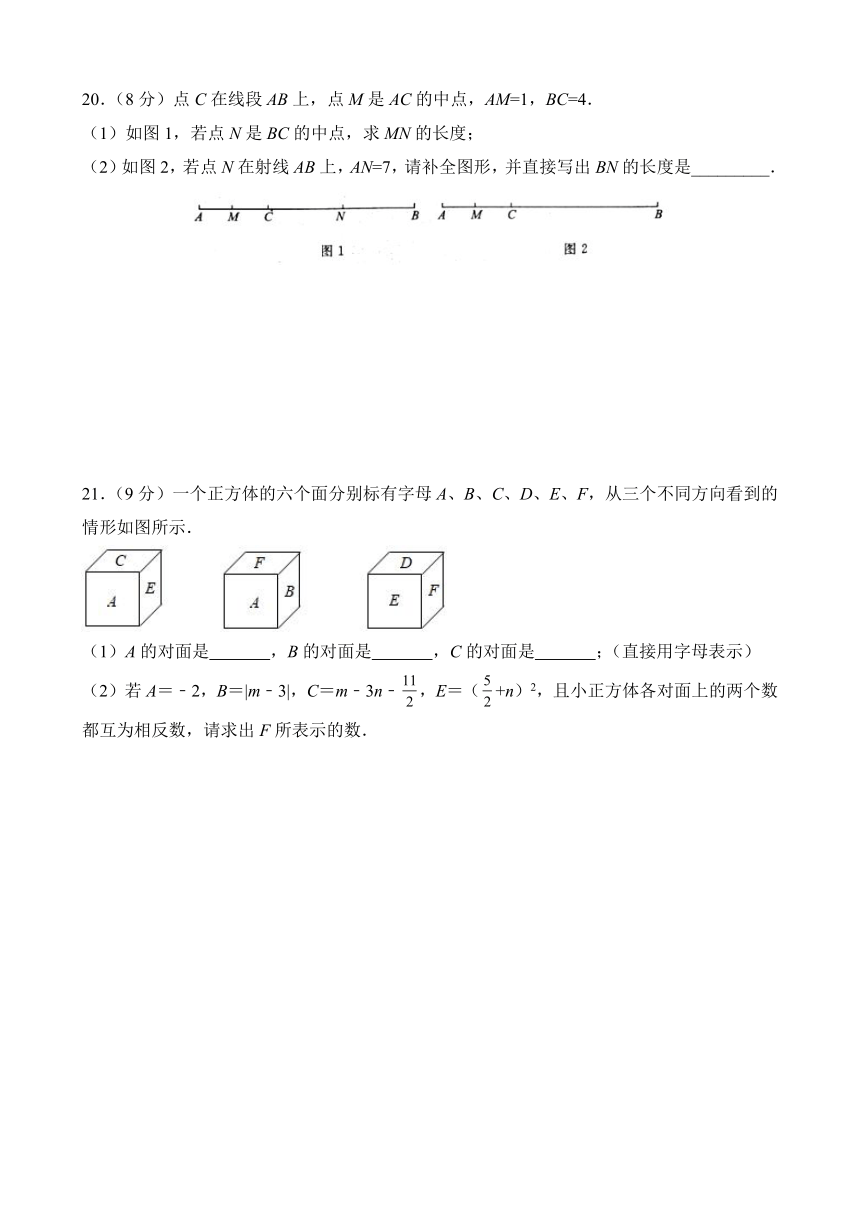
20.(8分)点C在线段AB上,点M是AC的中点,AM=1,BC=4.
(1)如图1,若点N是BC的中点,求MN的长度;
(2)如图2,若点N在射线AB上,AN=7,请补全图形,并直接写出BN的长度是_________.
21.(9分)一个正方体的六个面分别标有字母A、B、C、D、E、F,从三个不同方向看到的情形如图所示.
(1)A的对面是 ,B的对面是 ,C的对面是 ;(直接用字母表示)
(2)若A=﹣2,B=|m﹣3|,C=m﹣3n﹣,E=(+n)2,且小正方体各对面上的两个数都互为相反数,请求出F所表示的数.
22.(12分)已知,O是直线AB上的一点,OC⊥OE.
(1)如图①,若∠COA=34°,求∠BOE的度数.
(2)如图②,当射线OC在直线AB下方时,OF平分∠AOE,∠BOE=130°,求∠COF的度数.
(3)在(2)的条件下,如图③,在∠BOE内部作射线OM,使∠COM+∠AOE=2∠BOM+∠FOM,求∠BOM的度数.
【参考答案】
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 B B B C C B B B C C
二、填空题
11.6 12.① 13.1 14.27 15.102°32′
三、解答题
16.如图所示:
17.如图所示:
18.解:∵∠AOB=110°,OC平分∠AOD,OE平分∠BOD,
∴.
19.解:(1)6;
(2)∵点B为CD的中点,BC=3cm,
∴CD=2BC=6cm.
∵AD=13cm,
∴AC=AD-CD=13-6=7(cm);
(3)分两种情况讨论:
①如图(1),当点E在AC上时,
∵AB=AC+BC=10 cm,EA=4cm,
∴BE=AB-AE=10-4=6(cm);
②如图(2),当点E在CA延长线上时,
∵AB=10cm,AE=4cm,
∴BE=AE+AB=14(cm);
综上,BE的长为6cm或14cm.
20.解:(1)点是的中点,,
,
点是的中点,,
,
;
(2)1.
21.解:(1)D,E,F;
(2)∵字母A表示的数与它对面的字母D表示的数互为相反数,
∴|m﹣3|+(+n)2=0,
∴m﹣3=0,+n=0,
解得m=3,n=﹣,
∴C=m﹣3n﹣=3﹣3×(﹣)﹣=5,
∴F所表示的数是﹣5.
22.(1)∵OC⊥OE,∠COA=34°,
∴∠BOE=180°-90°-34°=56°;
(2)∵∠BOE=130°,
∴∠AOE=180°-∠BOE=50°
∵OF平分∠AOE,
∴∠EOF=∠AOE=25°=∠AOF
∵OC⊥OE.
∴∠COF=90°-∠EOF=65°;
(3)∵OC⊥OE,
∴∠AOC=90°-∠AOE=40°
设∠BOM的度数为x
∴∠COM=∠AOC+∠AOM=40°+180°-x=220°-x,∠FOM=∠AOM-∠AOF=180°-x-25°=155°-x
∵∠COM+∠AOE=2∠BOM+∠FOM,
∴220°-x+×50°=2x+155°-x
解得x=75°
∴∠BOM的度数为75°.
期末复习——第四章过关A卷
一、选择题(下列各题的四个选项中,只有一项符合题目要求。每题3分,共30分)
1.下列几何体中,面的个数最少的为( )
A. B.
C. D.
2.与图中实物图相类似的立体图形按从左到右的顺序依次是( )
A.圆柱、圆锥、正方体、长方体 B.圆柱、球、正方体、长方体
C.棱柱、球、正方体、棱柱 D.棱柱、圆锥、棱柱、长方体
3.如图是一个正方体的表面展开图,则原正方体标有数字“”所在面的对面标有的数字是( )
A. B. C. D.
4.用一个平面去截下列立体图形,截面可以得到三角形的立体图形有( )
A.1个 B.2个 C.3个 D.4个
5.已知线段AB=8,在直线AB上画线段AC,使AC=3,则线段BC等于( )
A.11 B.5
C.11或5 D.8或11
6.如图,线段CD在线段AB上,且CD =1,若AB的长度是一个正整数,则图中以A,B,C,D这四点中任意两点为端点的所有线段长度之和可能是( )
A.12 B.13 C.14 D.15
7.下面四个图形中,能用∠1,∠AOB,∠O三种方法表示同一个角的图形是( )
A. B.
C. D.
8.如图,点O在直线AB上,∠COB=∠DOE=90°,那么图中相等的角的对数和互余两角的对数分别为( )
A.7;5 B.5;4 C.4;4 D.3;3
9.下列图形中的两个角互为补角的是( )
A.①和② B.①和③ C.①和④ D.②和④
10.如图,已知点A是射线BE上一点,过A作AC⊥BF,垂足为C,CD⊥BE,垂足为D.给出下列结论:①∠1是∠ACD的余角;②图中互余的角共有3对;③∠1的补角只有∠DCF;④与∠ADC互补的角共有3个.其中正确结论有( )
A.① B.①②③ C.①④ D.②③④
二、填空题(每题3分,共15分)
11.已知,点C在线段AB上,AB=10cm,AC=4cm.则线段BC的长度等于______cm.
12.已知图1的小正方形和图2中所有的小正方形边长都相等,将图1的小正方形安放在图2中的①、②、③、④的其中某一个位置,放置后所组成的图形是围成一个正方体的.那么安放的位置不是是__________.
13.若一个三棱锥的顶点个数为m、它的棱数为n,则(m+n-9)2021的值为______.
14.如图,将三个同样的正方形的一个顶点重合放置,如果,时,那么的度数是___________度;
15.若,,则______.
三、解答题(共55分)
16.(6分)画图.如图在平面内有四个点A,B,C,D按下面的娶求作图(要求,利用尺规,不写画法,保留作图痕迹.不写结论)
①作直线AB;
②作线段AC;
③作射线AD、DC、CB;
17.(6分)从正面、左面、上面观察如图所示的几何体,分别面出你所看到的几何体的形状图.
18.(6分)已知∠AOB=110°,OC平分∠AOD,OE平分∠BOD,求∠COE的度数.
19.(8分)如图,点C为线段AD上一点,点B为CD的中点,且AD=13cm,BC=3cm.
(1)图中共有 条线段;
(2)求AC的长;
(3)若点E在直线AD上,且EA=4cm,求BE的长.
20.(8分)点C在线段AB上,点M是AC的中点,AM=1,BC=4.
(1)如图1,若点N是BC的中点,求MN的长度;
(2)如图2,若点N在射线AB上,AN=7,请补全图形,并直接写出BN的长度是_________.
21.(9分)一个正方体的六个面分别标有字母A、B、C、D、E、F,从三个不同方向看到的情形如图所示.
(1)A的对面是 ,B的对面是 ,C的对面是 ;(直接用字母表示)
(2)若A=﹣2,B=|m﹣3|,C=m﹣3n﹣,E=(+n)2,且小正方体各对面上的两个数都互为相反数,请求出F所表示的数.
22.(12分)已知,O是直线AB上的一点,OC⊥OE.
(1)如图①,若∠COA=34°,求∠BOE的度数.
(2)如图②,当射线OC在直线AB下方时,OF平分∠AOE,∠BOE=130°,求∠COF的度数.
(3)在(2)的条件下,如图③,在∠BOE内部作射线OM,使∠COM+∠AOE=2∠BOM+∠FOM,求∠BOM的度数.
【参考答案】
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 B B B C C B B B C C
二、填空题
11.6 12.① 13.1 14.27 15.102°32′
三、解答题
16.如图所示:
17.如图所示:
18.解:∵∠AOB=110°,OC平分∠AOD,OE平分∠BOD,
∴.
19.解:(1)6;
(2)∵点B为CD的中点,BC=3cm,
∴CD=2BC=6cm.
∵AD=13cm,
∴AC=AD-CD=13-6=7(cm);
(3)分两种情况讨论:
①如图(1),当点E在AC上时,
∵AB=AC+BC=10 cm,EA=4cm,
∴BE=AB-AE=10-4=6(cm);
②如图(2),当点E在CA延长线上时,
∵AB=10cm,AE=4cm,
∴BE=AE+AB=14(cm);
综上,BE的长为6cm或14cm.
20.解:(1)点是的中点,,
,
点是的中点,,
,
;
(2)1.
21.解:(1)D,E,F;
(2)∵字母A表示的数与它对面的字母D表示的数互为相反数,
∴|m﹣3|+(+n)2=0,
∴m﹣3=0,+n=0,
解得m=3,n=﹣,
∴C=m﹣3n﹣=3﹣3×(﹣)﹣=5,
∴F所表示的数是﹣5.
22.(1)∵OC⊥OE,∠COA=34°,
∴∠BOE=180°-90°-34°=56°;
(2)∵∠BOE=130°,
∴∠AOE=180°-∠BOE=50°
∵OF平分∠AOE,
∴∠EOF=∠AOE=25°=∠AOF
∵OC⊥OE.
∴∠COF=90°-∠EOF=65°;
(3)∵OC⊥OE,
∴∠AOC=90°-∠AOE=40°
设∠BOM的度数为x
∴∠COM=∠AOC+∠AOM=40°+180°-x=220°-x,∠FOM=∠AOM-∠AOF=180°-x-25°=155°-x
∵∠COM+∠AOE=2∠BOM+∠FOM,
∴220°-x+×50°=2x+155°-x
解得x=75°
∴∠BOM的度数为75°.
