2021-2022学年人教版七年级上册数学期末复习第四章几何图形初步过关B卷(Word版含简答)
文档属性
| 名称 | 2021-2022学年人教版七年级上册数学期末复习第四章几何图形初步过关B卷(Word版含简答) |  | |
| 格式 | doc | ||
| 文件大小 | 365.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-31 23:50:14 | ||
图片预览



文档简介
七年级上册数学
期末复习——第四章过关B卷
一、选择题(下列各题的四个选项中,只有一项符合题目要求。每题3分,共30分)
1.如图是一个小正方体的展开图,把展开图折叠成小正方体后,有“建”字一面的相对面上的字是( )
A.和 B.谐 C.社 D.会
2.一个正方体,六个面上分别写着六个连续的整数,且每两个相对面上的两个数之和相等,如图你能看到的数为7、10、11,则这六个整数的和可能为( ).
A.51 B.53 C.55 D.57
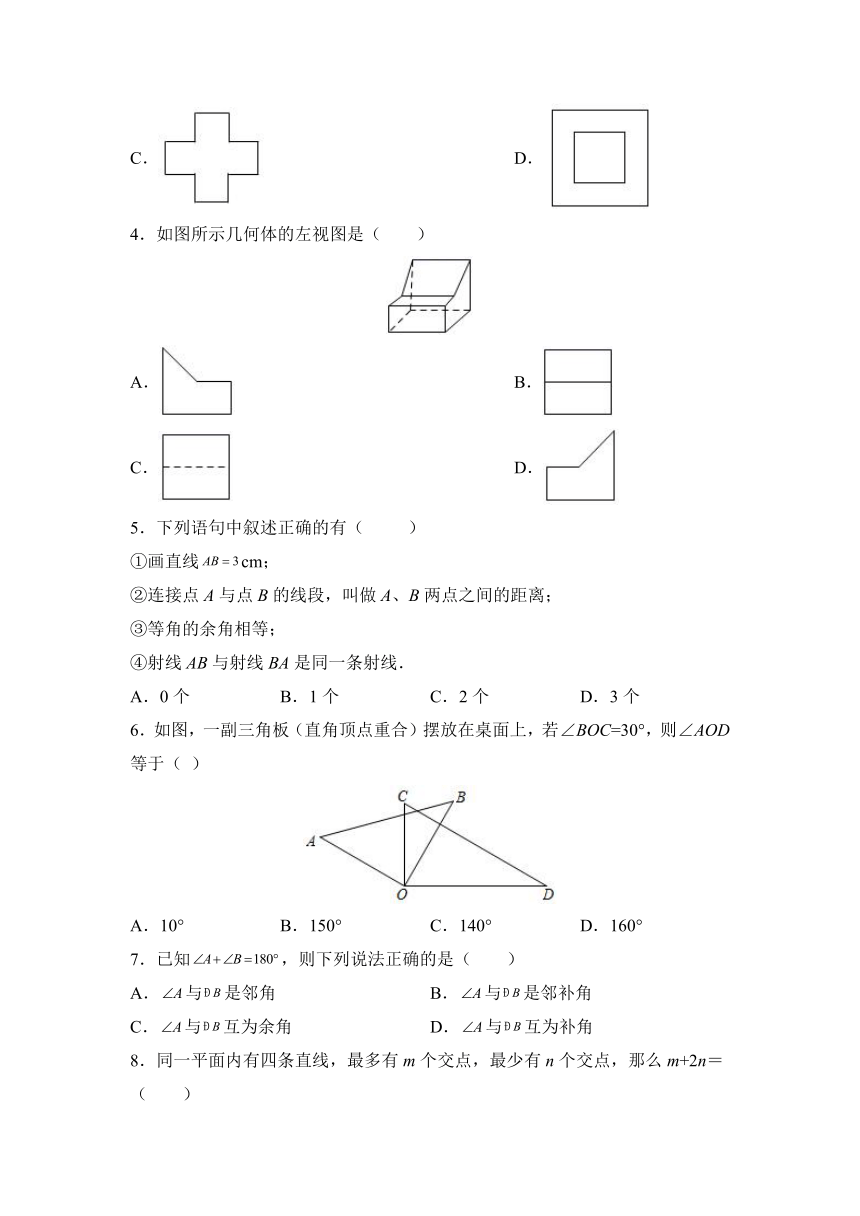
3.将一正方形纸片按下列顺序折叠,然后将最后折叠的纸片沿虚线剪去右上方的小三角形.将纸片展开,得到的图形是( )
B.
C. D.
4.如图所示几何体的左视图是( )
B.
C. D.
5.下列语句中叙述正确的有( )
①画直线cm;
②连接点A与点B的线段,叫做A、B两点之间的距离;
③等角的余角相等;
④射线AB与射线BA是同一条射线.
A.0个 B.1个 C.2个 D.3个
6.如图,一副三角板(直角顶点重合)摆放在桌面上,若∠BOC=30°,则∠AOD等于( )
A.10° B.150° C.140° D.160°
7.已知,则下列说法正确的是( )
A.与是邻角 B.与是邻补角
C.与互为余角 D.与互为补角
8.同一平面内有四条直线,最多有m个交点,最少有n个交点,那么m+2n=( )
A.1 B.6 C.8 D.4
9.已知线段,点是直线上一点,,点是线段的中点,点是线段的中点,则线段的长度是( )
A. B.
C.或 D.或
10.已知射线在的内部,下列4个表述中:①;②;③;④,能表示射线是的角平分线的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(每题3分,共15分)
11.如图,O是AB上一点,OD平分∠BOC,∠1=20°,∠2的度数是__________.
12.一个角为57°13′、则它的补角等于________.
13.如图,已知线段,点是线段靠近点的四等分点,点是线段的中点,则线段______
14.如图,在正方形ABCD中,E为DC边上一点,沿线段BE对折后,若比大18°,则的度数是___________________度.
15.若将一幅三角板按如图放置,下列结论:①;②若,则;③若,则;④若,则.其中正确的序号有______.
三、解答题(共55分)
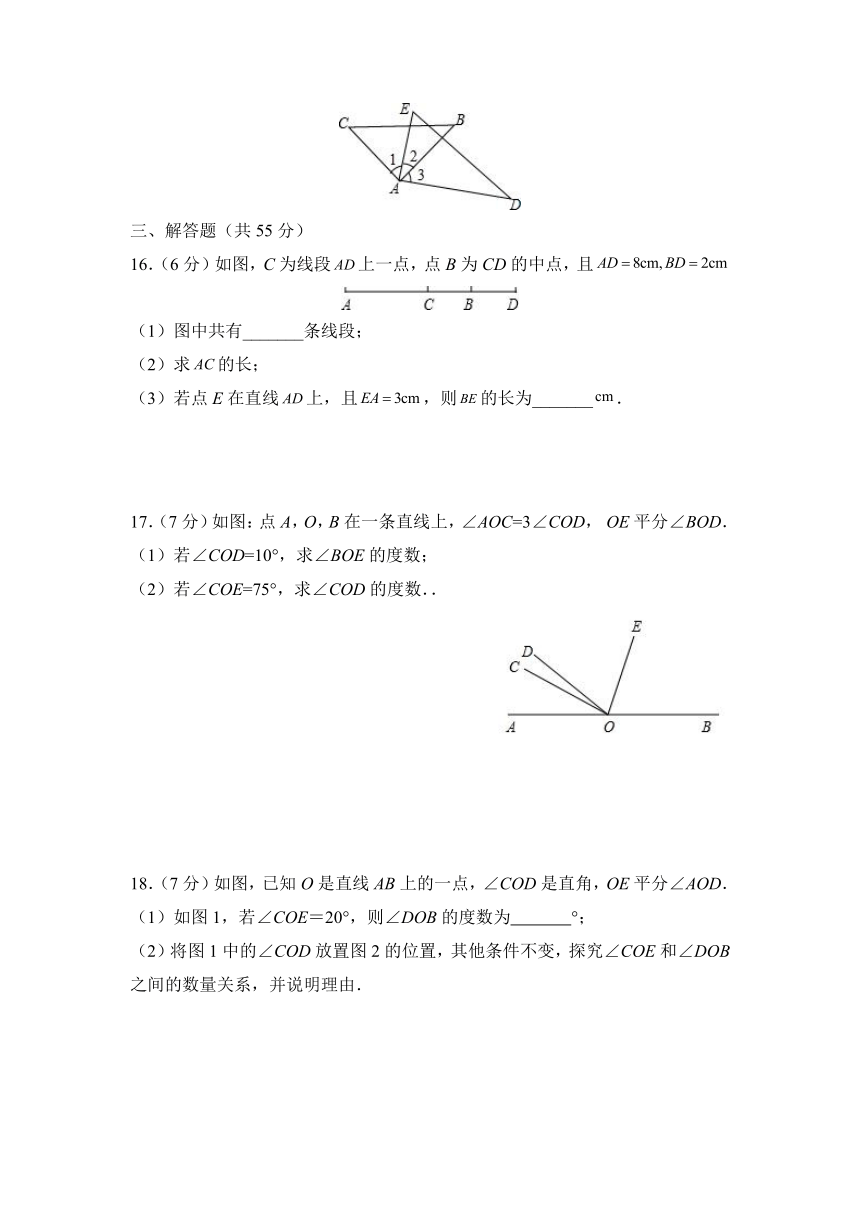
16.(6分)如图,C为线段上一点,点B为CD的中点,且
(1)图中共有_______条线段;
(2)求的长;
(3)若点E在直线上,且,则的长为_______.
17.(7分)如图:点A,O,B在一条直线上,∠AOC=3∠COD, OE平分∠BOD.
(1)若∠COD=10°,求∠BOE的度数;
(2)若∠COE=75°,求∠COD的度数..
18.(7分)如图,已知O是直线AB上的一点,∠COD是直角,OE平分∠AOD.
(1)如图1,若∠COE=20°,则∠DOB的度数为 °;
(2)将图1中的∠COD放置图2的位置,其他条件不变,探究∠COE和∠DOB之间的数量关系,并说明理由.
19.(6分)如图,已知线段AB.
(1)利用刻度尺画图:延长线段AB至C,使BC=AB,取线段AC的中点D.
(2)若CD=6,求线段BD的长.
20.(8分)如图,已知直线AB及直线AB外一点P,按下列要求完成画图:
(1)画射线PA;
(2)在直线AB上作线段AC,使AC=AB-PB;
(3)画线段PB,并延长线段PB到点E,使BE=PB.
21.(9分)在水平的桌面上,由若干个完全相同棱长为10cm的小正方体堆成一个几何体,如图所示.
(1)请你在方格纸中分别画出这个几何体的主视图、左视图和俯视图;
(2)若现在手头还有一些相同的小正方体,如果保持这个几何体的左视图和俯视图不变,在这个几何体上最多可以添加多少个小正方体?
(3)若给该几何体露在外面的面喷上红漆(不含几何体的底面),则需要喷漆的面积是多少cm2?
22.(12分)已知为直线上的一点,是直角,平分.
(1)如图1,若,则 ;
(2)当射线绕点逆时针旋转到如图2的位置时,与之间有何数量关系?请说明理由.
(3)在图3中,若,在的内部是否存在一条射线,使得?若存在,请求出的度数;若不存在,请说明理由.
【参考答案】
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 D D A A B B D B C C
二、填空题
11.80° 12.122°47′ 13.30 14.24 15.①②④
三、解答题
16.解:(1)6;
(2)∵点B为CD的中点.
∴CD=2BD.
∵BD=2cm,
∴CD=4cm.
∵AC=AD-CD且AD=8cm,CD=4cm,
∴AC=4cm;
(3)3或9.
17.解:(1)∵∠COD=10°,
∴∠AOC=3∠COD=30°,∠AOD=∠AOC+∠COD=40°,
∵点A,O,B在一条直线上,
∴∠BOD=180°-∠AOD=140°,
又OE平分∠BOD,
∴∠BOE=∠BOD=70°;
(2)设∠COD的度数为x,则∠AOC=3x,∠EOD=∠COE-∠COD=75°-x,
∴∠BOD=2∠EOD=150°-2x,
∵点A,O,B在一条直线上,
∴∠BOD+∠AOD=180°,
即150°-2x+3x+x=180°,
解得x=15°,即∠COD=15°.
18.解:(1)40.
(2)∠DOB=2∠COE.
∵∠COD是直角,OE平分∠AOD,
∴∠DOE=∠AOD,
∴∠COE=∠COD﹣∠DOE=90°﹣∠AOD,
∴∠AOD=180°﹣2∠COE,
∴∠DOB=180°﹣∠AOD
=180°﹣(180°﹣2∠COE)
=2∠COE.
19.解:(1)如图,线段BC,中点D即为所求作.
(2)∵D是AC的中点,
∴AD=CD=6,
∴AC=12,
∴BC=AB,
∴BC=AC=4,
∴BD=CD-CB=6-4=2.
20.解:(1)如图所示:射线PA即为所求
(2)线段AC即为所求;
以B为圆心,以BP的长为半径画弧与AB交于C,线段AC即为所求;
(3)如图所示线段PB和E即为所求;
如图,连接PB,以B为圆心,以BP的长为半径画弧与PB的延长线交于E,即为所求.
21.解:(1)这个几何体的主视图和左视图如图:
(2)保持俯视图和左视图不变,可往第二列前面的几何体上放2个小正方体,后面的几何体上放1个小正方体,故最多可再添加3个正方体,
故答案为:3;
(3)10[(6+6)+6+2]=3200cm2
答:需要喷漆的面积是3200cm2.
22.解:(1)∵∠COF=28°,∠COE=90°,
∴∠EOF=90°﹣28°=62°,
∵OF平分∠AOE,
∴∠AOE=2∠EOF=124°,
∴∠BOE=180°﹣∠AOE=56°;
(2)结论:∠BOE=2∠COF;
理由如下:
∵∠COE=90°,
∴∠EOF=90°﹣∠COF,
∵OF平分∠AOE,
∴∠AOE=2∠EOF=180°﹣2∠COF,
∴∠BOE=180°﹣∠AOE=180°﹣(180°﹣2∠COF)=2∠COF;
(3)存在;
∵∠COF=65°,∠COE=90°,
∠EOF=25°,
∵OF平分∠AOE,∴∠AOF=∠EOF=25°,
∴∠BOE=130°,
∵2∠BOD+∠AOF=(∠BOE﹣∠BOD),
即2∠BOD+25°=(130°﹣∠BOD),解得∠BOD=16°.
期末复习——第四章过关B卷
一、选择题(下列各题的四个选项中,只有一项符合题目要求。每题3分,共30分)
1.如图是一个小正方体的展开图,把展开图折叠成小正方体后,有“建”字一面的相对面上的字是( )
A.和 B.谐 C.社 D.会
2.一个正方体,六个面上分别写着六个连续的整数,且每两个相对面上的两个数之和相等,如图你能看到的数为7、10、11,则这六个整数的和可能为( ).
A.51 B.53 C.55 D.57
3.将一正方形纸片按下列顺序折叠,然后将最后折叠的纸片沿虚线剪去右上方的小三角形.将纸片展开,得到的图形是( )
B.
C. D.
4.如图所示几何体的左视图是( )
B.
C. D.
5.下列语句中叙述正确的有( )
①画直线cm;
②连接点A与点B的线段,叫做A、B两点之间的距离;
③等角的余角相等;
④射线AB与射线BA是同一条射线.
A.0个 B.1个 C.2个 D.3个
6.如图,一副三角板(直角顶点重合)摆放在桌面上,若∠BOC=30°,则∠AOD等于( )
A.10° B.150° C.140° D.160°
7.已知,则下列说法正确的是( )
A.与是邻角 B.与是邻补角
C.与互为余角 D.与互为补角
8.同一平面内有四条直线,最多有m个交点,最少有n个交点,那么m+2n=( )
A.1 B.6 C.8 D.4
9.已知线段,点是直线上一点,,点是线段的中点,点是线段的中点,则线段的长度是( )
A. B.
C.或 D.或
10.已知射线在的内部,下列4个表述中:①;②;③;④,能表示射线是的角平分线的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(每题3分,共15分)
11.如图,O是AB上一点,OD平分∠BOC,∠1=20°,∠2的度数是__________.
12.一个角为57°13′、则它的补角等于________.
13.如图,已知线段,点是线段靠近点的四等分点,点是线段的中点,则线段______
14.如图,在正方形ABCD中,E为DC边上一点,沿线段BE对折后,若比大18°,则的度数是___________________度.
15.若将一幅三角板按如图放置,下列结论:①;②若,则;③若,则;④若,则.其中正确的序号有______.
三、解答题(共55分)
16.(6分)如图,C为线段上一点,点B为CD的中点,且
(1)图中共有_______条线段;
(2)求的长;
(3)若点E在直线上,且,则的长为_______.
17.(7分)如图:点A,O,B在一条直线上,∠AOC=3∠COD, OE平分∠BOD.
(1)若∠COD=10°,求∠BOE的度数;
(2)若∠COE=75°,求∠COD的度数..
18.(7分)如图,已知O是直线AB上的一点,∠COD是直角,OE平分∠AOD.
(1)如图1,若∠COE=20°,则∠DOB的度数为 °;
(2)将图1中的∠COD放置图2的位置,其他条件不变,探究∠COE和∠DOB之间的数量关系,并说明理由.
19.(6分)如图,已知线段AB.
(1)利用刻度尺画图:延长线段AB至C,使BC=AB,取线段AC的中点D.
(2)若CD=6,求线段BD的长.
20.(8分)如图,已知直线AB及直线AB外一点P,按下列要求完成画图:
(1)画射线PA;
(2)在直线AB上作线段AC,使AC=AB-PB;
(3)画线段PB,并延长线段PB到点E,使BE=PB.
21.(9分)在水平的桌面上,由若干个完全相同棱长为10cm的小正方体堆成一个几何体,如图所示.
(1)请你在方格纸中分别画出这个几何体的主视图、左视图和俯视图;
(2)若现在手头还有一些相同的小正方体,如果保持这个几何体的左视图和俯视图不变,在这个几何体上最多可以添加多少个小正方体?
(3)若给该几何体露在外面的面喷上红漆(不含几何体的底面),则需要喷漆的面积是多少cm2?
22.(12分)已知为直线上的一点,是直角,平分.
(1)如图1,若,则 ;
(2)当射线绕点逆时针旋转到如图2的位置时,与之间有何数量关系?请说明理由.
(3)在图3中,若,在的内部是否存在一条射线,使得?若存在,请求出的度数;若不存在,请说明理由.
【参考答案】
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 D D A A B B D B C C
二、填空题
11.80° 12.122°47′ 13.30 14.24 15.①②④
三、解答题
16.解:(1)6;
(2)∵点B为CD的中点.
∴CD=2BD.
∵BD=2cm,
∴CD=4cm.
∵AC=AD-CD且AD=8cm,CD=4cm,
∴AC=4cm;
(3)3或9.
17.解:(1)∵∠COD=10°,
∴∠AOC=3∠COD=30°,∠AOD=∠AOC+∠COD=40°,
∵点A,O,B在一条直线上,
∴∠BOD=180°-∠AOD=140°,
又OE平分∠BOD,
∴∠BOE=∠BOD=70°;
(2)设∠COD的度数为x,则∠AOC=3x,∠EOD=∠COE-∠COD=75°-x,
∴∠BOD=2∠EOD=150°-2x,
∵点A,O,B在一条直线上,
∴∠BOD+∠AOD=180°,
即150°-2x+3x+x=180°,
解得x=15°,即∠COD=15°.
18.解:(1)40.
(2)∠DOB=2∠COE.
∵∠COD是直角,OE平分∠AOD,
∴∠DOE=∠AOD,
∴∠COE=∠COD﹣∠DOE=90°﹣∠AOD,
∴∠AOD=180°﹣2∠COE,
∴∠DOB=180°﹣∠AOD
=180°﹣(180°﹣2∠COE)
=2∠COE.
19.解:(1)如图,线段BC,中点D即为所求作.
(2)∵D是AC的中点,
∴AD=CD=6,
∴AC=12,
∴BC=AB,
∴BC=AC=4,
∴BD=CD-CB=6-4=2.
20.解:(1)如图所示:射线PA即为所求
(2)线段AC即为所求;
以B为圆心,以BP的长为半径画弧与AB交于C,线段AC即为所求;
(3)如图所示线段PB和E即为所求;
如图,连接PB,以B为圆心,以BP的长为半径画弧与PB的延长线交于E,即为所求.
21.解:(1)这个几何体的主视图和左视图如图:
(2)保持俯视图和左视图不变,可往第二列前面的几何体上放2个小正方体,后面的几何体上放1个小正方体,故最多可再添加3个正方体,
故答案为:3;
(3)10[(6+6)+6+2]=3200cm2
答:需要喷漆的面积是3200cm2.
22.解:(1)∵∠COF=28°,∠COE=90°,
∴∠EOF=90°﹣28°=62°,
∵OF平分∠AOE,
∴∠AOE=2∠EOF=124°,
∴∠BOE=180°﹣∠AOE=56°;
(2)结论:∠BOE=2∠COF;
理由如下:
∵∠COE=90°,
∴∠EOF=90°﹣∠COF,
∵OF平分∠AOE,
∴∠AOE=2∠EOF=180°﹣2∠COF,
∴∠BOE=180°﹣∠AOE=180°﹣(180°﹣2∠COF)=2∠COF;
(3)存在;
∵∠COF=65°,∠COE=90°,
∠EOF=25°,
∵OF平分∠AOE,∴∠AOF=∠EOF=25°,
∴∠BOE=130°,
∵2∠BOD+∠AOF=(∠BOE﹣∠BOD),
即2∠BOD+25°=(130°﹣∠BOD),解得∠BOD=16°.
