上海市虹口区2020-2021学年七年级上学期期末联考数学试卷(Word版 含答案)
文档属性
| 名称 | 上海市虹口区2020-2021学年七年级上学期期末联考数学试卷(Word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 229.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-31 00:00:00 | ||
图片预览


文档简介
(
学号
座位号
姓名
班级
学校
)上海市虹口区2020-2021学年度第一学期七年级数学期末联考试卷
(测试时间90分钟,满分100分) 2021.1
题号 一 二 三 四 总分
得分
一、单项选择题(本大题共6题,每题2分,满分12分)
1.“与的差的倒数,”用式子表示是 …………………………………………( )
A. B. C. D.
2.下列运算正确的是………………………………………………………………( )
A. B. C. D.
3.要使分式有意义,x的取值应满足 ……………………………………( )
A. B. C. D.
4.如果将分式中的和都扩大到原来的3倍,那么分式的值……( )
A.扩大到原来的3倍; B.扩大到原来的9倍;
C.缩小到原来的; D.不变.
5.下列图形中是旋转对称图形但不是中心对称图形的是……………………( )
6.下列说法正确的是……………………………………………………………( )
A.能够互相重合的两个图形成轴对称
B.图形的平移运动由移动的方向决定
C.如果一个旋转对称图形有一个旋转角为120°,那么它不是中心对称图形
D.如果一个旋转对称图形有一个旋转角为180°,那么它是中心对称图形.
二、填空题(本大题共14题,每题2分,满分28分)
7.单项式的次数是 次.
8.计算: .
9.计算: .
10.因式分解: .
11.计算:÷= .
12.当x= 时,分式的值为0.
13.方程如果有增根,那么增根一定是 .
14.计算: .
15.用科学记数法表示: .
16.将代数式表示成只含有正整数指数幂的形式为 .
17.如图,把纸片沿折叠,使点落在四边形的外部.已知,,则的度数是 度.
18.小杰从镜子中看到电子钟的示数是 ,那么此时实际时间是 .
19.已知大正方形的边长为4厘米,小正方形的边长为2厘米,起始状态如图2所示. 大正方形固定不动,把小正方形向右平移,当两个正方形重叠部分的面积为2平方厘米时,小正方形平移的距离为 厘米.
20.如图,直角三角形ABC中,,将三角形的斜边AB放在定直线L上,将点A按顺时针方向在L上转动两次,转动到的位置,设BC=1,AC=,AB=2,则点A所经过的路线长是 .
三、简答题(本大题共6题,每题6分,满分36分)
21.计算: 22.因式分解:
解: 解:
23.计算:(结果不含负整数指数幂).
解:
24. 计算:
解:
25.解方程:
解:
26.图1、图2均为7×6的正方形网格,点A、B、C在格点上.
(1)在图1中确定格点D,并画出以A、B、C、D为顶点的四边形,使其为轴对称图形. (试画出2个符合要求的点,分别记为D1、D2)
(2)在图2中确定格点E,并画出以A、B、C、E为顶点的四边形,使其为中心对称图形.(试画出2个符合要求的点,分别记为E1、E2)
四、解答题(本大题共3题,每题8分,满分24分)
27.先化简,再求值,其中.
解:
(
学号
座位号
姓名
班级
学校
)28.百果园果品店在批发市场购买某种水果销售,第一次用1200元购进若干千克,由于水果畅销,很快售完,第二次用1452元购买了一批水果,每千克的进价比第一次提高了10%,所购买的水果的数量比第一次多20千克,求第一次购买水果的进价是每千克多少元?
解:
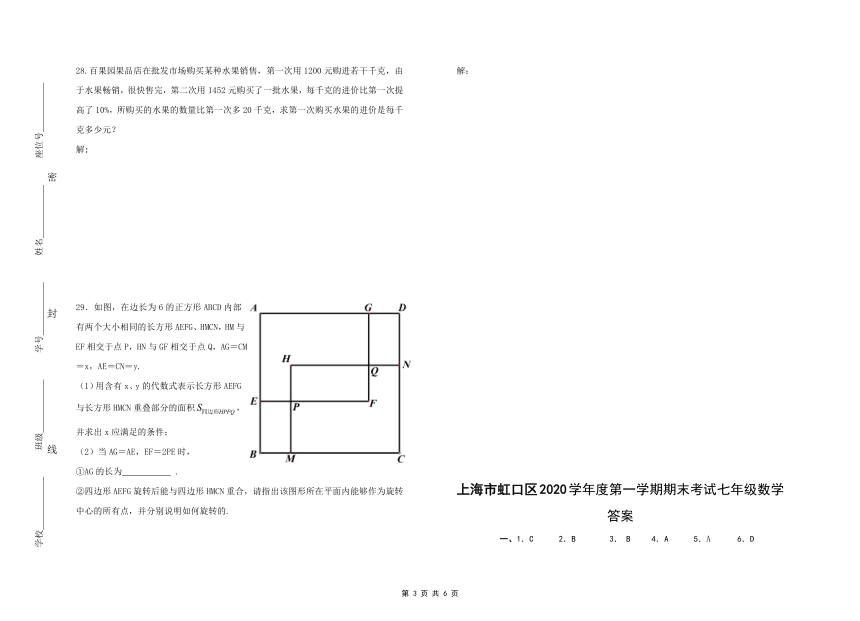
29.如图,在边长为6的正方形ABCD内部有两个大小相同的长方形AEFG、HMCN,HM与EF相交于点P,HN与GF相交于点Q,AG=CM=x,AE=CN=y.
(1)用含有x、y的代数式表示长方形AEFG与长方形HMCN重叠部分的面积,并求出x应满足的条件;
(2)当AG=AE,EF=2PE时,
①AG的长为 .
②四边形AEFG旋转后能与四边形HMCN重合,请指出该图形所在平面内能够作为旋转中心的所有点,并分别说明如何旋转的.
解:
上海市虹口区2020学年度第一学期期末考试七年级数学答案
一、1.C 2.B 3. B 4.A 5.A 6.D
二、7.5 8. 9.10. 11. 12. x=-4
13.X=1 14.2 15.- 16. 17.40 18.21:05 19. 1或5 20.
三、21.计算:
解: 原式=(2分)
= ………(2分)
= …………(2分)
22.因式分解:
解:原式 ……………………(3分)
……………………(3分)
23.计算:(结果不含负整数指数幂).
解:原式=……………………(2分)
……………………(2分)
……………………(1分)
…………………………………………(1分)
24. 解:原式 = ……………………(4分)
= ……………………(1分)
= ……………………(1分)
25.解: ………………………(2分)
………………(1分)
……………(1分)
经检验:是原方程的解 …………(1分)
所以原方程的解为.……… …(1分)
26.
四、解答题:
27.解:原式=-----------(2分)
=----------(2分)
=.---------------------------(2分)
当时,=.-----------(2分)
28.解:(1)解:设第一次购买水果的进价为每千克元,则第二次购买水果的进价为每千克元. (1分)
---------------------------(4分)
--------------------------------------------(1分)
经检验,是原方程的根且符合题意. (1分)
答:第一次购买水果的进价为每千克6元. (1分)
29.解:(1)PM=BE=AB-AE=6-y,那么PH=HM-PM=y-(6-y)=2y-6, ----(1分)
PE=BM=BC-CM=6-x,那么PF=EF-PE=x-(6-x)=2x-6, -------(1分)
=(2x-6)(2y-6)=4xy-12x-12y+36, ----------(1分)
x应满足的条件是:3(2)①当AG=AE,EF=2PE时,求得AG=x=4. ---------(1分)
②四边形AEFG、HMCN都是正方形,点P既是EF的中点也是HM的中点,点Q既是GF的中点也是HN的中点,设HF、PQ的相交于点O.
四边形AEFG绕点O逆时针方向(或顺时针方向)旋转180度可与四边形HMCN重合; ----------(1分)
四边形AEFG绕点P顺时针方向旋转90度(或逆时针方向旋转270度)可与四边形HMCN重合;----------(1分)
四边形AEFG绕点Q逆时针方向旋转90度(或顺时针方向旋转270度)可与四边形HMCN重合;----------(1分)
学号
座位号
姓名
班级
学校
)上海市虹口区2020-2021学年度第一学期七年级数学期末联考试卷
(测试时间90分钟,满分100分) 2021.1
题号 一 二 三 四 总分
得分
一、单项选择题(本大题共6题,每题2分,满分12分)
1.“与的差的倒数,”用式子表示是 …………………………………………( )
A. B. C. D.
2.下列运算正确的是………………………………………………………………( )
A. B. C. D.
3.要使分式有意义,x的取值应满足 ……………………………………( )
A. B. C. D.
4.如果将分式中的和都扩大到原来的3倍,那么分式的值……( )
A.扩大到原来的3倍; B.扩大到原来的9倍;
C.缩小到原来的; D.不变.
5.下列图形中是旋转对称图形但不是中心对称图形的是……………………( )
6.下列说法正确的是……………………………………………………………( )
A.能够互相重合的两个图形成轴对称
B.图形的平移运动由移动的方向决定
C.如果一个旋转对称图形有一个旋转角为120°,那么它不是中心对称图形
D.如果一个旋转对称图形有一个旋转角为180°,那么它是中心对称图形.
二、填空题(本大题共14题,每题2分,满分28分)
7.单项式的次数是 次.
8.计算: .
9.计算: .
10.因式分解: .
11.计算:÷= .
12.当x= 时,分式的值为0.
13.方程如果有增根,那么增根一定是 .
14.计算: .
15.用科学记数法表示: .
16.将代数式表示成只含有正整数指数幂的形式为 .
17.如图,把纸片沿折叠,使点落在四边形的外部.已知,,则的度数是 度.
18.小杰从镜子中看到电子钟的示数是 ,那么此时实际时间是 .
19.已知大正方形的边长为4厘米,小正方形的边长为2厘米,起始状态如图2所示. 大正方形固定不动,把小正方形向右平移,当两个正方形重叠部分的面积为2平方厘米时,小正方形平移的距离为 厘米.
20.如图,直角三角形ABC中,,将三角形的斜边AB放在定直线L上,将点A按顺时针方向在L上转动两次,转动到的位置,设BC=1,AC=,AB=2,则点A所经过的路线长是 .
三、简答题(本大题共6题,每题6分,满分36分)
21.计算: 22.因式分解:
解: 解:
23.计算:(结果不含负整数指数幂).
解:
24. 计算:
解:
25.解方程:
解:
26.图1、图2均为7×6的正方形网格,点A、B、C在格点上.
(1)在图1中确定格点D,并画出以A、B、C、D为顶点的四边形,使其为轴对称图形. (试画出2个符合要求的点,分别记为D1、D2)
(2)在图2中确定格点E,并画出以A、B、C、E为顶点的四边形,使其为中心对称图形.(试画出2个符合要求的点,分别记为E1、E2)
四、解答题(本大题共3题,每题8分,满分24分)
27.先化简,再求值,其中.
解:
(
学号
座位号
姓名
班级
学校
)28.百果园果品店在批发市场购买某种水果销售,第一次用1200元购进若干千克,由于水果畅销,很快售完,第二次用1452元购买了一批水果,每千克的进价比第一次提高了10%,所购买的水果的数量比第一次多20千克,求第一次购买水果的进价是每千克多少元?
解:
29.如图,在边长为6的正方形ABCD内部有两个大小相同的长方形AEFG、HMCN,HM与EF相交于点P,HN与GF相交于点Q,AG=CM=x,AE=CN=y.
(1)用含有x、y的代数式表示长方形AEFG与长方形HMCN重叠部分的面积,并求出x应满足的条件;
(2)当AG=AE,EF=2PE时,
①AG的长为 .
②四边形AEFG旋转后能与四边形HMCN重合,请指出该图形所在平面内能够作为旋转中心的所有点,并分别说明如何旋转的.
解:
上海市虹口区2020学年度第一学期期末考试七年级数学答案
一、1.C 2.B 3. B 4.A 5.A 6.D
二、7.5 8. 9.10. 11. 12. x=-4
13.X=1 14.2 15.- 16. 17.40 18.21:05 19. 1或5 20.
三、21.计算:
解: 原式=(2分)
= ………(2分)
= …………(2分)
22.因式分解:
解:原式 ……………………(3分)
……………………(3分)
23.计算:(结果不含负整数指数幂).
解:原式=……………………(2分)
……………………(2分)
……………………(1分)
…………………………………………(1分)
24. 解:原式 = ……………………(4分)
= ……………………(1分)
= ……………………(1分)
25.解: ………………………(2分)
………………(1分)
……………(1分)
经检验:是原方程的解 …………(1分)
所以原方程的解为.……… …(1分)
26.
四、解答题:
27.解:原式=-----------(2分)
=----------(2分)
=.---------------------------(2分)
当时,=.-----------(2分)
28.解:(1)解:设第一次购买水果的进价为每千克元,则第二次购买水果的进价为每千克元. (1分)
---------------------------(4分)
--------------------------------------------(1分)
经检验,是原方程的根且符合题意. (1分)
答:第一次购买水果的进价为每千克6元. (1分)
29.解:(1)PM=BE=AB-AE=6-y,那么PH=HM-PM=y-(6-y)=2y-6, ----(1分)
PE=BM=BC-CM=6-x,那么PF=EF-PE=x-(6-x)=2x-6, -------(1分)
=(2x-6)(2y-6)=4xy-12x-12y+36, ----------(1分)
x应满足的条件是:3
②四边形AEFG、HMCN都是正方形,点P既是EF的中点也是HM的中点,点Q既是GF的中点也是HN的中点,设HF、PQ的相交于点O.
四边形AEFG绕点O逆时针方向(或顺时针方向)旋转180度可与四边形HMCN重合; ----------(1分)
四边形AEFG绕点P顺时针方向旋转90度(或逆时针方向旋转270度)可与四边形HMCN重合;----------(1分)
四边形AEFG绕点Q逆时针方向旋转90度(或顺时针方向旋转270度)可与四边形HMCN重合;----------(1分)
同课章节目录
