12.2 三角形全等的判定 训练 2021-2022学年人教版数学八年级上册(word版含解析)
文档属性
| 名称 | 12.2 三角形全等的判定 训练 2021-2022学年人教版数学八年级上册(word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 396.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-02 08:51:32 | ||
图片预览


文档简介
人教版数学 八年级上册 12.2 三角形全等的判定 创新训练
一、选择题
1. 如图,已知AB=AD,若利用SSS证明△ABC≌△ADC,则需要添加的条件是( )
A.AC=AC
B.∠B=∠D
C.BC=DC
D.AB=CD
2. 如图所示,某同学把一块三角形的玻璃不小心打碎成了三块,现在要到
玻璃店去配一块完全一样的玻璃,那么最省事的办法是带哪一块去 ( )
A. ① B. ②
C. ③ D. ①和②
3. 如图所示,P是∠BAC内一点,且点P到AB,AC的距离PE,PF相等,则△PEA≌△PFA的依据是( )
A.HL B.ASA C.SSS D.SAS
4. 如图,AB⊥BC,BE⊥AC,垂足分别为B,E,∠1=∠2,AD=AB,则下列结论正确的是( )
A.∠1=∠EFD B.BE=EC C.BF=CD D.FD∥BC
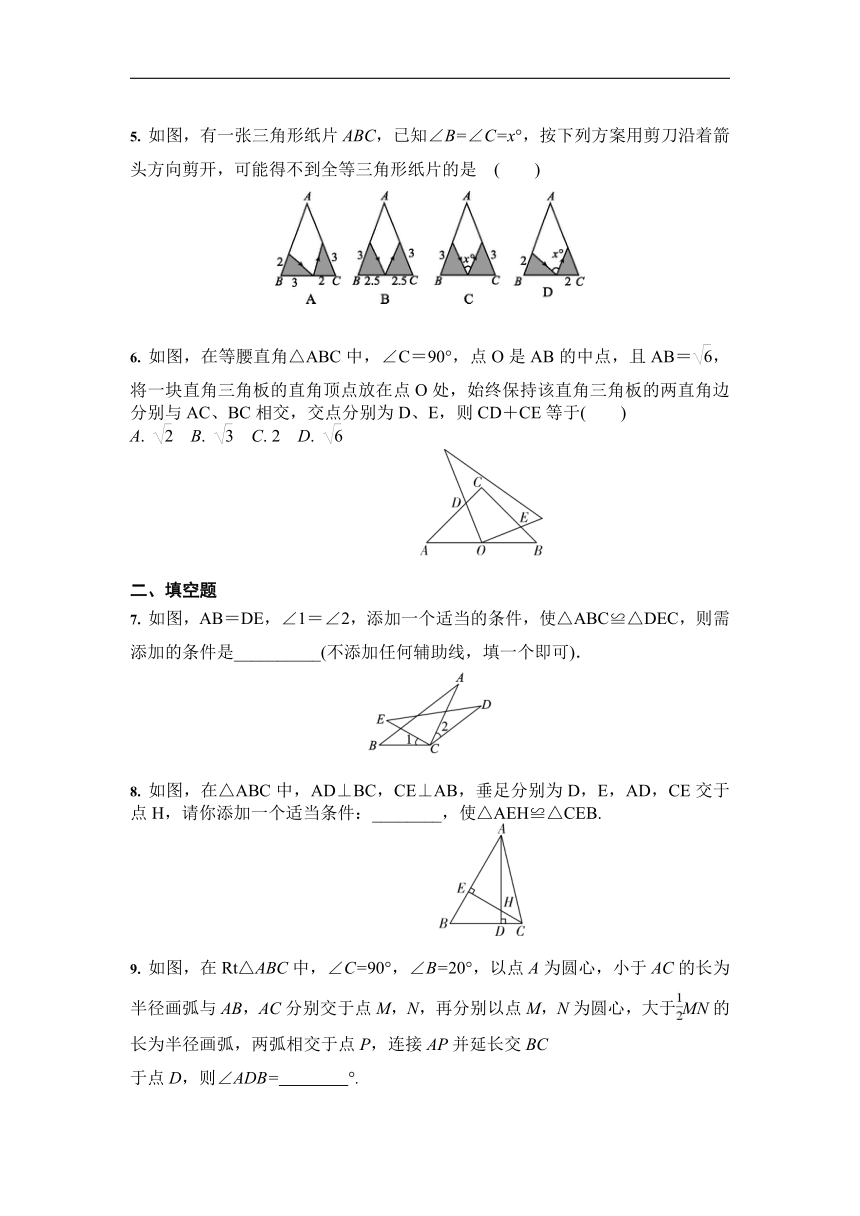
5. 如图,有一张三角形纸片ABC,已知∠B=∠C=x°,按下列方案用剪刀沿着箭头方向剪开,可能得不到全等三角形纸片的是 ( )
6. 如图,在等腰直角△ABC中,∠C=90°,点O是AB的中点,且AB=,将一块直角三角板的直角顶点放在点O处,始终保持该直角三角板的两直角边分别与AC、BC相交,交点分别为D、E,则CD+CE等于( )
A. B. C. 2 D.
二、填空题
7. 如图,AB=DE,∠1=∠2,添加一个适当的条件,使△ABC≌△DEC,则需添加的条件是__________(不添加任何辅助线,填一个即可).
8. 如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D,E,AD,CE交于点H,请你添加一个适当条件:________,使△AEH≌△CEB.
9. 如图,在Rt△ABC中,∠C=90°,∠B=20°,以点A为圆心,小于AC的长为半径画弧与AB,AC分别交于点M,N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧相交于点P,连接AP并延长交BC
于点D,则∠ADB= °.
10. 如图,已知CD=CA,∠1=∠2,要使△ECD≌△BCA,需添加的条件是__________(只需写出一个条件).
11. 如图,在△ABC中,D,E分别是边AB,AC上的点,过点C作平行于AB的直线交DE的延长线于点F.若DE=FE,AB=5,CF=3,则BD的长是________.
12. 在平面直角坐标系xOy中,已知点A,B的坐标分别为(2,0),(2,4),若以A,B,P为顶点的三角形与△ABO全等,则点P的坐标为________________________.
13. 如图,在Rt△ABC中,∠ACB=90°,BC=2 cm,CD⊥AB,在AC上取一点E,使EC=BC,过点E作EF⊥AC交CD的延长线于点F.若EF=5 cm,则AE=________cm.
14. 如图,∠C=90°,AC=10,BC=5,AX⊥AC,点P和点Q是线段AC与射线AX上的两个动点,且AB=PQ,当AP=________时,△ABC与△APQ全等.
三、解答题
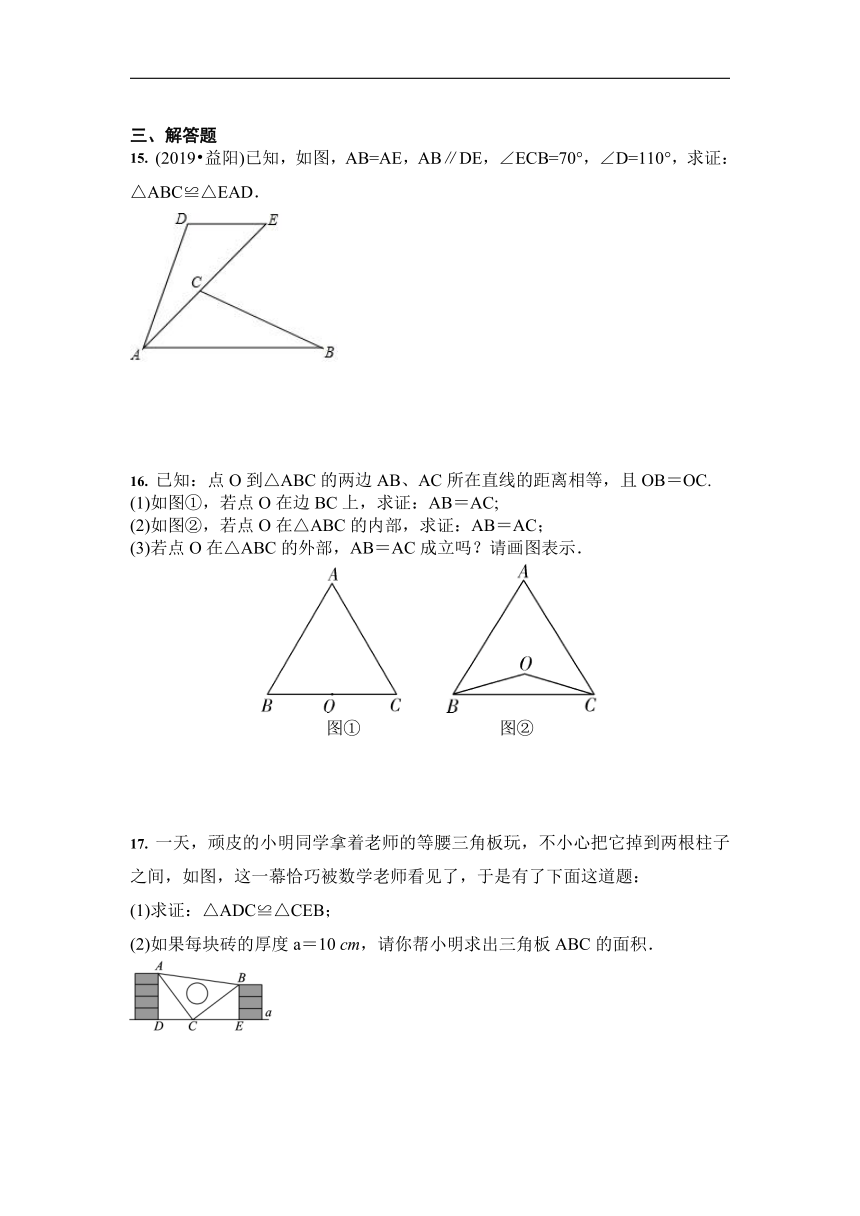
15. (2019 益阳)已知,如图,AB=AE,AB∥DE,∠ECB=70°,∠D=110°,求证:△ABC≌△EAD.
16. 已知:点O到△ABC的两边AB、AC所在直线的距离相等,且OB=OC.
(1)如图①,若点O在边BC上,求证:AB=AC;
(2)如图②,若点O在△ABC的内部,求证:AB=AC;
(3)若点O在△ABC的外部,AB=AC成立吗?请画图表示.
图① 图②
17. 一天,顽皮的小明同学拿着老师的等腰三角板玩,不小心把它掉到两根柱子之间,如图,这一幕恰巧被数学老师看见了,于是有了下面这道题:
(1)求证:△ADC≌△CEB;
(2)如果每块砖的厚度a=10 cm,请你帮小明求出三角板ABC的面积.
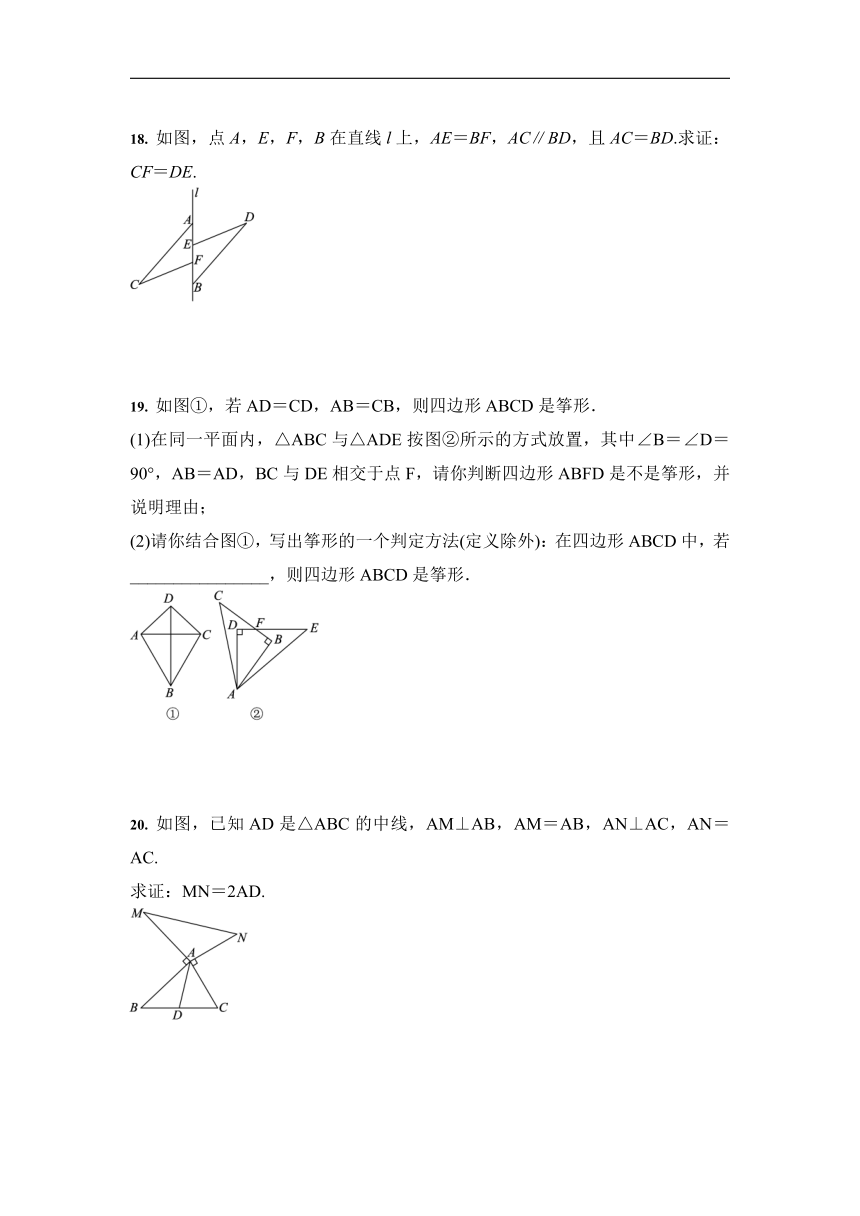
18. 如图,点A,E,F,B在直线l上,AE=BF,AC∥BD,且AC=BD.求证:CF=DE.
19. 如图①,若AD=CD,AB=CB,则四边形ABCD是筝形.
(1)在同一平面内,△ABC与△ADE按图②所示的方式放置,其中∠B=∠D=90°,AB=AD,BC与DE相交于点F,请你判断四边形ABFD是不是筝形,并说明理由;
(2)请你结合图①,写出筝形的一个判定方法(定义除外):在四边形ABCD中,若________________,则四边形ABCD是筝形.
20. 如图,已知AD是△ABC的中线,AM⊥AB,AM=AB,AN⊥AC,AN=AC.
求证:MN=2AD.
人教版数学 八年级上册 12.2 三角形全等的判定 创新训练-答案
一、选择题
1. 【答案】C
2. 【答案】 C
3. 【答案】A
4. 【答案】D [解析] 在△AFD和△AFB中,
∴△AFD≌△AFB.
∴∠ADF=∠ABF.
∵AB⊥BC,BE⊥AC,
∴∠BEC=∠ABC=90°.
∴∠ABF+∠EBC=90°,∠C+∠EBC=90°.
∴∠ADF=∠ABF=∠C.
∴FD∥BC.
5. 【答案】C [解析] 选项A中由全等三角形的判定定理“SAS”证得图中两个小三角形全等.
选项B中由全等三角形的判定定理“SAS”证得图中两个小三角形全等.
选项C中,如图①,∵∠DEC=∠B+∠BDE,
∴x°+∠FEC=x°+∠BDE.
∴∠FEC=∠BDE.
这两个角所对的边是BE和CF,而已知条件给的是BD=CF=3,故不能判定两个小三角形全等.
选项D中,如图②,∵∠DEC=∠B+∠BDE,∴x°+∠FEC=x°+∠BDE.
∴∠FEC=∠BDE.
又∵BD=CE=2,∠B=∠C,
∴△BDE≌△CEF.
故能判定两个小三角形全等.
6. 【答案】B 【解析】如解图,连接OC,由已知条件易得∠A=∠OCE,CO=AO,∠DOE=∠COA,∴∠DOE-∠COD=∠COA-∠COD,即∠AOD=∠COE,∴△AOD≌△COE(ASA),∴AD=CE,进而得CD+CE=CD+AD=AC=AB=,故选B.
二、填空题
7. 【答案】答案不唯一,如∠B=∠E
8. 【答案】AH=CB(符合要求即可) 【解析】∵AD⊥BC,CE⊥AB,垂足分别为点D、E,∴∠BEC=∠AEC=90°,在Rt△AEH中,∠EAH=90°-∠AHE,在Rt△HDC中,∠ECB=90°-∠DHC,∵∠AHE=∠DHC,∴∠EAH=∠ECB,∴根据AAS添加AH=CB或EH=EB;根据ASA添加AE=CE.可证△AEH≌△CEB.故答案为:AH=CB或EH=EB或AE=CE均可.
9. 【答案】125 [解析] 由题意可得AD平分∠CAB.∵∠C=90°,∠B=20°,∴∠CAB=70°.
∴∠CAD=∠BAD=35°.∴∠ADB=180°-20°-35°=125°.
10. 【答案】答案不唯一,如CE=CB [解析] 由∠1=∠2,可得∠DCE=∠ACB,又∵CD=CA,∴添加CE=CB,可根据“SAS”判定两个三角形全等.
11. 【答案】2 [解析] ∵CF∥AB,∴∠A=∠FCE.
在△ADE和△CFE中,
∴△ADE≌△CFE(AAS).
∴AD=CF=3.
∴BD=AB-AD=5-3=2.
12. 【答案】(4,0)或(4,4)或(0,4)
13. 【答案】3 [解析] ∵∠ACB=90°,∴∠ECF+∠BCD=90°.∵CD⊥AB,∴∠BCD+∠B=90°.
∴∠ECF=∠B.
在△ABC和△FCE中,
∴△ABC≌△FCE(ASA).∴AC=FE.
∵AE=AC-CE,BC=2 cm,EF=5 cm,
∴AE=5-2=3(cm).
14. 【答案】5或10 [解析] ∵AX⊥AC,∴∠PAQ=90°.∴∠C=∠PAQ=90°.
分两种情况:①当AP=BC=5时,
在Rt△ABC和Rt△QPA中,
∴Rt△ABC≌Rt△QPA(HL);
②当AP=CA=10时,
在Rt△ABC和Rt△PQA中,
∴Rt△ABC≌Rt△PQA(HL).
综上所述,当AP=5或10时,△ABC与△APQ全等.
三、解答题
15. 【答案】
由∠ECB=70°得∠ACB=110°,
又∵∠D=110°,∴∠ACB=∠D,
∵AB∥DE,
∴∠CAB=∠E,
∴在△ABC和△EAD中,,
∴△ABC≌△EAD.
16. 【答案】
(1)证明:如图①,过点O分别作OE⊥AB,OF⊥AC,E、F分别是垂足,由题意知,OE=OF,OB=OC,
解图①
∴Rt△OEB≌Rt△OFC,
∴∠B=∠C,从而AB=AC.
(2)证明:如图②,过点O分别作OE⊥AB,OF⊥AC,E、F分别是垂足,由题意知,OE=OF.
在Rt△OEB和Rt△OFC中,
∵OE=OF,OB=OC,
解图②
∴Rt△OEB≌Rt△OFC.
∴∠OBE=∠OCF,
又由OB=OC知∠OBC=∠OCB,
∴∠ABC=∠ACB.
∴AB=AC.
(3)解:不一定成立.
(注:当∠A的平分线所在直线与边BC的垂直平分线重合时,有AB=AC;否则,AB≠AC,如示例图③)
解图③
17. 【答案】
解:(1)证明:由题意得AC=CB,∠ACB=90°,AD⊥DE,BE⊥DE,∴∠ADC=∠CEB=90°.
∴∠ACD+∠BCE=90°,∠ACD+∠CAD=90°.∴∠BCE=∠CAD.
在△ADC和△CEB中,
∴△ADC≌△CEB(AAS).
(2)由(1)知△ADC≌△CEB,
∴AD=CE=4a=40 cm,CD=BE=3a=30 cm.
∴DE=70 cm.
∴S△ABC=×(30+40)×70-2××30×40=1250(cm2).
答:三角板ABC的面积为1250 cm2.
18. 【答案】
证明:∵AE=BF,∴AE+EF=BF+EF,
即AF=BE.
∵AC∥BD,∴∠CAF=∠DBE.
在△ACF和△BDE中,
∴△ACF≌△BDE(SAS).
∴CF=DE.
19. 【答案】
解:(1)四边形ABFD是筝形.
理由:连接AF.
在Rt△AFB和Rt△AFD中,
∴Rt△AFB≌Rt△AFD(HL).∴BF=DF.
又∵AB=AD,∴四边形ABFD是筝形.
(2)答案不唯一,如AD=CD,∠ADB=∠CDB
20. 【答案】
证明:如图,延长AD至点E,使DE=AD,连接BE.
∵AD是△ABC的中线,
∴BD=CD.
在△BDE和△CDA中,
∴△BDE≌△CDA(SAS).
∴BE=AC=AN,∠DBE=∠DCA.
∴AC∥BE.∴∠ABE+∠BAC=180°.
∵∠BAM=∠CAN=90°,
∴∠MAN+∠BAC=180°.
∴∠ABE=∠MAN.
在△ABE和△MAN中,
∴△ABE≌△MAN(SAS).
∴AE=MN.
∵AE=2AD,∴MN=2AD.
一、选择题
1. 如图,已知AB=AD,若利用SSS证明△ABC≌△ADC,则需要添加的条件是( )
A.AC=AC
B.∠B=∠D
C.BC=DC
D.AB=CD
2. 如图所示,某同学把一块三角形的玻璃不小心打碎成了三块,现在要到
玻璃店去配一块完全一样的玻璃,那么最省事的办法是带哪一块去 ( )
A. ① B. ②
C. ③ D. ①和②
3. 如图所示,P是∠BAC内一点,且点P到AB,AC的距离PE,PF相等,则△PEA≌△PFA的依据是( )
A.HL B.ASA C.SSS D.SAS
4. 如图,AB⊥BC,BE⊥AC,垂足分别为B,E,∠1=∠2,AD=AB,则下列结论正确的是( )
A.∠1=∠EFD B.BE=EC C.BF=CD D.FD∥BC
5. 如图,有一张三角形纸片ABC,已知∠B=∠C=x°,按下列方案用剪刀沿着箭头方向剪开,可能得不到全等三角形纸片的是 ( )
6. 如图,在等腰直角△ABC中,∠C=90°,点O是AB的中点,且AB=,将一块直角三角板的直角顶点放在点O处,始终保持该直角三角板的两直角边分别与AC、BC相交,交点分别为D、E,则CD+CE等于( )
A. B. C. 2 D.
二、填空题
7. 如图,AB=DE,∠1=∠2,添加一个适当的条件,使△ABC≌△DEC,则需添加的条件是__________(不添加任何辅助线,填一个即可).
8. 如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D,E,AD,CE交于点H,请你添加一个适当条件:________,使△AEH≌△CEB.
9. 如图,在Rt△ABC中,∠C=90°,∠B=20°,以点A为圆心,小于AC的长为半径画弧与AB,AC分别交于点M,N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧相交于点P,连接AP并延长交BC
于点D,则∠ADB= °.
10. 如图,已知CD=CA,∠1=∠2,要使△ECD≌△BCA,需添加的条件是__________(只需写出一个条件).
11. 如图,在△ABC中,D,E分别是边AB,AC上的点,过点C作平行于AB的直线交DE的延长线于点F.若DE=FE,AB=5,CF=3,则BD的长是________.
12. 在平面直角坐标系xOy中,已知点A,B的坐标分别为(2,0),(2,4),若以A,B,P为顶点的三角形与△ABO全等,则点P的坐标为________________________.
13. 如图,在Rt△ABC中,∠ACB=90°,BC=2 cm,CD⊥AB,在AC上取一点E,使EC=BC,过点E作EF⊥AC交CD的延长线于点F.若EF=5 cm,则AE=________cm.
14. 如图,∠C=90°,AC=10,BC=5,AX⊥AC,点P和点Q是线段AC与射线AX上的两个动点,且AB=PQ,当AP=________时,△ABC与△APQ全等.
三、解答题
15. (2019 益阳)已知,如图,AB=AE,AB∥DE,∠ECB=70°,∠D=110°,求证:△ABC≌△EAD.
16. 已知:点O到△ABC的两边AB、AC所在直线的距离相等,且OB=OC.
(1)如图①,若点O在边BC上,求证:AB=AC;
(2)如图②,若点O在△ABC的内部,求证:AB=AC;
(3)若点O在△ABC的外部,AB=AC成立吗?请画图表示.
图① 图②
17. 一天,顽皮的小明同学拿着老师的等腰三角板玩,不小心把它掉到两根柱子之间,如图,这一幕恰巧被数学老师看见了,于是有了下面这道题:
(1)求证:△ADC≌△CEB;
(2)如果每块砖的厚度a=10 cm,请你帮小明求出三角板ABC的面积.
18. 如图,点A,E,F,B在直线l上,AE=BF,AC∥BD,且AC=BD.求证:CF=DE.
19. 如图①,若AD=CD,AB=CB,则四边形ABCD是筝形.
(1)在同一平面内,△ABC与△ADE按图②所示的方式放置,其中∠B=∠D=90°,AB=AD,BC与DE相交于点F,请你判断四边形ABFD是不是筝形,并说明理由;
(2)请你结合图①,写出筝形的一个判定方法(定义除外):在四边形ABCD中,若________________,则四边形ABCD是筝形.
20. 如图,已知AD是△ABC的中线,AM⊥AB,AM=AB,AN⊥AC,AN=AC.
求证:MN=2AD.
人教版数学 八年级上册 12.2 三角形全等的判定 创新训练-答案
一、选择题
1. 【答案】C
2. 【答案】 C
3. 【答案】A
4. 【答案】D [解析] 在△AFD和△AFB中,
∴△AFD≌△AFB.
∴∠ADF=∠ABF.
∵AB⊥BC,BE⊥AC,
∴∠BEC=∠ABC=90°.
∴∠ABF+∠EBC=90°,∠C+∠EBC=90°.
∴∠ADF=∠ABF=∠C.
∴FD∥BC.
5. 【答案】C [解析] 选项A中由全等三角形的判定定理“SAS”证得图中两个小三角形全等.
选项B中由全等三角形的判定定理“SAS”证得图中两个小三角形全等.
选项C中,如图①,∵∠DEC=∠B+∠BDE,
∴x°+∠FEC=x°+∠BDE.
∴∠FEC=∠BDE.
这两个角所对的边是BE和CF,而已知条件给的是BD=CF=3,故不能判定两个小三角形全等.
选项D中,如图②,∵∠DEC=∠B+∠BDE,∴x°+∠FEC=x°+∠BDE.
∴∠FEC=∠BDE.
又∵BD=CE=2,∠B=∠C,
∴△BDE≌△CEF.
故能判定两个小三角形全等.
6. 【答案】B 【解析】如解图,连接OC,由已知条件易得∠A=∠OCE,CO=AO,∠DOE=∠COA,∴∠DOE-∠COD=∠COA-∠COD,即∠AOD=∠COE,∴△AOD≌△COE(ASA),∴AD=CE,进而得CD+CE=CD+AD=AC=AB=,故选B.
二、填空题
7. 【答案】答案不唯一,如∠B=∠E
8. 【答案】AH=CB(符合要求即可) 【解析】∵AD⊥BC,CE⊥AB,垂足分别为点D、E,∴∠BEC=∠AEC=90°,在Rt△AEH中,∠EAH=90°-∠AHE,在Rt△HDC中,∠ECB=90°-∠DHC,∵∠AHE=∠DHC,∴∠EAH=∠ECB,∴根据AAS添加AH=CB或EH=EB;根据ASA添加AE=CE.可证△AEH≌△CEB.故答案为:AH=CB或EH=EB或AE=CE均可.
9. 【答案】125 [解析] 由题意可得AD平分∠CAB.∵∠C=90°,∠B=20°,∴∠CAB=70°.
∴∠CAD=∠BAD=35°.∴∠ADB=180°-20°-35°=125°.
10. 【答案】答案不唯一,如CE=CB [解析] 由∠1=∠2,可得∠DCE=∠ACB,又∵CD=CA,∴添加CE=CB,可根据“SAS”判定两个三角形全等.
11. 【答案】2 [解析] ∵CF∥AB,∴∠A=∠FCE.
在△ADE和△CFE中,
∴△ADE≌△CFE(AAS).
∴AD=CF=3.
∴BD=AB-AD=5-3=2.
12. 【答案】(4,0)或(4,4)或(0,4)
13. 【答案】3 [解析] ∵∠ACB=90°,∴∠ECF+∠BCD=90°.∵CD⊥AB,∴∠BCD+∠B=90°.
∴∠ECF=∠B.
在△ABC和△FCE中,
∴△ABC≌△FCE(ASA).∴AC=FE.
∵AE=AC-CE,BC=2 cm,EF=5 cm,
∴AE=5-2=3(cm).
14. 【答案】5或10 [解析] ∵AX⊥AC,∴∠PAQ=90°.∴∠C=∠PAQ=90°.
分两种情况:①当AP=BC=5时,
在Rt△ABC和Rt△QPA中,
∴Rt△ABC≌Rt△QPA(HL);
②当AP=CA=10时,
在Rt△ABC和Rt△PQA中,
∴Rt△ABC≌Rt△PQA(HL).
综上所述,当AP=5或10时,△ABC与△APQ全等.
三、解答题
15. 【答案】
由∠ECB=70°得∠ACB=110°,
又∵∠D=110°,∴∠ACB=∠D,
∵AB∥DE,
∴∠CAB=∠E,
∴在△ABC和△EAD中,,
∴△ABC≌△EAD.
16. 【答案】
(1)证明:如图①,过点O分别作OE⊥AB,OF⊥AC,E、F分别是垂足,由题意知,OE=OF,OB=OC,
解图①
∴Rt△OEB≌Rt△OFC,
∴∠B=∠C,从而AB=AC.
(2)证明:如图②,过点O分别作OE⊥AB,OF⊥AC,E、F分别是垂足,由题意知,OE=OF.
在Rt△OEB和Rt△OFC中,
∵OE=OF,OB=OC,
解图②
∴Rt△OEB≌Rt△OFC.
∴∠OBE=∠OCF,
又由OB=OC知∠OBC=∠OCB,
∴∠ABC=∠ACB.
∴AB=AC.
(3)解:不一定成立.
(注:当∠A的平分线所在直线与边BC的垂直平分线重合时,有AB=AC;否则,AB≠AC,如示例图③)
解图③
17. 【答案】
解:(1)证明:由题意得AC=CB,∠ACB=90°,AD⊥DE,BE⊥DE,∴∠ADC=∠CEB=90°.
∴∠ACD+∠BCE=90°,∠ACD+∠CAD=90°.∴∠BCE=∠CAD.
在△ADC和△CEB中,
∴△ADC≌△CEB(AAS).
(2)由(1)知△ADC≌△CEB,
∴AD=CE=4a=40 cm,CD=BE=3a=30 cm.
∴DE=70 cm.
∴S△ABC=×(30+40)×70-2××30×40=1250(cm2).
答:三角板ABC的面积为1250 cm2.
18. 【答案】
证明:∵AE=BF,∴AE+EF=BF+EF,
即AF=BE.
∵AC∥BD,∴∠CAF=∠DBE.
在△ACF和△BDE中,
∴△ACF≌△BDE(SAS).
∴CF=DE.
19. 【答案】
解:(1)四边形ABFD是筝形.
理由:连接AF.
在Rt△AFB和Rt△AFD中,
∴Rt△AFB≌Rt△AFD(HL).∴BF=DF.
又∵AB=AD,∴四边形ABFD是筝形.
(2)答案不唯一,如AD=CD,∠ADB=∠CDB
20. 【答案】
证明:如图,延长AD至点E,使DE=AD,连接BE.
∵AD是△ABC的中线,
∴BD=CD.
在△BDE和△CDA中,
∴△BDE≌△CDA(SAS).
∴BE=AC=AN,∠DBE=∠DCA.
∴AC∥BE.∴∠ABE+∠BAC=180°.
∵∠BAM=∠CAN=90°,
∴∠MAN+∠BAC=180°.
∴∠ABE=∠MAN.
在△ABE和△MAN中,
∴△ABE≌△MAN(SAS).
∴AE=MN.
∵AE=2AD,∴MN=2AD.
