13.3 等腰三角形 创新训练 2021-2022学年人教版数学 八年级上册(word版含答案)
文档属性
| 名称 | 13.3 等腰三角形 创新训练 2021-2022学年人教版数学 八年级上册(word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 529.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-02 08:59:19 | ||
图片预览



文档简介
人教版数学 八年级上册 13.3 等腰三角形 创新训练
一、选择题
1. 如图,在△ABC中,AB=AC,AD,CE分别是△ABC的中线和角平分线.若∠CAD=20°,则∠ACE的度数是( )
A.20° B.35° C.40° D.70°
2. 在△ABC中,与∠A相邻的外角是110°,要使△ABC为等腰三角形,则∠B的度数是( )
A.70° B.55°
C.70°或55° D.70°或55°或40°
3. 如图,以点O为圆心,任意长为半径画弧,与射线OM交于点A,再以点A为圆心,AO长为半径画弧,两弧交于点B,画出射线OB,则∠AOB等于( )
A.30° B.45° C.60° D.90°
4. 如图,下列条件不能推出△ABC是等腰三角形的是( )
A.∠B=∠C B.AD⊥BC,∠BAD=∠CAD
C.AD⊥BC,BD=CD D.AD⊥BC,∠BAD=∠ACD
5. 如图,在△ABC中,∠ABC的平分线交AC于点D,AD=6,过点D作DE∥BC交AB于点E.若△AED的周长为16,则边AB的长为( )
A.6 B.8 C.10 D.12
6. 如图,△ABC是等边三角形,DE∥BC.若AB=10,BD=6,则△ADE的周长为( )
A.4 B.12 C.18 D.30
7. (2020·天门仙桃潜江)如图,已知△ABC和△ADE都是等腰三角形,∠BAC∠DAE90°,BD,CE交于点F,连接AF.下列结论:①BDCE;②BF⊥CF;③AF平分∠CAD;④∠AFE45°.其中正确结论的个数有
A.1 B.2个 C.3个 D.4个
8. (2020·宜宾)如图,△ABC和△ECD都是等边三角形,且点B、C、D在一条直线上,连结BE、AD,点M、N分别是线段BE、AD上的两点,且BM=BE,AN=AD,则△CMN的形状是( )
A.等腰三角形 B.直角三角形 C.等边三角形 D.不等边三角形
二、填空题
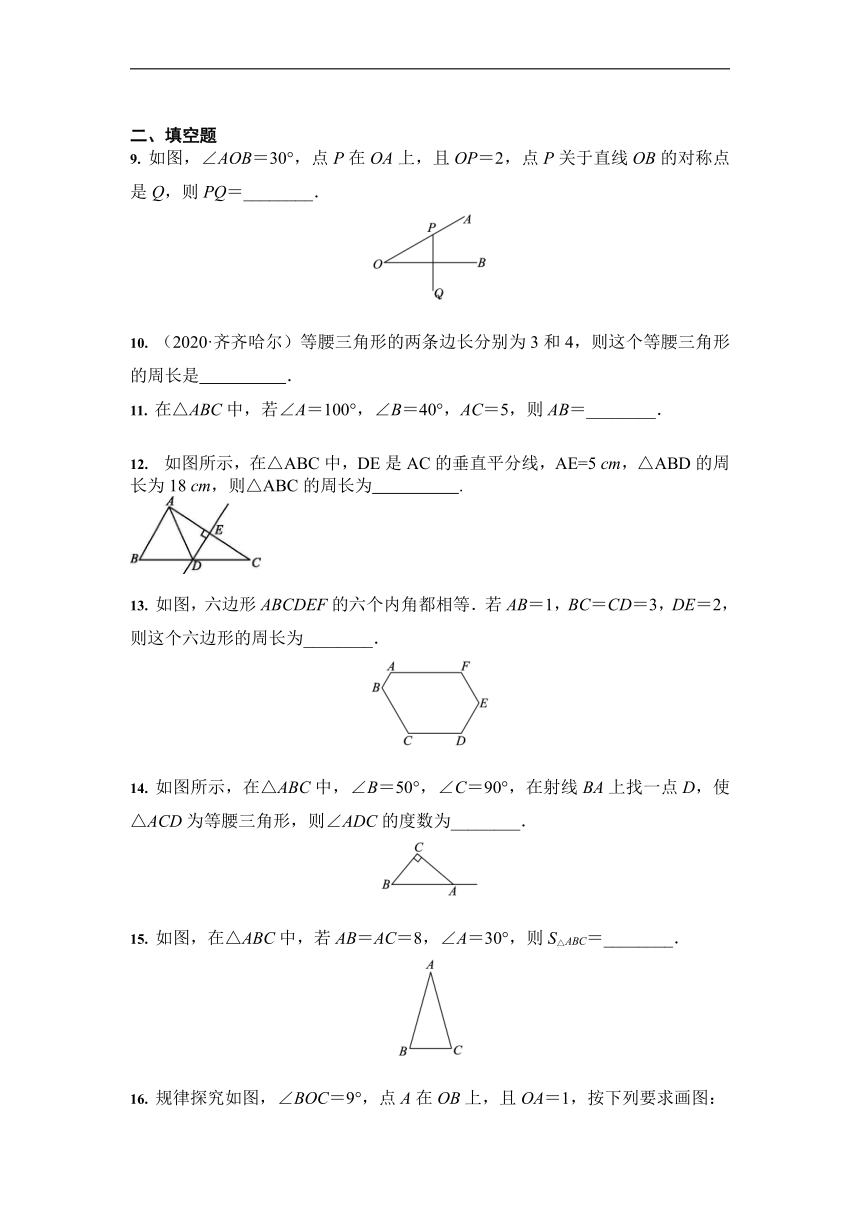
9. 如图,∠AOB=30°,点P在OA上,且OP=2,点P关于直线OB的对称点是Q,则PQ=________.
10. (2020·齐齐哈尔)等腰三角形的两条边长分别为3和4,则这个等腰三角形的周长是 .
11. 在△ABC中,若∠A=100°,∠B=40°,AC=5,则AB=________.
12. 如图所示,在△ABC中,DE是AC的垂直平分线,AE=5 cm,△ABD的周长为18 cm,则△ABC的周长为 .
13. 如图,六边形ABCDEF的六个内角都相等.若AB=1,BC=CD=3,DE=2,则这个六边形的周长为________.
14. 如图所示,在△ABC中,∠B=50°,∠C=90°,在射线BA上找一点D,使△ACD为等腰三角形,则∠ADC的度数为________.
15. 如图,在△ABC中,若AB=AC=8,∠A=30°,则S△ABC=________.
16. 规律探究如图,∠BOC=9°,点A在OB上,且OA=1,按下列要求画图:
以A为圆心,1为半径向右画弧交OC于点A1,得第1条线段AA1;
再以A1为圆心,1为半径向右画弧交OB于点A2,得第2条线段A1A2;
再以A2为圆心,1为半径向右画弧交OC于点A3,得第3条线段A2A3……
这样画下去,直到得第n条线段,之后就不能再画出符合要求的线段了,则n=________.
三、解答题
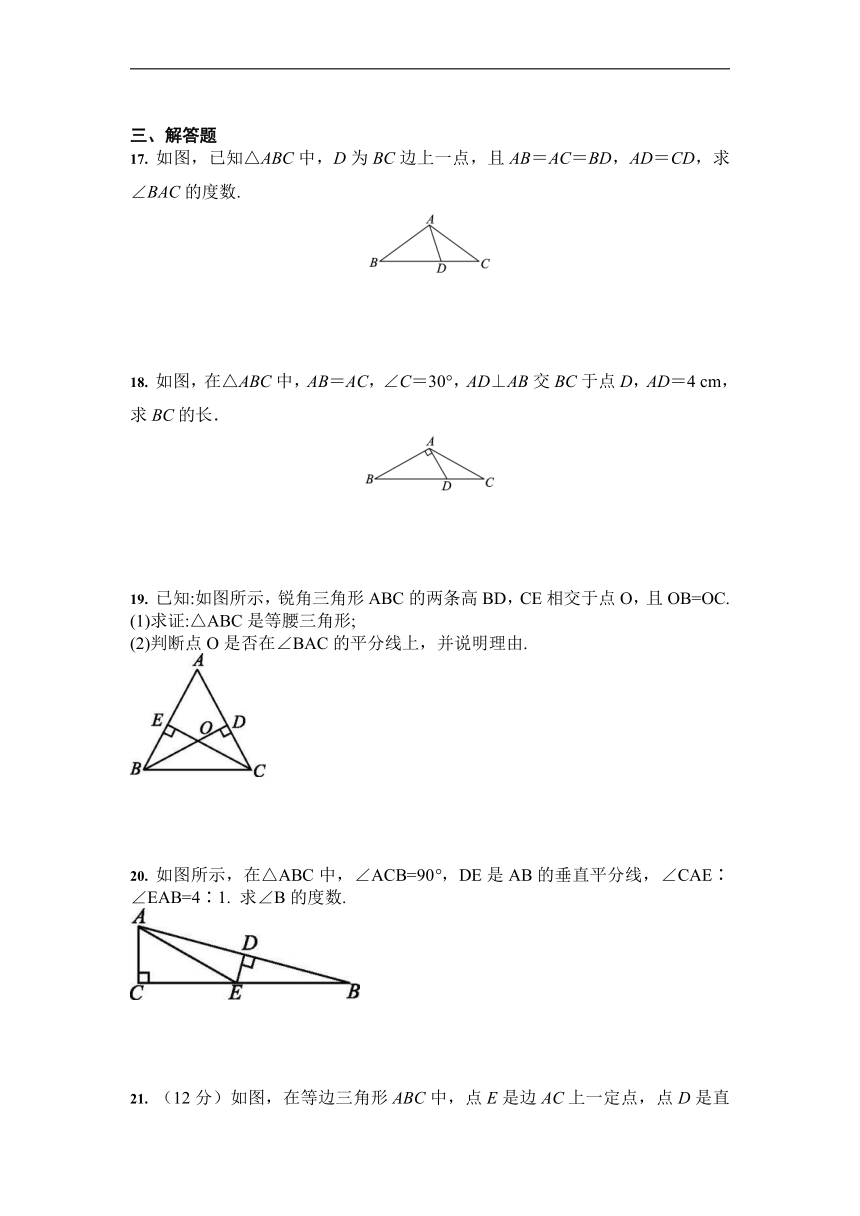
17. 如图,已知△ABC中,D为BC边上一点,且AB=AC=BD,AD=CD,求∠BAC的度数.
18. 如图,在△ABC中,AB=AC,∠C=30°,AD⊥AB交BC于点D,AD=4 cm,求BC的长.
19. 已知:如图所示,锐角三角形ABC的两条高BD,CE相交于点O,且OB=OC.
(1)求证:△ABC是等腰三角形;
(2)判断点O是否在∠BAC的平分线上,并说明理由.
20. 如图所示,在△ABC中,∠ACB=90°,DE是AB的垂直平分线,∠CAE∶∠EAB=4∶1. 求∠B的度数.
21. (12分)如图,在等边三角形ABC中,点E是边AC上一定点,点D是直线BC上一动点,以DE为一边作等边三角形DEF,连接CF.
【问题解决】
如图1,若点D在边BC上,求证:CE+CF=CD;
【类比探究】
如图2,若点D在边BC的延长线上,请探究线段CE,CF与CD之间存在怎样的数量关系?并说明理由.
人教版数学 八年级上册 13.3 等腰三角形 创新训练-答案
一、选择题
1. 【答案】B
2. 【答案】D [解析] 由题意得,∠A=70°,当∠B=∠A=70°时,△ABC为等腰三角形;
当∠B=55°时,可得∠C=55°,∠B=∠C,△ABC为等腰三角形;
当∠B=40°时,可得∠C=70°=∠A,△ABC为等腰三角形.
3. 【答案】C [解析] 连接AB.根据题意得 OB=OA=AB,∴△AOB是等边三角形.∴∠AOB=60°.
4. 【答案】D [解析] 选项A由等角对等边可得△ABC是等腰三角形;选项B由所给条件可得△ADB≌△ADC,由全等三角形的性质可得AB=AC;选项C由垂直平分线的性质可得AB=AC;选项D不可以得到AB=AC.
5. 【答案】C [解析] ∵BD平分∠ABC,
∴∠EBD=∠CBD.
∵DE∥BC,∴∠EDB=∠CBD.
∴∠EBD=∠EDB.∴BE=DE.
∵△AED的周长为16,
∴AE+DE+AD=AE+BE+AD=AB+AD=16.
∵AD=6,∴AB=10.
6. 【答案】B [解析] ∵△ABC为等边三角形,∴∠A=∠B=∠C=60°.∵DE∥BC,∴∠ADE=∠B=60°,∠AED=∠C=60°.∴△ADE为等边三角形.∵AB=10,BD=6,∴AD=AB-BD=10-6=4.∴△ADE的周长为4×3=12.
7. 【答案】C
【解析】∵△ABC和△ADE都是等腰直角三角形,
∴AB=AC,AD=AE,
∵∠BAD=90°+∠CAD,
∠CAE=90°+∠CAD,
∴∠BAD=∠CAE,
在△AEC与△ADB中,
,
∴△AEC≌△ADB(SAS),
∴BD=CE,故①正确;
∴∠ADB=∠AEC,
∵∠DEF+∠AEC+∠EDA=90°,
∴∠DEF+∠ADB+∠EDA=90°
∴∠DEF+∠EDF=90 ,
∴BD⊥CE,故②正确;
∵作AN⊥CE,AM⊥BD
∵△AEC≌△ADB(SAS),
∴AM=AN,
∵AF是∠BFE的角平分线,
∠BFE=90°,
∴∠AFE=45°,故④正确
,故③正确;
因为QF≠PF,故③错误。
正确的有3个,
故选:C.
8. 【答案】 C
【解析】 由△ABC和△ECD都是等边三角形,可得△BCE≌△ACD(SAS),∴∠MBC=∠NAC,BE=AD,∵BM=BE,AN=AD,∴BM=AN,∴△MBC≌△NAC(SAS),∴MC=NC,∠BCM=∠ACN,∵∠BCM+∠MCA=60°,∴∠NCA+∠MCA=60°,∴∠MCN=60°,∴△MCN是等边三角形.
二、填空题
9. 【答案】2 [解析] 如图,连接OQ.
∵点P关于直线OB的对称点是Q,
∴OB垂直平分PQ.
∴∠POB=∠QOB=30°,OP=OQ.∴∠POQ=60°.
∴△POQ为等边三角形.∴PQ=OP=2.
10. 【答案】10或11.
【解析】分3是腰长与底边长两种情况讨论求解即可.①3是腰长时,三角形的三边分别为3、3、4,
∵此时能组成三角形,∴周长=3+3+4=10;
②3是底边长时,三角形的三边分别为3、4、4,此时能组成三角形,所以周长=3+4+4=11.
综上所述,这个等腰三角形的周长是10或11.
故答案为:10或11.
11. 【答案】5
12. 【答案】 28 cm
13. 【答案】15 [解析] 由多边形的内角和定理可知,这个六边形的每个内角都是120°,因此直线AB,CD,EF围成一个等边三角形,且这个等边三角形的边长为7.因此AF=4,EF=2.所以这个六边形的周长=1+3+3+2+2+4=15.
14. 【答案】20°或70°或100° [解析] 如图,有三种情形:
①当AC=AD时,∠ADC=70°;
②当CD′=AD′时,∠AD′C=100°;
③当AC=AD″时,∠AD″C=20°.
15. 【答案】16 [解析] 如图,过点C作CD⊥AB,垂足为D,
则△ADC是含30°角的直角三角形,那么DC=AC=4,∴S△ABC=AB·DC=×8×4=16.
16. 【答案】9
三、解答题
17. 【答案】
解:∵AD=CD,∴设∠DAC=∠C=x°.
∵AB=AC=BD,
∴∠BAD=∠BDA=∠DAC+∠C=2x°,
∠B=∠C=x°.∴∠BAC=3x°.
∵∠B+∠BAC+∠C=180°,∴5x=180,
解得x=36.
∴∠BAC=3x°=108°.
18. 【答案】
解:∵AB=AC,∠C=30°,∴∠B=30°.
∵AB⊥AD,AD=4 cm,∴BD=8 cm.
∵∠ADB=90°-∠B=60°,∠C=30°,
∴∠DAC=30°=∠C.
∴CD=AD=4 cm.
∴BC=BD+CD=8+4=12(cm).
19. 【答案】
解:(1)证明:∵OB=OC,
∴∠OBC=∠OCB.
∵锐角三角形ABC的两条高BD,CE相交于点O,
∴∠BEC=∠CDB=90°.
∵∠BEC+∠BCE+∠ABC=∠CDB+∠DBC+∠ACB=180°,
∴180°-∠BEC-∠BCE=180°-∠CDB-∠DBC,
∴∠ABC=∠ACB,
∴AB=AC,∴△ABC是等腰三角形.
(2)点O在∠BAC的平分线上.
理由:连接AO并延长交BC于点F.
在△AOB和△AOC中,
∴△AOB≌△AOC(SSS),∴∠BAF=∠CAF,
∴点O在∠BAC的平分线上.
20. 【答案】
解:设∠B=x°.
∵DE是AB的垂直平分线,
∴AE=BE,∴∠EAB=∠B=x°.
∵∠CAE∶∠EAB=4∶1,
∴∠CAE=4∠EAB=(4x)°,
∴∠CAB=∠CAE+∠EAB=(5x)°.
∵∠ACB=90°,∴∠CAB+∠B=90°,
即(5x)°+x°=90°,解得x=15,∴∠B=15°.
21. 【答案】
【问题解决】在CD上截取CH=CE,易证△CEH是等边三角形,得出EH=EC=CH,证明△DEH≌△FEC(SAS),得出DH=CF,即可得出结论;
【类比探究】过D作DG∥AB,交AC的延长线于点G,由平行线的性质易证∠GDC=∠DGC=60°,得出△GCD为等边三角形,则DG=CD=CG,证明△EGD≌△FCD(SAS),得出EG=FC,即可得出FC=CD+CE.
【问题解决】证明:在CD上截取CH=CE,如图1所示:
∵△ABC是等边三角形,
∴∠ECH=60°,
∴△CEH是等边三角形,
∴EH=EC=CH,∠CEH=60°,
∵△DEF是等边三角形,
∴DE=FE,∠DEF=60°,
∴∠DEH+∠HEF=∠FEC+∠HEF=60°,
∴∠DEH=∠FEC,
在△DEH和△FEC中,
,
∴△DEH≌△FEC(SAS),
∴DH=CF,
∴CD=CH+DH=CE+CF,
∴CE+CF=CD;
【类比探究】解:线段CE,CF与CD之间的等量关系是FC=CD+CE;理由如下:
∵△ABC是等边三角形,
∴∠A=∠B=60°,
过D作DG∥AB,交AC的延长线于点G,如图2所示:
∵GD∥AB,
∴∠GDC=∠B=60°,∠DGC=∠A=60°,
∴∠GDC=∠DGC=60°,
∴△GCD为等边三角形,
∴DG=CD=CG,∠GDC=60°,
∵△EDF为等边三角形,
∴ED=DF,∠EDF=∠GDC=60°,
∴∠EDG=∠FDC,
在△EGD和△FCD中,
,
∴△EGD≌△FCD(SAS),
∴EG=FC,
∴FC=EG=CG+CE=CD+CE.
A
B
C
D
E
F
一、选择题
1. 如图,在△ABC中,AB=AC,AD,CE分别是△ABC的中线和角平分线.若∠CAD=20°,则∠ACE的度数是( )
A.20° B.35° C.40° D.70°
2. 在△ABC中,与∠A相邻的外角是110°,要使△ABC为等腰三角形,则∠B的度数是( )
A.70° B.55°
C.70°或55° D.70°或55°或40°
3. 如图,以点O为圆心,任意长为半径画弧,与射线OM交于点A,再以点A为圆心,AO长为半径画弧,两弧交于点B,画出射线OB,则∠AOB等于( )
A.30° B.45° C.60° D.90°
4. 如图,下列条件不能推出△ABC是等腰三角形的是( )
A.∠B=∠C B.AD⊥BC,∠BAD=∠CAD
C.AD⊥BC,BD=CD D.AD⊥BC,∠BAD=∠ACD
5. 如图,在△ABC中,∠ABC的平分线交AC于点D,AD=6,过点D作DE∥BC交AB于点E.若△AED的周长为16,则边AB的长为( )
A.6 B.8 C.10 D.12
6. 如图,△ABC是等边三角形,DE∥BC.若AB=10,BD=6,则△ADE的周长为( )
A.4 B.12 C.18 D.30
7. (2020·天门仙桃潜江)如图,已知△ABC和△ADE都是等腰三角形,∠BAC∠DAE90°,BD,CE交于点F,连接AF.下列结论:①BDCE;②BF⊥CF;③AF平分∠CAD;④∠AFE45°.其中正确结论的个数有
A.1 B.2个 C.3个 D.4个
8. (2020·宜宾)如图,△ABC和△ECD都是等边三角形,且点B、C、D在一条直线上,连结BE、AD,点M、N分别是线段BE、AD上的两点,且BM=BE,AN=AD,则△CMN的形状是( )
A.等腰三角形 B.直角三角形 C.等边三角形 D.不等边三角形
二、填空题
9. 如图,∠AOB=30°,点P在OA上,且OP=2,点P关于直线OB的对称点是Q,则PQ=________.
10. (2020·齐齐哈尔)等腰三角形的两条边长分别为3和4,则这个等腰三角形的周长是 .
11. 在△ABC中,若∠A=100°,∠B=40°,AC=5,则AB=________.
12. 如图所示,在△ABC中,DE是AC的垂直平分线,AE=5 cm,△ABD的周长为18 cm,则△ABC的周长为 .
13. 如图,六边形ABCDEF的六个内角都相等.若AB=1,BC=CD=3,DE=2,则这个六边形的周长为________.
14. 如图所示,在△ABC中,∠B=50°,∠C=90°,在射线BA上找一点D,使△ACD为等腰三角形,则∠ADC的度数为________.
15. 如图,在△ABC中,若AB=AC=8,∠A=30°,则S△ABC=________.
16. 规律探究如图,∠BOC=9°,点A在OB上,且OA=1,按下列要求画图:
以A为圆心,1为半径向右画弧交OC于点A1,得第1条线段AA1;
再以A1为圆心,1为半径向右画弧交OB于点A2,得第2条线段A1A2;
再以A2为圆心,1为半径向右画弧交OC于点A3,得第3条线段A2A3……
这样画下去,直到得第n条线段,之后就不能再画出符合要求的线段了,则n=________.
三、解答题
17. 如图,已知△ABC中,D为BC边上一点,且AB=AC=BD,AD=CD,求∠BAC的度数.
18. 如图,在△ABC中,AB=AC,∠C=30°,AD⊥AB交BC于点D,AD=4 cm,求BC的长.
19. 已知:如图所示,锐角三角形ABC的两条高BD,CE相交于点O,且OB=OC.
(1)求证:△ABC是等腰三角形;
(2)判断点O是否在∠BAC的平分线上,并说明理由.
20. 如图所示,在△ABC中,∠ACB=90°,DE是AB的垂直平分线,∠CAE∶∠EAB=4∶1. 求∠B的度数.
21. (12分)如图,在等边三角形ABC中,点E是边AC上一定点,点D是直线BC上一动点,以DE为一边作等边三角形DEF,连接CF.
【问题解决】
如图1,若点D在边BC上,求证:CE+CF=CD;
【类比探究】
如图2,若点D在边BC的延长线上,请探究线段CE,CF与CD之间存在怎样的数量关系?并说明理由.
人教版数学 八年级上册 13.3 等腰三角形 创新训练-答案
一、选择题
1. 【答案】B
2. 【答案】D [解析] 由题意得,∠A=70°,当∠B=∠A=70°时,△ABC为等腰三角形;
当∠B=55°时,可得∠C=55°,∠B=∠C,△ABC为等腰三角形;
当∠B=40°时,可得∠C=70°=∠A,△ABC为等腰三角形.
3. 【答案】C [解析] 连接AB.根据题意得 OB=OA=AB,∴△AOB是等边三角形.∴∠AOB=60°.
4. 【答案】D [解析] 选项A由等角对等边可得△ABC是等腰三角形;选项B由所给条件可得△ADB≌△ADC,由全等三角形的性质可得AB=AC;选项C由垂直平分线的性质可得AB=AC;选项D不可以得到AB=AC.
5. 【答案】C [解析] ∵BD平分∠ABC,
∴∠EBD=∠CBD.
∵DE∥BC,∴∠EDB=∠CBD.
∴∠EBD=∠EDB.∴BE=DE.
∵△AED的周长为16,
∴AE+DE+AD=AE+BE+AD=AB+AD=16.
∵AD=6,∴AB=10.
6. 【答案】B [解析] ∵△ABC为等边三角形,∴∠A=∠B=∠C=60°.∵DE∥BC,∴∠ADE=∠B=60°,∠AED=∠C=60°.∴△ADE为等边三角形.∵AB=10,BD=6,∴AD=AB-BD=10-6=4.∴△ADE的周长为4×3=12.
7. 【答案】C
【解析】∵△ABC和△ADE都是等腰直角三角形,
∴AB=AC,AD=AE,
∵∠BAD=90°+∠CAD,
∠CAE=90°+∠CAD,
∴∠BAD=∠CAE,
在△AEC与△ADB中,
,
∴△AEC≌△ADB(SAS),
∴BD=CE,故①正确;
∴∠ADB=∠AEC,
∵∠DEF+∠AEC+∠EDA=90°,
∴∠DEF+∠ADB+∠EDA=90°
∴∠DEF+∠EDF=90 ,
∴BD⊥CE,故②正确;
∵作AN⊥CE,AM⊥BD
∵△AEC≌△ADB(SAS),
∴AM=AN,
∵AF是∠BFE的角平分线,
∠BFE=90°,
∴∠AFE=45°,故④正确
,故③正确;
因为QF≠PF,故③错误。
正确的有3个,
故选:C.
8. 【答案】 C
【解析】 由△ABC和△ECD都是等边三角形,可得△BCE≌△ACD(SAS),∴∠MBC=∠NAC,BE=AD,∵BM=BE,AN=AD,∴BM=AN,∴△MBC≌△NAC(SAS),∴MC=NC,∠BCM=∠ACN,∵∠BCM+∠MCA=60°,∴∠NCA+∠MCA=60°,∴∠MCN=60°,∴△MCN是等边三角形.
二、填空题
9. 【答案】2 [解析] 如图,连接OQ.
∵点P关于直线OB的对称点是Q,
∴OB垂直平分PQ.
∴∠POB=∠QOB=30°,OP=OQ.∴∠POQ=60°.
∴△POQ为等边三角形.∴PQ=OP=2.
10. 【答案】10或11.
【解析】分3是腰长与底边长两种情况讨论求解即可.①3是腰长时,三角形的三边分别为3、3、4,
∵此时能组成三角形,∴周长=3+3+4=10;
②3是底边长时,三角形的三边分别为3、4、4,此时能组成三角形,所以周长=3+4+4=11.
综上所述,这个等腰三角形的周长是10或11.
故答案为:10或11.
11. 【答案】5
12. 【答案】 28 cm
13. 【答案】15 [解析] 由多边形的内角和定理可知,这个六边形的每个内角都是120°,因此直线AB,CD,EF围成一个等边三角形,且这个等边三角形的边长为7.因此AF=4,EF=2.所以这个六边形的周长=1+3+3+2+2+4=15.
14. 【答案】20°或70°或100° [解析] 如图,有三种情形:
①当AC=AD时,∠ADC=70°;
②当CD′=AD′时,∠AD′C=100°;
③当AC=AD″时,∠AD″C=20°.
15. 【答案】16 [解析] 如图,过点C作CD⊥AB,垂足为D,
则△ADC是含30°角的直角三角形,那么DC=AC=4,∴S△ABC=AB·DC=×8×4=16.
16. 【答案】9
三、解答题
17. 【答案】
解:∵AD=CD,∴设∠DAC=∠C=x°.
∵AB=AC=BD,
∴∠BAD=∠BDA=∠DAC+∠C=2x°,
∠B=∠C=x°.∴∠BAC=3x°.
∵∠B+∠BAC+∠C=180°,∴5x=180,
解得x=36.
∴∠BAC=3x°=108°.
18. 【答案】
解:∵AB=AC,∠C=30°,∴∠B=30°.
∵AB⊥AD,AD=4 cm,∴BD=8 cm.
∵∠ADB=90°-∠B=60°,∠C=30°,
∴∠DAC=30°=∠C.
∴CD=AD=4 cm.
∴BC=BD+CD=8+4=12(cm).
19. 【答案】
解:(1)证明:∵OB=OC,
∴∠OBC=∠OCB.
∵锐角三角形ABC的两条高BD,CE相交于点O,
∴∠BEC=∠CDB=90°.
∵∠BEC+∠BCE+∠ABC=∠CDB+∠DBC+∠ACB=180°,
∴180°-∠BEC-∠BCE=180°-∠CDB-∠DBC,
∴∠ABC=∠ACB,
∴AB=AC,∴△ABC是等腰三角形.
(2)点O在∠BAC的平分线上.
理由:连接AO并延长交BC于点F.
在△AOB和△AOC中,
∴△AOB≌△AOC(SSS),∴∠BAF=∠CAF,
∴点O在∠BAC的平分线上.
20. 【答案】
解:设∠B=x°.
∵DE是AB的垂直平分线,
∴AE=BE,∴∠EAB=∠B=x°.
∵∠CAE∶∠EAB=4∶1,
∴∠CAE=4∠EAB=(4x)°,
∴∠CAB=∠CAE+∠EAB=(5x)°.
∵∠ACB=90°,∴∠CAB+∠B=90°,
即(5x)°+x°=90°,解得x=15,∴∠B=15°.
21. 【答案】
【问题解决】在CD上截取CH=CE,易证△CEH是等边三角形,得出EH=EC=CH,证明△DEH≌△FEC(SAS),得出DH=CF,即可得出结论;
【类比探究】过D作DG∥AB,交AC的延长线于点G,由平行线的性质易证∠GDC=∠DGC=60°,得出△GCD为等边三角形,则DG=CD=CG,证明△EGD≌△FCD(SAS),得出EG=FC,即可得出FC=CD+CE.
【问题解决】证明:在CD上截取CH=CE,如图1所示:
∵△ABC是等边三角形,
∴∠ECH=60°,
∴△CEH是等边三角形,
∴EH=EC=CH,∠CEH=60°,
∵△DEF是等边三角形,
∴DE=FE,∠DEF=60°,
∴∠DEH+∠HEF=∠FEC+∠HEF=60°,
∴∠DEH=∠FEC,
在△DEH和△FEC中,
,
∴△DEH≌△FEC(SAS),
∴DH=CF,
∴CD=CH+DH=CE+CF,
∴CE+CF=CD;
【类比探究】解:线段CE,CF与CD之间的等量关系是FC=CD+CE;理由如下:
∵△ABC是等边三角形,
∴∠A=∠B=60°,
过D作DG∥AB,交AC的延长线于点G,如图2所示:
∵GD∥AB,
∴∠GDC=∠B=60°,∠DGC=∠A=60°,
∴∠GDC=∠DGC=60°,
∴△GCD为等边三角形,
∴DG=CD=CG,∠GDC=60°,
∵△EDF为等边三角形,
∴ED=DF,∠EDF=∠GDC=60°,
∴∠EDG=∠FDC,
在△EGD和△FCD中,
,
∴△EGD≌△FCD(SAS),
∴EG=FC,
∴FC=EG=CG+CE=CD+CE.
A
B
C
D
E
F
