浙江省某重点中学2013届高三10月月考 数学理试题
文档属性
| 名称 | 浙江省某重点中学2013届高三10月月考 数学理试题 |
|
|
| 格式 | zip | ||
| 文件大小 | 201.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-02 00:00:00 | ||
图片预览




文档简介
高三年级第一次月考试卷
数学(理科)
一、选择题:本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项符合题目要求。
1.已知集合,则 ( )
(A)0或 (B)0或3 (C)1或 (D)1或3
2.设f(x)=,则f[f()]= ( )
(A) (B) (C)- (D)
3.若函数,则下列结论正确的是( )
A.,是偶函数 B.,是奇函数
C.,在(0,+∞)上是增函数 D.,在(0,+∞)上是减函数
4.已知在上有两个零点,则的取值范围为( )
A.(1,2) B.[1,2] C.(1,2] D.[1,2)
5.设为的外心,且 ,则的内角的值为
A. B. C. D. 21世纪教育网
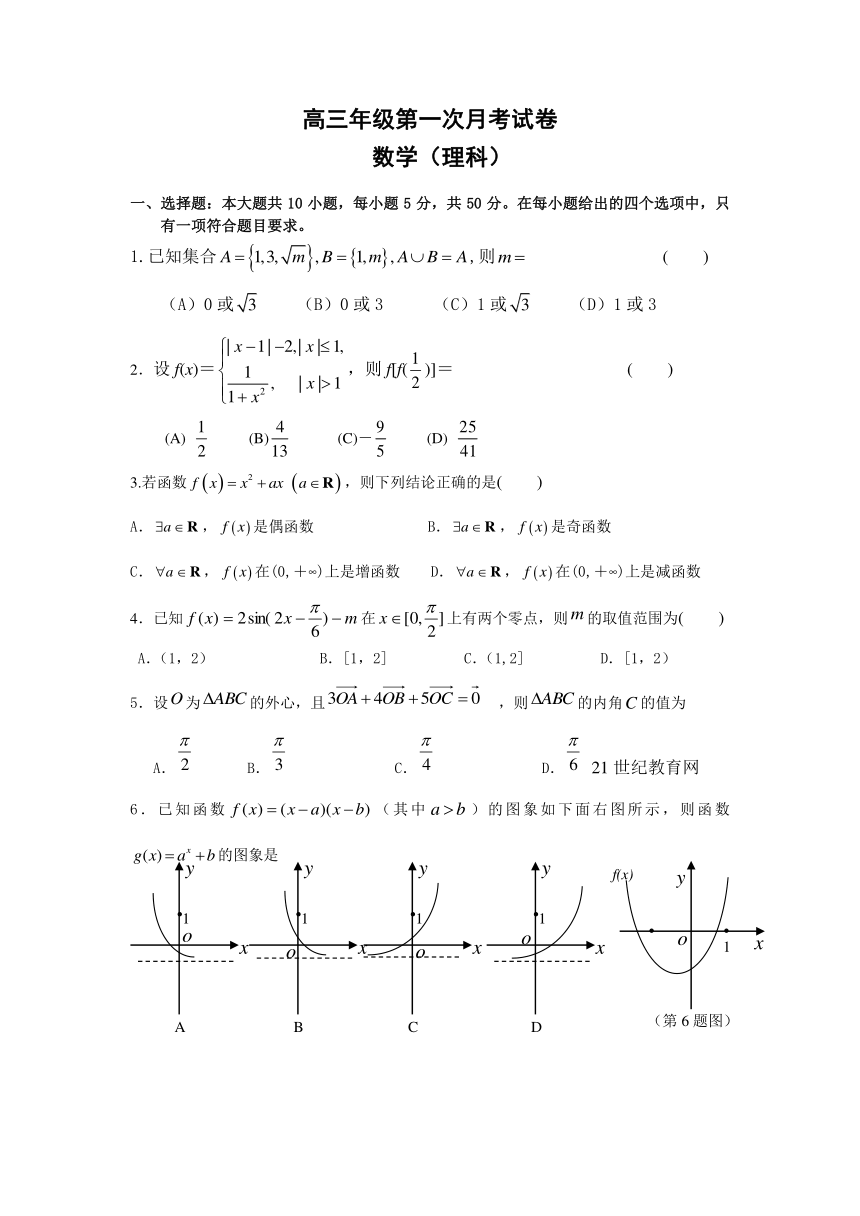
6.已知函数(其中)的图象如下面右图所示,则函数的图象是
7.不等式对任意实数恒成立,则实数的取值范围为
A. B. C. D.
8.设函数的图像关于直线对称,且它的最小正周期为,则
A.的图像经过点 B.在区间上是减函数
C.的最大值为A D.的图像的一个对称中心是
9.若函数f(x)=(a>0且a≠1)在上既是奇函数又是增函数,则
g(x)=的图象是 21世纪教育网
10.10.对实数和,定义运算“”:,设函数,,若函数的图象与轴恰有两个公共点,则实数的取值范围是( )
A. B.
C. D.
二.填空题:本大题共7小题,每小题4分,共28分。
11. 向量的夹角为120°,= .
12. 14. 已知为奇函数,
13.在中,、、所对的边分别为、、,若,、分别
是方程的两个根,则等于______.
14. 已知命题:
1.函数在上是减函数;
2.函数的定义域为R,是为极值点的既不充分也不必要条件;
3.函数的最小正周期为;
4.已知则在方向上的投影为.
其中,正确命题的序号是 .(把你认为正确命题的序号都填上)
15. 若函数,(且)的值域为R,则实数的取值范围是 ______________ ___
16. 定义符号函数 ,则不等式:的解集是__________.21世纪教育网
17.设是定义在上的偶函数,对任意的,都有,且当时,,若关于的方程
在区间内恰有三个不同实根,则实数的取值范围是 .
三.解答题:本大题共5小题,共72分。解答应写出文字说明、证明过程或演算步骤。
18. (本题14分)A、B是直线图像的两个相邻交点,且 21世纪教育网
(1)求的值;
(2)在锐角中,a,b,c分别是角A,B,C的对边,若 的面积为,求a的值.
19.(本题14分)
定义在非零实数集上的函数满足且是区间上的增函数
求的值;
求证:;
解不等式.
20.(本小题满分14分)
(本小题满分14分)已知为函数的一个极值点.
(1)求及函数的单调区间;
(2)若对于任意恒成立,求取值范围.
21.(本小题满分15分)
如图,在平面直角坐标系中,锐角和钝角的终边分别与单位圆交于,两点.
(1)如果,两点的纵坐标分别为,,求和
(2)在(1)的条件下,求的值;
(3)已知点,求函数的值域.
22.(本小题满分15分)
已知函数,, 。
(1)设函数,讨论的极值点的个数;
(2)若,求证:对任意的,且时,都有。
高三第一次月考
数学(理科)答案
1-5 BBADC 6-10 ABDCD11.7 12.6 13.4 14.2,3 15.
16. 17..
19.定义在非零实数集上的函数满足且是区间上的增函数
求的值;
F(1)=0 F(-1)=0 —————————————— 4分
求证:
令y=-1 则 f(-x)=f(x) —————————— 4分
解不等式.
[0,1/2)或(1/2,1] ———————————————— 6分
20.(本小题满分14分)已知为函数的一个极值点.
(1)求及函数的单调区间;
(2)若对于任意恒成立,求取值范围.
解:(1) ……………3分
由得: …………………… …………5分
上单调递增,在(-1,1)上单调递减…21世纪教育网………7分
(2)时,最小值为0
对恒成立,…………10分
分离参数得:,
易知:时…………13分
…………14分
21.解:(Ⅰ)根据三角函数的定义,得,.
又是锐角,所以,.……………………………4分
(Ⅱ)由(Ⅰ)知,,.
又是锐角,是钝角,
所以 ,.
所以 .……9分
(Ⅲ)由题意可知,,.
所以 ,
因为 ,所以,
所以函数的值域为.……………………………14分
22.(本小题满分15分)
解:解:(1)
,,,,得
当时,,
从而在上单调递减,
当时,,
从而在上单调递增,
所以,
当,即时,恒成立,的极值点个数为;
当,即时,(又
)
的极值点个数为个]
(注:用 与的图像讨论也可)
(2)证明:
21世纪教育网
在上单调递增
在上恒成立21世纪教育网
令,关于是一次函数。
又,,(由得)
所以在上恒成立,所以,原命题成立。
(注:转化为恒成立,分三种情况讨论的最大值)21世纪教育网
数学(理科)
一、选择题:本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项符合题目要求。
1.已知集合,则 ( )
(A)0或 (B)0或3 (C)1或 (D)1或3
2.设f(x)=,则f[f()]= ( )
(A) (B) (C)- (D)
3.若函数,则下列结论正确的是( )
A.,是偶函数 B.,是奇函数
C.,在(0,+∞)上是增函数 D.,在(0,+∞)上是减函数
4.已知在上有两个零点,则的取值范围为( )
A.(1,2) B.[1,2] C.(1,2] D.[1,2)
5.设为的外心,且 ,则的内角的值为
A. B. C. D. 21世纪教育网
6.已知函数(其中)的图象如下面右图所示,则函数的图象是
7.不等式对任意实数恒成立,则实数的取值范围为
A. B. C. D.
8.设函数的图像关于直线对称,且它的最小正周期为,则
A.的图像经过点 B.在区间上是减函数
C.的最大值为A D.的图像的一个对称中心是
9.若函数f(x)=(a>0且a≠1)在上既是奇函数又是增函数,则
g(x)=的图象是 21世纪教育网
10.10.对实数和,定义运算“”:,设函数,,若函数的图象与轴恰有两个公共点,则实数的取值范围是( )
A. B.
C. D.
二.填空题:本大题共7小题,每小题4分,共28分。
11. 向量的夹角为120°,= .
12. 14. 已知为奇函数,
13.在中,、、所对的边分别为、、,若,、分别
是方程的两个根,则等于______.
14. 已知命题:
1.函数在上是减函数;
2.函数的定义域为R,是为极值点的既不充分也不必要条件;
3.函数的最小正周期为;
4.已知则在方向上的投影为.
其中,正确命题的序号是 .(把你认为正确命题的序号都填上)
15. 若函数,(且)的值域为R,则实数的取值范围是 ______________ ___
16. 定义符号函数 ,则不等式:的解集是__________.21世纪教育网
17.设是定义在上的偶函数,对任意的,都有,且当时,,若关于的方程
在区间内恰有三个不同实根,则实数的取值范围是 .
三.解答题:本大题共5小题,共72分。解答应写出文字说明、证明过程或演算步骤。
18. (本题14分)A、B是直线图像的两个相邻交点,且 21世纪教育网
(1)求的值;
(2)在锐角中,a,b,c分别是角A,B,C的对边,若 的面积为,求a的值.
19.(本题14分)
定义在非零实数集上的函数满足且是区间上的增函数
求的值;
求证:;
解不等式.
20.(本小题满分14分)
(本小题满分14分)已知为函数的一个极值点.
(1)求及函数的单调区间;
(2)若对于任意恒成立,求取值范围.
21.(本小题满分15分)
如图,在平面直角坐标系中,锐角和钝角的终边分别与单位圆交于,两点.
(1)如果,两点的纵坐标分别为,,求和
(2)在(1)的条件下,求的值;
(3)已知点,求函数的值域.
22.(本小题满分15分)
已知函数,, 。
(1)设函数,讨论的极值点的个数;
(2)若,求证:对任意的,且时,都有。
高三第一次月考
数学(理科)答案
1-5 BBADC 6-10 ABDCD11.7 12.6 13.4 14.2,3 15.
16. 17..
19.定义在非零实数集上的函数满足且是区间上的增函数
求的值;
F(1)=0 F(-1)=0 —————————————— 4分
求证:
令y=-1 则 f(-x)=f(x) —————————— 4分
解不等式.
[0,1/2)或(1/2,1] ———————————————— 6分
20.(本小题满分14分)已知为函数的一个极值点.
(1)求及函数的单调区间;
(2)若对于任意恒成立,求取值范围.
解:(1) ……………3分
由得: …………………… …………5分
上单调递增,在(-1,1)上单调递减…21世纪教育网………7分
(2)时,最小值为0
对恒成立,…………10分
分离参数得:,
易知:时…………13分
…………14分
21.解:(Ⅰ)根据三角函数的定义,得,.
又是锐角,所以,.……………………………4分
(Ⅱ)由(Ⅰ)知,,.
又是锐角,是钝角,
所以 ,.
所以 .……9分
(Ⅲ)由题意可知,,.
所以 ,
因为 ,所以,
所以函数的值域为.……………………………14分
22.(本小题满分15分)
解:解:(1)
,,,,得
当时,,
从而在上单调递减,
当时,,
从而在上单调递增,
所以,
当,即时,恒成立,的极值点个数为;
当,即时,(又
)
的极值点个数为个]
(注:用 与的图像讨论也可)
(2)证明:
21世纪教育网
在上单调递增
在上恒成立21世纪教育网
令,关于是一次函数。
又,,(由得)
所以在上恒成立,所以,原命题成立。
(注:转化为恒成立,分三种情况讨论的最大值)21世纪教育网
同课章节目录
