沪科版数学八年级上册 13.2 命题的证明课件(共18张PPT)
文档属性
| 名称 | 沪科版数学八年级上册 13.2 命题的证明课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-01 11:14:09 | ||
图片预览




文档简介
(共18张PPT)
命题的证明
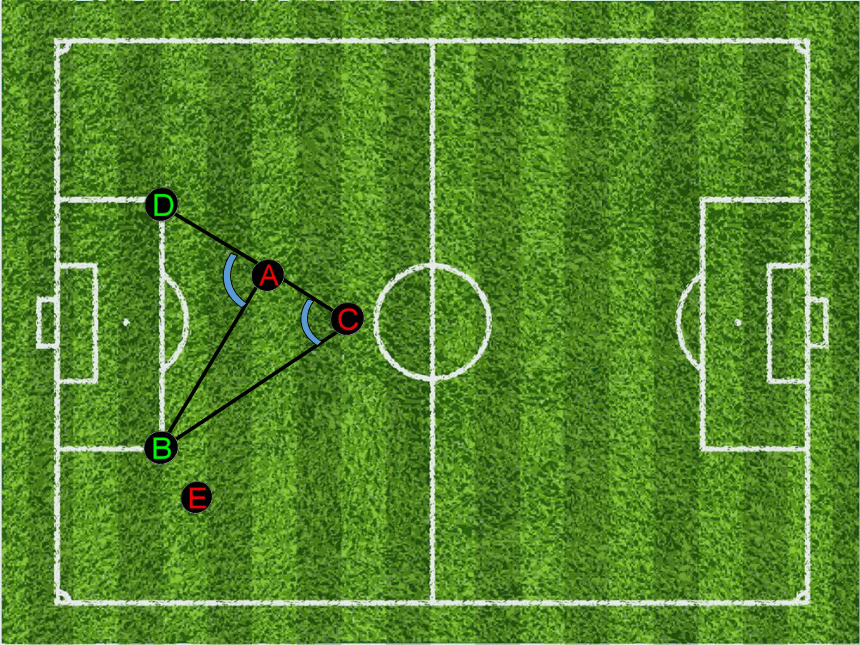
三角形外角及其性质
一、复习回顾
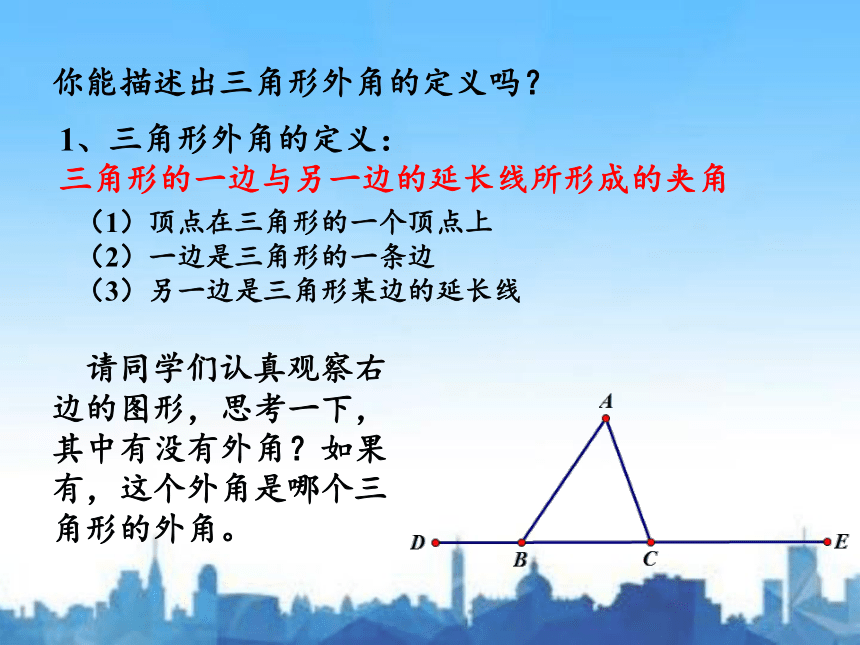
你能描述出三角形外角的定义吗?
1、三角形外角的定义:
三角形的一边与另一边的延长线所形成的夹角
请同学们认真观察右边的图形,思考一下,其中有没有外角?如果有,这个外角是哪个三角形的外角。
(1)顶点在三角形的一个顶点上
(2)一边是三角形的一条边
(3)另一边是三角形某边的延长线
一个三角形到底有几个外角?
外角与内角
在位置上有
什么关系?
外角与内角
在数量上有
什么关系?
三角形外角
相互之间有
什么关系?
二、学习目标
1、了解三角形外角的概念
2、掌握三角形的外角的两个性质
3、能利用三角形的外角性质解决简单的实际问题
三、思考探究
B
C
A
1
D
2
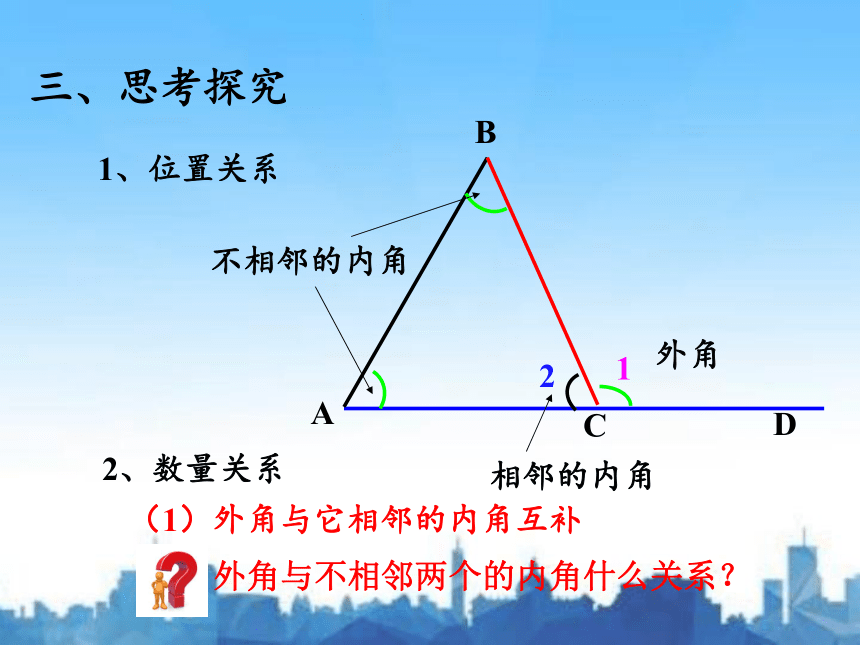
相邻的内角
不相邻的内角
外角
1、位置关系
2、数量关系
(1)外角与它相邻的内角互补
外角与不相邻两个的内角什么关系?
(1)动手拼一拼
C
B
A
D
在一张白纸上任意画一个三角形ABC,延长BA到点D把∠B、∠C剪下拼在一起,放到∠CAD上,看看会出现什么结果?
(2)拿尺量一量
用量角器把刚才剪下来的角
量一量,然后看看这些角度之
间有什么关系?
∠CAD= ∠B+ ∠C
3、推理证一证:
如右图所示,CD是BC边的延长线
求证: ∠ACD= ∠A+ ∠B
方法一、
证明:如图所示
∵ ∠A、∠B、 ∠ ACB是△ ABC的内角
∴ ∠A+∠B+∠ ACB =1800
又∵ ∠ACD+∠ ACB =1800
∴∠ACD =∠ A+∠B
1
2
方法二、
证明:如图,过C点CE//AB
∴ ∠A=∠2、∠ B = ∠ 1
∴ ∠ACD =∠ 1+ ∠2=∠ A+∠B
E
三角形外角性质1
三角形的一个外角等于和它不相邻的两个内角之和
∠ACD= ∠A+ ∠B
三角形外角性质2
三角形的一个外角大于任何一个与它不相邻的内角
∠ACD > ∠A ∠ACD > ∠B
α
120
35
∠α=( )
四、应用新知
(1)求下列各图中∠α的度数
α
45
95
∠α=( )
α
25
∠α=( )
(2)判断题
1、三角形的外角等于任意两个内角的和。( )
2、三角形的一个外角大于任何一个内角。( )
(3)判断∠1与∠3的大小,并说明理由。
∠3 >∠1 理由如下:
如图所示∵ ∠3是△ ADE的一个外角
∴ ∠3 > ∠2
∵ ∠2是△ ABC的一个外角
∴ ∠2 > ∠1
∴∠3 >∠1
解:
(4)如图,计算∠BOC的度数
450
250
300
解:如图,延长BO交AC于点D
∵ ∠1是△ABD的一个外角
∴ ∠1=∠ B +∠A
∵ ∠BOC是△ODC的一个外角
∴ ∠BOC = ∠1+∠C
∴∠BOC= ∠B+∠A+∠C=250+450+300 =1000
D
1
(5)在△ ABC中,AD、BE、CF分别为
三角形三边的延长线。
求∠1+ ∠2+ ∠3
A
B
C
D
E
F
1
2
3
五、课堂小结
1、三角形外角的定义
三角形一边与另一边的延长线所形成的夹角
2、三角形外角的性质
(1):三角形的外角等于和它不相邻的两个内角之和
(2):三角形的外角大于与它不相邻的任何一个内角
3、两个模型:小旗模型和飞镖模型
作业:课本83页练习题第1、2题
课本85页习题13.2第9题
谢 谢
命题的证明
三角形外角及其性质
一、复习回顾
你能描述出三角形外角的定义吗?
1、三角形外角的定义:
三角形的一边与另一边的延长线所形成的夹角
请同学们认真观察右边的图形,思考一下,其中有没有外角?如果有,这个外角是哪个三角形的外角。
(1)顶点在三角形的一个顶点上
(2)一边是三角形的一条边
(3)另一边是三角形某边的延长线
一个三角形到底有几个外角?
外角与内角
在位置上有
什么关系?
外角与内角
在数量上有
什么关系?
三角形外角
相互之间有
什么关系?
二、学习目标
1、了解三角形外角的概念
2、掌握三角形的外角的两个性质
3、能利用三角形的外角性质解决简单的实际问题
三、思考探究
B
C
A
1
D
2
相邻的内角
不相邻的内角
外角
1、位置关系
2、数量关系
(1)外角与它相邻的内角互补
外角与不相邻两个的内角什么关系?
(1)动手拼一拼
C
B
A
D
在一张白纸上任意画一个三角形ABC,延长BA到点D把∠B、∠C剪下拼在一起,放到∠CAD上,看看会出现什么结果?
(2)拿尺量一量
用量角器把刚才剪下来的角
量一量,然后看看这些角度之
间有什么关系?
∠CAD= ∠B+ ∠C
3、推理证一证:
如右图所示,CD是BC边的延长线
求证: ∠ACD= ∠A+ ∠B
方法一、
证明:如图所示
∵ ∠A、∠B、 ∠ ACB是△ ABC的内角
∴ ∠A+∠B+∠ ACB =1800
又∵ ∠ACD+∠ ACB =1800
∴∠ACD =∠ A+∠B
1
2
方法二、
证明:如图,过C点CE//AB
∴ ∠A=∠2、∠ B = ∠ 1
∴ ∠ACD =∠ 1+ ∠2=∠ A+∠B
E
三角形外角性质1
三角形的一个外角等于和它不相邻的两个内角之和
∠ACD= ∠A+ ∠B
三角形外角性质2
三角形的一个外角大于任何一个与它不相邻的内角
∠ACD > ∠A ∠ACD > ∠B
α
120
35
∠α=( )
四、应用新知
(1)求下列各图中∠α的度数
α
45
95
∠α=( )
α
25
∠α=( )
(2)判断题
1、三角形的外角等于任意两个内角的和。( )
2、三角形的一个外角大于任何一个内角。( )
(3)判断∠1与∠3的大小,并说明理由。
∠3 >∠1 理由如下:
如图所示∵ ∠3是△ ADE的一个外角
∴ ∠3 > ∠2
∵ ∠2是△ ABC的一个外角
∴ ∠2 > ∠1
∴∠3 >∠1
解:
(4)如图,计算∠BOC的度数
450
250
300
解:如图,延长BO交AC于点D
∵ ∠1是△ABD的一个外角
∴ ∠1=∠ B +∠A
∵ ∠BOC是△ODC的一个外角
∴ ∠BOC = ∠1+∠C
∴∠BOC= ∠B+∠A+∠C=250+450+300 =1000
D
1
(5)在△ ABC中,AD、BE、CF分别为
三角形三边的延长线。
求∠1+ ∠2+ ∠3
A
B
C
D
E
F
1
2
3
五、课堂小结
1、三角形外角的定义
三角形一边与另一边的延长线所形成的夹角
2、三角形外角的性质
(1):三角形的外角等于和它不相邻的两个内角之和
(2):三角形的外角大于与它不相邻的任何一个内角
3、两个模型:小旗模型和飞镖模型
作业:课本83页练习题第1、2题
课本85页习题13.2第9题
谢 谢
