沪科版数学九年级上册 23.2 解直角三角形及其应用 课件(共25张PPT)
文档属性
| 名称 | 沪科版数学九年级上册 23.2 解直角三角形及其应用 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-01 00:00:00 | ||
图片预览




文档简介
(共25张PPT)
23.2 解直角三角形及其应用
知识要点梳理
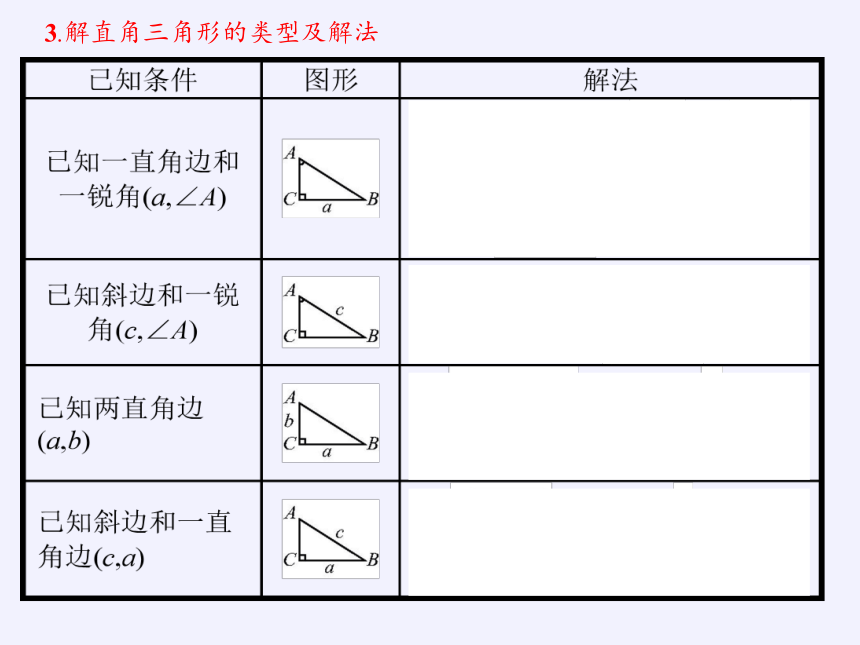
3.解直角三角形的类型及解法
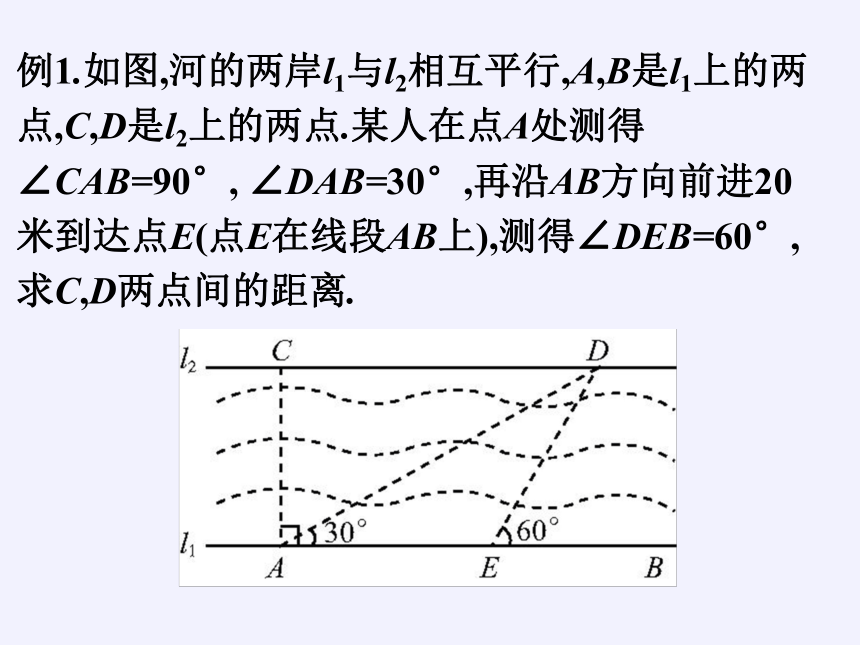
例1.如图,河的两岸l1与l2相互平行,A,B是l1上的两点,C,D是l2上的两点.某人在点A处测得∠CAB=90°, ∠DAB=30°,再沿AB方向前进20米到达点E(点E在线段AB上),测得∠DEB=60°,求C,D两点间的距离.
解:过点D作l1的垂线,垂足为点F,
∵∠DEB=60°,∠DAB=30°,
∴∠ADE=∠DEB-∠DAB=30°,
∴△ADE为等腰三角形,
∴DE=AE=20(米),
在Rt△DEF中,EF=DE·cos 60°=20× =10(米).
∵DF⊥AF,∴∠DFB=90°,∴AC∥DF,
由已知l1∥l2,∴CD∥AF,
∴四边形ACDF为矩形,
∴CD=AF=AE+EF=30(米),
答:C,D两点间的距离为30米.
北偏东45°
例2 芜湖长江大桥是中国跨度最大的公路和铁路两用桥梁,大桥采用低塔斜拉桥桥型(如甲图),图乙是从图甲引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索CD与水平桥面的夹角是60°,两拉索顶端的距离BC为2米,两拉索底端距离AD为20米,请求出立柱BH的长.(结果精确到0.1米, ≈1.732)
归纳:
在解双直角三角形组成图形时
(1)若其中一个直角三角形可解,先解这个直角三角形,再利用两个直角三角形的公共特点,解另一个直角三角形(比如例1)
(2)若两个直角三角形都不可解,可利用两个直角三角形的公共部分(公共边或公共角)列方程求解(比如例2)。
例3 在一次课外实践活动中,同学们要测量某公园人工湖两侧A,B两个凉亭之间的距离.如图,现测得∠ABC=30°, ∠BAC=15°,AC=200米,请计算A,B两个凉亭之间的距离.(结果精确到1米,参考数据:
【答案】如图,过点A作AD⊥BC,交BC的延长线于点D,
∵∠B=30°,
∴∠BAD=60°,
又∵∠BAC=15°,
∴∠CAD=45°,
在Rt△ACD中,∵AC=200米,
归纳:在解斜三角形时,需要作垂线构造直角三角形求解,特别是注意利用30度、45度和60度这些特殊角。
巩固练习
备用练习. 在东西方向的海岸线l上有一长为1 km的码头MN(如图),在码头西端M的正西19.5 km处有一观察站A.某时刻测得一艘匀速直线航行的轮船位于A的北偏西30°,且与A相距40 km的B处;经过1小时20分钟,又测得该轮船位于A的北偏东60°,且与A相距8km的C处.
(1)求该轮船航行的速度(保留精确结果).
(2)如果该轮船不改变航向继续航行,那么轮船能否正好行至码头MN靠岸 请说明理由.
∵BR∥CS,∴△STC∽△RTB,
解得ST=8.
∴AT=12+8=20.
又∵AM=19.5,MN长为1,∴AN=20.5,
∵19.5∴轮船能够正好行至码头MN靠岸.
【方法指导】正确理解方向角的概念是解题的关键,同时把所求线段放入到合适的直角三角形中,才能找到解决问题的思路.
谢 谢
23.2 解直角三角形及其应用
知识要点梳理
3.解直角三角形的类型及解法
例1.如图,河的两岸l1与l2相互平行,A,B是l1上的两点,C,D是l2上的两点.某人在点A处测得∠CAB=90°, ∠DAB=30°,再沿AB方向前进20米到达点E(点E在线段AB上),测得∠DEB=60°,求C,D两点间的距离.
解:过点D作l1的垂线,垂足为点F,
∵∠DEB=60°,∠DAB=30°,
∴∠ADE=∠DEB-∠DAB=30°,
∴△ADE为等腰三角形,
∴DE=AE=20(米),
在Rt△DEF中,EF=DE·cos 60°=20× =10(米).
∵DF⊥AF,∴∠DFB=90°,∴AC∥DF,
由已知l1∥l2,∴CD∥AF,
∴四边形ACDF为矩形,
∴CD=AF=AE+EF=30(米),
答:C,D两点间的距离为30米.
北偏东45°
例2 芜湖长江大桥是中国跨度最大的公路和铁路两用桥梁,大桥采用低塔斜拉桥桥型(如甲图),图乙是从图甲引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索CD与水平桥面的夹角是60°,两拉索顶端的距离BC为2米,两拉索底端距离AD为20米,请求出立柱BH的长.(结果精确到0.1米, ≈1.732)
归纳:
在解双直角三角形组成图形时
(1)若其中一个直角三角形可解,先解这个直角三角形,再利用两个直角三角形的公共特点,解另一个直角三角形(比如例1)
(2)若两个直角三角形都不可解,可利用两个直角三角形的公共部分(公共边或公共角)列方程求解(比如例2)。
例3 在一次课外实践活动中,同学们要测量某公园人工湖两侧A,B两个凉亭之间的距离.如图,现测得∠ABC=30°, ∠BAC=15°,AC=200米,请计算A,B两个凉亭之间的距离.(结果精确到1米,参考数据:
【答案】如图,过点A作AD⊥BC,交BC的延长线于点D,
∵∠B=30°,
∴∠BAD=60°,
又∵∠BAC=15°,
∴∠CAD=45°,
在Rt△ACD中,∵AC=200米,
归纳:在解斜三角形时,需要作垂线构造直角三角形求解,特别是注意利用30度、45度和60度这些特殊角。
巩固练习
备用练习. 在东西方向的海岸线l上有一长为1 km的码头MN(如图),在码头西端M的正西19.5 km处有一观察站A.某时刻测得一艘匀速直线航行的轮船位于A的北偏西30°,且与A相距40 km的B处;经过1小时20分钟,又测得该轮船位于A的北偏东60°,且与A相距8km的C处.
(1)求该轮船航行的速度(保留精确结果).
(2)如果该轮船不改变航向继续航行,那么轮船能否正好行至码头MN靠岸 请说明理由.
∵BR∥CS,∴△STC∽△RTB,
解得ST=8.
∴AT=12+8=20.
又∵AM=19.5,MN长为1,∴AN=20.5,
∵19.5
【方法指导】正确理解方向角的概念是解题的关键,同时把所求线段放入到合适的直角三角形中,才能找到解决问题的思路.
谢 谢
