华东师大版数学八年级上册 14.2 勾股定理的应用教案
文档属性
| 名称 | 华东师大版数学八年级上册 14.2 勾股定理的应用教案 |  | |
| 格式 | doc | ||
| 文件大小 | 76.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-01 20:41:45 | ||
图片预览

文档简介
任课教师 年级 初二 科目 数学 授课时间
课 题 利用勾股定理解决折叠问题 课型 习题课 课时 1
教学目标 知识与技能 1、理解折叠问题的实质,掌握解题步骤,明确解决问题的突破口;2、能正确利用勾股定理解决折叠问题,进行直角三角形有关的计算。
过程与方法 经历观察、比较,发现折叠的过程,在讨论类比中探索勾股定理解决折叠问题的方法。
情感态度与价值观 1、在与同学交流讨论中,学会倾听、思考,大胆发表自己的观点,并体验学习的快乐,养成严谨认真的解题习惯;2、通过图形的折叠,渗透全等、对称图形的意识。
教学重点难点 教学重点 1、探究折叠前后图形的变化特点和规律;·2、利用勾股定理解决折叠问题;3、教师怎样引导学生进行对问题的探讨,启发学生归纳、综合应用
教学难点 1、折叠前后元素对应关系2、利用勾股定理解决折叠问题;3、教师怎样引导学生进行对问题的探讨,启发学生归纳、综合应用。
教学方法 启发式、探究式
教学用具 多媒体、纸片、三角尺、笔
教 学 过 程
教 师 活 动、教 学 内 容 学 生 活 动
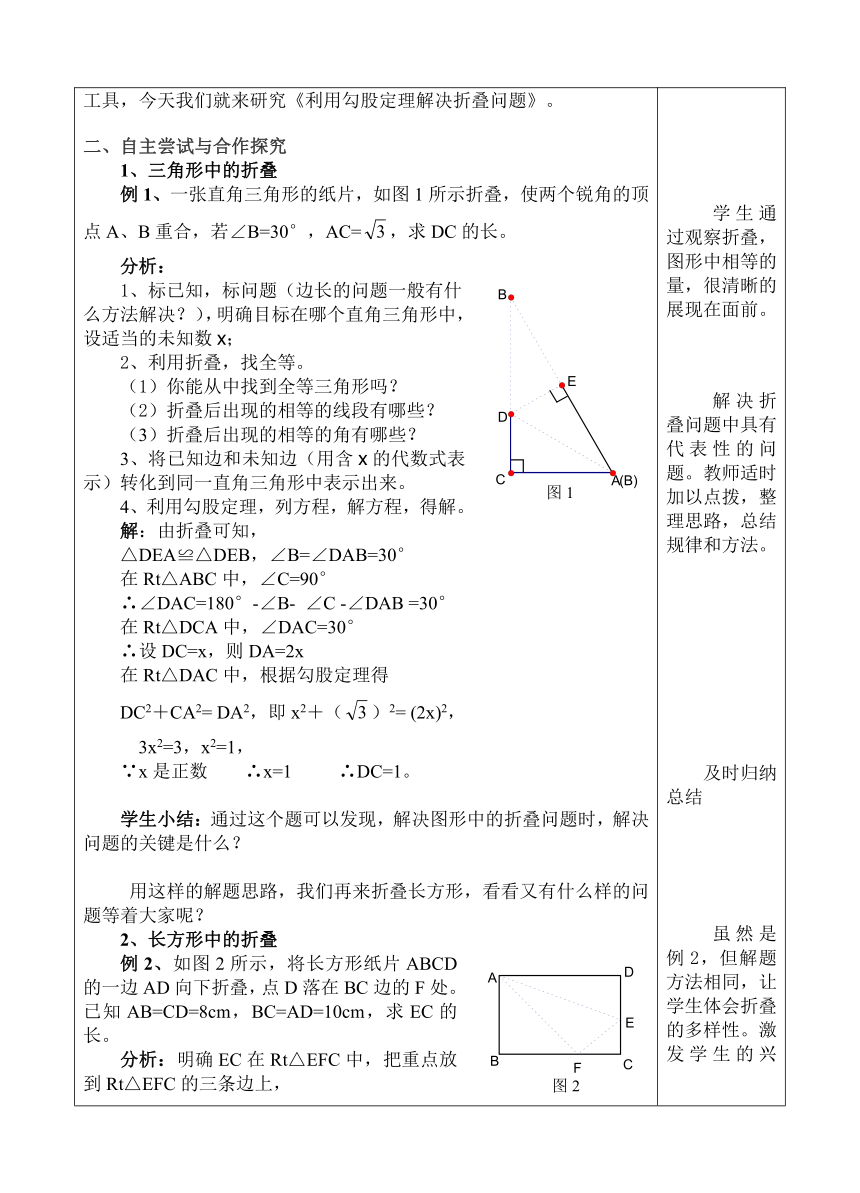
一、引入课题前面我们学习了勾股定理,它是用来求直角三角形中边长的基本工具,今天我们就来研究《利用勾股定理解决折叠问题》。二、自主尝试与合作探究1、三角形中的折叠例1、一张直角三角形的纸片,如图1所示折叠,使两个锐角的顶点A、B重合,若∠B=30°,AC=,求DC的长。分析:1、标已知,标问题(边长的问题一般有什么方法解决?),明确目标在哪个直角三角形中,设适当的未知数x;2、利用折叠,找全等。(1)你能从中找到全等三角形吗?(2)折叠后出现的相等的线段有哪些?(3)折叠后出现的相等的角有哪些?3、将已知边和未知边(用含x的代数式表示)转化到同一直角三角形中表示出来。4、利用勾股定理,列方程,解方程,得解。解:由折叠可知, △DEA≌△DEB,∠B=∠DAB=30°在Rt△ABC中,∠C=90° ∴∠DAC=180°-∠B- ∠C -∠DAB =30°在Rt△DCA中,∠DAC=30°∴设DC=x,则DA=2x在Rt△DAC中,根据勾股定理得DC2+CA2= DA2,即x2+()2= (2x)2,3x2=3,x2=1,∵x是正数 ∴x=1 ∴DC=1。学生小结:通过这个题可以发现,解决图形中的折叠问题时,解决问题的关键是什么?用这样的解题思路,我们再来折叠长方形,看看又有什么样的问题等着大家呢?2、长方形中的折叠例2、如图2所示,将长方形纸片ABCD的一边AD向下折叠,点D落在BC边的F处。已知AB=CD=8cm,BC=AD=10cm,求EC的长。分析:明确EC在Rt△EFC中,把重点放到Rt△EFC的三条边上,根据折叠可以知道△AFE≌△ADE,其中AF=AD=10cm,EF=ED,∠AFE=90°,并且EF+EC=DC=8cm。在Rt△ABF中,根据勾股定理可以得出BF=6,则FC=4,在Rt△FEC中,可以设EC=x,则EF=8-x,根据勾股定理可以得EC2+FC2=EF2,即x2+42=(8-x)2。解:由折叠可得,△AFE≌△ADE,∴AF=AD=10cm,EF=ED,AB=8 cm,EF+EC=DC=8cm,在Rt△ABF中,根据勾股定理得,∴FC=BC-BF=4cm,设EC=xcm,则EF=DC-EC=(8-x)cm,在Rt△EFC中,根据勾股定理得EC2+FC2=EF2,即x2+42=(8-x)2,x=3cm,∴EC的长为3cm。解题步骤归纳:1、标已知,标问题(边长的问题一般有什么方法解决?),明确目标在哪个直角三角形中,设适当的未知数x;2、利用折叠,找全等。3、将已知边和未知边(用含x的代数式表示)转化到同一直角三角形中表示出来。4、利用勾股定理,列出方程,解方程,得解。3、拓展训练长方形还可以怎样折叠,要求折叠一次,给出两个已知条件,提出问题,并解答问题。(提前让学生在课下研究,参考资料,体验折叠的多样性,并灵活运用折叠前后的特点以及勾股定理解决问题)常见折叠方法:让设计成功的学生上台展示他们的成果,并给同学思考时间,在让展示的学生讲解。老师补充。设计意图:举一反三,让学生运用学会的方法和思路来解决问题,形成触类旁通的数学能力。要充分相信学生,多数题目学生可以当“老师”,完全可以讲明白,在不断学习中使数学能力得到提高。三、课堂小结这节课你学到了什么?四、板书设计利用勾股定理解决折叠问题 解题步骤 例1 例21、标、设2、找3、转4、列、解方程,得解.: 五、课后反思 学生通过观察折叠,图形中相等的量,很清晰的展现在面前。解决折叠问题中具有代表性的问题。教师适时加以点拨,整理思路,总结规律和方法。及时归纳总结虽然是例2,但解题方法相同,让学生体会折叠的多样性。激发学生的兴趣。学生上台完成。其余同学,下面完成。并由板书的同学讲解。展示环节是学生展示自我,体验成功的重要手段。师生评价与生生评价相结合。成果展示,提炼方法对学生进行知识、方法、能力梳理,引导学生自己去发现问题,解决问题,从而形成能力。进一步提高学生综合解决数学问题的能力,掌握数学方法和技能。但总体的解题方法不变。
图2
图2
图1
课 题 利用勾股定理解决折叠问题 课型 习题课 课时 1
教学目标 知识与技能 1、理解折叠问题的实质,掌握解题步骤,明确解决问题的突破口;2、能正确利用勾股定理解决折叠问题,进行直角三角形有关的计算。
过程与方法 经历观察、比较,发现折叠的过程,在讨论类比中探索勾股定理解决折叠问题的方法。
情感态度与价值观 1、在与同学交流讨论中,学会倾听、思考,大胆发表自己的观点,并体验学习的快乐,养成严谨认真的解题习惯;2、通过图形的折叠,渗透全等、对称图形的意识。
教学重点难点 教学重点 1、探究折叠前后图形的变化特点和规律;·2、利用勾股定理解决折叠问题;3、教师怎样引导学生进行对问题的探讨,启发学生归纳、综合应用
教学难点 1、折叠前后元素对应关系2、利用勾股定理解决折叠问题;3、教师怎样引导学生进行对问题的探讨,启发学生归纳、综合应用。
教学方法 启发式、探究式
教学用具 多媒体、纸片、三角尺、笔
教 学 过 程
教 师 活 动、教 学 内 容 学 生 活 动
一、引入课题前面我们学习了勾股定理,它是用来求直角三角形中边长的基本工具,今天我们就来研究《利用勾股定理解决折叠问题》。二、自主尝试与合作探究1、三角形中的折叠例1、一张直角三角形的纸片,如图1所示折叠,使两个锐角的顶点A、B重合,若∠B=30°,AC=,求DC的长。分析:1、标已知,标问题(边长的问题一般有什么方法解决?),明确目标在哪个直角三角形中,设适当的未知数x;2、利用折叠,找全等。(1)你能从中找到全等三角形吗?(2)折叠后出现的相等的线段有哪些?(3)折叠后出现的相等的角有哪些?3、将已知边和未知边(用含x的代数式表示)转化到同一直角三角形中表示出来。4、利用勾股定理,列方程,解方程,得解。解:由折叠可知, △DEA≌△DEB,∠B=∠DAB=30°在Rt△ABC中,∠C=90° ∴∠DAC=180°-∠B- ∠C -∠DAB =30°在Rt△DCA中,∠DAC=30°∴设DC=x,则DA=2x在Rt△DAC中,根据勾股定理得DC2+CA2= DA2,即x2+()2= (2x)2,3x2=3,x2=1,∵x是正数 ∴x=1 ∴DC=1。学生小结:通过这个题可以发现,解决图形中的折叠问题时,解决问题的关键是什么?用这样的解题思路,我们再来折叠长方形,看看又有什么样的问题等着大家呢?2、长方形中的折叠例2、如图2所示,将长方形纸片ABCD的一边AD向下折叠,点D落在BC边的F处。已知AB=CD=8cm,BC=AD=10cm,求EC的长。分析:明确EC在Rt△EFC中,把重点放到Rt△EFC的三条边上,根据折叠可以知道△AFE≌△ADE,其中AF=AD=10cm,EF=ED,∠AFE=90°,并且EF+EC=DC=8cm。在Rt△ABF中,根据勾股定理可以得出BF=6,则FC=4,在Rt△FEC中,可以设EC=x,则EF=8-x,根据勾股定理可以得EC2+FC2=EF2,即x2+42=(8-x)2。解:由折叠可得,△AFE≌△ADE,∴AF=AD=10cm,EF=ED,AB=8 cm,EF+EC=DC=8cm,在Rt△ABF中,根据勾股定理得,∴FC=BC-BF=4cm,设EC=xcm,则EF=DC-EC=(8-x)cm,在Rt△EFC中,根据勾股定理得EC2+FC2=EF2,即x2+42=(8-x)2,x=3cm,∴EC的长为3cm。解题步骤归纳:1、标已知,标问题(边长的问题一般有什么方法解决?),明确目标在哪个直角三角形中,设适当的未知数x;2、利用折叠,找全等。3、将已知边和未知边(用含x的代数式表示)转化到同一直角三角形中表示出来。4、利用勾股定理,列出方程,解方程,得解。3、拓展训练长方形还可以怎样折叠,要求折叠一次,给出两个已知条件,提出问题,并解答问题。(提前让学生在课下研究,参考资料,体验折叠的多样性,并灵活运用折叠前后的特点以及勾股定理解决问题)常见折叠方法:让设计成功的学生上台展示他们的成果,并给同学思考时间,在让展示的学生讲解。老师补充。设计意图:举一反三,让学生运用学会的方法和思路来解决问题,形成触类旁通的数学能力。要充分相信学生,多数题目学生可以当“老师”,完全可以讲明白,在不断学习中使数学能力得到提高。三、课堂小结这节课你学到了什么?四、板书设计利用勾股定理解决折叠问题 解题步骤 例1 例21、标、设2、找3、转4、列、解方程,得解.: 五、课后反思 学生通过观察折叠,图形中相等的量,很清晰的展现在面前。解决折叠问题中具有代表性的问题。教师适时加以点拨,整理思路,总结规律和方法。及时归纳总结虽然是例2,但解题方法相同,让学生体会折叠的多样性。激发学生的兴趣。学生上台完成。其余同学,下面完成。并由板书的同学讲解。展示环节是学生展示自我,体验成功的重要手段。师生评价与生生评价相结合。成果展示,提炼方法对学生进行知识、方法、能力梳理,引导学生自己去发现问题,解决问题,从而形成能力。进一步提高学生综合解决数学问题的能力,掌握数学方法和技能。但总体的解题方法不变。
图2
图2
图1
