2022年职高数学吉祥课件 3.1正弦型函数的概念 (共20张PPT)
文档属性
| 名称 | 2022年职高数学吉祥课件 3.1正弦型函数的概念 (共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-31 00:00:00 | ||
图片预览






文档简介
(共20张PPT)
§15 三角函数及其应用
3.1正弦型函数的概念
cos( - )=cos ·cos +sin ·sin
两角和(差)的余弦公式
cos( + )=cos ·cos -sin ·sin
两角差的正弦公式
sin( + )=sin ·cos +cos ·sin
sin( - )=sin ·cos -cos ·sin
公式中的 、 可以是任意角.
两角和(差)的正切公式
公式中的 、 、 + 、 - 都不等于 .
sin2 =2sin ·cos
二倍角的正弦公式
cos2 =cos2 -sin2
或 cos2 =2cos2 -1
或 cos2 =1-2sin2
二倍角的余弦公式
公式中的 可以是任意角.
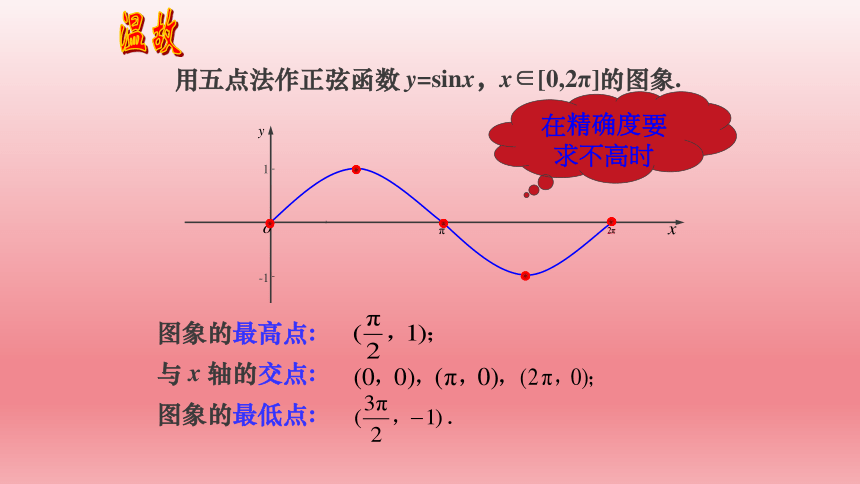
与 x 轴的交点:
图象的最高点:
图象的最低点:
用五点法作正弦函数 y=sinx,x∈[0,2π]的图象.
-
-
-1
1
-
在精确度要求不高时
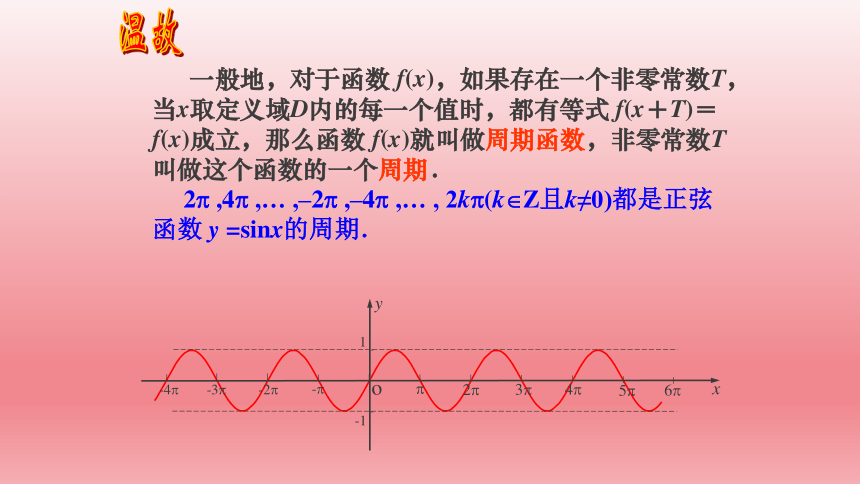
一般地,对于函数 f(x),如果存在一个非零常数T,当x取定义域D内的每一个值时,都有等式 f(x+T)=f(x)成立,那么函数 f(x)就叫做周期函数,非零常数T 叫做这个函数的一个周期.
2 ,4 ,… ,–2 ,–4 ,… , 2k (k Z且k≠0)都是正弦函数 y =sinx的周期.
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
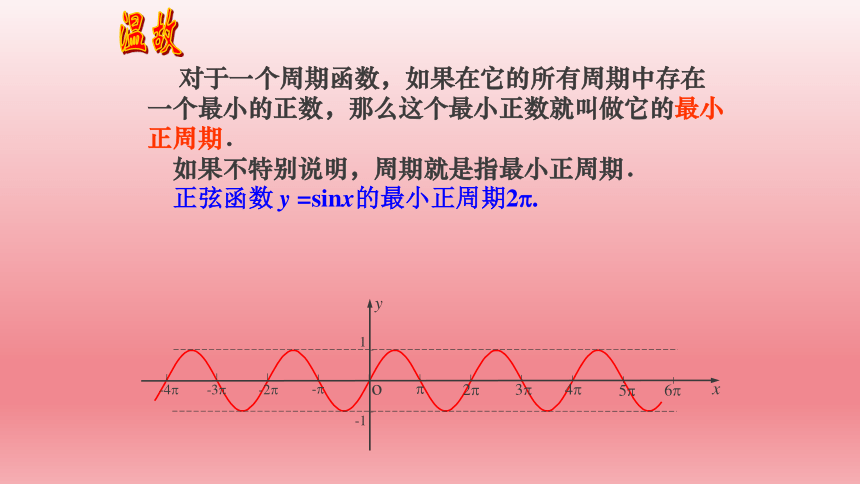
对于一个周期函数,如果在它的所有周期中存在一个最小的正数,那么这个最小正数就叫做它的最小正周期.
如果不特别说明,周期就是指最小正周期.
正弦函数 y =sinx的最小正周期2 .
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
函数 y =sinx
定义域
值域
取得最大值时x的取值集合
取得最小值时x的取值集合
周期
奇偶性
单调增区间
单调减区间
R
[-1,1]
2π
奇函数
我们还知道,
正弦交流电的电压u与时间t之间的关系为 u=Usin( t + )
y = Asin( x+ )
正弦型函数
y=Rsin( t + )
正弦型函数 y=sinx 的图象
正弦型函数 y=2sin x 的图象
正弦型函数 y=sin2 x 的图象
正弦型函数 y=sin(x + )的图象
正弦型函数 y=Asin( x + )的图象
例3:已知函数 ,
求函数取得最小值和最大值时x的取值集合。
3、 ,最大值为 ,最小正周期 ,
初相位 ,求函数解析式。
函数 y=Asin( x + )
振幅
角速度
初相位
定义域
最值
y取最大值时的x
y取最小值时的x
周期
R
ymax=A,ymin=–A
A
§15 三角函数及其应用
3.1正弦型函数的概念
cos( - )=cos ·cos +sin ·sin
两角和(差)的余弦公式
cos( + )=cos ·cos -sin ·sin
两角差的正弦公式
sin( + )=sin ·cos +cos ·sin
sin( - )=sin ·cos -cos ·sin
公式中的 、 可以是任意角.
两角和(差)的正切公式
公式中的 、 、 + 、 - 都不等于 .
sin2 =2sin ·cos
二倍角的正弦公式
cos2 =cos2 -sin2
或 cos2 =2cos2 -1
或 cos2 =1-2sin2
二倍角的余弦公式
公式中的 可以是任意角.
与 x 轴的交点:
图象的最高点:
图象的最低点:
用五点法作正弦函数 y=sinx,x∈[0,2π]的图象.
-
-
-1
1
-
在精确度要求不高时
一般地,对于函数 f(x),如果存在一个非零常数T,当x取定义域D内的每一个值时,都有等式 f(x+T)=f(x)成立,那么函数 f(x)就叫做周期函数,非零常数T 叫做这个函数的一个周期.
2 ,4 ,… ,–2 ,–4 ,… , 2k (k Z且k≠0)都是正弦函数 y =sinx的周期.
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
对于一个周期函数,如果在它的所有周期中存在一个最小的正数,那么这个最小正数就叫做它的最小正周期.
如果不特别说明,周期就是指最小正周期.
正弦函数 y =sinx的最小正周期2 .
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
函数 y =sinx
定义域
值域
取得最大值时x的取值集合
取得最小值时x的取值集合
周期
奇偶性
单调增区间
单调减区间
R
[-1,1]
2π
奇函数
我们还知道,
正弦交流电的电压u与时间t之间的关系为 u=Usin( t + )
y = Asin( x+ )
正弦型函数
y=Rsin( t + )
正弦型函数 y=sinx 的图象
正弦型函数 y=2sin x 的图象
正弦型函数 y=sin2 x 的图象
正弦型函数 y=sin(x + )的图象
正弦型函数 y=Asin( x + )的图象
例3:已知函数 ,
求函数取得最小值和最大值时x的取值集合。
3、 ,最大值为 ,最小正周期 ,
初相位 ,求函数解析式。
函数 y=Asin( x + )
振幅
角速度
初相位
定义域
最值
y取最大值时的x
y取最小值时的x
周期
R
ymax=A,ymin=–A
A
