黑龙江省虎林市八五六农场学校2021-2022学年九年级上学期数学期末考试试题(word版含答案)
文档属性
| 名称 | 黑龙江省虎林市八五六农场学校2021-2022学年九年级上学期数学期末考试试题(word版含答案) | 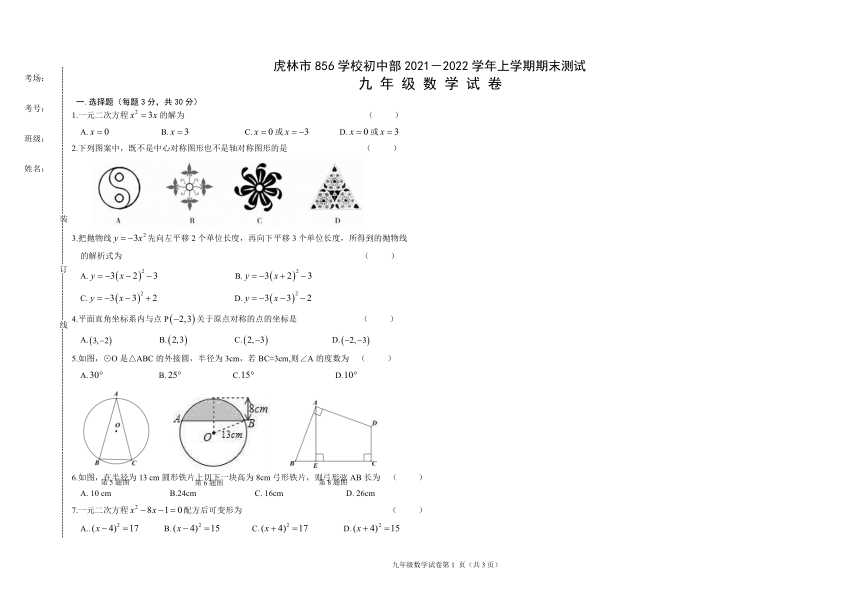 | |
| 格式 | zip | ||
| 文件大小 | 720.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-31 20:32:26 | ||
图片预览


文档简介
虎林市856学校初中部2021-2022学年上学期期末测试
九 年 级 数 学 试 卷
一.选择题(每题3分,共30分)
1.一元二次方程的解为 ( )
A. B. C.或 D.或
2.下列图案中,既不是中心对称图形也不是轴对称图形的是 ( )
3.把抛物线先向左平移2个单位长度,再向下平移3个单位长度,所得到的抛物线
的解析式为 ( )
A. B.
C. D.
4.平面直角坐标系内与点P关于原点对称的点的坐标是 ( )
A. B. C. D.
5.如图,⊙O是△ABC的外接圆,半径为3cm,若BC=3cm,则∠A的度数为 ( )
A. B. C. D.
6.如图,在半径为13 cm圆形铁片上切下一块高为8cm弓形铁片,则弓形弦AB长为 ( )
A. 10 cm B.24cm C. 16cm D. 26cm
7.一元二次方程配方后可变形为 ( )
A.. B. C. D.
8.如图,四边形ABCD中,∠BAD=∠C=90°,AB=AD,AE⊥BC,垂足是E,若线段AE=4,
则四边形ABCD的面积为 ( )
A.12 B.16 C.20 D.24
9.若关于的一元二次方程有实数根,则的取值范围为 ( )
A. B.且
C.且 D.
10. 抛物线对称轴为,与轴的负半轴的交点坐标是,且,它的部分图象如图所示,有下列结论:
① ; ②;
③ ; ④.
其中正确的结论 ( )
A.个 B.个 C.个 D.个
二.填空题(每题3分,共30分)
11. 一个不透明的盒子中装有6个红球,3个黄球和1个绿球,这些球除了颜色外无差别,从中随机摸出一个小球,则摸到的是红球的概率为 .
12. 抛物线的对称轴为 .
13. 一个扇形的圆心角为60°,它所对的弧长为cm,则这个扇形的半径为 cm.
14. 设 m 是一元二次方程x2﹣x﹣2021=0的一个根,则m2﹣m+1的值为 .
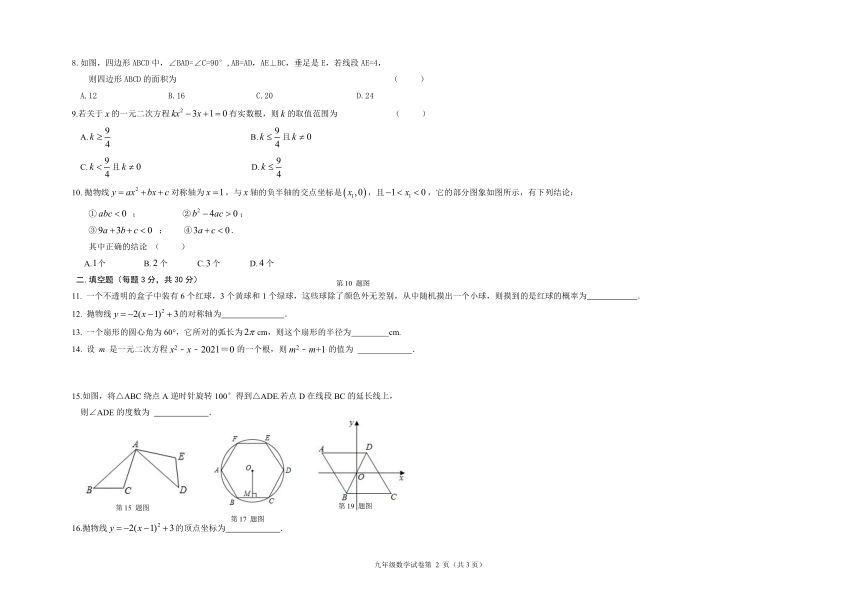
15.如图,将△ABC绕点A逆时针旋转100°得到△ADE.若点D在线段BC的延长线上,
则∠ADE的度数为 .
16.抛物线的顶点坐标为 .
17.如图,正六边形ABCDEF内接于⊙O,半径为4,则它的边心距 OM 长为 .
18.鸡瘟是一种传播速度很快的传染病,一轮传染为一天时间,某养鸡场于某日发现一例,两天后发
现共有169只鸡患有这种病.若每例病鸡传染健康鸡的只数均为x只,则可列方程为
.
19.如图,在平面直角坐标系中,O是菱形ABCD对角线BD的中点,AD∥x轴,AD=4,∠A=60°.
将菱形ABCD绕点O旋转,使点D落在x轴上,则旋转后点C的对应点的坐标是 .
20.如图,在平面直角坐标系中,第1次将边长为1的正方形OABC绕点O逆时针旋转45°后,得到正方形;第2次将正方形绕点O
逆时针旋转45°后, 得到正方形;……;
按此规律,绕点O旋转得到正方形,
则点的坐标为 .
三.解答题(共60分)
21.(8分)有一面积为150平方米的矩形鸡场,鸡场的一边靠墙(墙长18米),另三边用竹篱笆围成,如果竹篱笆的长为35米.求鸡场的长和宽.
22.(8分)一个不透明的布袋里装有2个白球,1个黑球和若干个红球,它们除颜色外其余都相同,
从中任意摸出1个球,是白球的概率为.
(1)布袋里红球有 个.
(2)先从布袋中摸出1个球后不放回,再摸出1个球,请用列表或画树状图等方法求出两次摸到的球都是白球的概率.
23.(8分)如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系中,
△OAB的三个顶点O(0,0)、A(4,1)、B(4,4)均在格点上.
(1)画出△OAB关于y轴对称的,并写出点的坐标;
(2)画出△OAB绕原点O顺时针旋转90°后得到的,并写出点的坐标;
(3)在(2)的条件下,求线段在旋转过程中扫过的面积(结果保留).
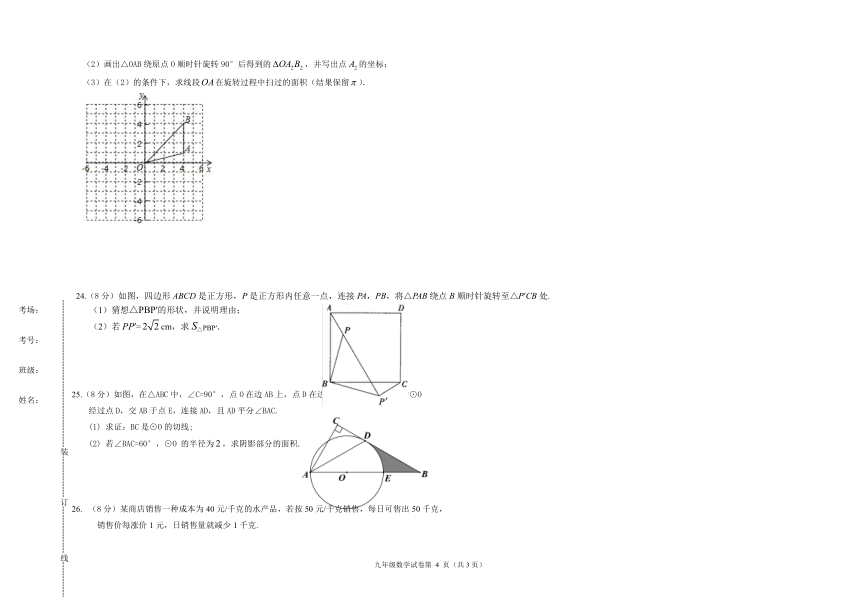
24.(8分)如图,四边形ABCD是正方形,P是正方形内任意一点,连接PA,PB,将△PAB绕点B顺时针旋转至△P′CB处.
(1)猜想△PBP′的形状,并说明理由;
(2)若PP′=cm,求S△PBP′.
25.(8分)如图,在△ABC中,∠C=90°,点O在边AB上,点D在边BC上,以OA为半径的⊙O
经过点D,交AB于点E,连接AD,且AD平分∠BAC.
(1) 求证:BC是⊙O的切线;
(2) 若∠BAC=60°,⊙O 的半径为,求阴影部分的面积.
26. (8分)某商店销售一种成本为40元/千克的水产品,若按50元/千克销售,每日可售出50千克,
销售价每涨价1元,日销售量就减少1千克.
(1)请你直接写出日销售利润(元)与售价(元/千克)之间的函数关系式.
(2)若每日销售利润达到800元,售价应定为多少元?
(3)当售价定为多少元时,这种水产品的日销售利润最大?最大利润是多少元.
27.(12分)如图,已知点B(3,0)、C(0,-3),经过B、C两点的抛物线与轴的
另一个交点为A.
(1)求抛物线的解析式;
(2)点D在抛物线的对称轴上,当△ACD的周长最小时,求点D的坐标;
(3)已知点E在第四象限的抛物线上,过点E作EF∥轴交线段BC于点F,连结EC,若点E,
请直接写出△FEC的面积;
(4)在(3)的条件下,在坐标平面内是否存在点P,使以点A、B、E、P为顶点的四边形是平行
四边形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
九年级数学试卷答案
一.选择题(每题3分,共30分)
1.D 2.C 3.B 4.C 5.A
6.B 7.A 8.B 9.B 10.D
二.填空题(每题3分,共30分)
11. 12. 13. 6 14.2022 15.40° 16.(1,3)
17. 18. 19.或 20.(-1,-1)
三.解答题(共60分)
21.(8分)
解:设垂直于墙的一边长为米,则另一边长为米.
--------------3分
解得:或 --------------3分
当时,,符合题意;
当时,,不符合题意,舍去; - ----1分
答:鸡场的长为15米、宽为10米. - ----1分
22.(8分)
解:
(1)布袋里红球有 1 个. ---------3分
(2) 画树状图如下:
---------2分
∵两次摸球共有12种等可能结果.
∴两次摸到的球都是白球的概率为=. ---------3分
23.(8分)
解:(1)如右图所示, ----2分
点A1的坐标是(﹣4,1); ----1分
(2)如右图所示, ----2分
点A2的坐标是(1,﹣4); ----1分
(3)∵点A(4,1),
∴OA=,
∴线段OA在旋转过程中扫过的面积是:=. ----2分
24.(8分)
解:(1)△PBP′是等腰直角三角形. ----3分
证明:
∵△PAB绕点B顺时针旋转至△P′CB
∴BP′=BP,∠CBP′=∠ABP. ----1分
∵四边形ABCD是正方形,所以∠ABC=90°
∴∠ABP+∠PBC=90°.
∴∠CBP′+∠PBC=90°,即∠PBP′=90° ----1分
∴△PBP′是等腰直角三角形.
(2)因为PP′=cm,所以点B到PP′的距离为PP′=×=(cm).
所以S△PBP′=××=2(cm). ----3分
25.(8分)
(1)证明:连结OD
∵OA=OD
∴∠OAD=∠ODA
又 AD平分∠BAC
∴∠CAD=∠ODA
∴OD∥AC ----2分
∴∠ODB=∠C=90° ----1分
∴OD⊥BC
∴BC是⊙O的切线 ----2分
(2)解:在Rt△ABC中, 由∠C=90°,∠BAC=60°, 得∠B=30°
∴BD=OD= ----1分
又由OD∥AC、得∠EOD=∠BAC=60°
∴ ----2分
26.(8分)
解:(1) ----2分
(2)当时,由得
----2分
解得
故售价应定为每千克60元或每千克80元 ----1分
(3)∵= ----1分
又由可知抛物线的开口向下
∴当时, =900 ----1分
故当售价定为每千克70元时,这种水产品的日销售利润最大,
最大利润是900元 ----1分.
27.(12分)
解:(1)把B(3,0)、C(0,-3)代入抛物线
得 ----1分
解得 ----1分
∴抛物线的解析式为 ----1分
(2) 由可知对称轴为
又点A、B关于对称,
∴ 连结BC与对称轴为的交点就是符合条件的点D
设直线BC的解析式为,则由B(3,0),C(0,-3) 得
解得 ∴ ----2分
当时,
故点D的坐标为(1,-2) ----2分
(3)2 ----2分
(4)存在,、、 ---各1分,共3分.
-----------------------------------------------------装---------------订-----------------线---------------------------------------------------------------------------
考场:
考号:
班级:
姓名:
第5题图
第6题图
第8题图
第10 题图
第17 题图
第19 题图
第15 题图
第20 题图
-----------------------------------------------------装---------------订-----------------线---------------------------------------------------------------------------
考场:
考号:
班级:
姓名:
九 年 级 数 学 试 卷
一.选择题(每题3分,共30分)
1.一元二次方程的解为 ( )
A. B. C.或 D.或
2.下列图案中,既不是中心对称图形也不是轴对称图形的是 ( )
3.把抛物线先向左平移2个单位长度,再向下平移3个单位长度,所得到的抛物线
的解析式为 ( )
A. B.
C. D.
4.平面直角坐标系内与点P关于原点对称的点的坐标是 ( )
A. B. C. D.
5.如图,⊙O是△ABC的外接圆,半径为3cm,若BC=3cm,则∠A的度数为 ( )
A. B. C. D.
6.如图,在半径为13 cm圆形铁片上切下一块高为8cm弓形铁片,则弓形弦AB长为 ( )
A. 10 cm B.24cm C. 16cm D. 26cm
7.一元二次方程配方后可变形为 ( )
A.. B. C. D.
8.如图,四边形ABCD中,∠BAD=∠C=90°,AB=AD,AE⊥BC,垂足是E,若线段AE=4,
则四边形ABCD的面积为 ( )
A.12 B.16 C.20 D.24
9.若关于的一元二次方程有实数根,则的取值范围为 ( )
A. B.且
C.且 D.
10. 抛物线对称轴为,与轴的负半轴的交点坐标是,且,它的部分图象如图所示,有下列结论:
① ; ②;
③ ; ④.
其中正确的结论 ( )
A.个 B.个 C.个 D.个
二.填空题(每题3分,共30分)
11. 一个不透明的盒子中装有6个红球,3个黄球和1个绿球,这些球除了颜色外无差别,从中随机摸出一个小球,则摸到的是红球的概率为 .
12. 抛物线的对称轴为 .
13. 一个扇形的圆心角为60°,它所对的弧长为cm,则这个扇形的半径为 cm.
14. 设 m 是一元二次方程x2﹣x﹣2021=0的一个根,则m2﹣m+1的值为 .
15.如图,将△ABC绕点A逆时针旋转100°得到△ADE.若点D在线段BC的延长线上,
则∠ADE的度数为 .
16.抛物线的顶点坐标为 .
17.如图,正六边形ABCDEF内接于⊙O,半径为4,则它的边心距 OM 长为 .
18.鸡瘟是一种传播速度很快的传染病,一轮传染为一天时间,某养鸡场于某日发现一例,两天后发
现共有169只鸡患有这种病.若每例病鸡传染健康鸡的只数均为x只,则可列方程为
.
19.如图,在平面直角坐标系中,O是菱形ABCD对角线BD的中点,AD∥x轴,AD=4,∠A=60°.
将菱形ABCD绕点O旋转,使点D落在x轴上,则旋转后点C的对应点的坐标是 .
20.如图,在平面直角坐标系中,第1次将边长为1的正方形OABC绕点O逆时针旋转45°后,得到正方形;第2次将正方形绕点O
逆时针旋转45°后, 得到正方形;……;
按此规律,绕点O旋转得到正方形,
则点的坐标为 .
三.解答题(共60分)
21.(8分)有一面积为150平方米的矩形鸡场,鸡场的一边靠墙(墙长18米),另三边用竹篱笆围成,如果竹篱笆的长为35米.求鸡场的长和宽.
22.(8分)一个不透明的布袋里装有2个白球,1个黑球和若干个红球,它们除颜色外其余都相同,
从中任意摸出1个球,是白球的概率为.
(1)布袋里红球有 个.
(2)先从布袋中摸出1个球后不放回,再摸出1个球,请用列表或画树状图等方法求出两次摸到的球都是白球的概率.
23.(8分)如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系中,
△OAB的三个顶点O(0,0)、A(4,1)、B(4,4)均在格点上.
(1)画出△OAB关于y轴对称的,并写出点的坐标;
(2)画出△OAB绕原点O顺时针旋转90°后得到的,并写出点的坐标;
(3)在(2)的条件下,求线段在旋转过程中扫过的面积(结果保留).
24.(8分)如图,四边形ABCD是正方形,P是正方形内任意一点,连接PA,PB,将△PAB绕点B顺时针旋转至△P′CB处.
(1)猜想△PBP′的形状,并说明理由;
(2)若PP′=cm,求S△PBP′.
25.(8分)如图,在△ABC中,∠C=90°,点O在边AB上,点D在边BC上,以OA为半径的⊙O
经过点D,交AB于点E,连接AD,且AD平分∠BAC.
(1) 求证:BC是⊙O的切线;
(2) 若∠BAC=60°,⊙O 的半径为,求阴影部分的面积.
26. (8分)某商店销售一种成本为40元/千克的水产品,若按50元/千克销售,每日可售出50千克,
销售价每涨价1元,日销售量就减少1千克.
(1)请你直接写出日销售利润(元)与售价(元/千克)之间的函数关系式.
(2)若每日销售利润达到800元,售价应定为多少元?
(3)当售价定为多少元时,这种水产品的日销售利润最大?最大利润是多少元.
27.(12分)如图,已知点B(3,0)、C(0,-3),经过B、C两点的抛物线与轴的
另一个交点为A.
(1)求抛物线的解析式;
(2)点D在抛物线的对称轴上,当△ACD的周长最小时,求点D的坐标;
(3)已知点E在第四象限的抛物线上,过点E作EF∥轴交线段BC于点F,连结EC,若点E,
请直接写出△FEC的面积;
(4)在(3)的条件下,在坐标平面内是否存在点P,使以点A、B、E、P为顶点的四边形是平行
四边形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
九年级数学试卷答案
一.选择题(每题3分,共30分)
1.D 2.C 3.B 4.C 5.A
6.B 7.A 8.B 9.B 10.D
二.填空题(每题3分,共30分)
11. 12. 13. 6 14.2022 15.40° 16.(1,3)
17. 18. 19.或 20.(-1,-1)
三.解答题(共60分)
21.(8分)
解:设垂直于墙的一边长为米,则另一边长为米.
--------------3分
解得:或 --------------3分
当时,,符合题意;
当时,,不符合题意,舍去; - ----1分
答:鸡场的长为15米、宽为10米. - ----1分
22.(8分)
解:
(1)布袋里红球有 1 个. ---------3分
(2) 画树状图如下:
---------2分
∵两次摸球共有12种等可能结果.
∴两次摸到的球都是白球的概率为=. ---------3分
23.(8分)
解:(1)如右图所示, ----2分
点A1的坐标是(﹣4,1); ----1分
(2)如右图所示, ----2分
点A2的坐标是(1,﹣4); ----1分
(3)∵点A(4,1),
∴OA=,
∴线段OA在旋转过程中扫过的面积是:=. ----2分
24.(8分)
解:(1)△PBP′是等腰直角三角形. ----3分
证明:
∵△PAB绕点B顺时针旋转至△P′CB
∴BP′=BP,∠CBP′=∠ABP. ----1分
∵四边形ABCD是正方形,所以∠ABC=90°
∴∠ABP+∠PBC=90°.
∴∠CBP′+∠PBC=90°,即∠PBP′=90° ----1分
∴△PBP′是等腰直角三角形.
(2)因为PP′=cm,所以点B到PP′的距离为PP′=×=(cm).
所以S△PBP′=××=2(cm). ----3分
25.(8分)
(1)证明:连结OD
∵OA=OD
∴∠OAD=∠ODA
又 AD平分∠BAC
∴∠CAD=∠ODA
∴OD∥AC ----2分
∴∠ODB=∠C=90° ----1分
∴OD⊥BC
∴BC是⊙O的切线 ----2分
(2)解:在Rt△ABC中, 由∠C=90°,∠BAC=60°, 得∠B=30°
∴BD=OD= ----1分
又由OD∥AC、得∠EOD=∠BAC=60°
∴ ----2分
26.(8分)
解:(1) ----2分
(2)当时,由得
----2分
解得
故售价应定为每千克60元或每千克80元 ----1分
(3)∵= ----1分
又由可知抛物线的开口向下
∴当时, =900 ----1分
故当售价定为每千克70元时,这种水产品的日销售利润最大,
最大利润是900元 ----1分.
27.(12分)
解:(1)把B(3,0)、C(0,-3)代入抛物线
得 ----1分
解得 ----1分
∴抛物线的解析式为 ----1分
(2) 由可知对称轴为
又点A、B关于对称,
∴ 连结BC与对称轴为的交点就是符合条件的点D
设直线BC的解析式为,则由B(3,0),C(0,-3) 得
解得 ∴ ----2分
当时,
故点D的坐标为(1,-2) ----2分
(3)2 ----2分
(4)存在,、、 ---各1分,共3分.
-----------------------------------------------------装---------------订-----------------线---------------------------------------------------------------------------
考场:
考号:
班级:
姓名:
第5题图
第6题图
第8题图
第10 题图
第17 题图
第19 题图
第15 题图
第20 题图
-----------------------------------------------------装---------------订-----------------线---------------------------------------------------------------------------
考场:
考号:
班级:
姓名:
同课章节目录
