黑龙江省密山市兴凯湖农场学校2021-2022学年八年级上学期数学期末考试试题(word版含答案)
文档属性
| 名称 | 黑龙江省密山市兴凯湖农场学校2021-2022学年八年级上学期数学期末考试试题(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 277.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-31 00:00:00 | ||
图片预览



文档简介
八年级数学期末试卷
考生注意:
1.考试时间90分钟
2.全卷共三道大题,总分120分
题号 一 二 三 总 分 核分人
21 22 23 24 25 26 27 28
得分
得分 评卷人
1、选择题(每小题3分,满分30分)
1.下列计算中,正确的是 ( )
A. B. C. D.
2.在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是 ( )
3.三角形的三边长分别为5,8,x,则最长边x的取值范围是 ( )
A.3<x<8 B.5<x<13 C.3<x<13 D.8<x<13
4..下列因式分解正确的是 ( )
A.16m2-4=(4m+2)(4m-2) B.m4-1=(m2+1)(m2-1)
C.m2-6m+9=(m-3)2 D.1-a2=(a+1)(a-1)
5一个多边形切去一个角后,形成的另一个多边形的内角和为1080°,那么
原多边形的边数为 ( )
A. 7 B. 7或8 C. 8或9 D. 7或8或9
6.若关于x的方程+=3的解为正数,则m的取值范围是 ( )
A.m< B.m<且m≠ C.m>- D.m>-且m≠-
7. 如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于E,垂足为D.
如果CE=12,则ED的长为 A.3 B.4 C.5 D.6 ( )
8.如图△ABC中,∠A=96°,延长BC到D,∠ABC与∠ACD的平分线相交于点A1,
∠A1BC与∠A1CD的平分线相交于点A2,依此类推,∠A4BC与∠A4CD的平分线
相交于点A5,则∠A5的度数为 ( )
A.19.2° B.8° C.6° D 3°.
9.如图,OP平分∠BOA,PC⊥OA,PD⊥OB,垂足分别是C、D,则下列结论中
错误的是 ( )
A.PC=PD B.OC=OD C.OC=OP D.∠CPO=∠DPO
10.如图,是四边形ABCD的对称轴,AD∥BC,现给出 下列结论:
①AB∥CD;②AB=BC;③AB⊥BC;④AO=OC 其中正确的结论有 ( )
A:1个 B:2个 C:3个 D:4个
二、填空题(每小题3分,满分30分)
11. 人体中红细胞的直径约为0.0000077m,将数0.0000077用科学记数法
表示 为 .
12.若分式有意义,则x应满足的条件是________.
13.已知等腰三角形的其中两边长分别为4,9,则这个等腰三角形的周长为
.
14. 如果分式的值为零,那么x= .
15. 若16b2+a2+m是完全平方式,则m= .
16.3m=4,3n=6,则3m+2n=__ .
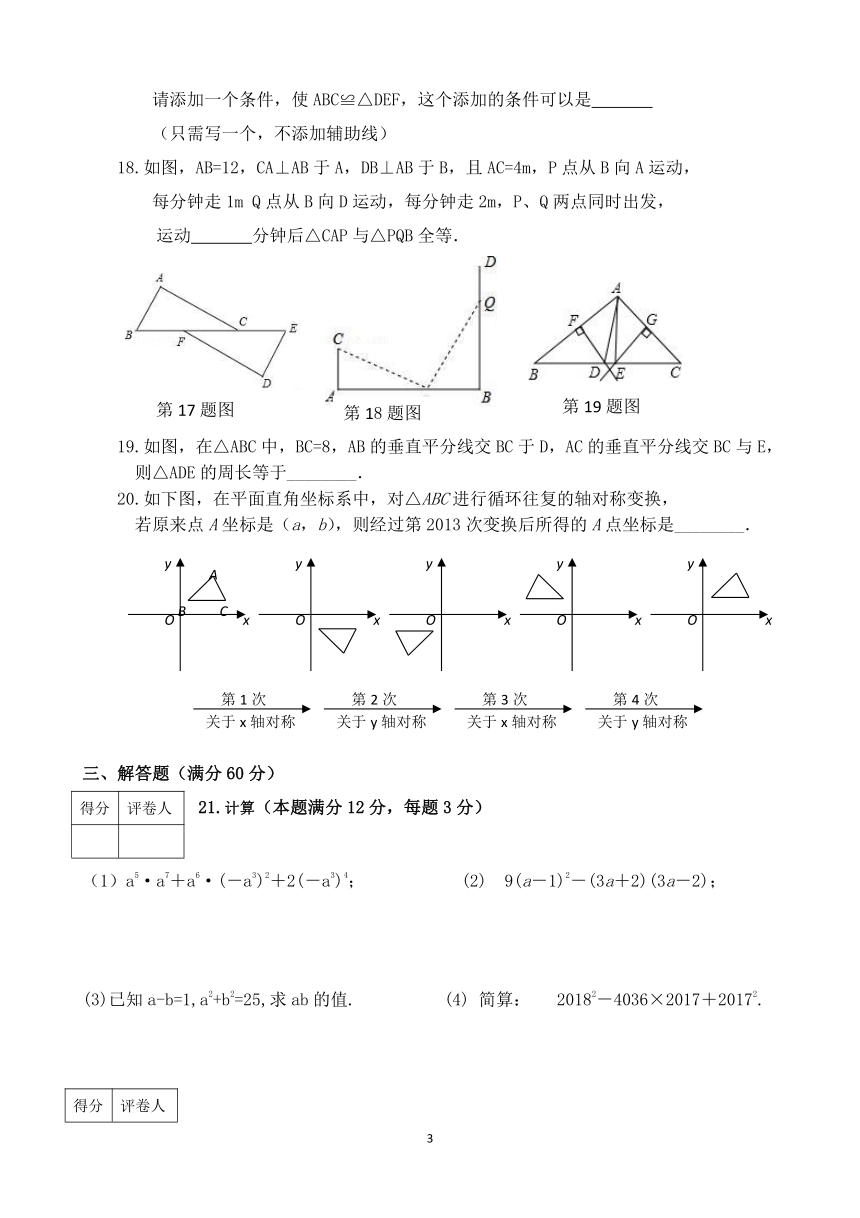
17.如图,在△ABC和△DEF中,点B,F,C,E在同一直线上,BF=CE,AB∥DE,
请添加一个条件,使ABC≌△DEF,这个添加的条件可以是
(只需写一个,不添加辅助线)
18. 如图,AB=12,CA⊥AB于A,DB⊥AB于B,且AC=4m,P点从B向A运动,
每分钟走1m Q点从B向D运动,每分钟走2m,P、Q两点同时出发,
运动 分钟后△CAP与△PQB全等.
19.如图,在△ABC中,BC=8,AB的垂直平分线交BC于D,AC的垂直平分线交BC与E,
则△ADE的周长等于________.
20.如下图,在平面直角坐标系中,对△ABC进行循环往复的轴对称变换,
若原来点A坐标是(a,b),则经过第2013次变换后所得的A点坐标是________.
三、解答题(满分60分)
得分 评卷人
21.计算(本题满分12分,每题3分)
(1)a5·a7+a6·(-a3)2+2(-a3)4; (2) 9(a-1)2-(3a+2)(3a-2);
(3)已知a-b=1,a2+b2=25,求ab的值. (4) 简算: 20182-4036×2017+20172.
得分 评卷人
22.(本题满分6分)
先阅读下列材料:
我们已经学过将一个多项式分解因式的方法有提公因式法和运用公式法,其实分解因式的方法还有分组分解法、拆项法、十字相乘法等等.
拆项法:将一个多项式的某一项拆成两项后,可提公因式或运用公式继续分解的方法.如:
x2+2x﹣3=x2+2x+1﹣4=(x+1)2﹣22=(x+1+2)(x+1﹣2)=(x+3)(x﹣1)
请你仿照以上方法,探索并解决下列问题:
(1)分解因式:x2﹣6x﹣7;
(2)分解因式:a2+4ab﹣5b2.
得分 评卷人
23.(本题满分6分)
先化简求值:,其中x=3.
24.(本题满分6分)
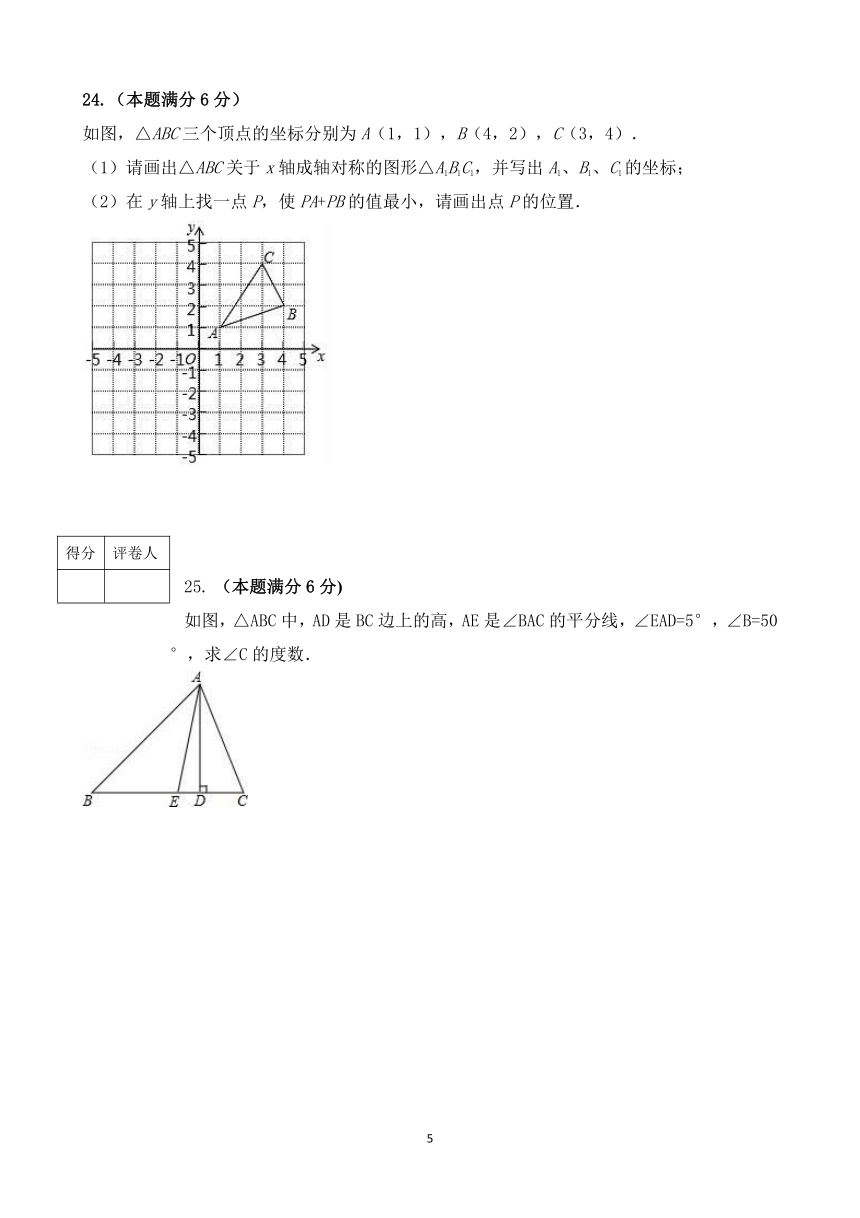
如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)请画出△ABC关于x轴成轴对称的图形△A1B1C1,并写出A1、B1、C1的坐标;
(2)在y轴上找一点P,使PA+PB的值最小,请画出点P的位置.
得分 评卷人
25. (本题满分6分)
如图,△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠EAD=5°,∠B=50°,求∠C的度数.
得分 评卷人
26.(本题满分8分)
虎林西苑社区在扎实开展党史学习教育期间,开展“我为群众办实事”活动,为某小区铺设一段全长为720米的排污管道,为减少施工对居民生活的影响,须缩短施工时间,实际施工时每天铺设管道的长度是原计划的1.2倍,结果提前2天完成任务,求原计划每天铺设管道的长度.
得分 评卷人
27.(本题满分8分)
.如图,在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于D,CE⊥DE于点E;
(1)若B、C在DE的同侧(如图所示)且AD=CE.求证:AB⊥AC;
(2)若B、C在DE的两侧(如图所示),其他条件不变,AB与AC仍垂直吗?若是请给出证明;若不是,请说明理由.
得分 评卷人
28.(本题满分8分))
如图,在平面直角坐标系中,O为坐标原点,A、B两点的坐标分别为A(0,m)、B(n,0),且|m﹣n﹣3|+=0,点P从A出发,以每秒1个单位的速度沿射线AO匀速运动,设点P的运动时间为t秒.
(1)求OA、OB的长;
(2)连接PB,设△POB的面积为S,用t的式子表示S;
(3)过点P作直线AB的垂线,垂足为D,直线PD与x轴交于点E,在点P运动的过程中,是否存在这样的点P,使△EOP≌△AOB?若存在,请求出t的值;若不存在,请说明理由.
数学试题参考答案及评分说明
一、单项选择题(每题3分,满分30分)
1 2 3 4 5 6 7 8 9 10
D A D C D B D D C C
二、填空题(每题3分,满分30分)
11 7.7×10-6 12.x≠2 13. 22 14.x=- 1 15.±8ab (对1个得2分,有错不得分) 16. 144 17.AB=ED (答案不唯一,合理即可) 18. 4 19.8 20.(a,-b)
三、解答题(满分60分)
21.(本小题满分12分,每题3分)
(1)解:原式= a12+a12+2a12 ------ (2分) (2)解:原式= 9a2-18a+9-9a2+4 ---(2分)
= 4a12 ------ (1分) =-18a+13 ------ (1分)
(3)解∵a-b=1,∴(a-b)2=a2+b2-2ab=1 ------ (2分) (4)解:原式=(2018-2017)2 ------ (2分)
∵a2+b2=25,∴25-2ab=1,解得ab=12. ------ (1分) =1 ------ (1分)
22(本小题满分6分)
解:(1)原式=(x﹣7)(x+1);-------------------- (3分)
(2)原式=(a﹣b)(a+5b).-------------------- (3分)
23(本小题满分6分)
解:原式= ﹣ ------ (2分)
=﹣ ------ (2分)
=, ------ (1分) 当x=3时,原式=. ------ (1分)
24(本小题满分6分)解:
(1)如图所示,△A1B1C1即为所求,------ (1分)
A1的坐标为(1,﹣1)、B1的坐标为(4,﹣2)、C1的坐标为(3,﹣4);…………3分
(2)如图所示,点P即为所求.------ (2分)
25. (本题满分6分)
解:∵AD是BC边上的高,∠EAD=5°,∴∠AED=85°,
∵∠B=50°,∴∠BAE=∠AED﹣∠B=85°﹣50°=35°,------ (2分)
∵AE是∠BAC的角平分线,∴∠BAC=2∠BAE=70°,------ (2分)
∴∠C=180°﹣∠B﹣∠BAC=180°﹣50°﹣70°=60°------ (2分)
26.(本小题满分8分)
解:设原计划每天铺设管道x米. ------ (1分)
由题意,得. ------ (4分)
解得x=60. ------ (1分)
经检验,x=60是原方程的解.且符合题意. ------ (1分)
答:原计划每天铺设管道60米. ------ (1分)
27.(本小题满分8分)
解:(1)证明:∵BD⊥DE,CE⊥DE,∴∠ADB=∠AEC=90°, ------ (1分)
在Rt△ABD和Rt△ACE中,∵,∴Rt△ABD≌Rt△CAE.
∴∠DAB=∠ECA,∠DBA=∠ACE. ------ (2分)
∵∠DAB+∠DBA=90°,∠EAC+∠ACE=90°,
∴∠BAD+∠CAE=90°.∠BAC=180°﹣(∠BAD+∠CAE)=90°.
∴AB⊥AC. ------ (2分)
(2)AB⊥AC. ------ (1分)理由如下:
同(1)一样可证得Rt△ABD≌Rt△ACE.∴∠DAB=∠ECA,∠DBA=∠EAC,
∵∠CAE+∠ECA=90°, ------ (1分)∴∠CAE+∠BAD=90°,即∠BAC=90°,
∴AB⊥AC. ------ (1分)
28(本小题满分8分). 解:(1)∵|m﹣n﹣3|+=0,
且|m﹣n﹣3|≥0,≥0∴|m﹣n﹣3|==0,
∴n=3,m=6,∴点A(0,6),点B(3,0); ------ (2分)
(2)连接PB,
t秒后,AP=t,OP=|6﹣t|,∴S=OP OB=|6﹣t|;(t≥0)------ (2分)
(3)作出图形,
∵∠OAB+∠OBA=90°,∠OAB+∠APD=90°,∠OPE=∠APD,
∴∠OBA=∠OPE,------ (2分)
∴只要OP=OB,即可求证△EOP≌△AOB,∴AP=AO﹣OP=3,或AP′=OA+OP′=9
∴t=3或9.------ (2分)
A
D
C
B
第7题图
第8题图
第9题图
第10题图
第19题图
第17题图
第18题图
y
x
O
A
B
C
y
x
O
y
x
O
y
x
O
y
x
O
第1次
关于x轴对称
第2次
关于y轴对称
第3次
关于x轴对称
第4次
关于y轴对称
28题备用图
考生注意:
1.考试时间90分钟
2.全卷共三道大题,总分120分
题号 一 二 三 总 分 核分人
21 22 23 24 25 26 27 28
得分
得分 评卷人
1、选择题(每小题3分,满分30分)
1.下列计算中,正确的是 ( )
A. B. C. D.
2.在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是 ( )
3.三角形的三边长分别为5,8,x,则最长边x的取值范围是 ( )
A.3<x<8 B.5<x<13 C.3<x<13 D.8<x<13
4..下列因式分解正确的是 ( )
A.16m2-4=(4m+2)(4m-2) B.m4-1=(m2+1)(m2-1)
C.m2-6m+9=(m-3)2 D.1-a2=(a+1)(a-1)
5一个多边形切去一个角后,形成的另一个多边形的内角和为1080°,那么
原多边形的边数为 ( )
A. 7 B. 7或8 C. 8或9 D. 7或8或9
6.若关于x的方程+=3的解为正数,则m的取值范围是 ( )
A.m< B.m<且m≠ C.m>- D.m>-且m≠-
7. 如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于E,垂足为D.
如果CE=12,则ED的长为 A.3 B.4 C.5 D.6 ( )
8.如图△ABC中,∠A=96°,延长BC到D,∠ABC与∠ACD的平分线相交于点A1,
∠A1BC与∠A1CD的平分线相交于点A2,依此类推,∠A4BC与∠A4CD的平分线
相交于点A5,则∠A5的度数为 ( )
A.19.2° B.8° C.6° D 3°.
9.如图,OP平分∠BOA,PC⊥OA,PD⊥OB,垂足分别是C、D,则下列结论中
错误的是 ( )
A.PC=PD B.OC=OD C.OC=OP D.∠CPO=∠DPO
10.如图,是四边形ABCD的对称轴,AD∥BC,现给出 下列结论:
①AB∥CD;②AB=BC;③AB⊥BC;④AO=OC 其中正确的结论有 ( )
A:1个 B:2个 C:3个 D:4个
二、填空题(每小题3分,满分30分)
11. 人体中红细胞的直径约为0.0000077m,将数0.0000077用科学记数法
表示 为 .
12.若分式有意义,则x应满足的条件是________.
13.已知等腰三角形的其中两边长分别为4,9,则这个等腰三角形的周长为
.
14. 如果分式的值为零,那么x= .
15. 若16b2+a2+m是完全平方式,则m= .
16.3m=4,3n=6,则3m+2n=__ .
17.如图,在△ABC和△DEF中,点B,F,C,E在同一直线上,BF=CE,AB∥DE,
请添加一个条件,使ABC≌△DEF,这个添加的条件可以是
(只需写一个,不添加辅助线)
18. 如图,AB=12,CA⊥AB于A,DB⊥AB于B,且AC=4m,P点从B向A运动,
每分钟走1m Q点从B向D运动,每分钟走2m,P、Q两点同时出发,
运动 分钟后△CAP与△PQB全等.
19.如图,在△ABC中,BC=8,AB的垂直平分线交BC于D,AC的垂直平分线交BC与E,
则△ADE的周长等于________.
20.如下图,在平面直角坐标系中,对△ABC进行循环往复的轴对称变换,
若原来点A坐标是(a,b),则经过第2013次变换后所得的A点坐标是________.
三、解答题(满分60分)
得分 评卷人
21.计算(本题满分12分,每题3分)
(1)a5·a7+a6·(-a3)2+2(-a3)4; (2) 9(a-1)2-(3a+2)(3a-2);
(3)已知a-b=1,a2+b2=25,求ab的值. (4) 简算: 20182-4036×2017+20172.
得分 评卷人
22.(本题满分6分)
先阅读下列材料:
我们已经学过将一个多项式分解因式的方法有提公因式法和运用公式法,其实分解因式的方法还有分组分解法、拆项法、十字相乘法等等.
拆项法:将一个多项式的某一项拆成两项后,可提公因式或运用公式继续分解的方法.如:
x2+2x﹣3=x2+2x+1﹣4=(x+1)2﹣22=(x+1+2)(x+1﹣2)=(x+3)(x﹣1)
请你仿照以上方法,探索并解决下列问题:
(1)分解因式:x2﹣6x﹣7;
(2)分解因式:a2+4ab﹣5b2.
得分 评卷人
23.(本题满分6分)
先化简求值:,其中x=3.
24.(本题满分6分)
如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)请画出△ABC关于x轴成轴对称的图形△A1B1C1,并写出A1、B1、C1的坐标;
(2)在y轴上找一点P,使PA+PB的值最小,请画出点P的位置.
得分 评卷人
25. (本题满分6分)
如图,△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠EAD=5°,∠B=50°,求∠C的度数.
得分 评卷人
26.(本题满分8分)
虎林西苑社区在扎实开展党史学习教育期间,开展“我为群众办实事”活动,为某小区铺设一段全长为720米的排污管道,为减少施工对居民生活的影响,须缩短施工时间,实际施工时每天铺设管道的长度是原计划的1.2倍,结果提前2天完成任务,求原计划每天铺设管道的长度.
得分 评卷人
27.(本题满分8分)
.如图,在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于D,CE⊥DE于点E;
(1)若B、C在DE的同侧(如图所示)且AD=CE.求证:AB⊥AC;
(2)若B、C在DE的两侧(如图所示),其他条件不变,AB与AC仍垂直吗?若是请给出证明;若不是,请说明理由.
得分 评卷人
28.(本题满分8分))
如图,在平面直角坐标系中,O为坐标原点,A、B两点的坐标分别为A(0,m)、B(n,0),且|m﹣n﹣3|+=0,点P从A出发,以每秒1个单位的速度沿射线AO匀速运动,设点P的运动时间为t秒.
(1)求OA、OB的长;
(2)连接PB,设△POB的面积为S,用t的式子表示S;
(3)过点P作直线AB的垂线,垂足为D,直线PD与x轴交于点E,在点P运动的过程中,是否存在这样的点P,使△EOP≌△AOB?若存在,请求出t的值;若不存在,请说明理由.
数学试题参考答案及评分说明
一、单项选择题(每题3分,满分30分)
1 2 3 4 5 6 7 8 9 10
D A D C D B D D C C
二、填空题(每题3分,满分30分)
11 7.7×10-6 12.x≠2 13. 22 14.x=- 1 15.±8ab (对1个得2分,有错不得分) 16. 144 17.AB=ED (答案不唯一,合理即可) 18. 4 19.8 20.(a,-b)
三、解答题(满分60分)
21.(本小题满分12分,每题3分)
(1)解:原式= a12+a12+2a12 ------ (2分) (2)解:原式= 9a2-18a+9-9a2+4 ---(2分)
= 4a12 ------ (1分) =-18a+13 ------ (1分)
(3)解∵a-b=1,∴(a-b)2=a2+b2-2ab=1 ------ (2分) (4)解:原式=(2018-2017)2 ------ (2分)
∵a2+b2=25,∴25-2ab=1,解得ab=12. ------ (1分) =1 ------ (1分)
22(本小题满分6分)
解:(1)原式=(x﹣7)(x+1);-------------------- (3分)
(2)原式=(a﹣b)(a+5b).-------------------- (3分)
23(本小题满分6分)
解:原式= ﹣ ------ (2分)
=﹣ ------ (2分)
=, ------ (1分) 当x=3时,原式=. ------ (1分)
24(本小题满分6分)解:
(1)如图所示,△A1B1C1即为所求,------ (1分)
A1的坐标为(1,﹣1)、B1的坐标为(4,﹣2)、C1的坐标为(3,﹣4);…………3分
(2)如图所示,点P即为所求.------ (2分)
25. (本题满分6分)
解:∵AD是BC边上的高,∠EAD=5°,∴∠AED=85°,
∵∠B=50°,∴∠BAE=∠AED﹣∠B=85°﹣50°=35°,------ (2分)
∵AE是∠BAC的角平分线,∴∠BAC=2∠BAE=70°,------ (2分)
∴∠C=180°﹣∠B﹣∠BAC=180°﹣50°﹣70°=60°------ (2分)
26.(本小题满分8分)
解:设原计划每天铺设管道x米. ------ (1分)
由题意,得. ------ (4分)
解得x=60. ------ (1分)
经检验,x=60是原方程的解.且符合题意. ------ (1分)
答:原计划每天铺设管道60米. ------ (1分)
27.(本小题满分8分)
解:(1)证明:∵BD⊥DE,CE⊥DE,∴∠ADB=∠AEC=90°, ------ (1分)
在Rt△ABD和Rt△ACE中,∵,∴Rt△ABD≌Rt△CAE.
∴∠DAB=∠ECA,∠DBA=∠ACE. ------ (2分)
∵∠DAB+∠DBA=90°,∠EAC+∠ACE=90°,
∴∠BAD+∠CAE=90°.∠BAC=180°﹣(∠BAD+∠CAE)=90°.
∴AB⊥AC. ------ (2分)
(2)AB⊥AC. ------ (1分)理由如下:
同(1)一样可证得Rt△ABD≌Rt△ACE.∴∠DAB=∠ECA,∠DBA=∠EAC,
∵∠CAE+∠ECA=90°, ------ (1分)∴∠CAE+∠BAD=90°,即∠BAC=90°,
∴AB⊥AC. ------ (1分)
28(本小题满分8分). 解:(1)∵|m﹣n﹣3|+=0,
且|m﹣n﹣3|≥0,≥0∴|m﹣n﹣3|==0,
∴n=3,m=6,∴点A(0,6),点B(3,0); ------ (2分)
(2)连接PB,
t秒后,AP=t,OP=|6﹣t|,∴S=OP OB=|6﹣t|;(t≥0)------ (2分)
(3)作出图形,
∵∠OAB+∠OBA=90°,∠OAB+∠APD=90°,∠OPE=∠APD,
∴∠OBA=∠OPE,------ (2分)
∴只要OP=OB,即可求证△EOP≌△AOB,∴AP=AO﹣OP=3,或AP′=OA+OP′=9
∴t=3或9.------ (2分)
A
D
C
B
第7题图
第8题图
第9题图
第10题图
第19题图
第17题图
第18题图
y
x
O
A
B
C
y
x
O
y
x
O
y
x
O
y
x
O
第1次
关于x轴对称
第2次
关于y轴对称
第3次
关于x轴对称
第4次
关于y轴对称
28题备用图
同课章节目录
