八年级数学(3)利用勾股定理求作线段
文档属性
| 名称 | 八年级数学(3)利用勾股定理求作线段 |  | |
| 格式 | zip | ||
| 文件大小 | 198.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-02 14:51:32 | ||
图片预览

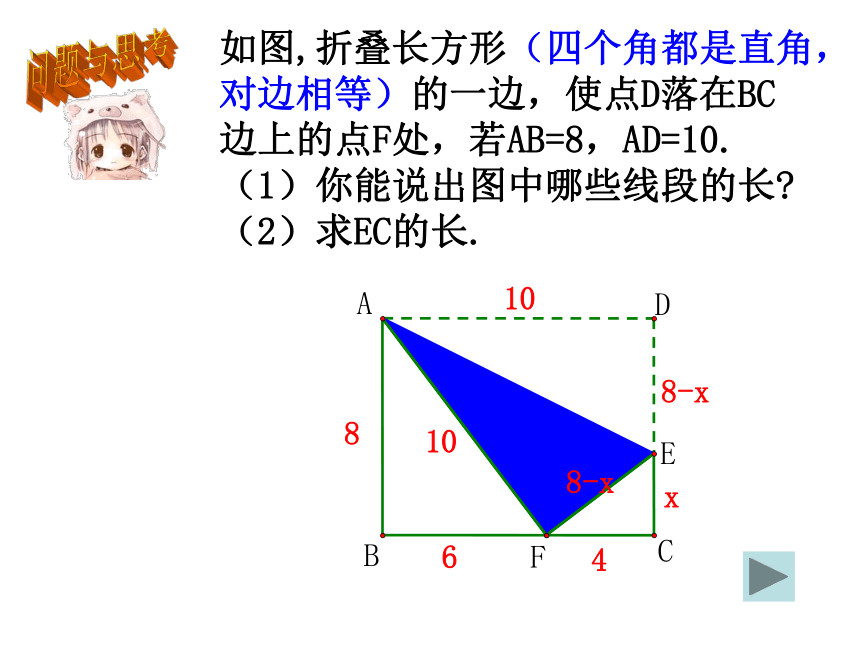
文档简介
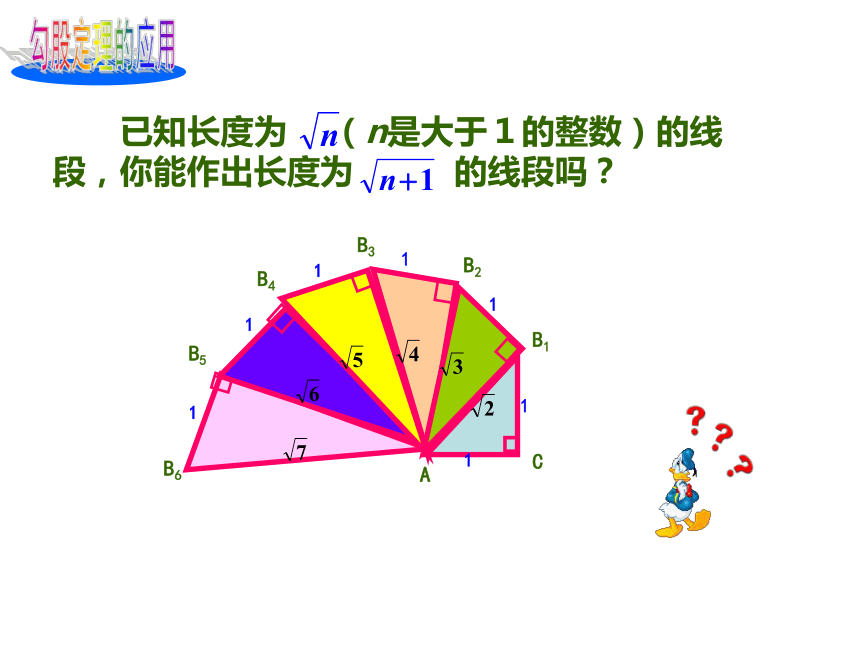
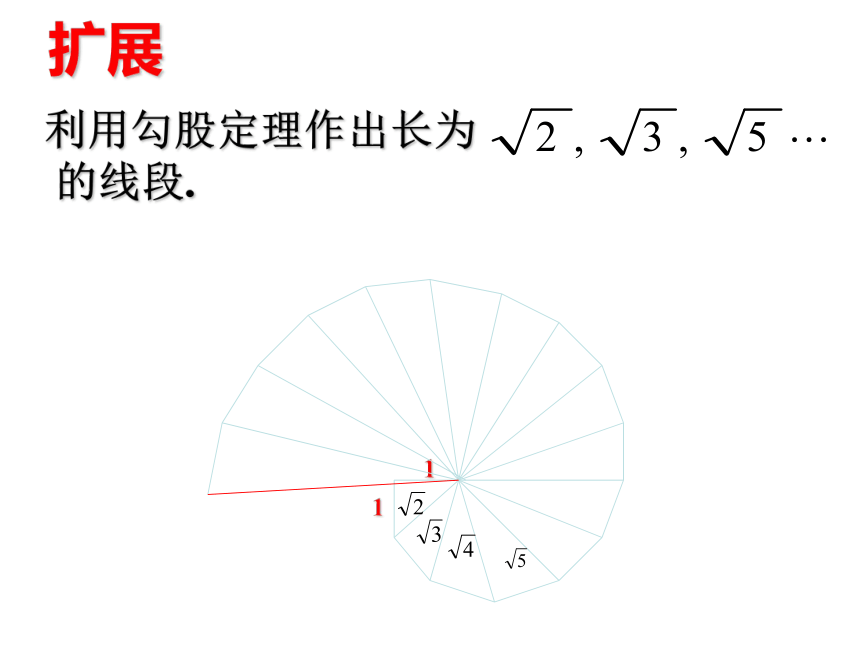
课件12张PPT。勾股定理的应用你能在给出的数轴上找出表示 的点吗? 试一试:012345-2-111你能找出表示 这些数的点吗? 已知长度为 (n是大于1的整数)的线段,你能作出长度为 的线段吗? 勾股定理的应用扩展利用勾股定理作出长为
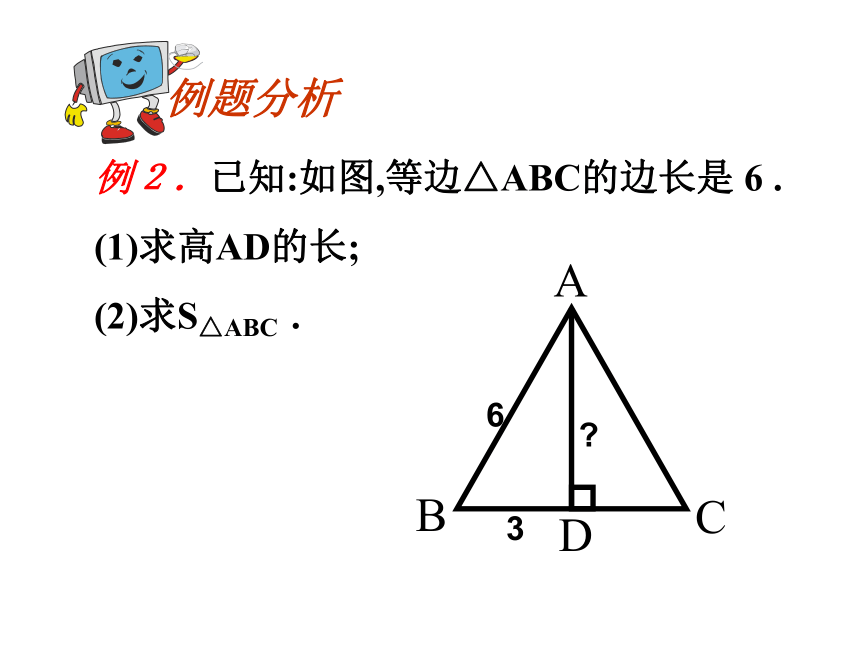
的线段.11 例2.已知:如图,等边△ABC的边长是 6 .
(1)求高AD的长;
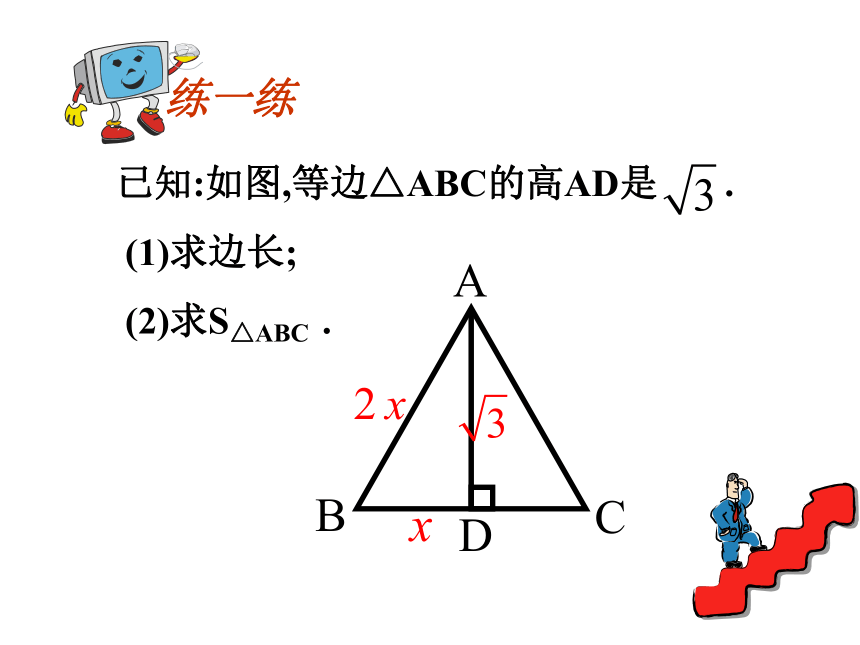
(2)求S△ABC .例题分析36? 已知:如图,等边△ABC的高AD是 .
(1)求边长;
(2)求S△ABC .练一练1046810xEFDCBA8-x8-x10、如图,把长方形纸片ABCD折叠,使顶点A与顶点C重合在一起,EF为折痕。若AB=9,BC=3,试求以折痕EF为边长的正方形面积。8、如图,小颍同学折叠一个直角三角形
的纸片,使A与B重合,折痕为DE,若已知AC=10cm,BC=6cm,你能求出CE的长吗?C7、在等腰△ABC中,AB=AC=13cm ,BC=10cm,求△ABC的面积和AC边上的高。ABCD131310H提示:利用面积相等的关系 练习4、 如图,∠ACB=∠ABD=90°,CA=CB,∠DAB=30°,AD=8,求AC的长。解:∵∠ABD=90°,∠DAB=30°∴BD= AD=4在Rt△ABD中,根据勾股定理在Rt△ABC中,又AD=8 4如图,在△ABC中,AB=AC,D点在CB延长线上,求证:AD2-AB2=BD·CD证明:过A作AE⊥BC于EE∵AB=AC,∴BE=CE在Rt △ADE中,AD2=AE2+DE2在Rt △ABE中,AB2=AE2+BE2∴ AD2-AB2=(AE2+DE2)-(AE2+BE2)= DE2- BE2= (DE+BE)·( DE- BE)= (DE+CE)·( DE- BE)=BD·CD实际问题直角三角
形的问题数学问题利用勾
股定理抽象归类解决建构活动
的线段.11 例2.已知:如图,等边△ABC的边长是 6 .
(1)求高AD的长;
(2)求S△ABC .例题分析36? 已知:如图,等边△ABC的高AD是 .
(1)求边长;
(2)求S△ABC .练一练1046810xEFDCBA8-x8-x10、如图,把长方形纸片ABCD折叠,使顶点A与顶点C重合在一起,EF为折痕。若AB=9,BC=3,试求以折痕EF为边长的正方形面积。8、如图,小颍同学折叠一个直角三角形
的纸片,使A与B重合,折痕为DE,若已知AC=10cm,BC=6cm,你能求出CE的长吗?C7、在等腰△ABC中,AB=AC=13cm ,BC=10cm,求△ABC的面积和AC边上的高。ABCD131310H提示:利用面积相等的关系 练习4、 如图,∠ACB=∠ABD=90°,CA=CB,∠DAB=30°,AD=8,求AC的长。解:∵∠ABD=90°,∠DAB=30°∴BD= AD=4在Rt△ABD中,根据勾股定理在Rt△ABC中,又AD=8 4如图,在△ABC中,AB=AC,D点在CB延长线上,求证:AD2-AB2=BD·CD证明:过A作AE⊥BC于EE∵AB=AC,∴BE=CE在Rt △ADE中,AD2=AE2+DE2在Rt △ABE中,AB2=AE2+BE2∴ AD2-AB2=(AE2+DE2)-(AE2+BE2)= DE2- BE2= (DE+BE)·( DE- BE)= (DE+CE)·( DE- BE)=BD·CD实际问题直角三角
形的问题数学问题利用勾
股定理抽象归类解决建构活动
