2021-2022学年北师大版九年级数学上册6.3反比例函数的应用同步习题(Word版,附答案解析)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学上册6.3反比例函数的应用同步习题(Word版,附答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 445.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-02 11:12:58 | ||
图片预览




文档简介
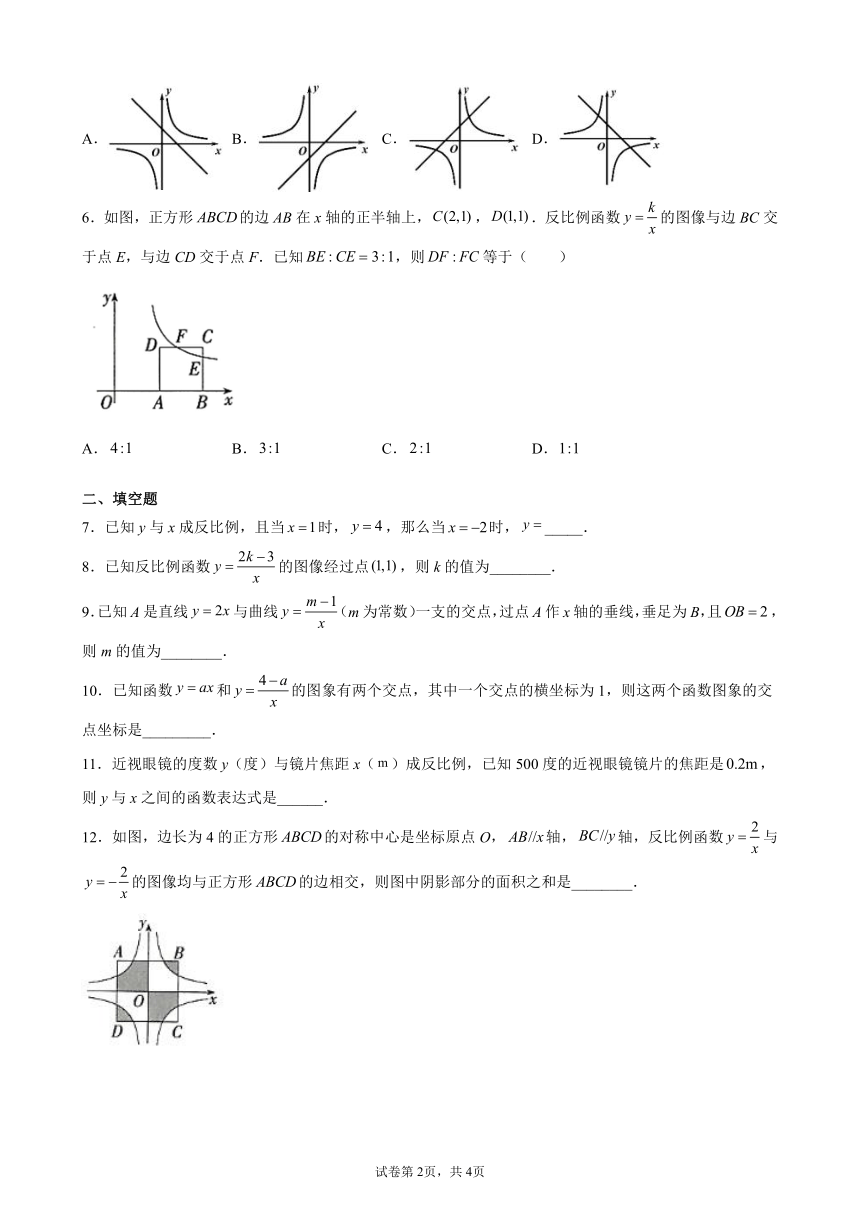
2021-2022学年初中数学九年级上册(北师大版)
6.3反比例函数的应用-同步习题
时间:40分钟
一、单选题
1.已知y与x成反比例函数,且时,,则该函数表达式是( )
A. B. C. D.
2.已知反比例函数,当时,,则( )
A. B. C. D.6
3.已知甲、乙两地相距s(km),汽车从甲地匀速行驶到乙地,则汽车行驶的时间t(h)关于行驶速度v(km/h)的函数图像可能是( )
A. B.
C. D.
4.如果矩形的面积为15cm2,那么它的长ycm与宽xcm之间的函数关系用图象表示大致是( ).
A. B.
C. D.
5.在同一坐标系中,与的图象大致是( )
A. B. C. D.
6.如图,正方形的边AB在x轴的正半轴上,,.反比例函数的图像与边BC交于点E,与边CD交于点F.已知,则等于( )
A. B. C. D.
二、填空题
7.已知y与x成反比例,且当时,,那么当时,_____.
8.已知反比例函数的图像经过点,则k的值为________.
9.已知A是直线与曲线(m为常数)一支的交点,过点A作x轴的垂线,垂足为B,且,则m的值为________.
10.已知函数和的图象有两个交点,其中一个交点的横坐标为1,则这两个函数图象的交点坐标是_________.
11.近视眼镜的度数y(度)与镜片焦距x()成反比例,已知500度的近视眼镜镜片的焦距是,则y与x之间的函数表达式是______.
12.如图,边长为4的正方形的对称中心是坐标原点O,轴,轴,反比例函数与的图像均与正方形的边相交,则图中阴影部分的面积之和是________.
三、解答题
13.如图,是边长为2的等边三角形,若反比例函数的图象过点P,求它的解析式.
14.在同一平面直角坐标系内,画出函数与函数的图象,并利用图象求它们的交点坐标.
15.已知某品牌显示器的寿命大约为.
(1)这种显示器可工作的天数d与平均每日工作的小时数t之间具有怎样的函数关系?
(2)如果平均每天工作,那么这种显示器大约可使用多长时间?
16.某农业大学计划修建一块面积为的矩形试验田.
(1)试验田的长y(单位:m)关于宽x(单位:m)的函数解析式是什么?
(2)如果试验田的长与宽的比为,那么试验田的长与宽分别为多少?
17.如图,直线与轴、轴分别相交于,两点,与双曲线相交于点,轴于点,且,点的坐标为.
(1)求双曲线的解析式;
(2)若点为双曲线上点右侧的一点,且轴于,当以点,,为顶点的三角形与相似时,求点的坐标.
18.已知y与成反比例,并且当时,.
(1)写出y关于x的函数解析式;
(2)当时,求y的值;
(3)当时,求x的值.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.C
【解析】解:设反比例函数表达式为,
∵当x=2时,y= 3,
∴,解得,
∴反比例函数表达式为,
故选C.
2.C
【解析】解:把,代入,得,
解得.
故选:C
3.C
【解析】解:根据题意有:v t=s,
∴,
故t与v之间的函数图象为反比例函数,
且根据实际意义v>0、t>0,
∴其图象在第一象限.
故选:C.
4.C
【解析】解:由矩形的面积公式可得xy=15,
∴y=(x>0,y>0).图象在第一象限.
故选:C.
5.D
【解析】对于一次函数,
当时,,
则直线经过定点,
A、由一次函数的图象得:,由反比例函数的图象得:,两者不一致,此项不符题意;
B、由一次函数的图象得:,由反比例函数的图象得:,两者不一致,此项不符题意;
C、一次函数的图象不经过定点,此项不符题意;
D、由一次函数的图象得:,且经过定点,由反比例函数的图象得:,两者一致,此项符合题意;
故选:D.
6.D
【解析】解:∵四边形为正方形,且,,
∴,,,
∵,
∴,
∴E点坐标为,
把E点坐标代入反比例函数,得,
又∵F点的纵坐标为1,且F点在反比例函数的图像上,
∴F点的横坐标为,
∴,,
∴.
7.-2
【解析】设,
把,代入得
,
解得,
则函数的表达式是,
把代入得.
故答案为-2.
8.2
【解析】解:反比例函数的图象经过点,
将代入得:,
解得:,
故答案为:2.
9.9
【解析】解:由题意,可知OB=2,即点A的横坐标是2或-2,由点A在正比例函数y=2x的图象上,
∴点A的坐标为(2,4)或(-2,-4),
又∵点A在反比例函数y=的图象上,
∴4=或-4=,即m=9.
故答案为:9.
10.(1,2)和(﹣1,﹣2).
【解析】解:把x=1分别代入两个函数中,,,则有a=4﹣a,
解得a=2.
代入原函数得,
解此方程组得和.
所以交点的坐标为(1,2)和(﹣1,﹣2).
故答案为:(1,2)和(﹣1,﹣2).
11.
【解析】解:设,
∵500度的近视眼镜镜片的焦距是,
∴,,
∴y与x之间的函数表达式是:,
故答案为:.
12.8
【解析】解:根据题意:观察图形可得,图中以B、D为顶点的小阴影部分,绕点O顺时针旋转90°,正好和以A、C为顶点的小空白部分重合,所以阴影的面积是图中正方形面积的一半,
且AB∥x轴,BC∥y轴,反比例函数与的图象均与正方形ABCD的边相交,
而边长为4的正方形面积为16,
所以图中的阴影部分的面积是8.
故答案为:8.
13.
【解析】解:过点P作PD⊥x轴于点D,
∵△OPQ是边长为2的等边三角形,
∴OD=OQ=×2=1,
在Rt△OPD中,
∵OP=2,OD=1,
∴PD=,
∴P(1,),
设反比例函数为:y=(k≠0),因为反比例函数的图象过点P,所以k=.
所以所求解析式为:y=.
14.见解析,交点坐标为
【解析】解:图象如图所示:
∴由图象可知函数与函数的交点坐标为.
15.(1);(2)天
【解析】解:(1)∵dt=,d= ;
(2)当t=10时,=,
∴这种显示器大约可使用天.
16.(1);(2),
【解析】解:(1) 由题意得,xy= 2×106,所以y =
∴故试验田的长y(单位:m)关于宽x(单位:m)的函数解析式是y =
(2)设试验田的宽为xm,则长为2xm由题意得,2x·x= 2 ×106,
解得x =±103 (负值舍去),
∴试验田长与宽分别为2 ×103m、103m.
17.(1) (2)或
【解析】解:(1)把代入中,得,
∴,
∵,∴把代入中,
得,
即,
把代入中,
得,
则双曲线解析式为;
(2)如图,轴于点H,连接;设,
∵在双曲线上,
∴,
∵点B在上,
∴.
当时,
可得,即,
∴,即,
解得或(舍去),
∴;
当时,
可得,即,
整理得,
解得或(舍),
∴,
综上所述,或.
18.(1);(2)y=16;(3)x=.
【解析】解:(1)根据题意,设y关于x的函数解析式,
将,代入,得:,
解得:k=36,
∴y关于x的函数解析式为;
(2)当时,;
(3)当y=6时,由得:,解得:.
答案第1页,共2页
答案第1页,共2页
6.3反比例函数的应用-同步习题
时间:40分钟
一、单选题
1.已知y与x成反比例函数,且时,,则该函数表达式是( )
A. B. C. D.
2.已知反比例函数,当时,,则( )
A. B. C. D.6
3.已知甲、乙两地相距s(km),汽车从甲地匀速行驶到乙地,则汽车行驶的时间t(h)关于行驶速度v(km/h)的函数图像可能是( )
A. B.
C. D.
4.如果矩形的面积为15cm2,那么它的长ycm与宽xcm之间的函数关系用图象表示大致是( ).
A. B.
C. D.
5.在同一坐标系中,与的图象大致是( )
A. B. C. D.
6.如图,正方形的边AB在x轴的正半轴上,,.反比例函数的图像与边BC交于点E,与边CD交于点F.已知,则等于( )
A. B. C. D.
二、填空题
7.已知y与x成反比例,且当时,,那么当时,_____.
8.已知反比例函数的图像经过点,则k的值为________.
9.已知A是直线与曲线(m为常数)一支的交点,过点A作x轴的垂线,垂足为B,且,则m的值为________.
10.已知函数和的图象有两个交点,其中一个交点的横坐标为1,则这两个函数图象的交点坐标是_________.
11.近视眼镜的度数y(度)与镜片焦距x()成反比例,已知500度的近视眼镜镜片的焦距是,则y与x之间的函数表达式是______.
12.如图,边长为4的正方形的对称中心是坐标原点O,轴,轴,反比例函数与的图像均与正方形的边相交,则图中阴影部分的面积之和是________.
三、解答题
13.如图,是边长为2的等边三角形,若反比例函数的图象过点P,求它的解析式.
14.在同一平面直角坐标系内,画出函数与函数的图象,并利用图象求它们的交点坐标.
15.已知某品牌显示器的寿命大约为.
(1)这种显示器可工作的天数d与平均每日工作的小时数t之间具有怎样的函数关系?
(2)如果平均每天工作,那么这种显示器大约可使用多长时间?
16.某农业大学计划修建一块面积为的矩形试验田.
(1)试验田的长y(单位:m)关于宽x(单位:m)的函数解析式是什么?
(2)如果试验田的长与宽的比为,那么试验田的长与宽分别为多少?
17.如图,直线与轴、轴分别相交于,两点,与双曲线相交于点,轴于点,且,点的坐标为.
(1)求双曲线的解析式;
(2)若点为双曲线上点右侧的一点,且轴于,当以点,,为顶点的三角形与相似时,求点的坐标.
18.已知y与成反比例,并且当时,.
(1)写出y关于x的函数解析式;
(2)当时,求y的值;
(3)当时,求x的值.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.C
【解析】解:设反比例函数表达式为,
∵当x=2时,y= 3,
∴,解得,
∴反比例函数表达式为,
故选C.
2.C
【解析】解:把,代入,得,
解得.
故选:C
3.C
【解析】解:根据题意有:v t=s,
∴,
故t与v之间的函数图象为反比例函数,
且根据实际意义v>0、t>0,
∴其图象在第一象限.
故选:C.
4.C
【解析】解:由矩形的面积公式可得xy=15,
∴y=(x>0,y>0).图象在第一象限.
故选:C.
5.D
【解析】对于一次函数,
当时,,
则直线经过定点,
A、由一次函数的图象得:,由反比例函数的图象得:,两者不一致,此项不符题意;
B、由一次函数的图象得:,由反比例函数的图象得:,两者不一致,此项不符题意;
C、一次函数的图象不经过定点,此项不符题意;
D、由一次函数的图象得:,且经过定点,由反比例函数的图象得:,两者一致,此项符合题意;
故选:D.
6.D
【解析】解:∵四边形为正方形,且,,
∴,,,
∵,
∴,
∴E点坐标为,
把E点坐标代入反比例函数,得,
又∵F点的纵坐标为1,且F点在反比例函数的图像上,
∴F点的横坐标为,
∴,,
∴.
7.-2
【解析】设,
把,代入得
,
解得,
则函数的表达式是,
把代入得.
故答案为-2.
8.2
【解析】解:反比例函数的图象经过点,
将代入得:,
解得:,
故答案为:2.
9.9
【解析】解:由题意,可知OB=2,即点A的横坐标是2或-2,由点A在正比例函数y=2x的图象上,
∴点A的坐标为(2,4)或(-2,-4),
又∵点A在反比例函数y=的图象上,
∴4=或-4=,即m=9.
故答案为:9.
10.(1,2)和(﹣1,﹣2).
【解析】解:把x=1分别代入两个函数中,,,则有a=4﹣a,
解得a=2.
代入原函数得,
解此方程组得和.
所以交点的坐标为(1,2)和(﹣1,﹣2).
故答案为:(1,2)和(﹣1,﹣2).
11.
【解析】解:设,
∵500度的近视眼镜镜片的焦距是,
∴,,
∴y与x之间的函数表达式是:,
故答案为:.
12.8
【解析】解:根据题意:观察图形可得,图中以B、D为顶点的小阴影部分,绕点O顺时针旋转90°,正好和以A、C为顶点的小空白部分重合,所以阴影的面积是图中正方形面积的一半,
且AB∥x轴,BC∥y轴,反比例函数与的图象均与正方形ABCD的边相交,
而边长为4的正方形面积为16,
所以图中的阴影部分的面积是8.
故答案为:8.
13.
【解析】解:过点P作PD⊥x轴于点D,
∵△OPQ是边长为2的等边三角形,
∴OD=OQ=×2=1,
在Rt△OPD中,
∵OP=2,OD=1,
∴PD=,
∴P(1,),
设反比例函数为:y=(k≠0),因为反比例函数的图象过点P,所以k=.
所以所求解析式为:y=.
14.见解析,交点坐标为
【解析】解:图象如图所示:
∴由图象可知函数与函数的交点坐标为.
15.(1);(2)天
【解析】解:(1)∵dt=,d= ;
(2)当t=10时,=,
∴这种显示器大约可使用天.
16.(1);(2),
【解析】解:(1) 由题意得,xy= 2×106,所以y =
∴故试验田的长y(单位:m)关于宽x(单位:m)的函数解析式是y =
(2)设试验田的宽为xm,则长为2xm由题意得,2x·x= 2 ×106,
解得x =±103 (负值舍去),
∴试验田长与宽分别为2 ×103m、103m.
17.(1) (2)或
【解析】解:(1)把代入中,得,
∴,
∵,∴把代入中,
得,
即,
把代入中,
得,
则双曲线解析式为;
(2)如图,轴于点H,连接;设,
∵在双曲线上,
∴,
∵点B在上,
∴.
当时,
可得,即,
∴,即,
解得或(舍去),
∴;
当时,
可得,即,
整理得,
解得或(舍),
∴,
综上所述,或.
18.(1);(2)y=16;(3)x=.
【解析】解:(1)根据题意,设y关于x的函数解析式,
将,代入,得:,
解得:k=36,
∴y关于x的函数解析式为;
(2)当时,;
(3)当y=6时,由得:,解得:.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
