2021—2022学年人教版九年级数学上册第二十四章圆单元测试(Word版含答案)
文档属性
| 名称 | 2021—2022学年人教版九年级数学上册第二十四章圆单元测试(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 489.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-02 11:46:23 | ||
图片预览

文档简介
2021——2022学年度人教版九年级数学上册 第二十四章 圆 单元测试
一、选择题(30分)
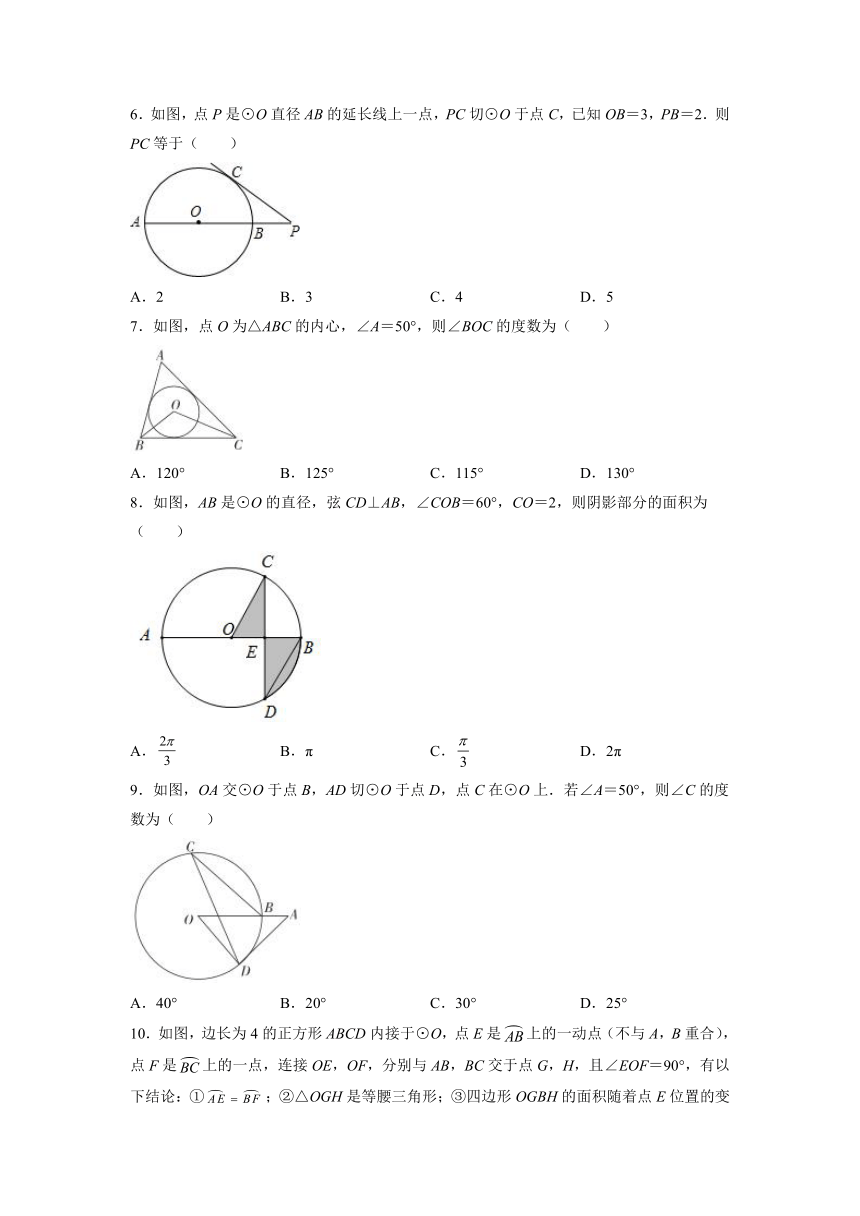
1.如果一个扇形的弧长等于它的半径的倍,那么此扇形称为“优雅扇形”,则半径为2的“优雅扇形”的面积为( )
A.π B. C.π D.2
2.如图,MN为⊙O的弦,∠MON=76°,则∠OMN的度数为( )
A.38° B.52° C.76° D.104°
3.如图,OE⊥AB于E,若⊙O的半径为10,OE=6,则AB为( )
A.8 B.12 C.16 D.6
4.一条排水管的截面如图所示,已知排水管的半径0A=1m,水面宽AB=1.2m,某天下雨后,排水管水面上升了0.2m,则此时排水管水面宽为( )
A.1.4m B.1.6m C.1.8m D.2m
5.如图,△ABC内接于圆O,AC=10,BC=24,且∠A=90°+∠B,则点O到AB的距离为( )
A. B. C.2.4 D.
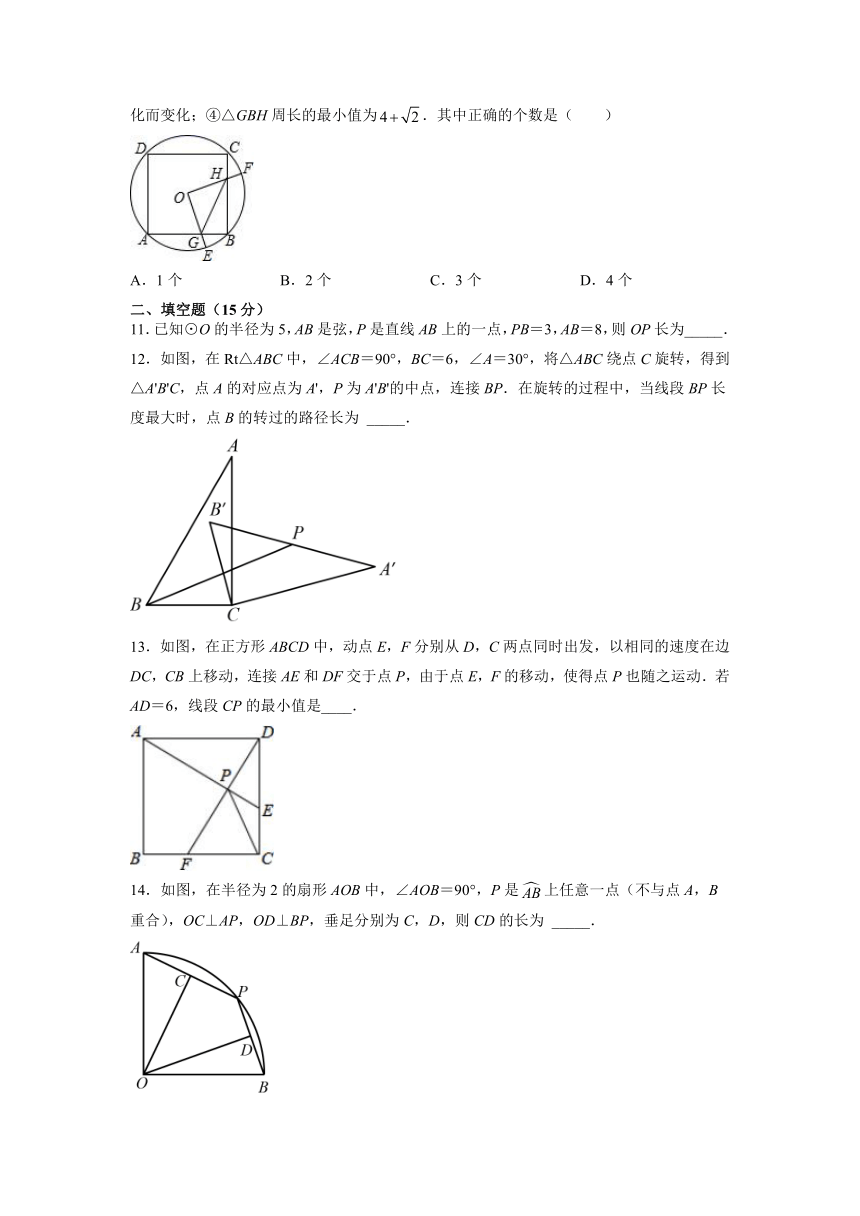
6.如图,点P是⊙O直径AB的延长线上一点,PC切⊙O于点C,已知OB=3,PB=2.则PC等于( )
A.2 B.3 C.4 D.5
7.如图,点O为△ABC的内心,∠A=50°,则∠BOC的度数为( )
A.120° B.125° C.115° D.130°
8.如图,AB是⊙O的直径,弦CD⊥AB,∠COB=60°,CO=2,则阴影部分的面积为( )
A. B.π C. D.2π
9.如图,OA交⊙O于点B,AD切⊙O于点D,点C在⊙O上.若∠A=50°,则∠C的度数为( )
A.40° B.20° C.30° D.25°
10.如图,边长为4的正方形ABCD内接于⊙O,点E是上的一动点(不与A,B重合),点F是上的一点,连接OE,OF,分别与AB,BC交于点G,H,且∠EOF=90°,有以下结论:①;②△OGH是等腰三角形;③四边形OGBH的面积随着点E位置的变化而变化;④△GBH周长的最小值为.其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
二、填空题(15分)
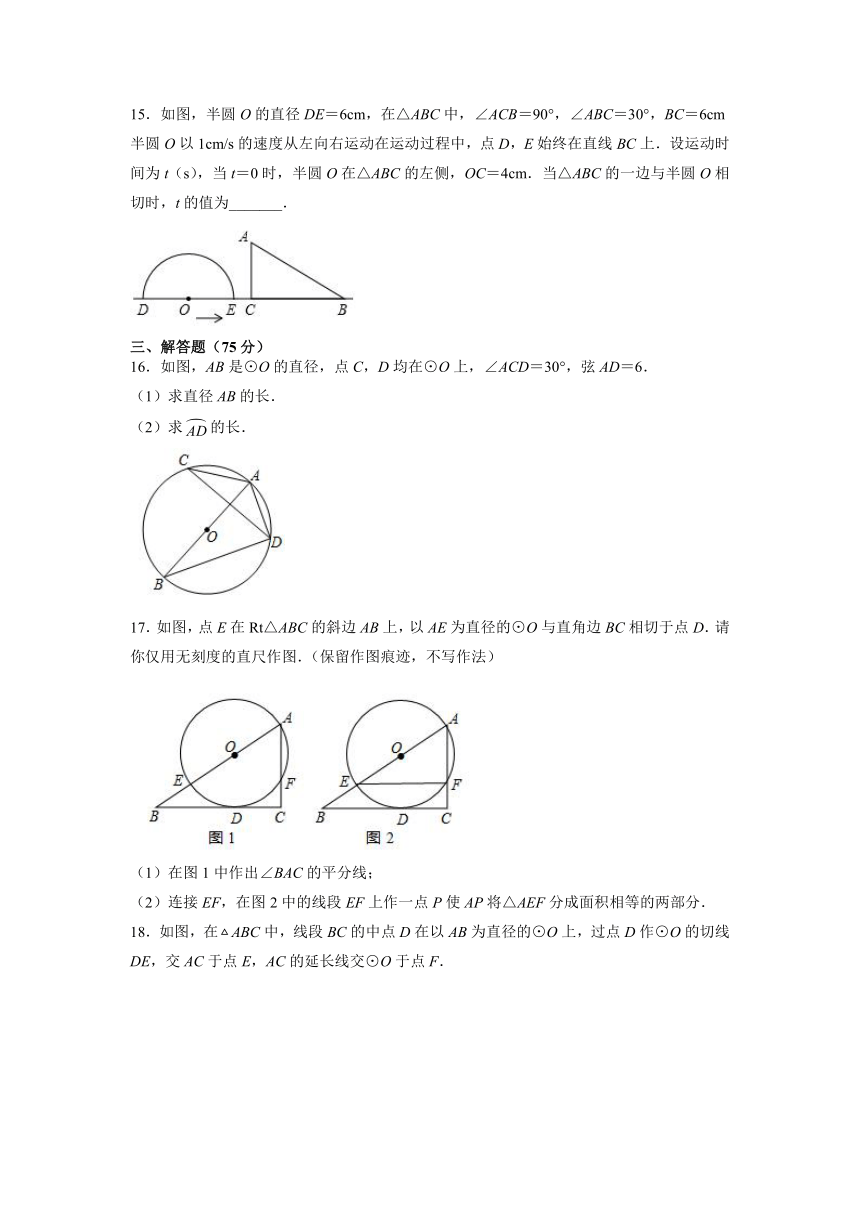
11.已知⊙O的半径为5,AB是弦,P是直线AB上的一点,PB=3,AB=8,则OP长为_____.
12.如图,在Rt△ABC中,∠ACB=90°,BC=6,∠A=30°,将△ABC绕点C旋转,得到△A'B'C,点A的对应点为A',P为A'B'的中点,连接BP.在旋转的过程中,当线段BP长度最大时,点B的转过的路径长为 _____.
13.如图,在正方形ABCD中,动点E,F分别从D,C两点同时出发,以相同的速度在边DC,CB上移动,连接AE和DF交于点P,由于点E,F的移动,使得点P也随之运动.若AD=6,线段CP的最小值是____.
14.如图,在半径为2的扇形AOB中,∠AOB=90°,P是上任意一点(不与点A,B重合),OC⊥AP,OD⊥BP,垂足分别为C,D,则CD的长为 _____.
15.如图,半圆O的直径DE=6cm,在△ABC中,∠ACB=90°,∠ABC=30°,BC=6cm半圆O以1cm/s的速度从左向右运动在运动过程中,点D,E始终在直线BC上.设运动时间为t(s),当t=0时,半圆O在△ABC的左侧,OC=4cm.当△ABC的一边与半圆O相切时,t的值为_______.
三、解答题(75分)
16.如图,AB是⊙O的直径,点C,D均在⊙O上,∠ACD=30°,弦AD=6.
(1)求直径AB的长.
(2)求的长.
17.如图,点E在Rt△ABC的斜边AB上,以AE为直径的⊙O与直角边BC相切于点D.请你仅用无刻度的直尺作图.(保留作图痕迹,不写作法)
(1)在图1中作出∠BAC的平分线;
(2)连接EF,在图2中的线段EF上作一点P使AP将△AEF分成面积相等的两部分.
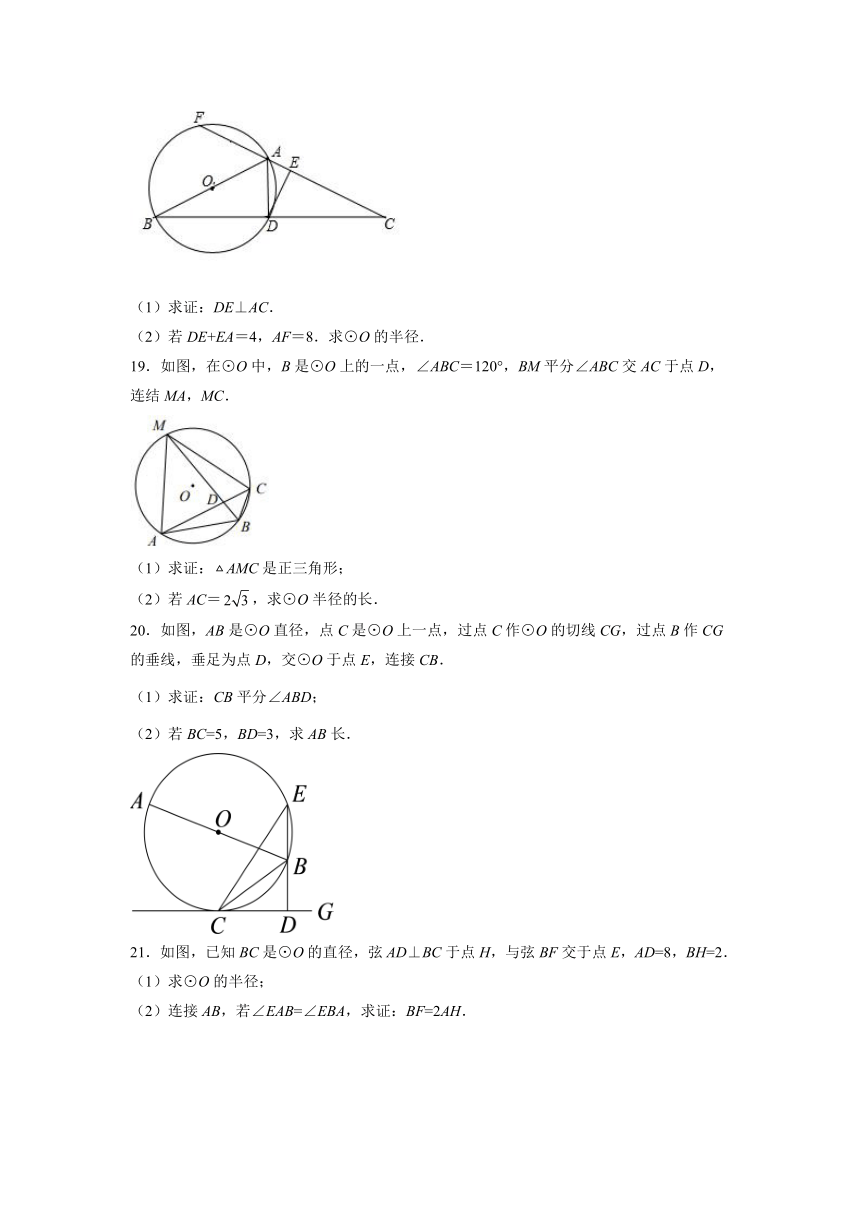
18.如图,在ABC中,线段BC的中点D在以AB为直径的⊙O上,过点D作⊙O的切线DE,交AC于点E,AC的延长线交⊙O于点F.
(1)求证:DE⊥AC.
(2)若DE+EA=4,AF=8.求⊙O的半径.
19.如图,在⊙O中,B是⊙O上的一点,∠ABC=120°,BM平分∠ABC交AC于点D,连结MA,MC.
(1)求证:AMC是正三角形;
(2)若AC=,求⊙O半径的长.
20.如图,AB是⊙O直径,点C是⊙O上一点,过点C作⊙O的切线CG,过点B作CG的垂线,垂足为点D,交⊙O于点E,连接CB.
(1)求证:CB平分∠ABD;
(2)若BC=5,BD=3,求AB长.
21.如图,已知BC是⊙O的直径,弦AD⊥BC于点H,与弦BF交于点E,AD=8,BH=2.
(1)求⊙O的半径;
(2)连接AB,若∠EAB=∠EBA,求证:BF=2AH.
22.如图,AB是⊙O的直径,点D在AB的延长线上,C、E是⊙O上的两点,且CE=CB,∠BCD=∠CAE,延长AE交BC的延长线于点F.
(1)求证:CD是⊙O的切线;
(2)求证:CE=CF;
(3)若AB=2BD=2,求△ABF的面积.
23.如图,与的边相切于点,与边交于点过上一点且是的直径.
(1)求证:是的切线;
(2)若,求的长;
(3)在(2)的条件下,求的长.
【参考答案】
1.D
2.B
3.C
4.B
5.A
6.C
7.C
8.A
9.B
10.B
11.或
12.
13.##
14.
15.1或4或7
16.解:(1),
AB是⊙O的直径,
又AD=6
(2)如图,连接,
又
则是等边三角形
的长为:
17.解:(1)如图1,即为所求;
(2)如图2,即为所求.
18.(1)证明:如图,连接OD,
,
,
∵AB为直径,
∴∠ADB=90°,
∴AD⊥BC,
又∵点D为BC的中点,
∴,
,
,
∴,
是的切线,
,
;
(2)解:如图,过点作于点,
则,
四边形是矩形,
,,
,
设.
,
,,
∵在中,,
,
解得:,
,
的半径为5.
19.(1)证明:∵∠ABC=120°,BM平分∠ABC,
∴∠ABM=∠MBC=∠ABC=60°,
∵∠ABM与∠ACM都是弧AM所对的圆周角,
∴∠ACM=∠ABM=60°,
∵∠MAC与∠MBC都是弧MC所对的圆周角,
∴∠MAC=∠MBC=60°,
∴∠MAC=∠ACM=60°,
∴MA=CM,
又∵∠ACM=60°,
∴AMC是正三角形;
(2)解:连接、,过点作于点,如图1,
,
,
,
∵=,
,
∵,,
,
∵,,
,
设,则,
在中,,
∴,
解得:(舍负),
,
∴的半径为2.
20.(1)连接,如下图:
∵CG是⊙O的切线
∴
根据题意,
∴
∴
∵AB是⊙O直径
∴
∴
∴
∴CB平分∠ABD;
(2)连接,过点作于点,如下图:
∴
∵
∴,
∵,
∴四边形为矩形
∴,
∵,BC=5,BD=3
∴
∴
设,则
∵
∴
∴
∴
∴.
21.(1)解:连接OA,如图,
设⊙O的半径为r,
∵AD⊥OB,
∴AH=DH=4,
在Rt△OHA中,OH=r-2,OA=r,
∴r2=42+(r-2)2,
解得r=5,
即⊙O的半径为5;
(2)∵AD⊥OB,
∴=,AH=DH,
∵∠EAB=∠EBA,
∴=,
∴=,
∴=,
∴BF=AD=2AH.
22.解:(1)证明:如图,连接.
∵是的直径,
∴,
∴
∵,
∴,
∴.
∵,
∴.
∴,
,
∴,
∴,
∴是的切线.
(2)证明:∵,
∴,
∴.
又∵,
∴.
(3)∵,∴,
∴,
∴是斜边上的中线,
∴,
∴.
在中,由勾股定理得.
∴的面积.
23.(1)连接,如图,
是的切线
在与中
,
是半径
是的切线;
(2)连接,
,,
在中,
,
设,则,
在中
解得
(3)连接,,
,
中
,
是的直径.
是直角三角形
一、选择题(30分)
1.如果一个扇形的弧长等于它的半径的倍,那么此扇形称为“优雅扇形”,则半径为2的“优雅扇形”的面积为( )
A.π B. C.π D.2
2.如图,MN为⊙O的弦,∠MON=76°,则∠OMN的度数为( )
A.38° B.52° C.76° D.104°
3.如图,OE⊥AB于E,若⊙O的半径为10,OE=6,则AB为( )
A.8 B.12 C.16 D.6
4.一条排水管的截面如图所示,已知排水管的半径0A=1m,水面宽AB=1.2m,某天下雨后,排水管水面上升了0.2m,则此时排水管水面宽为( )
A.1.4m B.1.6m C.1.8m D.2m
5.如图,△ABC内接于圆O,AC=10,BC=24,且∠A=90°+∠B,则点O到AB的距离为( )
A. B. C.2.4 D.
6.如图,点P是⊙O直径AB的延长线上一点,PC切⊙O于点C,已知OB=3,PB=2.则PC等于( )
A.2 B.3 C.4 D.5
7.如图,点O为△ABC的内心,∠A=50°,则∠BOC的度数为( )
A.120° B.125° C.115° D.130°
8.如图,AB是⊙O的直径,弦CD⊥AB,∠COB=60°,CO=2,则阴影部分的面积为( )
A. B.π C. D.2π
9.如图,OA交⊙O于点B,AD切⊙O于点D,点C在⊙O上.若∠A=50°,则∠C的度数为( )
A.40° B.20° C.30° D.25°
10.如图,边长为4的正方形ABCD内接于⊙O,点E是上的一动点(不与A,B重合),点F是上的一点,连接OE,OF,分别与AB,BC交于点G,H,且∠EOF=90°,有以下结论:①;②△OGH是等腰三角形;③四边形OGBH的面积随着点E位置的变化而变化;④△GBH周长的最小值为.其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
二、填空题(15分)
11.已知⊙O的半径为5,AB是弦,P是直线AB上的一点,PB=3,AB=8,则OP长为_____.
12.如图,在Rt△ABC中,∠ACB=90°,BC=6,∠A=30°,将△ABC绕点C旋转,得到△A'B'C,点A的对应点为A',P为A'B'的中点,连接BP.在旋转的过程中,当线段BP长度最大时,点B的转过的路径长为 _____.
13.如图,在正方形ABCD中,动点E,F分别从D,C两点同时出发,以相同的速度在边DC,CB上移动,连接AE和DF交于点P,由于点E,F的移动,使得点P也随之运动.若AD=6,线段CP的最小值是____.
14.如图,在半径为2的扇形AOB中,∠AOB=90°,P是上任意一点(不与点A,B重合),OC⊥AP,OD⊥BP,垂足分别为C,D,则CD的长为 _____.
15.如图,半圆O的直径DE=6cm,在△ABC中,∠ACB=90°,∠ABC=30°,BC=6cm半圆O以1cm/s的速度从左向右运动在运动过程中,点D,E始终在直线BC上.设运动时间为t(s),当t=0时,半圆O在△ABC的左侧,OC=4cm.当△ABC的一边与半圆O相切时,t的值为_______.
三、解答题(75分)
16.如图,AB是⊙O的直径,点C,D均在⊙O上,∠ACD=30°,弦AD=6.
(1)求直径AB的长.
(2)求的长.
17.如图,点E在Rt△ABC的斜边AB上,以AE为直径的⊙O与直角边BC相切于点D.请你仅用无刻度的直尺作图.(保留作图痕迹,不写作法)
(1)在图1中作出∠BAC的平分线;
(2)连接EF,在图2中的线段EF上作一点P使AP将△AEF分成面积相等的两部分.
18.如图,在ABC中,线段BC的中点D在以AB为直径的⊙O上,过点D作⊙O的切线DE,交AC于点E,AC的延长线交⊙O于点F.
(1)求证:DE⊥AC.
(2)若DE+EA=4,AF=8.求⊙O的半径.
19.如图,在⊙O中,B是⊙O上的一点,∠ABC=120°,BM平分∠ABC交AC于点D,连结MA,MC.
(1)求证:AMC是正三角形;
(2)若AC=,求⊙O半径的长.
20.如图,AB是⊙O直径,点C是⊙O上一点,过点C作⊙O的切线CG,过点B作CG的垂线,垂足为点D,交⊙O于点E,连接CB.
(1)求证:CB平分∠ABD;
(2)若BC=5,BD=3,求AB长.
21.如图,已知BC是⊙O的直径,弦AD⊥BC于点H,与弦BF交于点E,AD=8,BH=2.
(1)求⊙O的半径;
(2)连接AB,若∠EAB=∠EBA,求证:BF=2AH.
22.如图,AB是⊙O的直径,点D在AB的延长线上,C、E是⊙O上的两点,且CE=CB,∠BCD=∠CAE,延长AE交BC的延长线于点F.
(1)求证:CD是⊙O的切线;
(2)求证:CE=CF;
(3)若AB=2BD=2,求△ABF的面积.
23.如图,与的边相切于点,与边交于点过上一点且是的直径.
(1)求证:是的切线;
(2)若,求的长;
(3)在(2)的条件下,求的长.
【参考答案】
1.D
2.B
3.C
4.B
5.A
6.C
7.C
8.A
9.B
10.B
11.或
12.
13.##
14.
15.1或4或7
16.解:(1),
AB是⊙O的直径,
又AD=6
(2)如图,连接,
又
则是等边三角形
的长为:
17.解:(1)如图1,即为所求;
(2)如图2,即为所求.
18.(1)证明:如图,连接OD,
,
,
∵AB为直径,
∴∠ADB=90°,
∴AD⊥BC,
又∵点D为BC的中点,
∴,
,
,
∴,
是的切线,
,
;
(2)解:如图,过点作于点,
则,
四边形是矩形,
,,
,
设.
,
,,
∵在中,,
,
解得:,
,
的半径为5.
19.(1)证明:∵∠ABC=120°,BM平分∠ABC,
∴∠ABM=∠MBC=∠ABC=60°,
∵∠ABM与∠ACM都是弧AM所对的圆周角,
∴∠ACM=∠ABM=60°,
∵∠MAC与∠MBC都是弧MC所对的圆周角,
∴∠MAC=∠MBC=60°,
∴∠MAC=∠ACM=60°,
∴MA=CM,
又∵∠ACM=60°,
∴AMC是正三角形;
(2)解:连接、,过点作于点,如图1,
,
,
,
∵=,
,
∵,,
,
∵,,
,
设,则,
在中,,
∴,
解得:(舍负),
,
∴的半径为2.
20.(1)连接,如下图:
∵CG是⊙O的切线
∴
根据题意,
∴
∴
∵AB是⊙O直径
∴
∴
∴
∴CB平分∠ABD;
(2)连接,过点作于点,如下图:
∴
∵
∴,
∵,
∴四边形为矩形
∴,
∵,BC=5,BD=3
∴
∴
设,则
∵
∴
∴
∴
∴.
21.(1)解:连接OA,如图,
设⊙O的半径为r,
∵AD⊥OB,
∴AH=DH=4,
在Rt△OHA中,OH=r-2,OA=r,
∴r2=42+(r-2)2,
解得r=5,
即⊙O的半径为5;
(2)∵AD⊥OB,
∴=,AH=DH,
∵∠EAB=∠EBA,
∴=,
∴=,
∴=,
∴BF=AD=2AH.
22.解:(1)证明:如图,连接.
∵是的直径,
∴,
∴
∵,
∴,
∴.
∵,
∴.
∴,
,
∴,
∴,
∴是的切线.
(2)证明:∵,
∴,
∴.
又∵,
∴.
(3)∵,∴,
∴,
∴是斜边上的中线,
∴,
∴.
在中,由勾股定理得.
∴的面积.
23.(1)连接,如图,
是的切线
在与中
,
是半径
是的切线;
(2)连接,
,,
在中,
,
设,则,
在中
解得
(3)连接,,
,
中
,
是的直径.
是直角三角形
同课章节目录
