八年级数学(2)勾股定理在几何图形中的计算与应用
文档属性
| 名称 | 八年级数学(2)勾股定理在几何图形中的计算与应用 |

|
|
| 格式 | zip | ||
| 文件大小 | 661.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-02 00:00:00 | ||
图片预览




文档简介
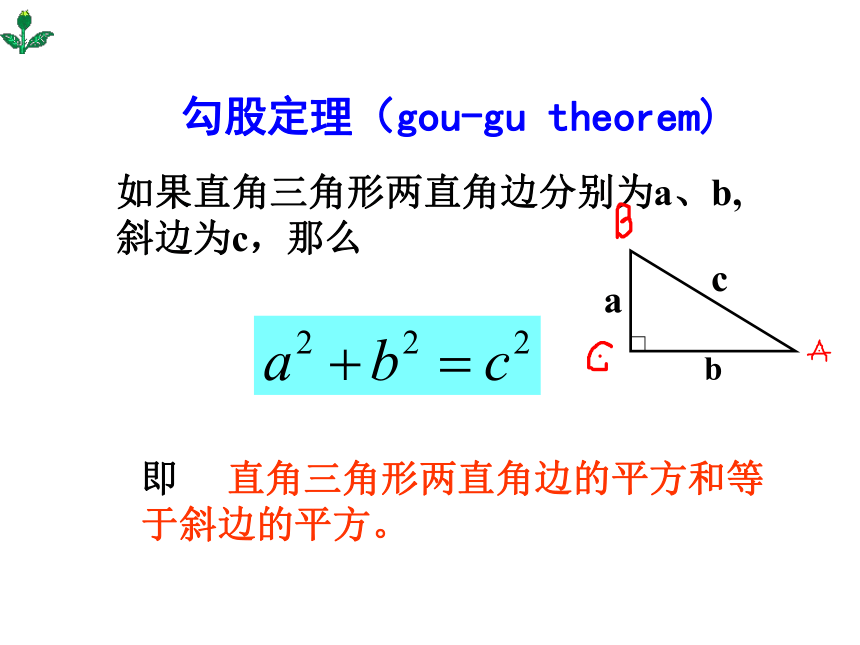
课件43张PPT。勾股定理的应用 勾股定理(gou-gu theorem)如果直角三角形两直角边分别为a、b,斜边为c,那么即 直角三角形两直角边的平方和等于斜边的平方。问题1.直角三角形三边有什么关系?
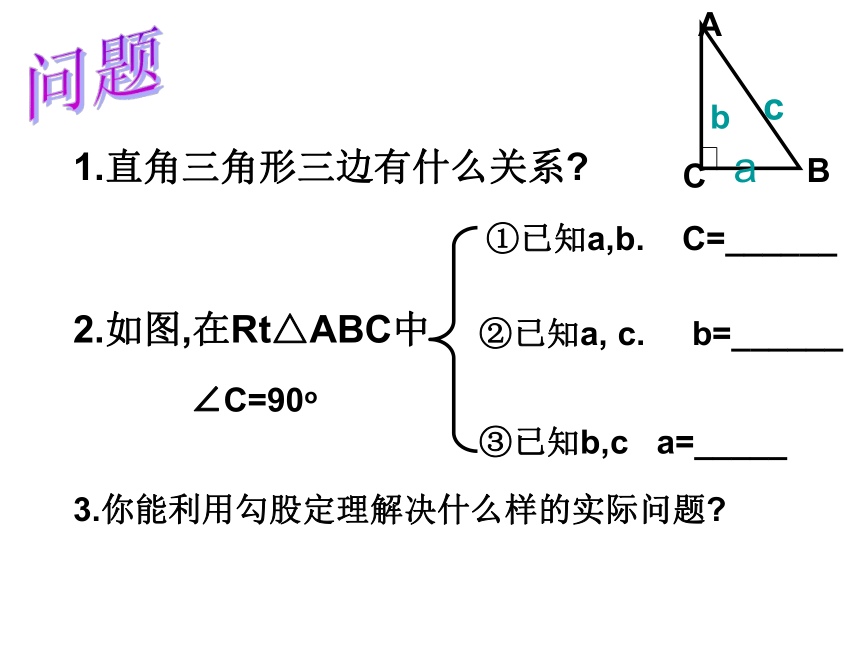
2.如图,在Rt△ABC中
∠C=90o①已知a,b. C=______②已知a, c. b=______③已知b,c a=_____3.你能利用勾股定理解决什么样的实际问题?练习:1、在△ABC中,∠B=90°若a=3,b=5,
则c=
2 、在Rt△ABC中,∠C=90°,∠C的对边为c, c=7,b=3, 则a=_____
3、等腰直角三角形的腰长为3cm,则底边长为 .
4、直角三角形的两边长为3厘米和5厘米,
则第三边长为 .
5、直角三角形两直角边分别为6cm,8cm,
那么这个直角三角形的斜边长为:___ 1、在Rt△ABC中,∠C=90°,
①若a=5,b=12,则c=______;
②若c=61,b=60,则a=_____;
③若a∶b=3∶4,c=10则SRt△ABC=_____。 1311242、把直角三角形两条直角边同时扩大到原来的3倍,则其斜边( )
A.不变 ,
B.扩大到原来的3倍
C.扩大到原来的9倍
D.减小到原来的1/3
B3、已知一个直角三角形的两边长分别为3和4,则第三边长的平方是( )
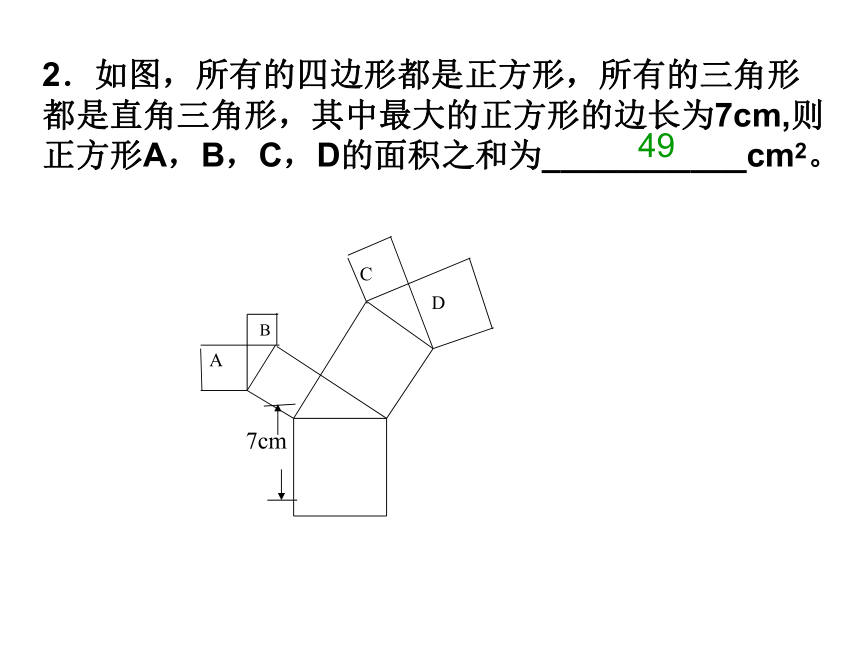
A.25 B.14 C.7 D.7或25ABCD7cm2.如图,所有的四边形都是正方形,所有的三角形
都是直角三角形,其中最大的正方形的边长为7cm,则
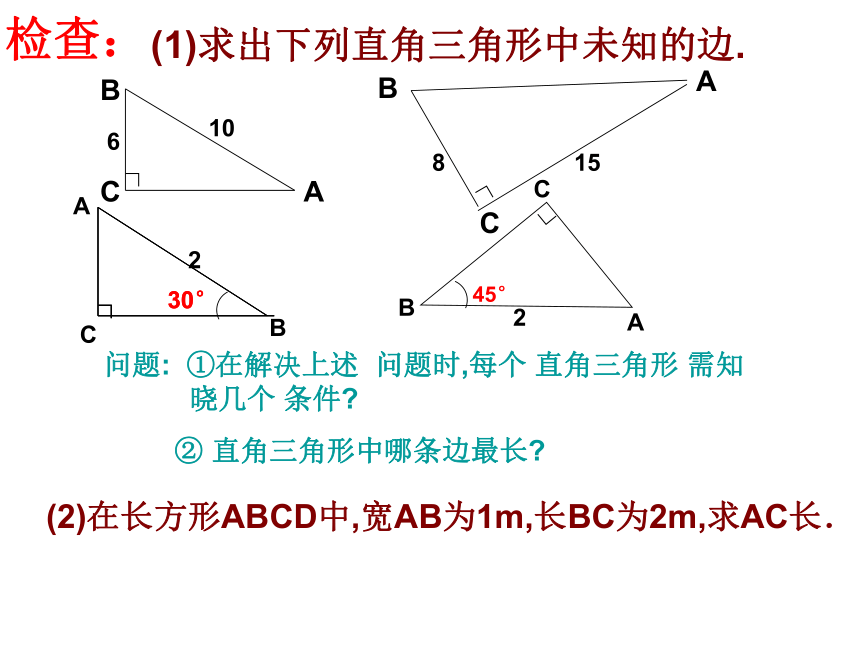
正方形A,B,C,D的面积之和为___________cm2。49(1)求出下列直角三角形中未知的边.问题: ①在解决上述 问题时,每个 直角三角形 需知 晓几个 条件?
② 直角三角形中哪条边最长?
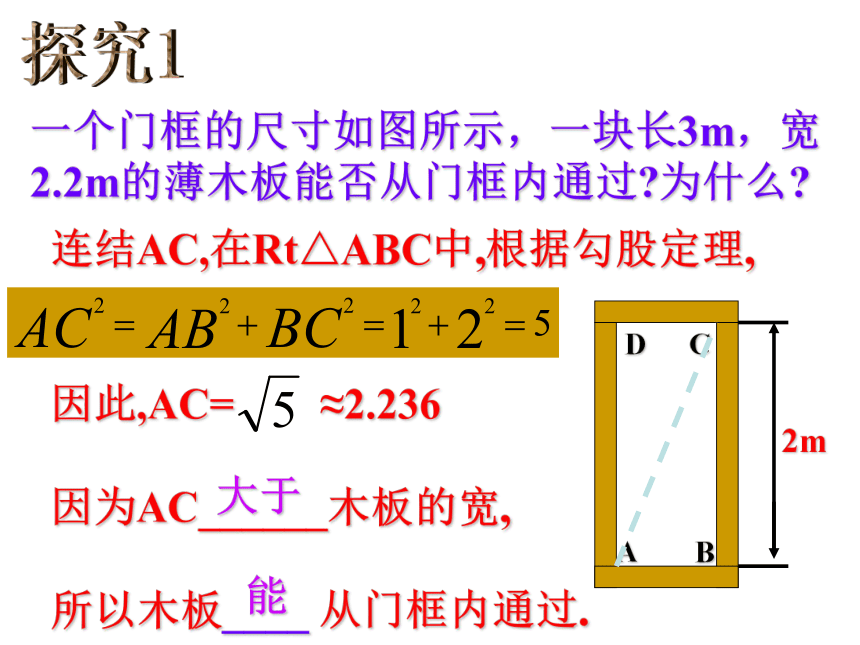
检查:(2)在长方形ABCD中,宽AB为1m,长BC为2m,求AC长. 探究1一个门框的尺寸如图所示,一块长3m,宽2.2m的薄木板能否从门框内通过?为什么?2mDCAB连结AC,在Rt△ABC中,根据勾股定理,
因此,AC= ≈2.236
因为AC______木板的宽,
所以木板____ 从门框内通过.大于能1m2m
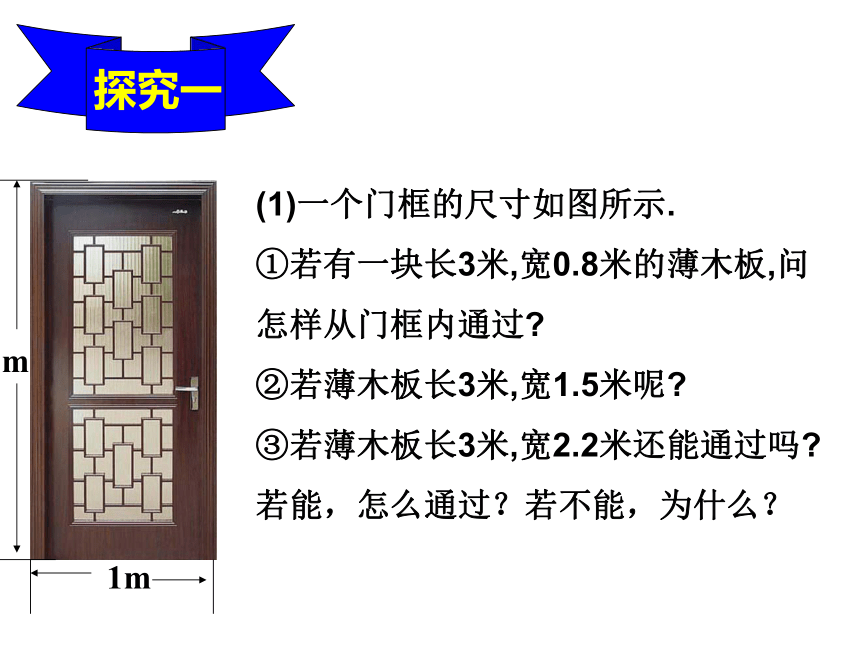
(1)一个门框的尺寸如图所示.
①若有一块长3米,宽0.8米的薄木板,问
怎样从门框内通过?
②若薄木板长3米,宽1.5米呢?
③若薄木板长3米,宽2.2米还能通过吗?
若能,怎么通过?若不能,为什么?
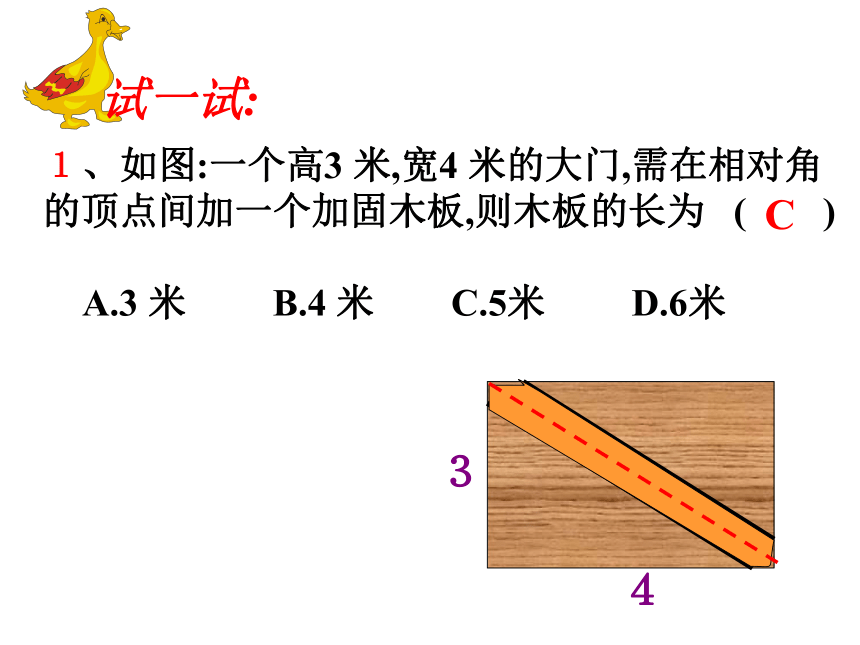
1、如图:一个高3 米,宽4 米的大门,需在相对角的顶点间加一个加固木板,则木板的长为 ( )A.3 米 B.4 米 C.5米 D.6米C试一试:
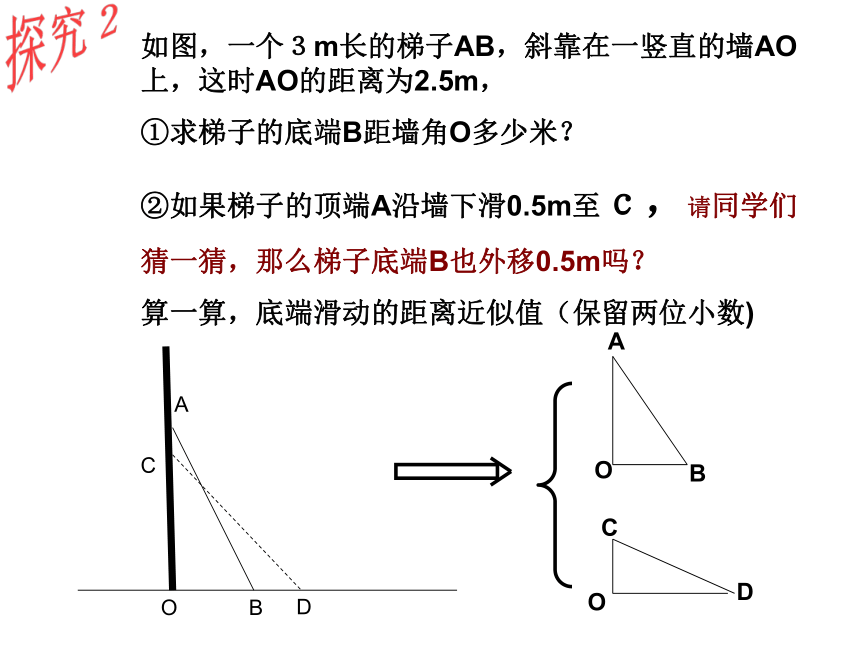
34探究2如图,一个3m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5m,
①求梯子的底端B距墙角O多少米?
②如果梯子的顶端A沿墙下滑0.5m至c,请同学们
猜一猜,那么梯子底端B也外移0.5m吗?
算一算,底端滑动的距离近似值(保留两位小数)在Rt△AOB中oB2=______________oB=______________在Rt△COD中OD2=______________OD=________________BD=_______________梯子的顶端沿墙下滑,梯子底端外移__解AB2-AO2≈1.658mCD2-CO2≈2.236mOD-OB≈0.58m0.58m 2、如图有两颗树,一棵高8m,另一棵高2m,两树相距8m,一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了多少米?8m2m8mABCDE一大楼发生火灾,消防车立即赶到距大楼9米处,升起云梯到失火的窗口,已知发生火灾的窗口距地面有14.2米,云梯底部距地面2.2米,问云梯至少需要搭出多少米可以够到失火的窗口?ABCED帮一帮消防员 DA3、蚂蚁沿图中的折线从A点爬到D点,一共爬了多少厘米?(小方格的边长为1厘米)GFE提示构造直角三角形三、勾股定理的应用 1.已知:直角△ABC中,∠C=90°,
若a=3, b=4, 求 c 的值。(一) 直接运用勾股定理求边若c-a=2, b=6,求 c 的值三、勾股定理的应用 (一) 直接运用勾股定理求边3、若直角三角形的三边长分别为2、 4、 x,则x=_____ .2.已知直角三角形ABC中,
(1)若AC=8,AB=10,则 = ____.
(2) 若 =30,且BC=5,则AB=_____
(3)若 =24,且BC=6,则AB边上的高为_____24134.82、 如图,∠ACB=∠ABD=90°,CA=CB,∠DAB=30°,AD=8,求AC的长。解:∵∠ABD=90°,∠DAB=30°∴BD= AD=4在Rt△ABD中,根据勾股定理在Rt△ABC中,又AD=83.在一棵树的20米的B处有两只猴子,其中一只猴子爬下树走到离树40米的A处,另一只爬到树顶D后直接约向A处,且测得AD为50米,求BD的长.三、勾股定理的应用 (二)先构造,再运用ABC5561、如图,求△ABC的面积D 已知:如图,等边△ABC的高AD是 .
(1)求边长;
(2)求S△ABC .练一练1、在等腰△ABC中,AB=AC=13cm ,BC=10cm,求△ABC的面积和AC边上的高。ABCD131310H提示:利用面积相等的关系 练习勾股定理的应用 校园里有一块三角形空地,现准备在这块空地上种植草皮以美化环境,已经测量出它的三边长分别是13、14、15米,若这种草皮每平方米售价120元,则购买这种草皮至少需要支出多少? 151314Dx14-x勾股定理的应用下图是学校的旗杆,旗杆上的绳子垂到了地面,并多出了一段, 旗杆有多高呢? 你能想个办法吗?请你与同伴交流设计方案? 小明发现旗杆上的绳子垂到地面还多1米,当他们把绳子的下端拉开5米后,发现下端刚好接触地面,你能帮他们把旗杆的高度和绳子的长度计算出来吗? ABC5xx+1如图,小颍同学折叠一个直角三角形的纸片,使A与B重合,折痕为DE,若已知AC=10cm,BC=6cm,你能求出CE的长吗?C解:由题意可知,DE为AB的垂直平分线。连接BE,则AE=BE解得:CE=3.2cm折叠问题 折叠问题2、矩形纸片ABCD中,AD=4cm,AB=10cm,按如图方式折叠,折痕是EF,求DE的长度?ABCDEF(B)(C)1046810xEFDCBA8-x8-x3、在波平如静的湖面上,有一朵美丽的红莲 ,它高出水面1米 ,一阵大风吹过,红莲被吹至一边,花朵齐及水面,如果知道红莲移动的水平距离为2米 ,问这里水深多少?x+1BCAH12?┓xx2+22=(x+1)2试一试: 在我国古代数学著作《九章算术》中记载了一道有趣的问题,这个问题的意思是:有一个水池,水面是一个边长为10尺的正方形,在水池的中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池的深度和这根芦苇的长度各是多少?DABC 无障碍设施建设是社会文明进步的重要标志,是城市管理人性化、现代化的必要举措,是上海成为现代化国际大都市不可或缺的环境条件。2007年在上海举行第12届夏季特殊奥林匹克运动会. 如图,现要在此楼梯旁建造无障碍通道,经测量每格楼梯的高为11.25cm,宽20cm,你能求出通道的长度吗?ACB在Rt△ABC中,∠ACB=90° ∴AB2=AC2+BC2(勾股定理)解:∵AC=11.25×4=45cm,BC=20×3=60cm∴通道的长度为75cm.4560ACB在Rt△ADC中, ∠ADC=30°, ∴AD=2AC=90cm( )解:∵AC=45cm,BC=60cmD若放缓坡度,使∠ADC=30°,则点D还要距离点B多远?30°∴DB=DC-BC= .2007年将在上海举行第12届夏季特殊奥林匹克运动会. 如图,现要在此楼梯旁建造无障碍通道,经测量每格楼梯的高为11.25cm,宽20cm,你能求出通道的长度吗?4560勾股定理的应用 机场入口的铭牌上说明,飞机的行李架是一个56cm×36cm×23cm的长方体空间。一位旅客携带一件长 的画卷,这件画卷能平放入行李架吗? 5636ABCD解:∵四边形ABCD是长方形(已知)∴∠B=90 °(长方形的四个角都是直角)∴在Rt△ABC中, AC2=AB2+BC2(勾股定理)得∵65<66.6,∴长65cm的画卷能放入行李架65cm圆柱(锥)中的最值问题例2、 有一圆形油罐底面圆的周长为24m,高为6m,一只老鼠从距底面1m的A处爬行到对角B处
吃食物,它爬行的最短路线长为多少?AB分析:由于老鼠是沿着圆柱的表面爬行的,故需把圆柱展开成平面图形.根据两点之间线段最短,可以发现A、B分别在圆柱侧面展开图的宽1m处和长24m的中点处,即AB长为最短路线.(如图)聪明的葛藤
葛藤是一种刁钻的植物,它自己腰杆不硬,为了得到阳光的沐浴,常常会选择高大的树木为依托,缠绕其树干盘旋而上。如图(1)所示。
葛藤又是一种聪明的植物,它绕树干攀升的路线,总是沿着最短路径——螺旋线前进的。若将树干的侧面展开成一个平面,如图(2),可清楚的看出葛藤在这个平面上是沿直线上升的。(1)(2)数学奇闻有 一棵树直立在地上,树高2丈,粗3尺,有一根葛藤从树根处缠绕而上,缠绕7周到达树顶,请问这根葛藤条有多长?(1丈等于10尺)ABC20尺3×7=21(尺)聪明的葛藤例4、如图,一只蚂蚁从实心长方体的顶点A出发,沿长方体的表面爬到对角顶点C1处(三条棱长如图所示),问怎样走路线最短?最短路线长为多少?分析: 根据题意分析蚂蚁爬行的路线有三种情况(如图①②③ ),由勾股定理可求得图1中AC1爬行的路线最短.四、长方体中的最值问题思考:如图:正方体的棱长为5cm,一只蚂蚁欲从正方体底面上的顶点A沿正方体的表面到顶点C′处吃食物,那么它需要爬行的最短路程的长是多少?9、如图,是一个三级台阶,它的每一级的长、宽和高分别等于55cm,10cm和6cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物。请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?BA7 .观察下列表格:……请你结合该表格及相关知识,求出b、c的值.
即b= ,c=
8485 如图,Rt△ABE≌Rt△ECD,AB=a,CD=b,AE=c。试证明:
4如图,在△ABC中,AB=AC,D点在CB延长线上,求证:AD2-AB2=BD·CD证明:过A作AE⊥BC于EE∵AB=AC,∴BE=CE在Rt △ADE中,AD2=AE2+DE2在Rt △ABE中,AB2=AE2+BE2∴ AD2-AB2=(AE2+DE2)-(AE2+BE2)= DE2- BE2= (DE+BE)·( DE- BE)= (DE+CE)·( DE- BE)=BD·CD
2.如图,在Rt△ABC中
∠C=90o①已知a,b. C=______②已知a, c. b=______③已知b,c a=_____3.你能利用勾股定理解决什么样的实际问题?练习:1、在△ABC中,∠B=90°若a=3,b=5,
则c=
2 、在Rt△ABC中,∠C=90°,∠C的对边为c, c=7,b=3, 则a=_____
3、等腰直角三角形的腰长为3cm,则底边长为 .
4、直角三角形的两边长为3厘米和5厘米,
则第三边长为 .
5、直角三角形两直角边分别为6cm,8cm,
那么这个直角三角形的斜边长为:___ 1、在Rt△ABC中,∠C=90°,
①若a=5,b=12,则c=______;
②若c=61,b=60,则a=_____;
③若a∶b=3∶4,c=10则SRt△ABC=_____。 1311242、把直角三角形两条直角边同时扩大到原来的3倍,则其斜边( )
A.不变 ,
B.扩大到原来的3倍
C.扩大到原来的9倍
D.减小到原来的1/3
B3、已知一个直角三角形的两边长分别为3和4,则第三边长的平方是( )
A.25 B.14 C.7 D.7或25ABCD7cm2.如图,所有的四边形都是正方形,所有的三角形
都是直角三角形,其中最大的正方形的边长为7cm,则
正方形A,B,C,D的面积之和为___________cm2。49(1)求出下列直角三角形中未知的边.问题: ①在解决上述 问题时,每个 直角三角形 需知 晓几个 条件?
② 直角三角形中哪条边最长?
检查:(2)在长方形ABCD中,宽AB为1m,长BC为2m,求AC长. 探究1一个门框的尺寸如图所示,一块长3m,宽2.2m的薄木板能否从门框内通过?为什么?2mDCAB连结AC,在Rt△ABC中,根据勾股定理,
因此,AC= ≈2.236
因为AC______木板的宽,
所以木板____ 从门框内通过.大于能1m2m
(1)一个门框的尺寸如图所示.
①若有一块长3米,宽0.8米的薄木板,问
怎样从门框内通过?
②若薄木板长3米,宽1.5米呢?
③若薄木板长3米,宽2.2米还能通过吗?
若能,怎么通过?若不能,为什么?
1、如图:一个高3 米,宽4 米的大门,需在相对角的顶点间加一个加固木板,则木板的长为 ( )A.3 米 B.4 米 C.5米 D.6米C试一试:
34探究2如图,一个3m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5m,
①求梯子的底端B距墙角O多少米?
②如果梯子的顶端A沿墙下滑0.5m至c,请同学们
猜一猜,那么梯子底端B也外移0.5m吗?
算一算,底端滑动的距离近似值(保留两位小数)在Rt△AOB中oB2=______________oB=______________在Rt△COD中OD2=______________OD=________________BD=_______________梯子的顶端沿墙下滑,梯子底端外移__解AB2-AO2≈1.658mCD2-CO2≈2.236mOD-OB≈0.58m0.58m 2、如图有两颗树,一棵高8m,另一棵高2m,两树相距8m,一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了多少米?8m2m8mABCDE一大楼发生火灾,消防车立即赶到距大楼9米处,升起云梯到失火的窗口,已知发生火灾的窗口距地面有14.2米,云梯底部距地面2.2米,问云梯至少需要搭出多少米可以够到失火的窗口?ABCED帮一帮消防员 DA3、蚂蚁沿图中的折线从A点爬到D点,一共爬了多少厘米?(小方格的边长为1厘米)GFE提示构造直角三角形三、勾股定理的应用 1.已知:直角△ABC中,∠C=90°,
若a=3, b=4, 求 c 的值。(一) 直接运用勾股定理求边若c-a=2, b=6,求 c 的值三、勾股定理的应用 (一) 直接运用勾股定理求边3、若直角三角形的三边长分别为2、 4、 x,则x=_____ .2.已知直角三角形ABC中,
(1)若AC=8,AB=10,则 = ____.
(2) 若 =30,且BC=5,则AB=_____
(3)若 =24,且BC=6,则AB边上的高为_____24134.82、 如图,∠ACB=∠ABD=90°,CA=CB,∠DAB=30°,AD=8,求AC的长。解:∵∠ABD=90°,∠DAB=30°∴BD= AD=4在Rt△ABD中,根据勾股定理在Rt△ABC中,又AD=83.在一棵树的20米的B处有两只猴子,其中一只猴子爬下树走到离树40米的A处,另一只爬到树顶D后直接约向A处,且测得AD为50米,求BD的长.三、勾股定理的应用 (二)先构造,再运用ABC5561、如图,求△ABC的面积D 已知:如图,等边△ABC的高AD是 .
(1)求边长;
(2)求S△ABC .练一练1、在等腰△ABC中,AB=AC=13cm ,BC=10cm,求△ABC的面积和AC边上的高。ABCD131310H提示:利用面积相等的关系 练习勾股定理的应用 校园里有一块三角形空地,现准备在这块空地上种植草皮以美化环境,已经测量出它的三边长分别是13、14、15米,若这种草皮每平方米售价120元,则购买这种草皮至少需要支出多少? 151314Dx14-x勾股定理的应用下图是学校的旗杆,旗杆上的绳子垂到了地面,并多出了一段, 旗杆有多高呢? 你能想个办法吗?请你与同伴交流设计方案? 小明发现旗杆上的绳子垂到地面还多1米,当他们把绳子的下端拉开5米后,发现下端刚好接触地面,你能帮他们把旗杆的高度和绳子的长度计算出来吗? ABC5xx+1如图,小颍同学折叠一个直角三角形的纸片,使A与B重合,折痕为DE,若已知AC=10cm,BC=6cm,你能求出CE的长吗?C解:由题意可知,DE为AB的垂直平分线。连接BE,则AE=BE解得:CE=3.2cm折叠问题 折叠问题2、矩形纸片ABCD中,AD=4cm,AB=10cm,按如图方式折叠,折痕是EF,求DE的长度?ABCDEF(B)(C)1046810xEFDCBA8-x8-x3、在波平如静的湖面上,有一朵美丽的红莲 ,它高出水面1米 ,一阵大风吹过,红莲被吹至一边,花朵齐及水面,如果知道红莲移动的水平距离为2米 ,问这里水深多少?x+1BCAH12?┓xx2+22=(x+1)2试一试: 在我国古代数学著作《九章算术》中记载了一道有趣的问题,这个问题的意思是:有一个水池,水面是一个边长为10尺的正方形,在水池的中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池的深度和这根芦苇的长度各是多少?DABC 无障碍设施建设是社会文明进步的重要标志,是城市管理人性化、现代化的必要举措,是上海成为现代化国际大都市不可或缺的环境条件。2007年在上海举行第12届夏季特殊奥林匹克运动会. 如图,现要在此楼梯旁建造无障碍通道,经测量每格楼梯的高为11.25cm,宽20cm,你能求出通道的长度吗?ACB在Rt△ABC中,∠ACB=90° ∴AB2=AC2+BC2(勾股定理)解:∵AC=11.25×4=45cm,BC=20×3=60cm∴通道的长度为75cm.4560ACB在Rt△ADC中, ∠ADC=30°, ∴AD=2AC=90cm( )解:∵AC=45cm,BC=60cmD若放缓坡度,使∠ADC=30°,则点D还要距离点B多远?30°∴DB=DC-BC= .2007年将在上海举行第12届夏季特殊奥林匹克运动会. 如图,现要在此楼梯旁建造无障碍通道,经测量每格楼梯的高为11.25cm,宽20cm,你能求出通道的长度吗?4560勾股定理的应用 机场入口的铭牌上说明,飞机的行李架是一个56cm×36cm×23cm的长方体空间。一位旅客携带一件长 的画卷,这件画卷能平放入行李架吗? 5636ABCD解:∵四边形ABCD是长方形(已知)∴∠B=90 °(长方形的四个角都是直角)∴在Rt△ABC中, AC2=AB2+BC2(勾股定理)得∵65<66.6,∴长65cm的画卷能放入行李架65cm圆柱(锥)中的最值问题例2、 有一圆形油罐底面圆的周长为24m,高为6m,一只老鼠从距底面1m的A处爬行到对角B处
吃食物,它爬行的最短路线长为多少?AB分析:由于老鼠是沿着圆柱的表面爬行的,故需把圆柱展开成平面图形.根据两点之间线段最短,可以发现A、B分别在圆柱侧面展开图的宽1m处和长24m的中点处,即AB长为最短路线.(如图)聪明的葛藤
葛藤是一种刁钻的植物,它自己腰杆不硬,为了得到阳光的沐浴,常常会选择高大的树木为依托,缠绕其树干盘旋而上。如图(1)所示。
葛藤又是一种聪明的植物,它绕树干攀升的路线,总是沿着最短路径——螺旋线前进的。若将树干的侧面展开成一个平面,如图(2),可清楚的看出葛藤在这个平面上是沿直线上升的。(1)(2)数学奇闻有 一棵树直立在地上,树高2丈,粗3尺,有一根葛藤从树根处缠绕而上,缠绕7周到达树顶,请问这根葛藤条有多长?(1丈等于10尺)ABC20尺3×7=21(尺)聪明的葛藤例4、如图,一只蚂蚁从实心长方体的顶点A出发,沿长方体的表面爬到对角顶点C1处(三条棱长如图所示),问怎样走路线最短?最短路线长为多少?分析: 根据题意分析蚂蚁爬行的路线有三种情况(如图①②③ ),由勾股定理可求得图1中AC1爬行的路线最短.四、长方体中的最值问题思考:如图:正方体的棱长为5cm,一只蚂蚁欲从正方体底面上的顶点A沿正方体的表面到顶点C′处吃食物,那么它需要爬行的最短路程的长是多少?9、如图,是一个三级台阶,它的每一级的长、宽和高分别等于55cm,10cm和6cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物。请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?BA7 .观察下列表格:……请你结合该表格及相关知识,求出b、c的值.
即b= ,c=
8485 如图,Rt△ABE≌Rt△ECD,AB=a,CD=b,AE=c。试证明:
4如图,在△ABC中,AB=AC,D点在CB延长线上,求证:AD2-AB2=BD·CD证明:过A作AE⊥BC于EE∵AB=AC,∴BE=CE在Rt △ADE中,AD2=AE2+DE2在Rt △ABE中,AB2=AE2+BE2∴ AD2-AB2=(AE2+DE2)-(AE2+BE2)= DE2- BE2= (DE+BE)·( DE- BE)= (DE+CE)·( DE- BE)=BD·CD
