2021-2022学年高一上学期数学人教A版(2019)必修第一册5.3诱导公式课件(19张ppt)
文档属性
| 名称 | 2021-2022学年高一上学期数学人教A版(2019)必修第一册5.3诱导公式课件(19张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-03 15:13:39 | ||
图片预览






文档简介
(共19张PPT)
第五章 三角函数
5.3.1 诱导公式二~六
复习回顾
1三角函数单位圆定义
设任意角c终边与单位圆交点为P(x,y),则
cos d=
tan a
xX
2诱导公式
sin(a+2k n)=sin a,
cos(a+2k T)=cos a,
tan( a+2k)=tan a
1.sin2600+cos2900=1
sinza
tana
cos∠a
3. sin-a=1-cosa
4.对于一切a都有tana.cosa=sina
5.若a是第二象限角则tana
自
1角π+a与a的终边有何位置
关系 你能发现什么数关系
P1(x1,y1)
X
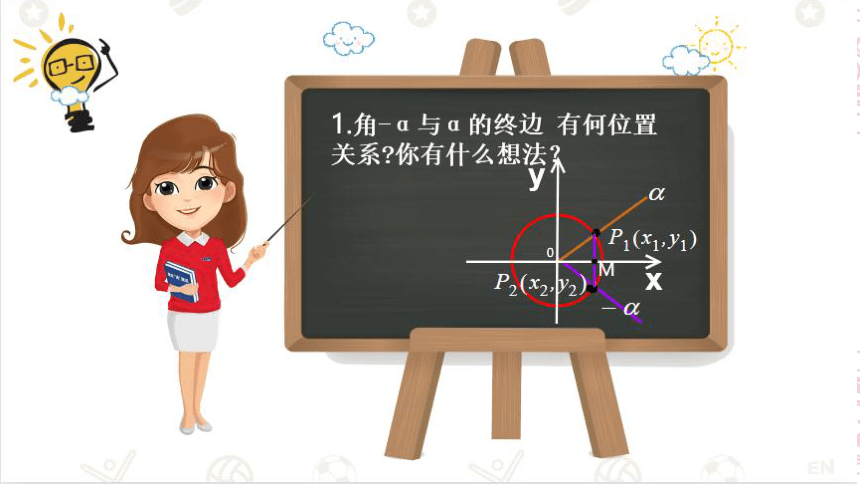
1角-a与a的终边有何位置
关系 你有什么想法
P2(x2p2)
角Ⅱ-a与a的终边有何位置
关系 你能发现什么函数关系
呢
P2(x212)P(x1,y1)
X
思考3:这四个诱导公式有什么规律
a+k.2n(k∈Z,-a,丌±a的三角函数值,等于α的同
名函数值,前面加上一个把α看成锐角时原函数值
的符号
总结为一句话:函数名不变,符号看象限
例1求下列三角函数值
(1)cos225°;(2
(3)sin(6-);(4)tan(-2040°)
通过例题,你对诱导公式
四有什么进一步的认
只 你能归纳任意角的三角函数
化为锐角三角函数的步骤吗
例2.化简
cos(180+a)sin(a+360%)
tan(-a-180°)cos(180°a)
角”-a与a的终边有何位
置关系
P2(x2,y)
x1.y
1角2+a与a的终边有何位
置关系
P2(x2y2)
诱导公式可统一为
角函数与a的三角函数之间的
关系,你有什么办法记住这些
式
:奇变偶
符号看象限
诀的意义
k.±a(k∈Z)的三角函数值
当k为偶数时,等于a的同名三角函数值,前面加上
个把α看作锐角时原三角函数值的符号
2)当为奇数时,等于c的异名三角函数值,前面加上
个把α看作锐角时原三角函数值的符
3.证明
丌
(1).sin( -a)=-cos a; (2 )cos(
slnc。
sin (2Tt-acosTt+acos-+acOS
2
例4化简
sin (3r-asin(-r-asin/2
例5已知sin(53-a)
且-270
5
求sin(37+a)的值
总结
当本节课你学会了什么
(公式二)sin(+a)=-sina,(公式三)sin(-a)=-sina
k·2丌)
诱导公式
-cos d
cos(-a)
Cos C
cos(a+k 2)=cos
其中,k∈z
tan(-a)
(公式三)sin(-a)
sin(--a)=cos a
sin(-+a)
公式五
公式六
s-a)=sin a
cO
口诀:奇变偶不变理符号看象限
E: E:::
目
A
第五章 三角函数
5.3.1 诱导公式二~六
复习回顾
1三角函数单位圆定义
设任意角c终边与单位圆交点为P(x,y),则
cos d=
tan a
xX
2诱导公式
sin(a+2k n)=sin a,
cos(a+2k T)=cos a,
tan( a+2k)=tan a
1.sin2600+cos2900=1
sinza
tana
cos∠a
3. sin-a=1-cosa
4.对于一切a都有tana.cosa=sina
5.若a是第二象限角则tana
自
1角π+a与a的终边有何位置
关系 你能发现什么数关系
P1(x1,y1)
X
1角-a与a的终边有何位置
关系 你有什么想法
P2(x2p2)
角Ⅱ-a与a的终边有何位置
关系 你能发现什么函数关系
呢
P2(x212)P(x1,y1)
X
思考3:这四个诱导公式有什么规律
a+k.2n(k∈Z,-a,丌±a的三角函数值,等于α的同
名函数值,前面加上一个把α看成锐角时原函数值
的符号
总结为一句话:函数名不变,符号看象限
例1求下列三角函数值
(1)cos225°;(2
(3)sin(6-);(4)tan(-2040°)
通过例题,你对诱导公式
四有什么进一步的认
只 你能归纳任意角的三角函数
化为锐角三角函数的步骤吗
例2.化简
cos(180+a)sin(a+360%)
tan(-a-180°)cos(180°a)
角”-a与a的终边有何位
置关系
P2(x2,y)
x1.y
1角2+a与a的终边有何位
置关系
P2(x2y2)
诱导公式可统一为
角函数与a的三角函数之间的
关系,你有什么办法记住这些
式
:奇变偶
符号看象限
诀的意义
k.±a(k∈Z)的三角函数值
当k为偶数时,等于a的同名三角函数值,前面加上
个把α看作锐角时原三角函数值的符号
2)当为奇数时,等于c的异名三角函数值,前面加上
个把α看作锐角时原三角函数值的符
3.证明
丌
(1).sin( -a)=-cos a; (2 )cos(
slnc。
sin (2Tt-acosTt+acos-+acOS
2
例4化简
sin (3r-asin(-r-asin/2
例5已知sin(53-a)
且-270
5
求sin(37+a)的值
总结
当本节课你学会了什么
(公式二)sin(+a)=-sina,(公式三)sin(-a)=-sina
k·2丌)
诱导公式
-cos d
cos(-a)
Cos C
cos(a+k 2)=cos
其中,k∈z
tan(-a)
(公式三)sin(-a)
sin(--a)=cos a
sin(-+a)
公式五
公式六
s-a)=sin a
cO
口诀:奇变偶不变理符号看象限
E: E:::
目
A
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
